Практика 8 Алгоритм SVM. Точность. Оператор эрозии и

Данные для занятия
Презентация

Наивный расчет SVM

Среди всех векторов выберем такие два, которые характеризуют всю выборку. Их будем называть опорными

$$x^{(1)} = [2, 3] \quad \text{с меткой} \quad y^{(1)} = -1$$

$$x^{(2)} = [6, -1] \quad \text{с меткой} \quad y^{(2)} = 1$$

Для жесткой SVM (без ошибок) оптимальное решение должно удовлетворять условиям равенства для опорных векторов:

$$y^{(i)} (w^T x^{(i)} + b) = 1 \quad \text{для} \quad i = 1, 2.$$

То есть получаем систему уравнений:

Для $i = 1$:

$$-1 \cdot (w^T [2, 3] + b) = 1 \quad \Rightarrow \quad w^T [2, 3] + b = -1.$$

Для $i = 2$:

$$1 \cdot (w^T [6, -1] + b) = 1 \quad \Rightarrow \quad w^T [6, -1] + b = 1.$$

Обозначим $w = [w_1, w_2]$. Тогда у нас получается:

$$2w_1 + 3w_2 + b = -1 \quad (1)$$

$$6w_1 - w_2 + b = 1 \quad (2)$$

Нахождение $w$ и $b$:

Вычтем (1) из (2), чтобы исключить $b$:

$$(6w_1 - w_2 + b) - (2w_1 + 3w_2 + b) = 1 - (-1)$$

$$6w_1 - w_2 - 2w_1 - 3w_2 = 2$$

$$4w_1 - 4w_2 = 2 \quad \Rightarrow \quad w_1 - w_2 = 0.5.$$

Отсюда:

$$w_1 = w_2 + 0.5.$$

Теперь подставим это в одно из уравнений, например, в (2):

$$6(w_2 + 0.5) - w_2 + b = 1$$

$$6w_2 + 3 - w_2 + b = 1 \quad \Rightarrow \quad 5w_2 + b = -2.$$

Отсюда:

$$b = -2 - 5w_2.$$

Обратите внимание, что в задаче SVM масштаб параметров не уникален (решение определяется до умножения на положительную константу). Оптимальное решение выбирается как то, у которого $\|w\|$ минимально. При двух точках оптимальная гиперплоскость должна быть перпендикулярна вектору, соединяющему $x^{(1)}$ и $x^{(2)}$.

Найдем вектор, соединяющий $x^{(1)}$ и $x^{(2)}$:

$$x^{(2)} - x^{(1)} = [6 - 2, -1 - 3] = [4, -4].$$

Таким образом, нормаль к гиперплоскости должна быть параллельна $[4, -4]$ (или пропорциональна $[1, -1]$). Это означает, что можно выбрать:

$$w = c [1, -1].$$

Чтобы удовлетворить условию $w_1 = w_2 + 0.5$, подставим $w_1 = c$ и $w_2 = -c$:

$$c = (-c) + 0.5 \quad \Rightarrow \quad 2c = 0.5 \quad \Rightarrow \quad c = 0.25.$$

Таким образом, оптимальное решение (после выбора масштаба) имеет:

$$w = [0.25, -0.25].$$

Теперь найдём $b$ с использованием любого уравнения, например, уравнения (1):

$$2(0.25) + 3(-0.25) + b = -1$$

$$0.5 - 0.75 + b = -1 \quad \Rightarrow \quad b = -1 + 0.25 = -0.75.$$

Проверка:

Для $x^{(1)} = [2, 3]$ с $y^{(1)} = -1$:

$$w^T x^{(1)} + b = 0.25 \cdot 2 + (-0.25) \cdot 3 - 0.75 = 0.5 - 0.75 - 0.75 = -1.0.$$

Умножая на $y^{(1)} = -1$, получаем:

$$-1 \cdot (-1.0) = 1.$$

Для $x^{(2)} = [6, -1]$ с $y^{(2)} = 1$:

$$w^T x^{(2)} + b = 0.25 \cdot 6 + (-0.25) \cdot (-1) - 0.75 = 1.5 + 0.25 - 0.75 = 1.0.$$

Умножая на $y^{(2)} = 1$, получаем:

$$1 \cdot 1.0 = 1.$$

Таким образом, оба условия равенства выполняются.

Ответ:

$$w = (0.25, -0.25), \quad b = -0.75.$$

Эта пара $(w, b)$ задаёт оптимальную гиперплоскость SVM, которая разделяет два класса с максимальным отступом.

Сведение к общим формулам

Пусть заданы вещественные числа $a_1, \dots, a_n, b$, причем не все $\{a_j\}_{j=1}^{n}$ равны нулю. Уравнение
$$w_1 x_1 + w_2 x_2 + \dots + w_n x_n = b$$
относительно переменных $x_1, x_2, \dots, x_n$ задает в $\mathbb{R}^n$ множество, называемое гиперплоскостью (в частном случае гиперплоскости в $\mathbb{R}^2$ она, очевидно, является прямой).

Если в пространстве $\mathbb{R}^n$ скалярное произведение векторов
$$X := (x_1, \dots, x_n) \quad \text{и} \quad Y := (y_1, \dots, y_n)$$
задается стандартным способом
$$\langle X, Y \rangle = x_1 y_1 + \dots + x_n y_n,$$
то уравнение гиперплоскости можно переписать в виде
$$\langle X, W \rangle = b$$
при
$$W := (w_1, \dots, w_n).$$
В этом случае вектор $W$ интерпретируется как вектор нормали к гиперплоскости. Действительно, если $X_1$ и $X_2$ — две точки, лежащие на гиперплоскости, то вектор $W$ перпендикулярен вектору $\overrightarrow{X_1 X_2}$:
$$\langle X_1, W \rangle = b, \quad \langle X_2, W \rangle = b \Rightarrow \langle X_2 - X_1, W \rangle = 0.$$

Каждая гиперплоскость делит $\mathbb{R}^n$ на два подмножества. Для точек одного из них выполняется неравенство
$$w_1 x_1 + w_2 x_2 + \dots + w_n x_n > b,$$
а для точек другого —
$$w_1 x_1 + w_2 x_2 + \dots + w_n x_n < b.$$
Каждое из этих множеств называется (открытым) полупространством, определяемым данной гиперплоскостью. Если к полупространству присоединяются точки гиперплоскости, то получившееся множество называется замкнутым полупространством.

Теорема. Если точка $X_0$ лежит в гиперплоскости
$$\langle X, W \rangle = b,$$
то точка $X_0 + tW$ при любом положительном значении параметра $t$ лежит в полупространстве
$$\langle X, W \rangle > b.$$

Доказательство.
$$\langle X_0, W \rangle = b \Rightarrow \langle X_0 + tW, W \rangle = \langle X_0, W \rangle + t \langle W, W \rangle = b + t \langle W, W \rangle > b$$
при $t > 0$.

Теорема. Для различных точек $X_1$ и $X_2$ оптимальная разделяющая гиперплоскость задается уравнением
$$\langle X - X_c, X_1 - X_2 \rangle = 0,$$
где
$$X_c := \frac{1}{2}(X_1 + X_2).$$
Расстояние от нее до любой из точек $X_1$ и $X_2$ равно
$$\frac{1}{2} \| X_1 - X_2 \|.$$

Доказательство.
Точка $X_c$ определяет середину отрезка $[X_1, X_2]$. Все разделяющие гиперплоскости, которые равноудалены от точек $X_1$ и $X_2$, должны содержать точку $X_c$. Уравнение любой такой гиперплоскости можно представить в виде
$$\langle X - X_c, A \rangle = 0$$
при некотором векторе $W$ единичной длины:
$$|W| := \sqrt{w_1^2 + \dots + w_n^2} = 1.$$
Расстояние от точки $X_1$ до этой гиперплоскости равно
$$\left| \langle X_1 - X_c, W \rangle \right| = \left| \langle X_2 - X_c, W \rangle \right|,$$
причем числа под модулями имеют разные знаки. Пусть, для определенности,
$$\langle X_1 - X_c, W \rangle > 0.$$
Мы хотим вычислить
$$\max \langle X_1 - X_c, W \rangle > 0 \quad \text{при} \quad W \in \mathbb{R}^n, \, |W| = 1.$$
Решаем эту задачу условной оптимизации методом множителей Лагранжа. Вводим множитель Лагранжа $\lambda$ и разыскиваем стационарные точки полинома
$$L(w_1, \dots, w_n; \lambda) := \langle X_1 - X_c, W \rangle - \lambda \langle W, W \rangle = \langle X_1 - X_c, W \rangle - \lambda (w_1^2 + \dots + w_n^2 - 1).$$
Они определяются из системы уравнений
$$\frac{\partial L}{\partial w_1} = 0, \quad \dots, \quad \frac{\partial L}{\partial w_n} = 0, \quad \frac{\partial L}{\partial \lambda} = 0,$$
которую можно переписать в векторном виде
$$X_1 - X_c = 2 \lambda W, \quad \langle W, W \rangle = 1.$$
Первое из этих уравнений означает, что вектор нормали $W$ к искомой плоскости должен быть коллинеарен вектору $X_1 - X_c$, а фактически, вектору $X_1 - X_2 = \overrightarrow{X_2 X_1}$. Таким образом, мы знаем точку на гиперплосте

Продолжение работы

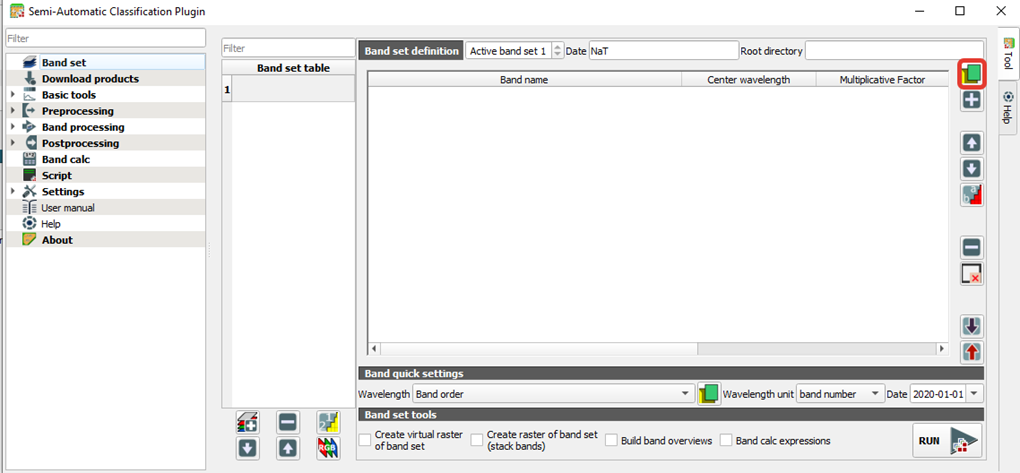
Для продолжения работы оставьте только следующие классы:
- Городская застройка
- Гари
- Поля распаханные
- Поля (зеленые)
- Вода

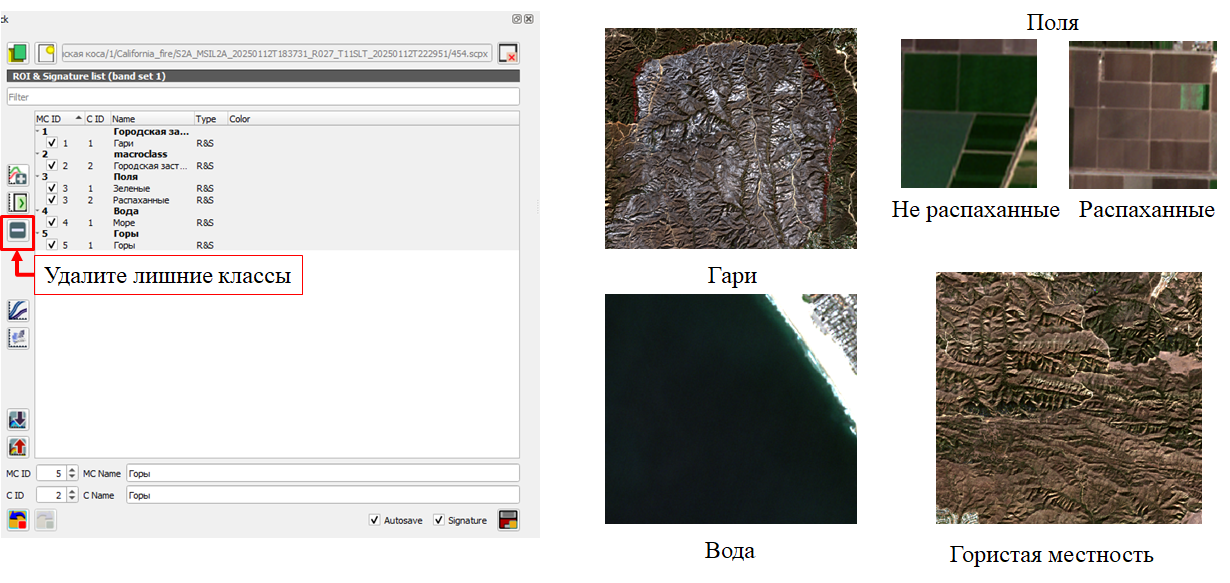
Примерное распредление сигнатур должно быть следующим:

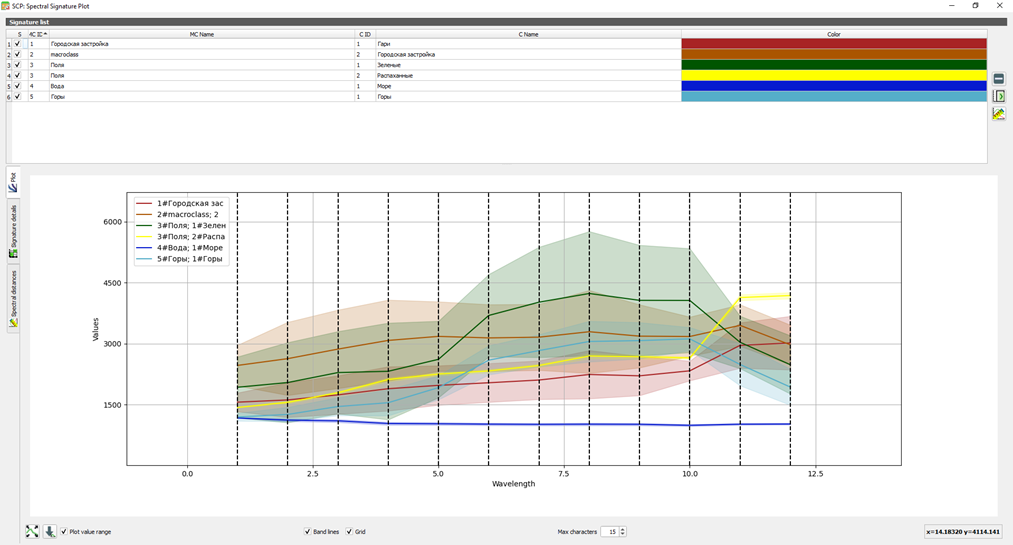
!! note
Спектральная сигнатура, то есть уникальная зависимость отражательной способности материалов от длины волны электромагнитного излучения.

Во вкладке signature details вы можете увидеть информацию о выборке по каждой сигнатуре (сколько пикселей в выборке, какое среднее значение по каналам и по классам)

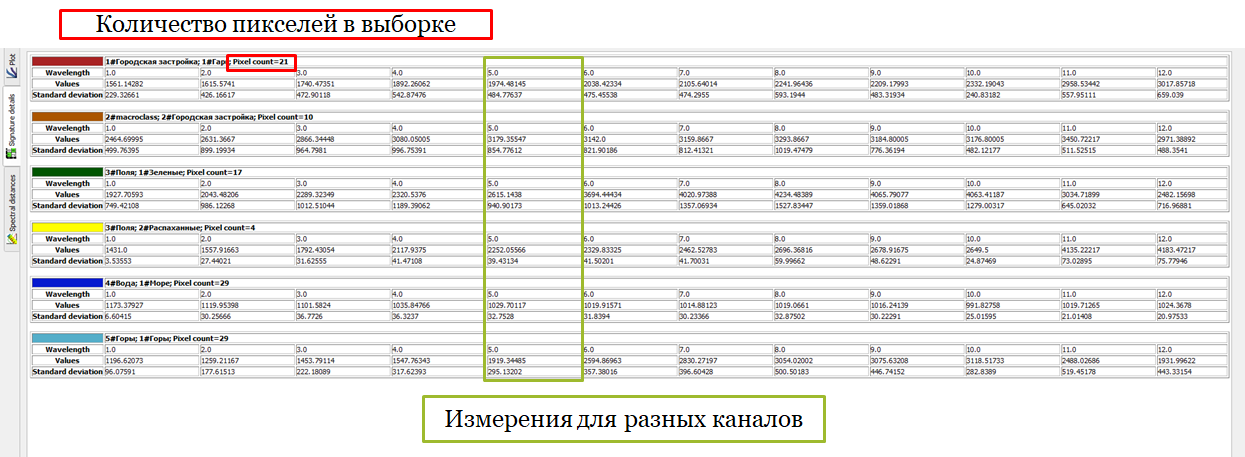
Классифицируйте растр используя алгоритм SVM (Вкладка SCP -> Band -> Band processing -> сlassification)

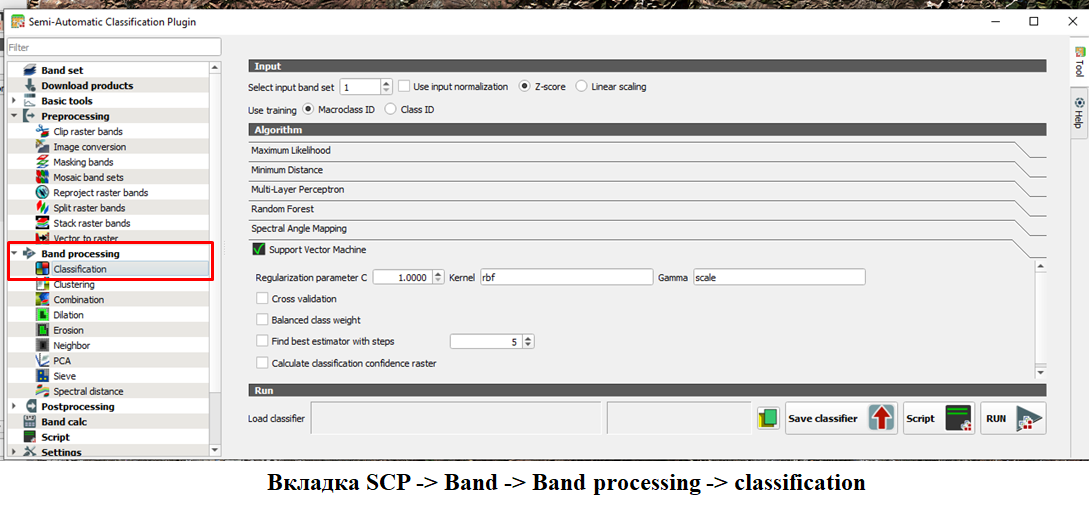
Не забудьте сохранить перед расчетом!

Точность классификации

Оценка точности — важный шаг после классификации земель, который помогает выявить ошибки, проверить каждый класс и в целом оценить надёжность карты.

В SCP существует два инструмента оценки точности сlassification report(отчет о классификации) и accuracy(точность)

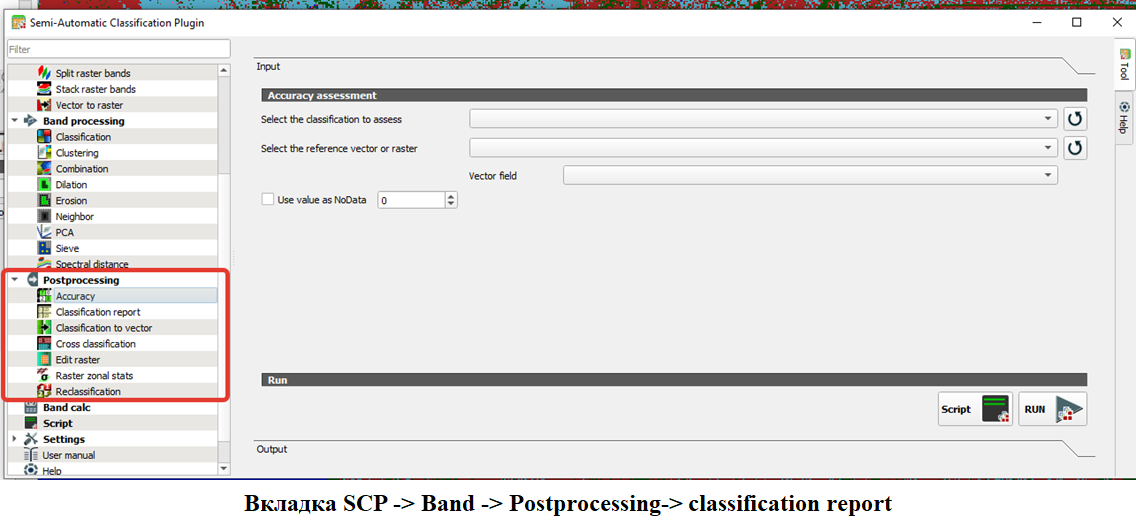
Инструмент Classification report предоставляет описательную статистику классификации, позволяя проанализировать распределение классов и их долю в общей картине. Он доступен во вкладке Postprocessing.

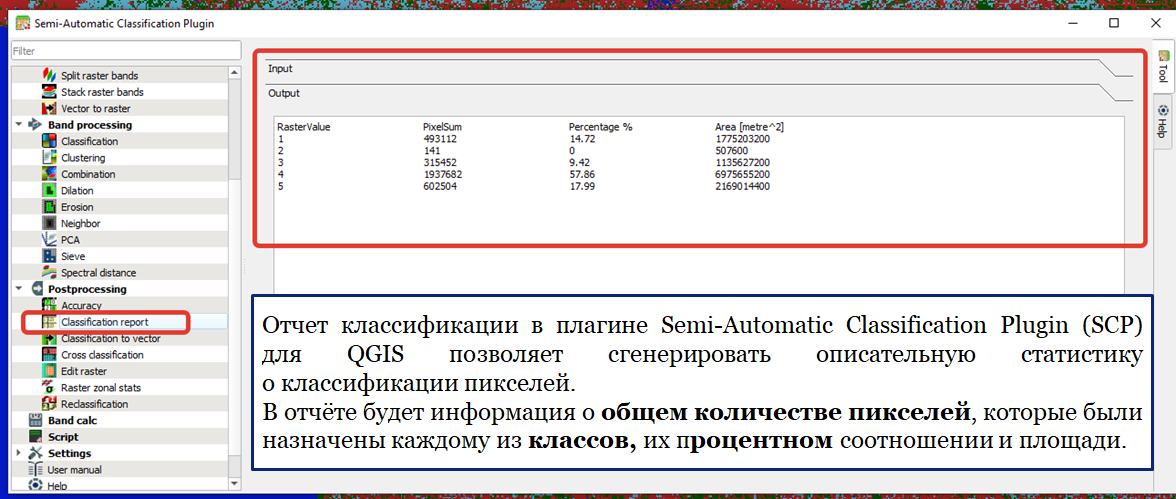
• Подсчёт количества пикселей для каждого класса.
• Вычисление относительного процента покрытия каждым классом.
• Площадь каждого класса в итоговом изображении

Инструмент Accuracy предназначен для детальной оценки точности классификации с использованием референсных(эталонных) данных. Он позволяет рассчитать матрицу ошибок (confusion matrix), которая показывает, насколько точно каждый класс был определён.

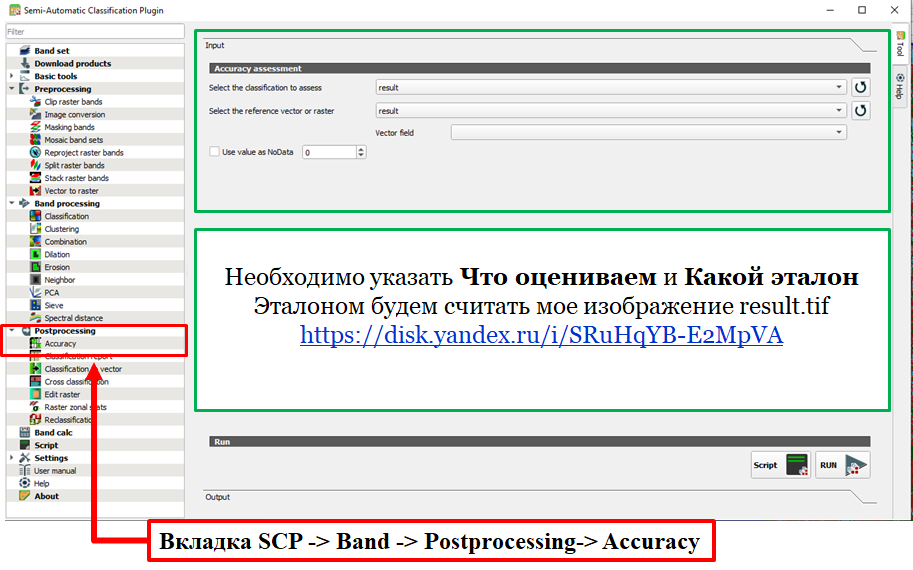
Шаги для оценки точности

1. Добавить классифицированные изображения в интерфейс QGIS.
2. Открыть окно SCP Band Set, выбрав «SCP» > «Постобработка» > «Точность» из главного меню.
3. В открывшемся окне оценки точности:
4. Выбрать классификацию для оценки (растр классификации).
5. Обновить список.
6. Выбрать референсный вектор или растр (слой, используемый для оценки точности), затем обновить список.
7. Если выбран векторный слой, указать поле, содержащее числовые значения классов.
8. Проверить опцию «Использовать значение как NoData» (при включении пиксели с NoData исключаются из расчёта).
9. Нажать «Выполнить», выбрать место сохранения и начать расчёт.

В результате создаётся:
- Файл с ошибками в формате .tif, где значения пикселей представляют категории сравнения между классификацией и референсом.
- Текстовый файл с матрицей ошибок, содержащий количественные показатели точности.

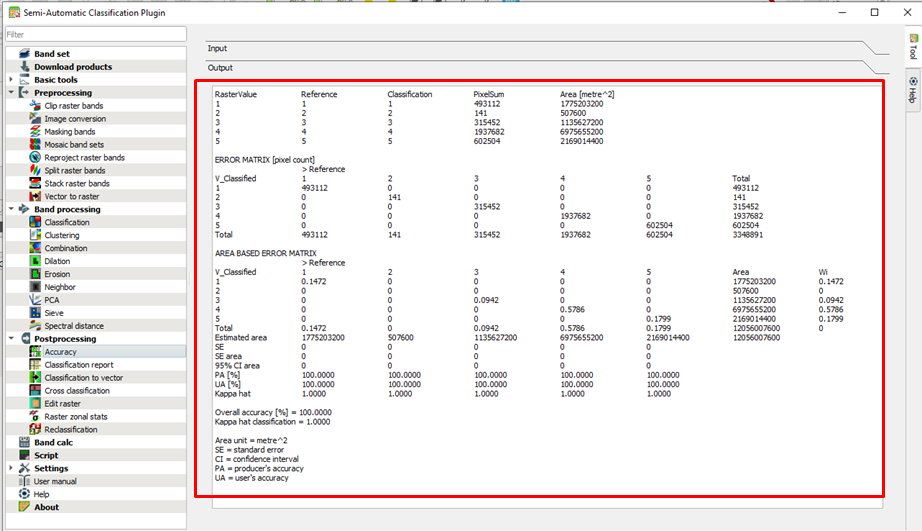
Матрица ошибок

Одним из наиболее развёрнутых способов оценки качества классификации является применение матрицы ошибок. Она представляет собой квадратную таблицу, в которой отображается количество предсказанных и фактических классов для классификационной модели.

В этой матрице:
- Строки представляют истинные классы (реальные метки).
- Столбцы представляют предсказанные классы (метки, которые предсказала модель).
- Размер матрицы соответствует количеству классов.

Обычно для бинарной классификации она выглядит так:

где:
- TP (True Positive) – истинно положительные примеры.
- TN (True Negative) – истинно отрицательные примеры.
- FP (False Positive) – ложноположительные примеры. ()
- FN (False Negative) – ложноотрицательные примеры.

Ошибки первого рода (ложноположительные ошибки, False Positive)

Note

Ошибки первого рода происходят, когда модель ошибочно относит объект к положительному классу.

Пример: алгоритм классификации земель неправильно относит участок к категории «застроенная территория», тогда как в действительности это сельскохозяйственные земли.

С учётом вышесказанного, ошибку первого рода часто называют ложной тревогой, ложным срабатыванием или ложноположительным срабатыванием. Если, например, анализ крови показал наличие заболевания, хотя на самом деле человек здоров, или металлодетектор выдал сигнал тревоги, сработав на металлическую пряжку ремня, то принятая гипотеза не верна, а следовательно совершена ошибка первого рода. Слово «ложноположительный» в данном случае не имеет отношения к желательности или нежелательности самого события.

Термин широко используется в медицине. Например, тесты, предназначенные для диагностики заболеваний, иногда дают положительный результат (то есть показывают наличие заболевания у пациента), когда на самом деле пациент этим заболеванием не страдает. Такой результат называется ложноположительным.

В других областях обычно используют словосочетания со схожим смыслом, например, «ложное срабатывание», «ложная тревога» и т. п. В информационных технологиях часто используют английский термин false positive без перевода.

Ошибки второго рода (ложноотрицательные ошибки, False Negative)

Note

Ошибки второго рода возникают, когда модель не распознаёт положительный класс и ошибочно относит его к отрицательному.

Пример: участок, который на самом деле относится к категории «водоём», был классифицирован как «растительность».

Соответственно, ошибку второго рода иногда называют пропуском события или ложноотрицательным срабатыванием. Человек болен, но анализ крови этого не показал, или у пассажира имеется холодное оружие, но рамка металлодетектора его не обнаружила (например, из-за того, что чувствительность рамки отрегулирована на обнаружение только очень массивных металлических предметов). Данные примеры указывают на совершение ошибки второго рода. Слово «ложноотрицательный» в данном случае не имеет отношения к желательности или нежелательности самого события.

В других областях обычно используют словосочетания со схожим смыслом, например, «пропуск события», и т. п.

Так как с ростом вероятности ошибки первого рода обычно уменьшается вероятность ошибки второго рода, и наоборот, настройка принимающей решение системы должна представлять собой компромисс. Где именно находится точка получаемого такой настройкой баланса, зависит от оценки последствий при совершении обоих видов ошибок.

Морфологичсекие операторы

В качестве входных данных для аппарата математической морфологии служат следующие изображения:

• Изображение, подлежащее обработке.
• Специальное изображение, которое зависит от типа операции и поставленной задачи.
  Данное специальное изображение называется примитивом или структурным компонентом. Обычно структурный компонент имеет гораздо меньшие размеры, чем обрабатываемое изображение. Структурный компонент может считаться описанием области с некоторой формой. Естественно, эта форма может иметь любую конфигурацию, но она должна обладать возможностью ее представления в формате бинарного изображения требуемых размеров.

В различных пакетах обработки изображений самые используемые структурные компоненты обладают следующими специальными названиями:

• B O X [H,W] является прямоугольником определенного размера.
• D I S K [R] является диском требуемого размера.
• R I N G [R] является кольцом заданного размера.

Результат морфологической обработки определяется как размером и конфигурацией исходного изображения, так и структурным примитивом.

Размеры структурного компонента обычно равняются 3x3, 4x4 или 5x5 пикселей. Это объясняется основной идеей морфологической обработки, в ходе которой следует отыскать характерные детали изображения. Искомая деталь должна быть описана примитивом, и в итоге морфологической обработки могут быть подчеркнуты или удалены такие детали на всем изображении.

Одним из главных достоинств морфологической обработки является ее простота, то есть, как на входе, так и на выходе операции обработки получается изображение в двоичном коде. Другие методики обычно из начального изображения вначале формируют полутоновое изображение, которое далее преобразуется в бинарное при помощи пороговых функций.

Главными операциями математической морфологии могут считаться следующие:

• Операция наращивания.
• Операция эрозии.
• Операция замыкания.
• Операция размыкания.

Данные названия отражают всю сущность этих операций:

• Операция наращивания способна увеличить область изображения.
• Операция эрозии способна сделать область изображения меньше.
• Операция замыкания предоставляет возможность замыкания внутренних отверстий области и устранения заливов вдоль границы области.
• Операция размыкания способна помочь избавиться от небольших фрагментов, которые выступают наружу области вблизи ее границы.

Объединением двух множеств A и B, обозначаемым как C=A∪B, является по определению множество всех элементов, которые принадлежат или множеству A, или множеству B, или обоим множествам одновременно. Пересечением двух множеств A и B, обозначаемым как C=A∩B, является по определению множество всех элементов, которые принадлежат одновременно обоим множествам A и B. Дополнением множества A является множество элементов, которые не содержатся в A:

Ac={w|w∉A}.

Разностью двух множеств A и B, обозначаемой как A\B, является следующее выражение:

A\B={w│w∈A,w∉B}=A∩Bc.

То есть, данное множество включает в свой состав все элементы множества A, не входящие в множество B.

Рассмотрим использование отдельных операций на конкретных примерах, представленных на рисунке ниже.

Операция переноса $X_t$ множества пикселей $X$ на вектор $t$ может быть представлена в виде:

$$X_t = x + t \, | \, x \in X$$

Это означает, что перенос множества единичных пикселей на двоичном изображении выполняет сдвиг всех пикселей множества на требуемое расстояние. Вектор переноса $t$ может быть представлен как упорядоченная пара:

$$(\Delta r, \Delta c)$$

где $\Delta r$ является элементом вектора переноса в направлении строк, а $\Delta c$ является элементом вектора переноса в направлении столбцов изображения.

Рассмотрим еще один конкретный пример. Допустим, имеется следующее бинарное изображение и структурный компонент:

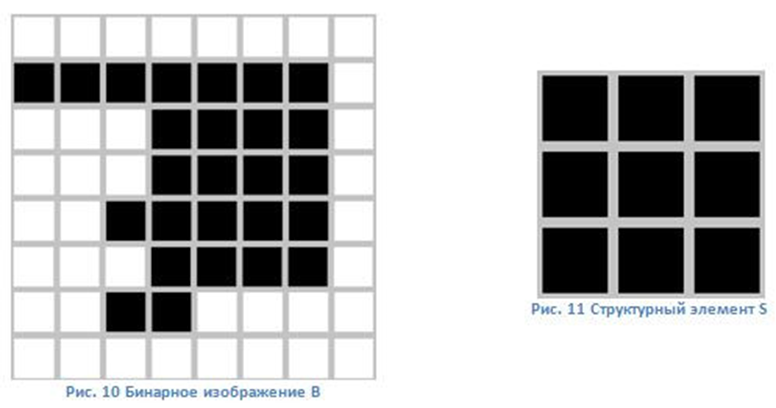
Структурный компонент $S$ следует применить ко всем пикселям двоичного изображения. Каждый раз, когда начало координат структурного компонента совмещается с единичным бинарным пикселем, ко всему структурному компоненту следует применить перенос и дальнейшее логическое сложение с требуемыми пикселями двоичного изображения. Итоги логического сложения должны быть записаны в выходное двоичное изображение, которое изначально было инициализировано при помощи нулевых значений.

При осуществлении операции эрозии структурный компонент также проходит по всем пикселям изображения. Если в определенной позиции каждый единичный пиксель структурного компонента имеет совпадение с единичным пикселем двоичного изображения, тогда следует выполнить логическое сложение центрального пикселя структурного компонента с необходимым пикселем выходного изображения.

Интерактивный демонстратор прилагается:

Постобработка реззультатов классифкации

Полученные карты классификации имеет смысл генерализировать перед векторизацией для чего могут быть использован операторы Эрозии и Дилатации расположенные в соотвествующей вкладке Band processing

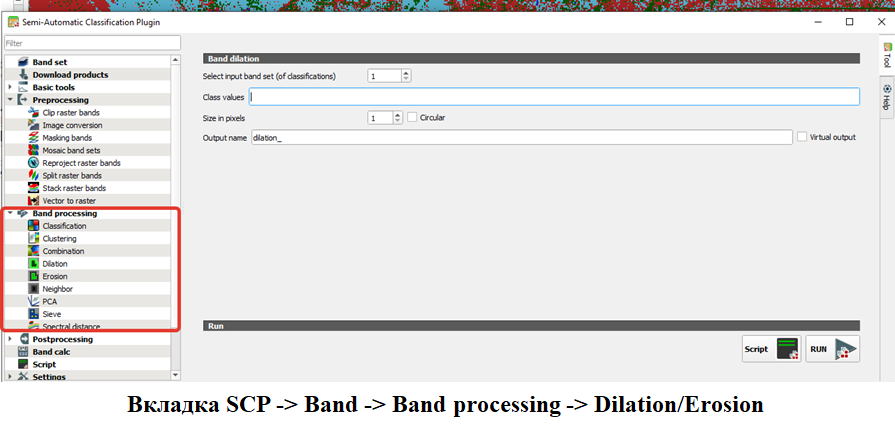
Однако использовав инструмент у вас открывается черно-белое изображение. Необходимо вернуть ему ту же цветую схему, что в и оригинальном изображении

Для чего скопируем стиль оформления у классифицированного растр (Cлои -> ПКМ по названию слоя -> Стили -> Копировать стиль,Cлои -> ПКМ по названию слоя -> Стили -> Применить стиль )

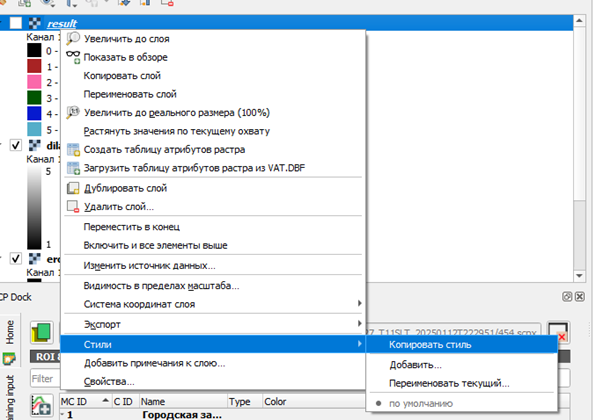
Результаты эрозии и дилатации применяются к классу. Посмотрите на оригинальное изображение и два обработанных и скажите, где какой оператор применялся?

Использованные истончики и материалы

1. (Проект VMATH)[https://vmath.ru/vf5/users/au/svm]