Практика 7 Понятие разделимости классов. Алгоритм SVM

Данные для занятия
Презентация

Наивный подход к разделимости классов

Картинки для демонстратора, скачайте и внесите в интерактивный тренажер.

Question

Как повторить подобную операцию в QGIS?

Общение для N-мерного пространства

Представим, что у меня уже 1 канал, а два, тогда они отобразятся в виде набора соотвествующих точек (x,y)

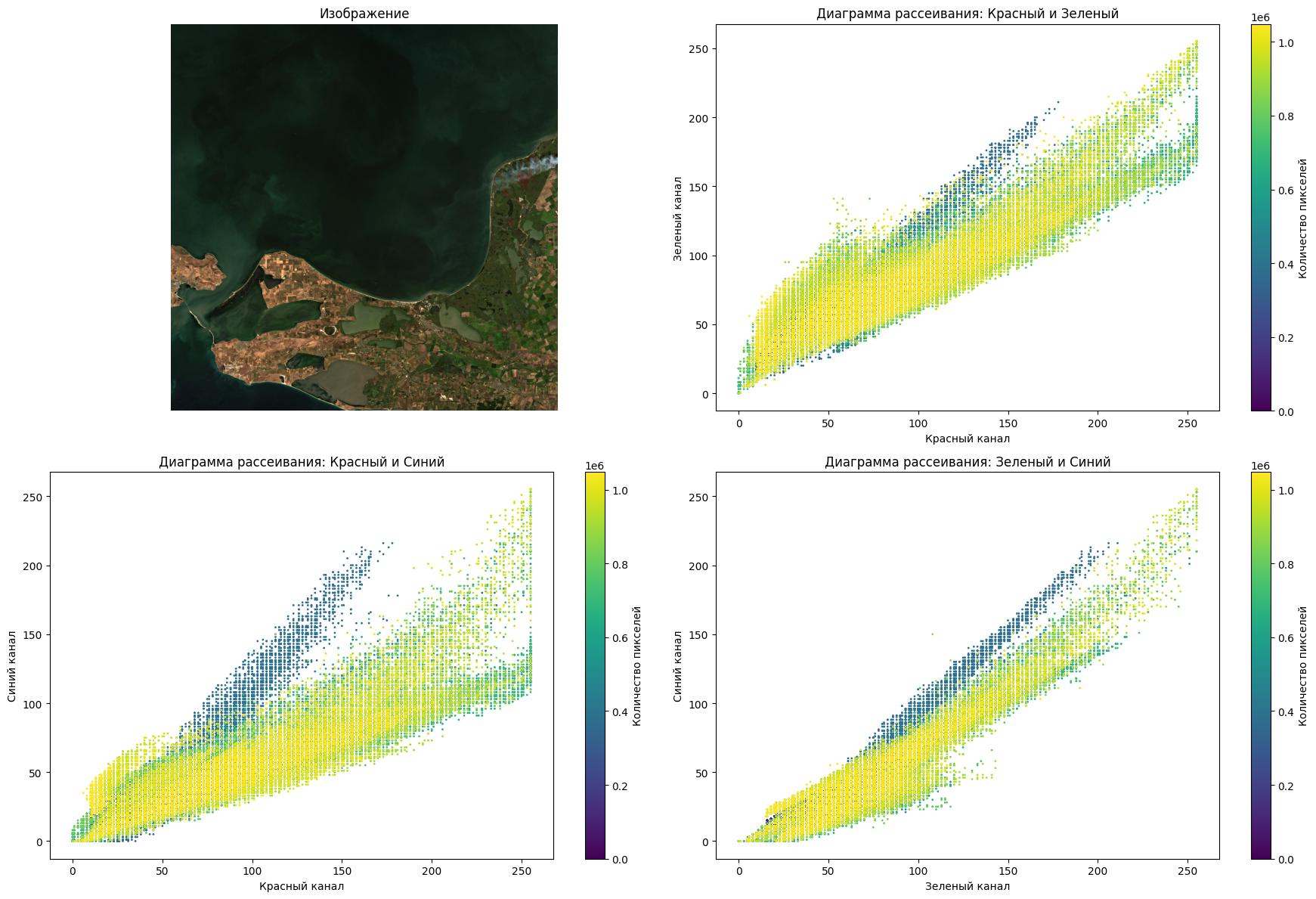
Question

Как можно разделить все точки на плоскость?

Question

Как можно разделить все точки в пространстве?

Метод опорных векторов (SVM)

Support Vector Machine (SVM) — это метод машинного обучения для решения задач классификации и регрессии. Основная идея заключается в нахождении оптимальной гиперплоскости, разделяющей данные с максимальным зазором между классами.

Основные концепции:

• Гиперплоскость — разделяющая поверхность, которая отделяет классы в пространстве признаков.
• Опорные вектора (Support Vectors) — точки, наиболее близкие к гиперплоскости, определяющие её положение.
• Максимальный зазор (Margin) — расстояние между гиперплоскостью и ближайшими точками каждого класса.
• Ядро (Kernel) — функция, позволяющая выполнять нелинейное разделение данных.

Метод опорных векторов в задаче классификации

Рассмотрим задачу бинарной классификации, в которой объектам из $X = \mathbb{R}^n$ соответствует один из двух классов $Y = \{-1, +1\}$.

Пусть задана обучающая выборка пар "объект-ответ": $T_\ell = \{( \vec{x}_i, y_i )\}_{i=1}^{\ell}$. Необходимо построить алгоритм классификации $a(\vec{x}): X \to Y$.

Разделяющая гиперплоскость

В пространстве $\mathbb{R}^n$ уравнение

$$\langle \vec{w}, \vec{x} \rangle - b = 0$$

при заданных $\vec{w}$ и $b$ определяет гиперплоскость — множество векторов $\vec{x} = (x_1, \dots, x_n)$, принадлежащих пространству меньшей размерности $\mathbb{R}^{n-1}$. Например, для $\mathbb{R}^1$ гиперплоскостью является точка, для $\mathbb{R}^2$ — прямая, для $\mathbb{R}^3$ — плоскость и т.д. Параметр $\vec{w}$ определяет вектор нормали к гиперплоскости, а через $b \|\vec{w}\|$ выражается расстояние от гиперплоскости до начала координат.

Гиперплоскость делит $\mathbb{R}^n$ на два полупространства:

$$\langle \vec{w}, \vec{x} \rangle - b > 0 \quad \text{и} \quad \langle \vec{w}, \vec{x} \rangle - b < 0.$$

Говорят, что гиперплоскость разделяет два класса $C_1$ и $C_2$, если объекты этих классов лежат по разные стороны от гиперплоскости, то есть выполнено либо

$$\langle \vec{w}, \vec{x} \rangle - b > 0, \quad \langle \vec{w}, \vec{x} \rangle - b < 0, \quad \forall \vec{x} \in C_1, \forall \vec{x} \in C_2,$$

либо

$$\langle \vec{w}, \vec{x} \rangle - b < 0, \quad \langle \vec{w}, \vec{x} \rangle - b > 0, \quad \forall \vec{x} \in C_1, \forall \vec{x} \in C_2.$$

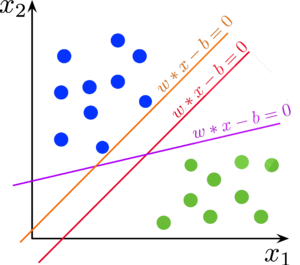
Демонстрация алгоритма SVM

Воспользуемся сервисом Демонстрация алгоритма SVM

Случай линейной разделимости

Пусть выборка линейно разделима, то есть существует некоторая гиперплоскость, разделяющая классы $-1$ и $+1$. Тогда в качестве алгоритма классификации можно использовать линейный пороговый классификатор:

$$a(\vec{x}) = \text{sign} \left( \langle \vec{w}, \vec{x} \rangle - b \right) = \text{sign} \left( \sum_{i=1}^{\ell} w_i x_i - b \right)$$

где $\vec{x} = (x_1, \dots, x_n)$ — вектор значений признаков объекта, а $\vec{w} = (w_1, \dots, w_n) \in \mathbb{R}^n$ и $b \in \mathbb{R}$ — параметры гиперплоскости.

Но для двух линейно разделимых классов возможны различные варианты построения разделяющих гиперплоскостей. Метод опорных векторов выбирает ту гиперплоскость, которая максимизирует отступ между классами:

Отступ (англ. margin) — характеристика, оценивающая, насколько объект "погружён" в свой класс, насколько типичным представителем класса он является. Чем меньше значение отступа $M_i$, тем ближе объект $\vec{x}_i$ подходит к границе классов и тем выше становится вероятность ошибки. Отступ $M_i$ отрицателен тогда и только тогда, когда алгоритм $a(\vec{x})$ допускает ошибку на объекте $\vec{x}_i$.

Для линейного классификатора отступ определяется уравнением:

$$M_i(\vec{w}, b) = y_i \left( \langle \vec{w}, \vec{x}_i \rangle - b \right)$$

Если выборка линейно разделима, то существует такая гиперплоскость, отступ от которой до каждого объекта положителен:

$$\exists \vec{w}, b : M_i(\vec{w}, b) = y_i \left( \langle \vec{w}, \vec{x}_i \rangle - b \right) > 0, \quad i = 1, \dots, \ell$$

Мы хотим построить такую разделяющую гиперплоскость, чтобы объекты обучающей выборки находились на наибольшем расстоянии от неё.

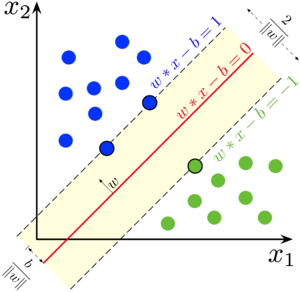
Заметим, что при умножении $\vec{w}$ и $b$ на константу $c \neq 0$ уравнение

$$\langle c \vec{w}, \vec{x} \rangle - c b = 0$$

определяет ту же самую гиперплоскость, что и $\langle \vec{w}, \vec{x} \rangle - b = 0$. Для удобства проведём нормировку: выберем константу $c$ таким образом, чтобы $\min M_i (\vec{w}, b) = 1$. При этом в каждом из двух классов найдётся хотя бы один "граничный" объект обучающей выборки, отступ которого равен этому минимуму: иначе можно было бы сместить гиперплоскость в сторону класса с большим отступом, тем самым увеличив минимальное расстояние от гиперплоскости до объектов обучающей выборки.

Обозначим любой "граничный" объект из класса $+1$ как $\vec{x}_+$, из класса $-1$ как $\vec{x}_-$. Их отступ равен единице, то есть

$$M_+(\vec{w}, b) = (+1) \left( \langle \vec{w}, \vec{x}_+ \rangle - b \right) = 1$$
$$M_-(\vec{w}, b) = (-1) \left( \langle \vec{w}, \vec{x}_- \rangle - b \right) = 1$$

Нормировка позволяет ограничить разделяющую полосу между классами: $\{ \vec{x} : -1 < \langle \vec{w}, \vec{x}_i \rangle - b < 1 \}$. Внутри неё не может лежать ни один объект обучающей выборки. Ширину разделяющей полосы можно выразить как проекцию вектора $\vec{x}_+ - \vec{x}_-$ на нормаль к гиперплоскости $\vec{w}$. Чтобы разделяющая гиперплоскость находилась на наибольшем расстоянии от точек выборки, ширина полосы должна быть максимальной:

$$\langle \vec{x}_+ - \vec{x}_-, \vec{w} \rangle \| \vec{w} \| = \langle \vec{x}_+, \vec{w} \rangle - \langle \vec{x}_-, \vec{w} \rangle - b + b \| \vec{w} \| = (+1) \left( \langle \vec{x}_+, \vec{w} \rangle - b \right) + (-1) \left( \langle \vec{x}_-, \vec{w} \rangle - b \right) \| \vec{w} \| = M_+(\vec{w}, b) + M_-(\vec{w}, b) \| \vec{w} \| = 2 \| \vec{w} \| \rightarrow \max \Rightarrow \| \vec{w} \| \rightarrow \min$$

Это приводит нас к постановке задачи оптимизации в терминах квадратичного программирования:

$$\| \vec{w} \|^2 \rightarrow \min \quad \text{при условии} \quad M_i (\vec{w}, b) \geq 1, \quad i = 1, \dots, \ell$$

Линейно неразделимая выборка

На практике линейно разделимые выборки практически не встречаются: в данных возможны выбросы и нечёткие границы между классами. В таком случае поставленная выше задача не имеет решений, и необходимо ослабить ограничения, позволив некоторым объектам попадать на "территорию" другого класса. Для каждого объекта отнимем от отступа некоторую положительную величину $\xi_i$, но потребуем, чтобы эти введённые поправки были минимальны. Это приведёт к следующей постановке задачи, называемой также SVM с мягким отступом (англ. soft-margin SVM):

$$\begin{aligned} \min_{w, b, \xi} \quad & \frac{1}{2} \| \vec{w} \|^2 + C \sum_{i=1}^{\ell} \xi_i \\ \text{при условии} \quad & M_i(\vec{w}, b) \geq 1 - \xi_i, \quad i = 1, \dots, \ell \\ & \xi_i \geq 0, \quad i = 1, \dots, \ell \end{aligned}$$

Мы не знаем, какой из функционалов $\frac{1}{2} \| \vec{w} \|^2$ и $\sum_{i=1}^{\ell} \xi_i$ важнее, поэтому вводим коэффициент $C$, который будем оптимизировать с помощью кросс-валидации. В итоге мы получили задачу, у которой всегда есть единственное решение.

Заметим, что мы можем упростить постановку задачи:

$$\begin{aligned} \xi_i \geq 0, \\ \xi_i \geq 1 - M_i(\vec{w}, b), \\ \sum_{i=1}^{\ell} \xi_i \rightarrow \min \quad \Rightarrow \quad \xi_i = \max(0, 1 - M_i(\vec{w}, b)), \\ \sum_{i=1}^{\ell} \xi_i \rightarrow \min \quad \Rightarrow \quad \xi_i = (1 - M_i(\vec{w}, b))^+. \end{aligned}$$

Получим эквивалентную задачу безусловной минимизации:

$$\min_{w, b} \quad \frac{1}{2} \| \vec{w} \|^2 + C \sum_{i=1}^{\ell} (1 - M_i(\vec{w}, b))^+.$$

Нелинейное обобщение, kernel trick

Существует ещё один подход к решению проблемы линейной разделимости, известный как трюк с ядром (kernel trick). Если выборка объектов с признаковым описанием из $X = \mathbb{R}^n$ не является линейно разделимой, мы можем предположить, что существует некоторое пространство $H$, вероятно, большей размерности, при переходе в которое выборка станет линейно разделимой. Пространство $H$ здесь называют спрямляющим, а функцию перехода $\psi : X \to H$ — спрямляющим отображением. Построение SVM в таком случае происходит так же, как и раньше, но в качестве векторов признаковых описаний используются векторы $\psi(\vec{x})$, а не $\vec{x}$. Соответственно, скалярное произведение $\langle \vec{x}_1, \vec{x}_2 \rangle$ в пространстве $X$ везде заменяется скалярным произведением $\langle \psi(\vec{x}_1), \psi(\vec{x}_2) \rangle$ в пространстве $H$. Отсюда следует, что пространство $H$ должно быть гильбертовым, так как в нём должно быть определено скалярное произведение.

Обратим внимание на то, что постановка задачи и алгоритм классификации не используют в явном виде признаковое описание и оперируют только скалярными произведениями признаков объектов. Это даёт возможность заменить скалярное произведение в пространстве $X$ на ядро — функцию, являющуюся скалярным произведением в некотором $H$. При этом можно вообще не строить спрямляющее пространство в явном виде, и вместо подбора $\psi$ подбирать непосредственно ядро.

Постановка задачи с применением ядер приобретает вид:

$$\begin{aligned} \min_{\lambda} \quad & -L(\lambda) = -\sum_{i=1}^{\ell} \lambda_i + \frac{1}{2} \sum_{i=1}^{\ell} \sum_{j=1}^{\ell} \lambda_i \lambda_j y_i y_j K(\vec{x}_i, \vec{x}_j) \\ \text{при условиях} \quad & \lambda_i \geq 0, \quad i = 1, \dots, \ell \\ & \sum_{i=1}^{\ell} \lambda_i y_i = 0 \end{aligned}$$

Алгоритм классификации будет:

$$a(\vec{x}) = \text{sign} \left( \sum_{i=1}^{\ell} \lambda_i y_i K(\vec{x}_i, \vec{x}) - b \right)$$

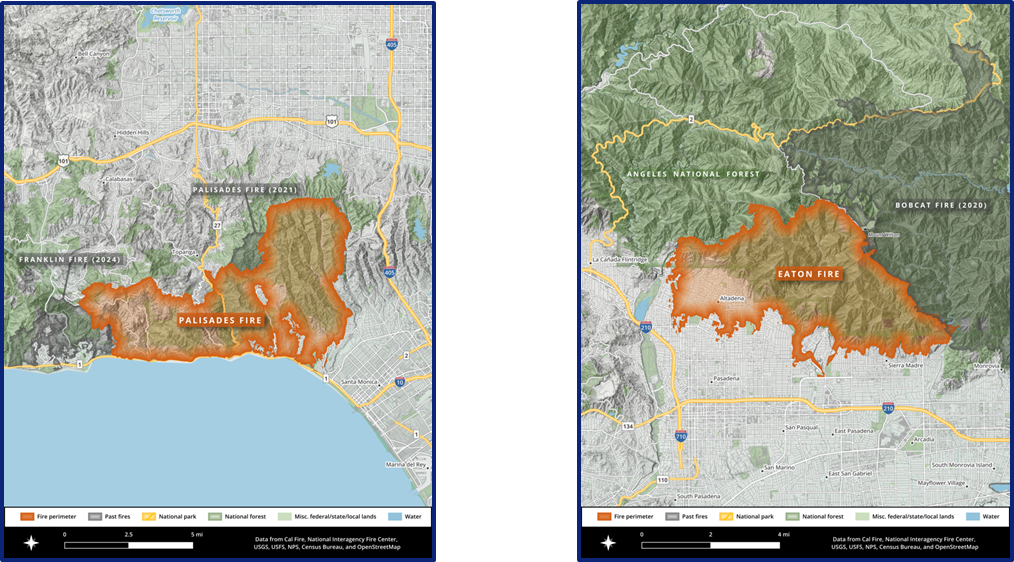
Исследование пожаров Калифорнии (2025)

В январе 2025 года в Калифорнии бушевали лесные пожары. Возгорание началось 7 января, а вечером 9 января огонь достиг голливудских холмов.
По данным пожарной службы штата на 10 января, огонь охватил более 11 тыс. га и уничтожил около 5 тыс. строений

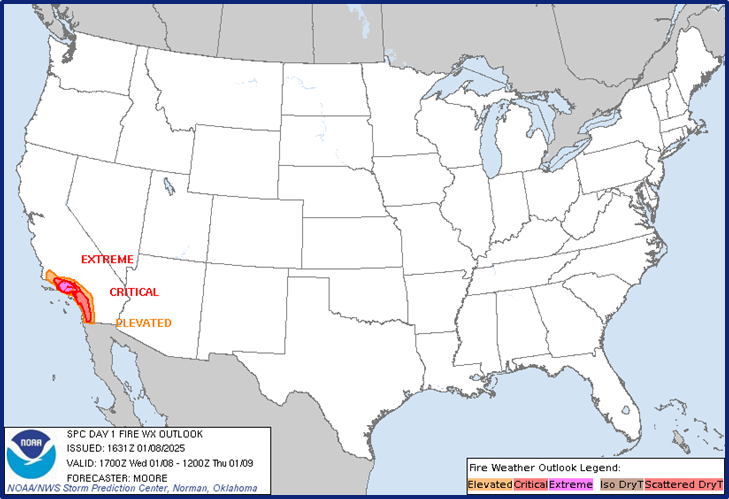
Что известно о явлении:
- В 2025 году наблюдается увеличение числа пожаров в северных районах Калифорнии.
- Основными причинами возгораний стали засуха и сильные ветры.

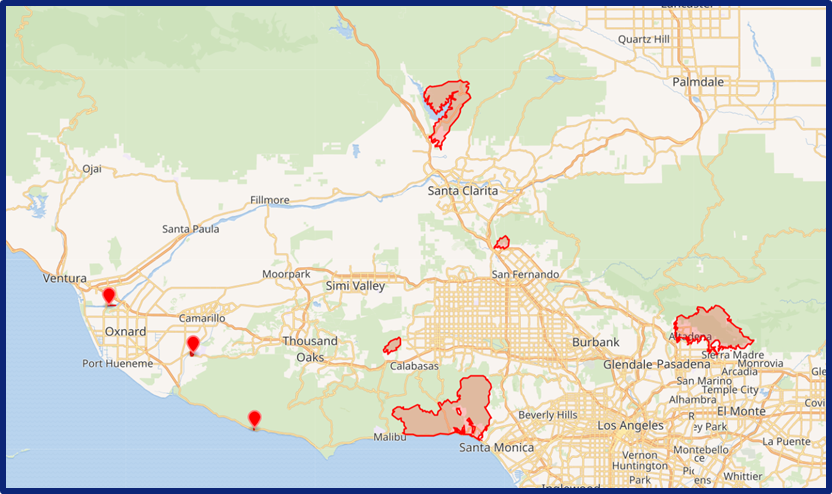
Псевдоцветные снимки со спутника Aqua на пожары в Палисейдс, Хёрст и Итон. 8 января, 21:40 GMT / 1:40 вечера PST.

Калифорнийский государственный геопортал

Калифорнийский государственный геопортал (California State Geoportal) — это централизованный портал геопространственных данных, предоставляющий доступ к официальным картографическим материалам штата. Он включает данные различных государственных агентств, охватывающие темы экологии, инфраструктуры, землепользования и природных катастроф.

Для анализа пожаров будет использован набор данных "CAL FIRE Statewide Fire Perimeters" (ссылка), содержащий границы лесных пожаров в формате GeoJSON.

Набор данных WFIGS 2025 Wildfire Perimeters

Этот набор данных содержит актуальную информацию о периметрах лесных пожаров в США за 2025 год. Источник данных — Национальный межведомственный центр пожаротушения (NIFC). Информация обновляется в режиме реального времени и используется для мониторинга пожаров, планирования эвакуации и оценки ущерба.

Что содержит данный набор?

• Границы лесных пожаров по всей Калифорнии.
• Атрибутивные данные: название пожара, дата обнаружения, площадь, статус ликвидации.
• Источник данных: California Department of Forestry and Fire Protection (CAL FIRE).

Подготовка данных ДЗЗ

Воспользуемся плагином STACK API Browser для загрузки спутниковых снимков.
Параметры запроса:
- Спутник: Sentinel-2A
- Период: 12 января – 30 января 2025 года (пик пожаров)
- Максимальная облачность: 30%
- Территория анализа: зона пожара Palisades

Работа с плагином SCP

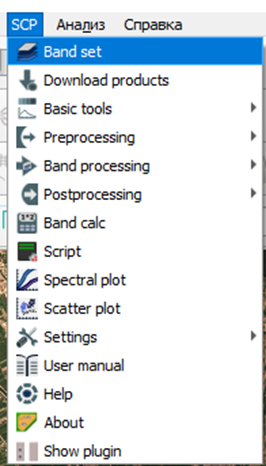
Загрузите снимки. Найдите вкладку SCP и выберите Band Set, как это сделано на рисунке

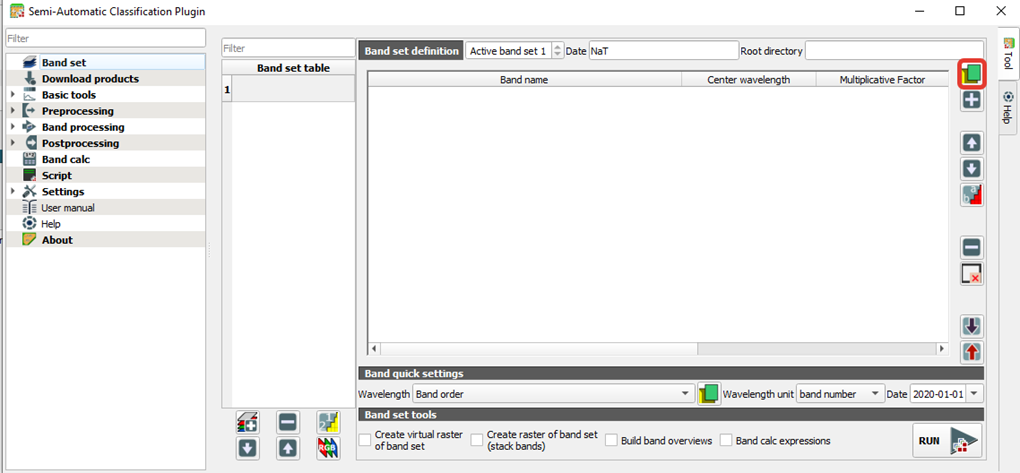
При нажатии откроется окно, в котором будут собраны все инструменты плагина, однако сосредоточимся на открытии данных
Нажмите на значок выделенный красным

После выбора tif файла можно несколько наборов каналов. Выберите набор каналов. Для отображения композита (наборов каналов) нажмите кнопку RGB.
Переставьте в полученном изображении каналы (нажмите на слой ПКМ и выбирите свойства-> стиль. Поменяйте 1 и 3 канал местами), если это необходимо

Формирование обучающей выборки

Для начала работы перейдите во вкладку Training Input в левом нижнем окне.

Выберите место, куда будут сохранены данные по нарисованным нами областям ROI

Для формирования обучающей выборки найдите инструмент Наращивание областей.

Поставьте параметр d = 0.1. Отметьте несколько областей в рамках одного класса. Для этого нажмите ctrl и щелкните на область. Добавьте не менее 3 примеров для каждого класса.

• Гари MC ID= 1, C id = 1
• Поля MC ID= 2, C id = 1
• Городская застройка MC ID= 3, C id = 1
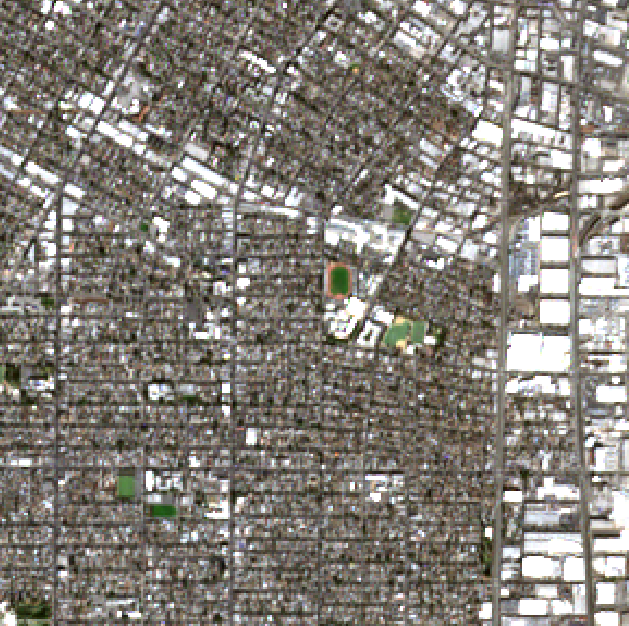
• Вода MC ID= 4, C id = 1
• Гористая местность MC ID= 5, C id = 1

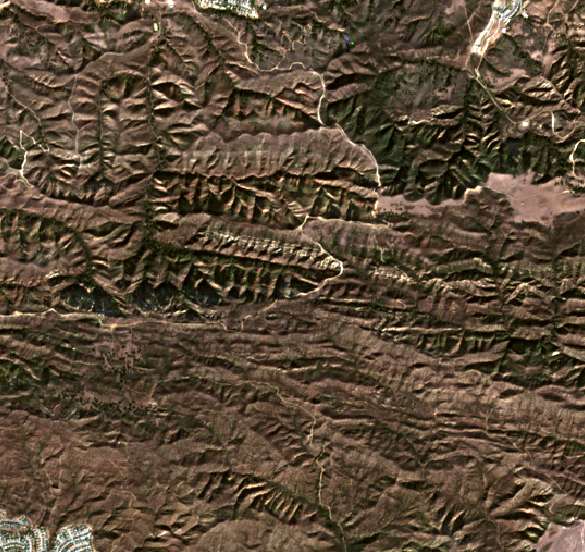
Note

Самостоятельно найтите воду второго типа

Алогоритм наращивания областей

Алгоритм наращивания областей позволяет выбирать пиксели, похожие на исходный, на основе спектрального сходства (спектрального расстояния) между соседними пикселями. В Semi-Automatic Classification Plugin (SCP) этот алгоритм используется для создания обучающих областей.

Параметры алгоритма:
- Спектральное расстояние — определяет степень сходства пикселей. Чем меньше значение, тем более похожие пиксели включаются в область.
- Максимальная ширина — задает длину стороны квадрата, центрированного на исходном пикселе, внутри которого формируется обучающая область (при одинаковых значениях пикселей она охватила бы весь квадрат).
- Минимальный размер — ограничивает процесс выбора, гарантируя, что в обучающую область попадут хотя бы те пиксели, которые наиболее похожи на исходный, пока их количество не достигнет заданного порога.

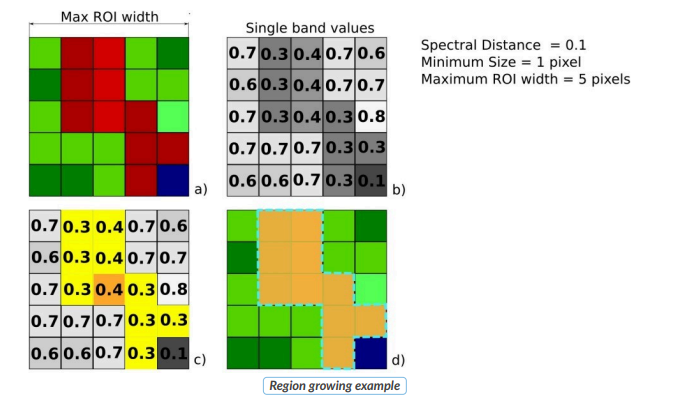
На изображении Region Growing Example центральный пиксель используется как исходный (a). Затем алгоритм выделяет область на основе одной спектральной полосы (b) с параметром spectral distance = 0.1. В результате формируется обучающая область, содержащая похожие пиксели (c и d).

Классификация по спектральным сигнатурам (Land Cover Signature Classification)

Note

Спектральная сигнатура — это изменение коэффициента отражения или излучения материала в зависимости от длины волны.

Данный метод классификации определяет спектральные пороговые значения для каждого обучающего класса (минимальное и максимальное значение для каждой спектральной полосы). Пороговые значения формируют спектральную область, соответствующую определенному классу земного покрова.

Принцип работы:
1. Спектральные подписи пикселей сравниваются с обучающими спектральной сигнатурой.
2. Пиксель относят к классу X, если его спектральная подпись полностью находится в спектральной области, определенной для X.
3. Если пиксель попадает в зону перекрытия нескольких классов или не принадлежит ни одной спектральной области, применяются дополнительные алгоритмы классификации (например, Minimum Distance, Maximum Likelihood, Spectral Angle Mapping).

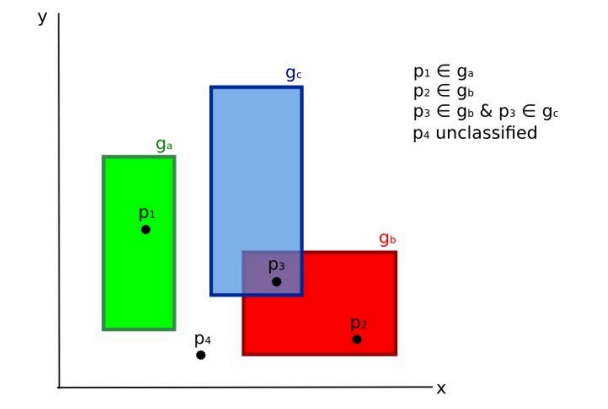
На схеме ниже показана классификация по спектральным подписям для двух спектральных каналов.
Определены три класса (ga, gb, gc):
- Точка p1 относится к классу ga.
- Точка p2 принадлежит классу gb.
- Точка p3 находится в пересечении классов gb и gc, поэтому останется неклассифицированной или будет обработана дополнительным алгоритмом.
- Точка p4 не принадлежит ни одной области и также останется неклассифицированной или будет обработана дополнительным алгоритмом.
- Если точка p4 все же относится к классу gc, спектральную область gc можно расширить, включив p4.

Сравнение классификацией по спектральным областям (Parallelepiped Classification)

Этот метод похож на Parallelepiped Classification, но спектральные области задаются вручную, независимо для верхней и нижней границ.
Спектральные области можно представить как множество всех возможных спектральных подписей пикселей, относящихся к одному классу.

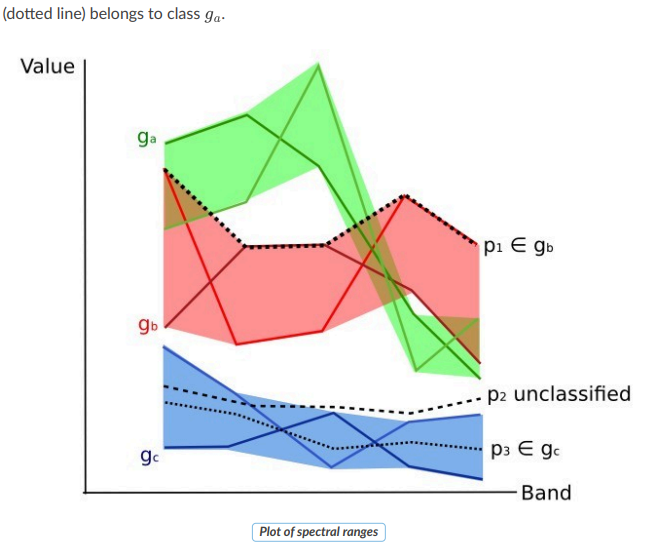
На графике ниже показаны спектральные диапазоны трех классов (ga, gb, gc):
- Цветные линии внутри диапазонов представляют спектральные подписи пикселей, определившие границы.
- Пиксель p1 (пунктирная линия) относится к классу gb, так как его спектральная подпись полностью находится в его диапазоне.
- Пиксель p2 (штриховая линия) не классифицируется, так как его спектральная подпись не попадает ни в один диапазон.
- Пиксель p3 (пунктирная линия) относится к классу ga.

Преимущества метода

• Позволяет точно определять классы, устанавливая четкие спектральные пороги.
• Может быть использован для выделения конкретного класса земного покрова, оставляя остальную часть изображения неклассифицированной.
• Подходит для ситуаций, когда классы различаются только по одной спектральной полосе.
• Обеспечивает точное представление ожидаемой классификации, если правильно заданы пороговые значения.

Исследование спектральных сигнатур

Для исследования спектральных сигнатуре в SCP есть два инструмента Add hightliht signature to signature plot и dd hightliht signature to scatter plot

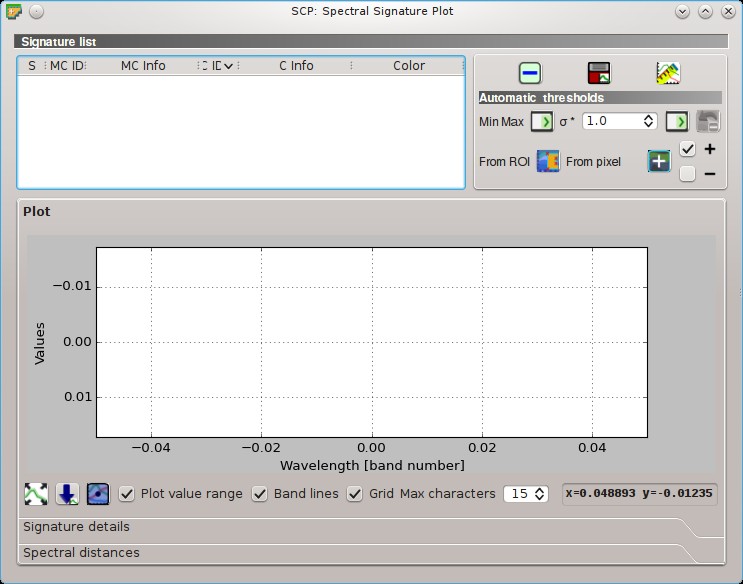
Spectral Signature Plot

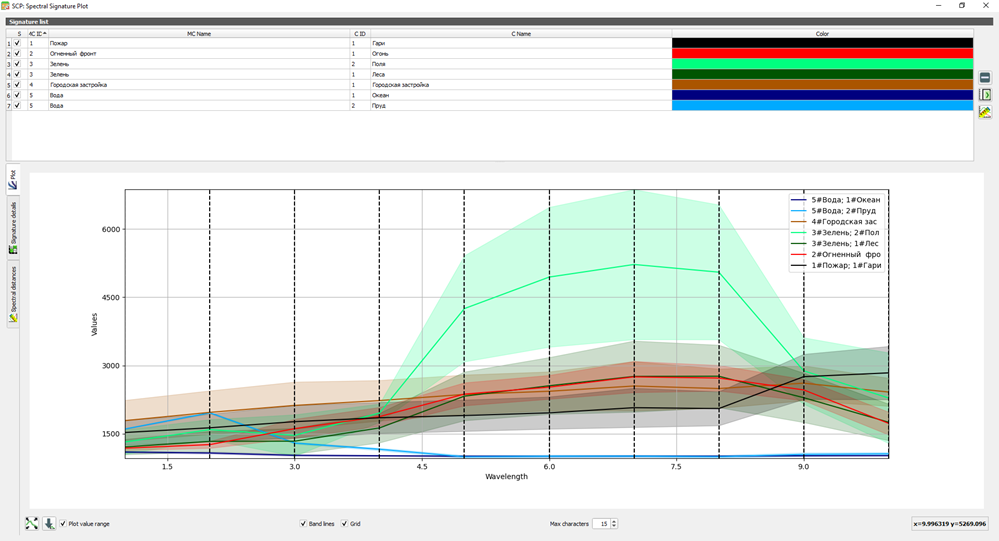
Окно Spectral Signature Plot включает несколько функций для отображения значений спектральных сигнатур в зависимости от длины волны (определенной в наборе полос). Подписи можно добавить в Spectral Signature Plot через панель SCP.

Окно также включает функции, полезные для определения диапазонов значений, используемых в классификации по спектральным сигнатруами земного покрова

Перекрывающиеся подписи (относящиеся к разным классам или макроклассам) выделяются оранжевым цветом в таблице Plot Signature list. Проверка на перекрытие выполняется с учетом MC ID или C ID в зависимости от настройки флажка Use checkbox MC ID или checkbox C ID в алгоритме классификации. Перекрывающиеся подписи с одинаковым ID не выделяются.

Команды для работы с графиком

• Перемещение: Левый клик и удерживание внутри графика позволяет перемещать вид графика. Использование колесика мыши позволяет зумировать график (вблизи и вдали).
• Зум по области: Правый клик и удерживание внутри графика позволяет увеличить конкретную область графика.
• Перемещение легенды: Легенду внутри графика можно перемещать с помощью мыши.

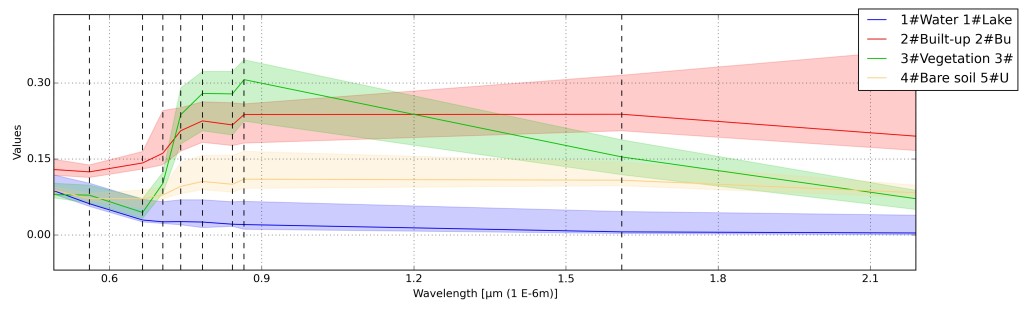
Команды для работы с графиком:

• fit_plot: автоматически подгоняет график под данные.
• save_plot_image: сохраняет изображение графика в файл (доступные форматы: .jpg, .png, .pdf).
• sign_edit_range: активирует курсор для изменения диапазона значений выделенных сигнатуры в графике. Клик на график позволяет задать минимальное или максимальное значение для полосы (можно для нескольких сигнатур одновременно). Курсор деактивируется при выходе за пределы области графика.
• checkbox Plot value range: если отмечено, отображается диапазон значений для каждой сигнатуры (полупрозрачная область).
• checkbox Band lines: если отмечено, отображаются вертикальные линии для каждой полосы (центральная длина волны).
• checkbox Grid: если отмечено, отображается сетка.
• Max characters input_number: задает максимальную длину текста в легенде.
• x y: отображает координаты x и y курсора мыши внутри графика.

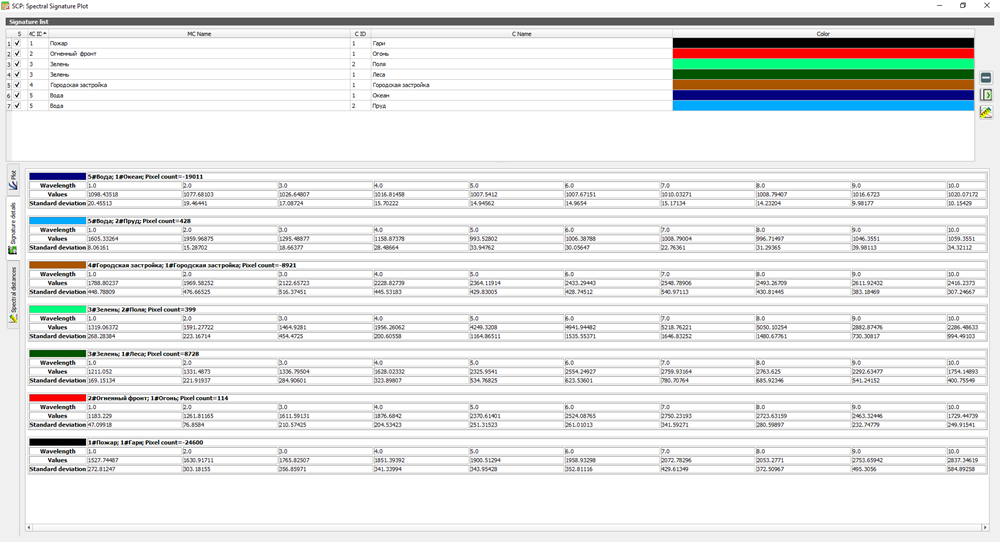
Signature details

Отображает детали спектральных сигнатур (т.е. длина волны, значения и стандартное отклонение). В случае сигнатур, рассчитанных на основе ROI, также отображается размер ROI (количество пикселей).

Спектральные расстояния

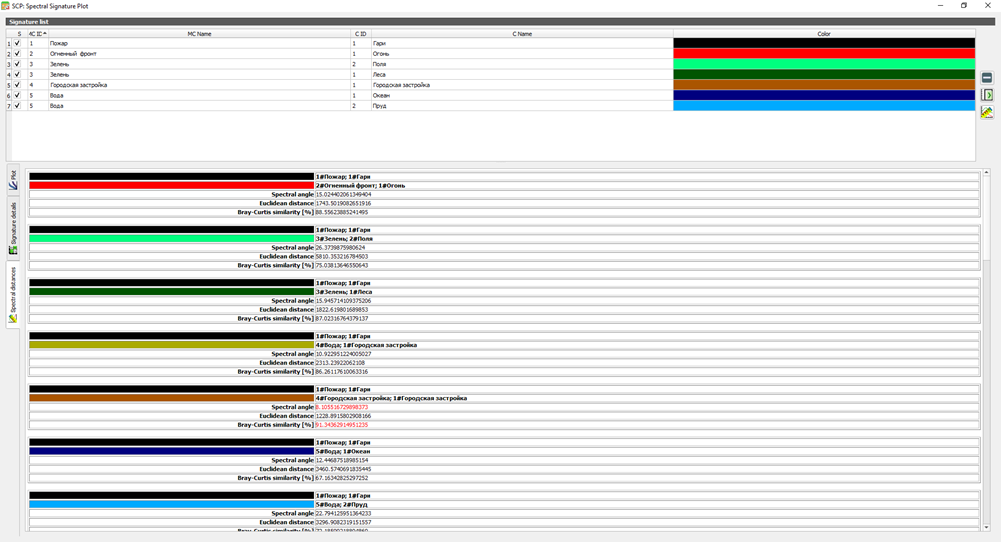
Отображает спектральные расстояния сигнатур (см. Plot Signature list), которые полезны для оценки разделимости ROI (см. Spectral Distance).

Расчитываемые спектральные расстояния:

• Jeffries-Matusita Distance: диапазон [0 = одинаковые, 2 = разные]; полезно, в частности, для классификации методом Maximum Likelihood;
• Spectral Angle: диапазон [0 = одинаковые, 90 = разные]; полезно для классификации методом Spectral Angle Mapping;
• Euclidean Distance: полезно для классификации методом Minimum Distance;
• Bray-Curtis Similarity: диапазон [0 = разные, 100 = одинаковые]; полезно в общем случае.

Значения отображаются красным, если сигнатуры особенно похожи.

Spectral Angle (Спектральный угол)

• Диапазон: от 0 (одинаковые спектры) до 90 (совершенно разные спектры).
• Описание: Это метрика, измеряющая угол между двумя спектральными векторами. Чем меньше угол, тем более схожи спектры. В классификации Spectral Angle Mapping (SAM) используется этот угол для оценки, насколько близки спектры пикселей к определенному эталону (например, определенному классу).
• Зачем: Спектральный угол полезен для классификации объектов, где важно оценить, насколько схожи спектры между собой, независимо от их интенсивности. Например, для идентификации растений или минералов, где спектры могут сильно отличаться по форме, но быть схожими по углу.

Euclidean Distance (Евклидово расстояние)

• Описание: Это стандартная метрика для измерения прямого расстояния между двумя точками в многомерном пространстве (например, спектры в многополосных изображениях). Чем меньше расстояние, тем более схожи два спектра.
• Зачем: В классификации методом Minimum Distance (минимальное расстояние) используется эта метрика, чтобы выбрать класс для пикселя, который имеет минимальное расстояние до центра класса в спектральном пространстве. Это простой и эффективный метод для классификации, где важно быстро определить, какой класс наиболее близок к данному пикселю.

Bray-Curtis Similarity (Сходство по Брэю-Кертису)

• Диапазон: от 0 (совсем разные) до 100 (совсем одинаковые).
• Описание: Это метрика, которая измеряет схожесть между двумя спектрами, основываясь на их относительных значениях. Она учитывает только присутствие или отсутствие значений, игнорируя абсолютные значения. Подходит для анализа данных, где важно оценить сходство на основе пропорций или составов.
• Зачем: Используется для оценки сходства в более широком контексте, когда данные могут быть более разнообразными, и мы хотим понять, насколько они похожи по составу, а не по абсолютным значениям. Это может быть полезно в общем случае для классификации, например, при анализе экосистем или при оценке изменений в составах земельных покрытий.