Лекция 7 Обратимость матриц. Псевдообратная матрица. МНК в матричной форме

Презентация доступна здесь

Обратная матрица: определение, существование и единственность

Рассмотрим проблему определения операции, обратной умножению матриц.

Пусть A — квадратная матрица порядка n. Матрица $A^{-1}$, удовлетворяющая вместе с заданной матрицей A равенствам:

$$A^{-1} \cdot A = A \cdot A^{-1} = E,$$

называется обратной. Матрицу A называют обратимой, если для неё существует обратная, в противном случае — необратимой.

Из определения следует, что если обратная матрица $A^{-1}$ существует, то она квадратная того же порядка, что и A. Однако не для всякой квадратной матрицы существует обратная. Если определитель матрицы A равен нулю:

$$\det A = 0,$$

то для неё не существует обратной. В самом деле, применяя теорему об определителе произведения матриц к единичной матрице $E = A^{-1} A$, получаем противоречие:

$$\det E = \det(A^{-1} \cdot A) = \det A^{-1} \cdot \det A = \det A^{-1} \cdot 0 = 0,$$

тогда как $\det E = 1$. Следовательно, отличие определителя квадратной матрицы от нуля является единственным условием существования обратной матрицы. Напомним, что квадратную матрицу, определитель которой равен нулю, называют вырожденной (особой), в противном случае — невырожденной (неособой).

---

Теорема о существовании и единственности обратной матрицы

Квадратная матрица

$$A = \begin{pmatrix} a_{11} & \cdots & a_{1n} \\ \vdots & \ddots & \vdots \\ a_{n1} & \cdots & a_{nn} \end{pmatrix},$$

определитель которой отличен от нуля, имеет обратную матрицу и притом только одну:

$$A^{-1} = \frac{1}{\det A} \cdot \begin{pmatrix} A_{11} & A_{21} & \cdots & A_{1n} \\ A_{12} & A_{22} & \cdots & A_{n2} \\ \vdots & \vdots & \ddots & \vdots \\ A_{1n} & A_{2n} & \cdots & A_{nn} \end{pmatrix} = \frac{1}{\det A} \cdot A^{+},$$

где $A^{+}$ — матрица, транспонированная к матрице, составленной из алгебраических дополнений элементов A.

Матрица $A^{+}$ называется присоединённой матрицей по отношению к A.

Матрица $\frac{1}{\det A} A^{+}$ существует при условии $\det A \ne 0$. Нужно показать, что она обратна к A, то есть удовлетворяет двум условиям:

$$\begin{aligned} \text{1)} & \quad A \cdot \left(\frac{1}{\det A} \cdot A^{+}\right) = E, \\ \text{2)} & \quad \left(\frac{1}{\det A} \cdot A^{+}\right) \cdot A = E. \end{aligned}$$

Докажем первое равенство. Согласно замечанию 2.3, из свойств определителя следует, что:

$$A A^{+} = \det A \cdot E.$$

Следовательно:

$$A \cdot \left(\frac{1}{\det A} \cdot A^{+}\right) = \frac{1}{\det A} \cdot A A^{+} = \frac{1}{\det A} \cdot \det A \cdot E = E.$$

Аналогично доказывается второе равенство.

Итак, при $\det A \ne 0$ матрица A имеет обратную:

$$A^{-1} = \frac{1}{\det A} \cdot A^{+}.$$

Единственность: допустим, существует ещё одна обратная матрица B (где $B \ne A^{-1}$), такая что:

$$A B = E.$$

Умножим обе части этого равенства слева на $A^{-1}$:

$$A^{-1} A B = A^{-1} E \Rightarrow E B = A^{-1} \Rightarrow B = A^{-1},$$

что противоречит $B \ne A^{-1}$. Значит, обратная матрица единственна.

---

Замечания

1. Из определения следует, что матрицы A и $A^{-1}$ перестановочны.

2. Обратная к невырожденной диагональной матрице — тоже диагональная:

$$\left[ \operatorname{diag}(a_{11}, a_{22}, \ldots, a_{nn}) \right]^{-1} = \operatorname{diag} \left(\frac{1}{a_{11}}, \frac{1}{a_{22}}, \ldots, \frac{1}{a_{nn}}\right).$$

1. Обратная к невырожденной нижней (или верхней) треугольной матрице — тоже нижняя (или верхняя) треугольная.

2. Элементарные матрицы имеют обратные, которые также являются элементарными.

Свойства обратной матрицы

Операция обращения матрицы обладает следующими свойствами:

$$\begin{aligned} \bold{1.}&~~ (A^{-1})^{-1} = A\,;\\[3pt] \bold{2.}&~~ (AB)^{-1} = B^{-1} A^{-1}\,;\\[3pt] \bold{3.}&~~ (A^T)^{-1} = (A^{-1})^T\,;\\[3pt] \bold{4.}&~~ \det(A^{-1}) = \frac{1}{\det A}\,;\\[3pt] \bold{5.}&~~ E^{-1} = E\,. \end{aligned}$$

где все указанные операции имеют смысл (матрицы квадратные и невырожденные).

---

Доказательство свойства 2

Если произведение двух квадратных невырожденных матриц A и B определено, то обратная к произведению матрица равна:

$$(AB)^{-1} = B^{-1} A^{-1}.$$

Доказательство:

Определитель произведения матриц:

$$\det(AB) = \det A \cdot \det B,$$

а значит, $\det(AB) \ne 0$, если $\det A \ne 0$ и $\det B \ne 0$, то есть матрица AB также невырожденная и имеет обратную.

Проверим по определению, что $B^{-1} A^{-1}$ является обратной по отношению к $AB$:

$$\begin{aligned} (AB)(B^{-1} A^{-1}) &= A \cdot (B B^{-1}) \cdot A^{-1} = A \cdot E \cdot A^{-1} = A A^{-1} = E, \\[5pt] (B^{-1} A^{-1})(AB) &= B^{-1} \cdot (A^{-1} A) \cdot B = B^{-1} E B = B^{-1} B = E. \end{aligned}$$

Так как обратная матрица существует и единственна, получаем:

$$(AB)^{-1} = B^{-1} A^{-1}.$$

Свойство доказано.

Остальные свойства можно доказать аналогично.

---

Замечания

1. Для комплексной матрицы справедливо равенство, аналогичное свойству 3:

$$(A^{\ast})^{-1} = (A^{-1})^{\ast},$$

где символ $\ast$ обозначает сопряжённую (эрмитову) матрицу.

1. Операция обращения позволяет определить целую отрицательную степень невырожденной матрицы A. Для любого натурального числа n:

$$A^{-n} = (A^{-1})^n.$$

Способы нахождения обратной матрицы

Пусть дана квадратная матрица A. Требуется найти обратную матрицу $A^{-1}$.

Первый способ — через присоединённую матрицу

Описан в теореме 4.1 (о существовании и единственности обратной матрицы):

1. Вычислить определитель $\det A$.
   Если $\det A = 0$, то обратной матрицы не существует (матрица вырожденная).

2. Составить матрицу из алгебраических дополнений $A_{ij} = (-1)^{i+j} M_{ij}$, где $M_{ij}$ — минор элемента $a_{ij}$. Обозначим:

$$\begin{pmatrix} A_{ij} \end{pmatrix}$$

1. Транспонировать эту матрицу:
   Получим присоединённую матрицу:

$$A^{+} = (A_{ij})^{T}$$

1. Разделить все элементы присоединённой матрицы на $\det A$:

$$A^{-1} = \frac{1}{\det A} \cdot A^{+}$$

---

Второй способ — метод элементарных преобразований

1. Составить блочную матрицу $(A \mid E)$, приписав к A единичную матрицу E того же порядка.

2. С помощью элементарных преобразований строк привести левый блок A к простейшему виду $\Lambda$.
   При этом:

$$(A \mid E) \rightarrow (\Lambda \mid S)$$

где S — квадратная матрица, полученная из E.

1. Если $\Lambda = E$, то $S = A^{-1}$.
   Если $\Lambda \ne E$, то обратной матрицы не существует.

Обоснование:

Преобразования приводят блочную матрицу к виду $(\Lambda \mid S)$, где выполняется:

$$\Lambda = SA$$

Если A невырожденная, то $\Lambda = E$, и, следовательно, $SA = E \Rightarrow S = A^{-1}$.
Если A вырожденная, то $\Lambda \ne E$, и обратной матрицы не существует.

---

Замечания

1. Обратная матрица второго порядка

Пусть

$$A = \begin{pmatrix} a & b \\ c & d \end{pmatrix}$$

Обратная матрица находится по следующему правилу:

а) Поменять местами элементы главной диагонали
б) Изменить знаки у элементов побочной диагонали
в) Разделить полученную матрицу на определитель $\det A = ad - bc$

В результате:

$$A^{-1} = \frac{1}{ad - bc} \begin{pmatrix} d & -b \\ -c & a \end{pmatrix} \tag{4.2}$$

Пояснение:

$$\begin{aligned} \bold{1.}~ & \det A = ad - bc; \\[5pt] \bold{2.}~ & \begin{pmatrix} A_{ij} \end{pmatrix} = \begin{pmatrix} d & -c \\ -b & a \end{pmatrix}; \\[5pt] \bold{3.}~ & A^{+} = \begin{pmatrix} d & -b \\ -c & a \end{pmatrix}; \\[5pt] \bold{4.}~ & A^{-1} = \frac{1}{ad - bc} \begin{pmatrix} d & -b \\ -c & a \end{pmatrix} \end{aligned}$$

2. Альтернативная реализация второго способа (по столбцам)

1. Составить блочную матрицу:

$$\left( \frac{A}{E} \right)$$

1. При помощи элементарных преобразований столбцов привести её к виду:

$$\left( \frac{E}{T} \right)$$

Тогда блок T будет равен:

$$T = A^{-1}$$

Матричные уравнения

Рассмотрим матричное уравнение вида

$$A \cdot X = B \tag{4.5}$$

где $A$ и $B$ — данные матрицы, имеющие одинаковое количество строк, причем матрица $A$ квадратная. Требуется найти матрицу $X$, удовлетворяющую уравнению.

О существовании и единственности решения матричного уравнения (4.5):
Если определитель матрицы $A$ отличен от нуля, то матричное уравнение (4.5) имеет единственное решение
$$X = A^{-1} B$$

В самом деле, подставляя $X = A^{-1} B$ в левую часть (4.5), получаем:
$$A (A^{-1} B) = \underbrace{A A^{-1}}_{E} B = B,$$
т.е. правую часть уравнения.

Заметим, что решением уравнения $A X = E$ является обратная матрица: $X = A^{-1}$.

---

Рассмотрим также уравнение вида

$$Y \cdot A = B \tag$$

где $A$ и $B$ — данные матрицы, имеющие одинаковое количество столбцов, и $A$ — квадратная.

---

Теорема О существовании и единственности решения уравнения

Если $\det A \ne 0$, то имеет единственное решение
$$Y = B A^{-1}$$

---

Заметим:
- В уравнении матрица $X$ умножается на $A$ слева — это "левое частное".
- В уравнении матрица $Y$ умножается на $A$ справа — это "правое частное".

---

Пример

Даны матрицы:

$$A = \begin{pmatrix}1 & 2 \\ 1 & 4\end{pmatrix}, \quad B = \begin{pmatrix}1 & 3 & 5 \\ 2 & 4 & 6\end{pmatrix}, \quad C = \begin{pmatrix}1 & 2 \\ 3 & 4 \\ 5 & 6\end{pmatrix}$$

Обратная матрица:

$$A^{-1} = \begin{pmatrix}2 & -1 \\ -\tfrac{1}{2} & \tfrac{1}{2}\end{pmatrix}$$

---

а) Решить $AX = B$

$$X = A^{-1} B = \begin{pmatrix}2 & -1 \\ -\tfrac{1}{2} & \tfrac{1}{2}\end{pmatrix} \cdot \begin{pmatrix}1 & 3 & 5 \\ 2 & 4 & 6\end{pmatrix} = \begin{pmatrix}0 & 2 & 4 \\ \tfrac{1}{2} & \tfrac{1}{2} & \tfrac{1}{2} \end{pmatrix}$$

---

б) Уравнение $YB = B$

Решений нет, так как количество столбцов у $B$ — 3, а у $A$ — 2. Размеры не согласованы.

---

в) Решить $YA = C$

$$Y = C A^{-1} = \begin{pmatrix}1 & 2 \\ 3 & 4 \\ 5 & 6\end{pmatrix} \cdot \begin{pmatrix}2 & -1 \\ -\tfrac{1}{2} & \tfrac{1}{2} \end{pmatrix} = \begin{pmatrix}1 & 0 \\ 4 & -1 \\ 7 & -2\end{pmatrix}$$

---

Пример

Решить уравнение:
$$BX + 2X = E, \quad \text{где } B = \begin{pmatrix}-1 & 2 \\ 1 & 2\end{pmatrix}$$

Решение.
Преобразуем:
$$BX + 2X = BX + 2EX = (B + 2E)X$$

где
$$E = \begin{pmatrix}1 & 0 \\ 0 & 1\end{pmatrix}, \quad A = B + 2E = \begin{pmatrix}-1 & 2 \\ 1 & 2\end{pmatrix} + \begin{pmatrix}2 & 0 \\ 0 & 2\end{pmatrix} = \begin{pmatrix}1 & 2 \\ 1 & 4\end{pmatrix}$$

$$X = A^{-1} E = A^{-1} = \begin{pmatrix}2 & -1 \\ -\tfrac{1}{2} & \tfrac{1}{2} \end{pmatrix}$$

Псевдообратная матрица

Обратная матрица в отличие от полуобратной имеет в силу определения очевидные свойства:

$$\begin{pmatrix}A\cdot A^{-1}\end{pmatrix}^{\ast}=A\cdot A^{-1},\qquad \begin{pmatrix}A^{-1}\cdot A\end{pmatrix}^{\ast}=A^{-1}\cdot A,$$

так как единичная матрица $E=AA^{-1}=A^{-1}A$, разумеется, эрмитова. В определении полуобратной матрицы имеется некоторый произвол (см. п.3 замечаний 4.6), которым можно воспользоваться так, чтобы полуобратная матрица обладала аналогичными свойствами.

Пусть $A$ — произвольная матрица размеров $m\times n$. Полуобратная матрица $A^{\sim1}$ размеров $n\times m$ называется псевдообратной для матрицы $A$, если матрицы $AA^{\sim1}$ и $A^{\sim1}A$ эрмитовы, т.е. псевдообратная матрица $A^{\sim1}$ определяется четырьмя условиями:

$$AA^{\sim1}A=A;\qquad A^{\sim1}AA^{\sim1}=A^{\sim1}; \tag{4.17}$$

$$\begin{pmatrix}AA^{\sim1}\end{pmatrix}^{\ast}=AA^{\ast};\qquad \begin{pmatrix}A^{\sim1}A\end{pmatrix}^{\ast}=A^{\sim1}A. \tag{4.18}$$

Покажем, что псевдообратная матрица $A^{\sim1}$ существует для любой матрицы $A$. Действительно, если $A=O$ — нулевая матрица размеров $m\times n$, то $A^{\sim1}=O^T$ — нулевая размеров $n\times m$, что следует из равенств (4.17).

Пусть матрица $A$ — ненулевая. Тогда матрица $A^{\sim1}$, удовлетворяющая равенствам (4.17), имеет вид (4.14):

$$A^{\sim1}=T\cdot\! \begin{pmatrix}\dfrac{E_r}{U}\end{pmatrix}\!\cdot\! \begin{pmatrix}E_r\mid V\end{pmatrix}\!\cdot S. \tag{4.19}$$

Покажем, что выбором матриц $U$ и $V$ в формуле (4.19) можно получить матрицу, удовлетворяющую условиям (4.18). В самом деле, запишем скелетное разложение (4.10) матрицы $A$:

$$A=S^{-1}\Lambda T^{-1}= S^{-1}\! \begin{pmatrix}E_r\!\!&\vline\!\!&O\\\hline O\!\!&\vline\!\!&O\end{pmatrix}\!T^{-1}= S^{-1}\cdot\! \begin{pmatrix}\dfrac{E_r}{O} \end{pmatrix}\!\cdot\! \begin{pmatrix}E_r\mid O\end{pmatrix}\!\cdot T^{-1}.$$

Найдем произведение:

$$\begin{gathered}AA^{-1}= S^{-1}\cdot\!\begin{pmatrix} \dfrac{E_r}{O} \end{pmatrix}\!\cdot\! \begin{pmatrix}E_r\mid O\end{pmatrix}\!\cdot\underbrace{T^{-1}\cdot T}_{E_n}\cdot\! \begin{pmatrix}\dfrac{E_r}{U} \end{pmatrix}\!\cdot\! \begin{pmatrix}E_r\mid U\end{pmatrix}\!\cdot S=\\[2pt] =S^{-1}\cdot\! \begin{pmatrix}\dfrac{E_r}{O}\end{pmatrix}\!\cdot \underbrace{\begin{pmatrix}E_r\mid O\end{pmatrix}\!\cdot \begin{pmatrix}\dfrac{E_r}{U} \end{pmatrix}}_{E_r}\cdot\! \begin{pmatrix} E_r\mid V\end{pmatrix}\!\cdot S=S^{-1}\cdot\! \begin{pmatrix}\dfrac{E_r}{O} \end{pmatrix}\!\cdot\! \begin{pmatrix}E_r\mid V\end{pmatrix}\!\cdot S= S^{-1}\cdot\! \begin{pmatrix} E_r\!\!&\vline\!\!&V\\ \hline O\!\!&\vline\!\!& O\end{pmatrix}\!\cdot S.\end{gathered}$$

Подставим его в первое из равенств (4.18):

$$\left[S^{-1}\cdot\! \begin{pmatrix}E_r\!\!&\vline\!\!&V\\ \hline O\!\!&\vline\!\!& O\end{pmatrix}\!\cdot S\right]^{\ast}= S^{-1}\cdot\! \begin{pmatrix}E_r\!\!&\vline\!\!&V\\ \hline O\!\!&\vline\!\!& O\end{pmatrix}\!\cdot S.$$

Используя свойства операции сопряжения, а также п. 1 замечаний 4.2, получаем:

$$S^{\ast}\cdot\! \begin{pmatrix} E_r\!\!&\vline\!\!&O\\ \hline V^{\ast}\!\!&\vline\!\!& O \end{pmatrix}\!\cdot\! \begin{pmatrix}S^{-1}\end{pmatrix}^{\ast}= S^{-1}\cdot\! \begin{pmatrix} E_r\!\!&\vline\!\!&V\\ \hline O\!\!&\vline\!\!& O \end{pmatrix}\!\cdot S.$$

Умножая обе части равенства на матрицу $S$ слева и на матрицу $S^{\ast}$ справа, приходим к равенству:

$$\begin{pmatrix}SS^{\ast}\end{pmatrix}\!\cdot\! \begin{pmatrix} E_r\!\!&\vline\!\!&O\\ \hline V^{\ast}\!\!&\vline\!\!& O \end{pmatrix}= \begin{pmatrix} E_r\!\!&\vline\!\!&V\\ \hline O\!\!&\vline\!\!& O \end{pmatrix}\!\cdot\! \begin{pmatrix}SS^{\ast}\end{pmatrix}\!.$$

Подставим в это равенство матрицу $SS^{\ast}$, предварительно разбив ее на блоки $SS^{\ast}=\begin{pmatrix} S_1\!\!&\vline\!\!&S_2\\ \hline S_3\!\!&\vline\!\!& S_4 \end{pmatrix}$ квадратными матрицами $S_1$ и $S_4$ порядков $r$ и $(m-r)$ и прямоугольными матрицами $S_2$ и $S_2$ размеров $r\times(m-r)$ и $(m-r)\times r$ соответственно. Выполняя умножение блочных матриц, получаем:

$$\begin{gathered} \begin{pmatrix} S_1\!\!&\vline\!\!&S_2\\ \hline S_3\!\!&\vline\!\!& S_4\end{pmatrix}\!\cdot\! \begin{pmatrix} E_r\!\!&\vline\!\!&O\\ \hline V^{\ast}\!\!&\vline\!\!& O\end{pmatrix}= \begin{pmatrix} S_1+S_2V^{\ast}\!\!&\vline\!\!&O\\ \hline S_3+S_4V^{\ast}\!\!&\vline\!\!& O\end{pmatrix}\!,\\[2pt] \begin{pmatrix} E_r\!\!&\vline\!\!&V\\ \hline O\!\!&\vline\!\!& O\end{pmatrix}\!\cdot\! \begin{pmatrix} S_1\!\!&\vline\!\!&S_2\\ \hline S_3\!\!&\vline\!\!& S_4\end{pmatrix}= \begin{pmatrix} S_1+VS_3\!\!&\vline\!\!&S_2+VS_4\\ \hline O\!\!&\vline\!\!& O\end{pmatrix}\!.\end{gathered}$$

Равенство полученных блочных матриц обеспечивается условием:

$$V=-S_2S_{4}^{-1}, \text{ поскольку } S_3=S_2^{\ast},~S_1=S_1^{\ast},~ S_4=S_4^{\ast}$$

в силу эрмитовости матрицы $SS^{\ast}$, а $\begin{pmatrix}S_4^{-1}\end{pmatrix}^{\ast}= \begin{pmatrix}S_4^{\ast}\end{pmatrix}^{-1}$.

Аналогичным образом можно показать, что второе из равенств (4.18) выполняется, если положить:

$$U=-T_4^{-1}T_3,$$

где $T_3,T_4$ — блоки размеров $(n-r)\times r$ и $(n-r)\times(n-r)$ матрицы $T^{\ast}T=\begin{pmatrix} T_1\!\!&\vline\!\!&T_2\\ \hline T_3\!\!&\vline\!\!& T_4\end{pmatrix}$.

Таким образом, для любой матрицы существует псевдообратная матрица и притом только одна.

Замечания 4.7

1. Если матрица $A$ обратимая, то обратная матрица $A^{-1}$, как следует из п. 1 замечаний 4.6, совпадает с псевдообратной, т.е. $A^{-1}=A^{\sim1}$.

2. Из невырожденности матриц $S$ и $T$ следует, что при любом разбиении эрмитовых матриц:

$$SS^{\ast}=\begin{pmatrix} S_1\!\!&\vline\!\!&S_2\\ \hline S_3\!\!&\vline\!\!& S_4\end{pmatrix},\qquad T^{\ast}T=\begin{pmatrix} T_1\!\!&\vline\!\!&T_2\\ \hline T_3\!\!&\vline\!\!& T_4\end{pmatrix}\!,$$

на квадратные блоки $S_1,\,S_4,\,T_1,\,T_4$, существуют обратные матрицы $S_1^{-1},\,S_4^{-1},\,T_1^{-1},\,T_4^{-1}$.

1. Имеются другие определения псевдообратной матрицы, равносильные приведенному выше. Например:

$$A^{\sim1}= \lim_{\varepsilon\to0}\Bigl(A^{\ast}A+\varepsilon^2\cdot E\Bigr)^{-1}A^{\ast}= \lim_{\varepsilon\to0}A^{\ast}\Bigl(A^{\ast}A+\varepsilon^2\cdot E\Bigr)^{-1}.$$

1. В общем случае произведение псевдообратных матриц некоммутативно $(AB)^{\sim1}\ne B^{\sim1}\cdot A^{\sim1}$.

Свойства псевдообратной матрицы

Операция псевдообращения матриц обладает следующими свойствами:

$$\begin{aligned} \bold{1.}&~~ (A^{\sim1})^{\sim1}=A;\\[2pt] \bold{2.}&~~ (A^{\ast})^{\sim1}=(A^{\sim1})^{\ast};\\[2pt] \bold{3.}&~~ A^{\sim1}=(A^{\ast}A)^{\sim1}A^{\ast}=A^{\ast}(AA^{\ast})^{\sim1};\\[2pt] \bold{4.}&~~ (AA^{\sim1})^2=AA^{\sim1};\\[2pt] \bold{5.}&~~ (A^{\sim1}A)^2=A^{\sim1}A. \end{aligned}$$

Эти свойства доказываются по определению (4.17), (4.18). Докажем, например, свойство 3 (первое равенство). По определению псевдообратной матрицы имеем:

$$\Bigl[(A^{\ast}A)^{\sim1}A^{\ast}\Bigr]\cdot A\cdot\Bigl[(A^{\ast}A)^{\sim1}A^{\ast}\Bigr]= (A^{\ast}A)^{\sim1}\cdot(A^{\ast}A)\cdot(A^{\ast}A)^{\sim1}A^{\ast}= (A^{\ast}A)^{\sim1}A^{\ast}.$$

Следовательно, $A=\bigl[(A^{\ast}A)^{\sim1}A^{\ast}\bigr]^{\sim1}$. Тогда по свойству 1: $A^{\sim1}=(A^{\ast}A)^{\sim1}A^{\ast}$.

Способы нахождения псевдообратной матрицы

Пусть дана ненулевая матрица $A$ размеров $m \times n$. Требуется найти псевдообратную матрицу $A^{\sim 1}$.

Первый способ

Для нахождения псевдообратной матрицы (4.19) нужно выполнить следующие действия:

1. Составить блочную матрицу
   $$\begin{pmatrix}A\!\!&\vline\!\!&E_m\\\hline E_n\!\!&\vline\!\!&{} \end{pmatrix},$$
   приписывая к матрице $A$ слева и снизу единичные матрицы соответствующих размеров. Правый нижний блок этой матрицы может быть произвольным.

2. Элементарными преобразованиями над первыми $m$ строками и первыми $n$ столбцами привести блочную матрицу к виду
   $$\begin{pmatrix}\Lambda\!\!& \vline\!\!&S\\\hline T\!\!&\vline\!\!&{}\end{pmatrix},$$
   где $\Lambda$ — матрица простейшего вида (4.8):
   $$\Lambda=\begin{pmatrix} E_r\!\!&\vline\!\!&O\\\hline O\!\!&\vline\!\!&O\end{pmatrix},$$
   где $E_r$ — единичная матрица порядка $r$ ($1 \leqslant r \leqslant \min\{m,n\}$).

3. Найти произведения $SS^{\ast}$ и $T^{\ast}T$, представив их в виде блочных матриц:
   $$SS^{\ast}=\begin{pmatrix}S_1\!\!&\vline\!\!&S_2\\\hline S_3\!\!&\vline\!\!&S_4\end{pmatrix}\!,\quad T^{\ast}T=\begin{pmatrix}T_1\!\!&\vline\!\!&T_2\\\hline T_3\!\!&\vline\!\!&T_4\end{pmatrix}\!,\tag{4.20}$$
   выделяя блоки $S_2, S_4$ размеров $r \times (m-r)$, $(m-r) \times (m-r)$ и $T_3, T_4$ размеров $(n-r) \times r$, $(n-r) \times (n-r)$.

4. Вычислить матрицы:
   $$U=-T_4^{-1}T_3,\quad V=-S_2S_4^{-1}.$$

5. Получить псевдообратную матрицу:
   $$A^{\sim1}=T\cdot\! \begin{pmatrix}\dfrac{E_r}{U}\end{pmatrix}\!\cdot\! \begin{pmatrix}E_r\mid V\end{pmatrix}\!\cdot S.\tag{4.21}$$

Замечание 4.8. Если $r = m$ или $r = n$, в (4.20) будут отсутствовать соответствующие блоки. В частных случаях, когда строки или столбцы матрицы $A$ линейно независимы, псевдообратную матрицу можно найти проще (см. далее частные случаи).

Второй способ

Используем скелетное разложение (4.10):

1-2. Выполнить первые два пункта первого способа. Получить матрицы $S, T$ и $\Lambda$, удовлетворяющие условию:
$$\Lambda = S \cdot A \cdot T,$$
где $\Lambda = \begin{pmatrix}E_r\!\!&\vline\!\!&O\\\hline O\!\!&\vline\!\!&O\end{pmatrix}$.

1. Найти обратные матрицы $S^{-1}$ и $T^{-1}$.

2. Записать матрицы:
   $$B = S^{-1} \cdot \begin{pmatrix}\dfrac{E_r}{O}\end{pmatrix}, \quad C = \begin{pmatrix}E_r \mid O\end{pmatrix} \cdot T^{-1}.$$
   Матрица $B$ состоит из первых $r$ столбцов $S^{-1}$, а $C$ — из первых $r$ строк $T^{-1}$.

3. Получить псевдообратную матрицу по формуле:
   $$A^{\sim1} = C^{\ast} \cdot (CC^{\ast})^{-1} \cdot (B^{\ast}B)^{-1} \cdot B^{\ast}.\tag{4.22}$$

Доказательство эквивалентности способов:

Имея скелетное разложение $A = BC$, найдем:
$$\begin{aligned} (B^{\ast}B)^{-1}B^{\ast}S^{-1} &= \left[\begin{pmatrix}E_r & \mid O\end{pmatrix}(S^{-1})^{\ast}S^{-1}\begin{pmatrix}\dfrac{E_r}{O}\end{pmatrix}\right]^{-1}\begin{pmatrix}E_r \mid O\end{pmatrix}(S^{-1})^{\ast}S^{-1} \\ &= \left[\begin{pmatrix}E_r \mid O\end{pmatrix}(SS^{\ast})^{-1}\begin{pmatrix}\dfrac{E_r}{O}\end{pmatrix}\right]^{-1}\begin{pmatrix}E_r \mid O\end{pmatrix}(SS^{\ast})^{-1} \end{aligned}$$

Обращая блочную матрицу $SS^{\ast}$ по формуле Фробениуса:
$$\begin{pmatrix}S_1\!\!&\vline\!\!&S_2\\\hline S_3\!\!&\vline\!\!&S_4\end{pmatrix}^{-1}= \begin{pmatrix} M\!\!&\vline\!\!&-MS_2S_4^{-1}\\\hline -S_4^{-1}S_3M\!\!& \vline\!\!&N \end{pmatrix}\!,$$
где $M = (S_1 - S_2S_4^{-1}S_3)^{-1}$, получаем:
$$(B^{\ast}B)^{-1}B^{\ast}S^{-1} = \begin{pmatrix}E_r \mid V\end{pmatrix}S,$$
где $V = -S_2S_4^{-1}$. Аналогично для второго множителя. Таким образом, формулы (4.22) и (4.21) дают одинаковый результат.

Частные случаи нахождения псевдообратной матрицы

1. Скалярный случай

Если матрица $A = (a_{11})$ - число:
$$A^{\sim1} = \begin{cases} \dfrac{1}{a_{11}}, & a_{11} \ne 0, \\ 0, & a_{11} = 0. \end{cases}$$

2. Диагональная матрица

Для $A = \operatorname{diag}(a_{11}, a_{22}, \ldots, a_{nn})$:
$$A^{\sim1} = \operatorname{diag}(a_{11}^{-1}, a_{22}^{-1}, \ldots, a_{nn}^{-1}),$$
где
$$a_{ii}^{-1} = \begin{cases} \dfrac{1}{a_{ii}}, & a_{ii} \ne 0, \\ 0, & a_{ii} = 0, \end{cases} \quad i = 1,2,\ldots,n. \tag{4.23}$$

3. Линейно независимые столбцы

Если столбцы $A$ линейно независимы:
$$A^{\sim1} = (A^{\ast}A)^{-1}A^{\ast}. \tag{4.24}$$

4. Линейно независимые строки

Если строки $A$ линейно независимы:
$$A^{\sim1} = A^{\ast}(AA^{\ast})^{-1}. \tag{4.25}$$

Пример

Найти псевдообратные матрицы для:
$$A = \begin{pmatrix}1&0&0\\0&2&0\\0&0&0\end{pmatrix}, \quad B = \begin{pmatrix}1&2&3\end{pmatrix}, \quad C = \begin{pmatrix}1&0\\1&1\\1&1\end{pmatrix}.$$

Решение

Для матрицы $A$ (диагональная):
$$A^{\sim1} = \begin{pmatrix}1&0&0\\0&1/2&0\\0&0&0\end{pmatrix}.$$

Для матрицы $B$ (матрица-строка):
$$B^{\sim1} = \begin{pmatrix}1\\2\\3\end{pmatrix} \cdot \left[\begin{pmatrix}1&2&3\end{pmatrix} \begin{pmatrix}1\\2\\3\end{pmatrix}\right]^{-1} = \frac{1}{14}\begin{pmatrix}1\\2\\3\end{pmatrix}.$$

Для матрицы $C$ (линейно независимые столбцы):
$$\begin{aligned} C^{\sim1} &= \left[\begin{pmatrix}1&1&1\\0&1&1\end{pmatrix} \begin{pmatrix}1&0\\1&1\\1&1\end{pmatrix}\right]^{-1} \begin{pmatrix}1&1&1\\0&1&1\end{pmatrix} \\ &= \begin{pmatrix}3&2\\2&2\end{pmatrix}^{-1} \begin{pmatrix}1&1&1\\0&1&1\end{pmatrix} \\ &= \frac{1}{2}\begin{pmatrix}2&-2\\-2&3\end{pmatrix} \begin{pmatrix}1&1&1\\0&1&1\end{pmatrix} \\ &= \begin{pmatrix}1&0&0\\-1&1/2&1/2\end{pmatrix}. \end{aligned}$$

Проверка первым способом:

1. Составляем блочную матрицу:
   $$\begin{pmatrix}C & \vline & E_3 \\ \hline E_2 & \vline & {}\end{pmatrix} = \begin{pmatrix}1&0 & \vline & 1&0&0 \\ 1&1 & \vline & 0&1&0 \\ 1&1 & \vline & 0&0&1 \\ \hline 1&0 & \vline & {}&{}&{} \\ 0&1 & \vline & {}&{}&{}\end{pmatrix}$$

2. Приводим к ступенчатому виду:
   $$\sim \begin{pmatrix}1&0 & \vline & 1&0&0 \\ 0&1 & \vline & -1&1&0 \\ 0&0 & \vline & 0&-1&1 \\ \hline 1&0 & \vline & {}&{}&{} \\ 0&1 & \vline & {}&{}&{}\end{pmatrix}$$

Получаем $T = E_2$, $S = \begin{pmatrix}1&0&0\\-1&1&0\\0&-1&1\end{pmatrix}$, $r = 2$.

1. Находим:
   $$SS^{\ast} = \begin{pmatrix}1&-1&0\\-1&2&-1\\0&-1&2\end{pmatrix} = \begin{pmatrix}S_1 & \vline & S_2 \\ \hline S_3 & \vline & S_4\end{pmatrix}$$
   $$V = -S_2S_4^{-1} = \begin{pmatrix}0\\1/2\end{pmatrix}$$

2. Итоговая псевдообратная матрица:
   $$C^{\sim1} = \begin{pmatrix}1&0&0\\-1&1/2&1/2\end{pmatrix}$$
   Результаты обоих методов совпадают.

Метод наименьших квадратов в матричном виде (МНК)

Представим данные как систему линейных уравнений.

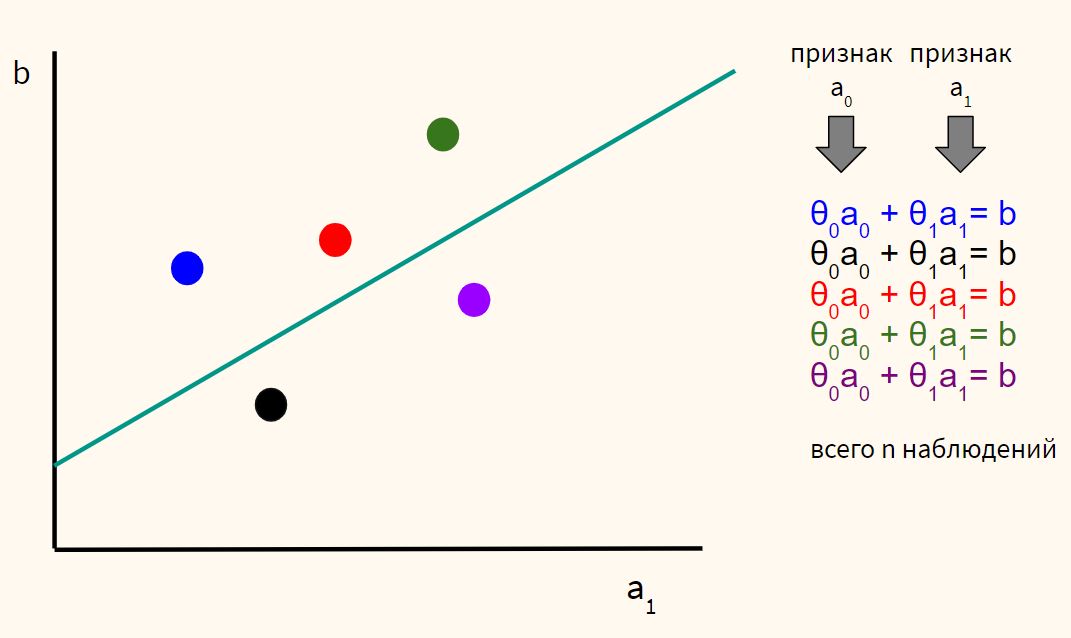
Выше обычная задача простой линейной регрессии с немного измененной нотацией. У нас есть пять наблюдений (для каждого наблюдения есть информация $a_0$ и $a_1$, $a_0$ заполнена единицами). Подставив некоторые веса $\theta_0$ и $\theta_1$, мы получим для каждой точки некоторую целевую переменную $b$ (обычно мы её обозначали через $y$).

Единственного решения для такой системы не существует, то есть мы не сможем подобрать такие $\theta_0$ и $\theta_1$, которые бы удовлетворяли всем $a_0$ и $a_1$ в каждой строке (для каждого из наблюдений).

Такая система уравнений называется переопределенной (overdetermined). У нас пять уравнений (наблюдений) и при двух неизвестных (коэффициентах). Можно также сказать, что мы наложили слишком много ограничений (ограничения, в данном случае, это уравнения), чтобы найти единственное решение.

Перепишем эту систему с помощью матриц. В общем случае у нас, конечно, может быть больше признаков $a_0, a_1, a_2, \dots, a_k$, однако систему по-прежнему будем считать переопределенной, то есть $n > k$. Также заменим $\theta$ на $x$.

$$\begin{bmatrix} \vdots & \vdots & \vdots & \vdots \\ a_1 & a_2 & \dots & a_k \\ \vdots & \vdots & \vdots & \vdots \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_k \end{bmatrix} = \begin{bmatrix} b_1 \\ b_2 \\ \vdots \\ b_n \end{bmatrix}$$

$$\underset{n \times k}{A} \mathbf{x} = \mathbf{b}$$

При этом в данном случае $A, \mathbf{x} \in \mathbb{R}^k$, а $\mathbf{b} \in \mathbb{R}^n$. То есть вектор $\mathbf{b}$ находится в пространстве большей размерности, чем $\mathbf{x}$. Например, вектор $\mathbf{x}$ может находиться на плоскости (двумерный вектор), а вектор $\mathbf{b}$ — в трехмерном пространстве.

Можно также сказать, что не существует линейной комбинации значений вектора $\mathbf{x}$ (веса модели) и векторов $a_0, a_1, a_2, \dots, a_k$, которые преобразовывались бы в вектор $\mathbf{b}$.

$$x_1 \mathbf{a}_1 + x_2 \mathbf{a}_2 + x_3 \mathbf{a}_3 + \dots + x_k \mathbf{a}_k \neq \mathbf{b}$$

Наконец, справедливо, что $\mathbf{b}$ не находится в пространстве столбцов $A$, $\mathbf{b} \notin \text{col}(A)$ (то есть не находится на плоскости), а вектор $\mathbf{x}$ как раз лежит на этой плоскости, и это значит, что мы никак не можем перевести с помощью матрицы $A$ вектор $\mathbf{x}$ из двумерного пространства в трехмерное.

С другой стороны, мы можем попробовать получить наилучшее возможное решение, найдя такой вектор $\mathbf{x}^*$, который будет максимально приближен к вектору $\mathbf{b}$ (т.е. будет иметь минимальное расстояние до него). Расстояние же между векторами можно определить как разницу двух векторов.

Для того чтобы положительные и отрицательные значения не взаимоудалялись, возведем значения в квадрат.

$$\min \|\mathbf{b} - A \mathbf{x}^*\|^2$$

Очевидно, что вектор (назовем его $\mathbf{p}$), получившийся в результате $A \mathbf{x}^*$, будет в пространстве $\mathbb{R}^k$, что то же самое, что $\mathbf{p} \in \text{col}(A)$ (то есть в данном случае на плоскости).

Далее, наименьшее расстояние от вектора $\mathbf{b}$ до $\mathbf{p}$ можно определить как ортогональную проекцию $\mathbf{b}$ на пространство столбцов $A$.

$$A \mathbf{x}^* = \mathbf{p} = \text{proj}_{\text{col}(A)} \mathbf{b}$$

Попробуем найти решение относительно $\mathbf{b}$.

$$A \mathbf{x}^* = \text{proj}_{\text{col}(A)} \mathbf{b}$$

Вычтем вектор $\mathbf{b}$ из обеих частей.

$$A \mathbf{x}^* - \mathbf{b} = \text{proj}_{\text{col}(A)} \mathbf{b} - \mathbf{b}$$

Заметим, что вектор $\text{proj}_{\text{col}(A)} \mathbf{b} - \mathbf{b}$ (на рисунке представлен красным вектором) ортогонален к плоскости $\text{col}(A)$. Как следствие, $A \mathbf{x}^* - \mathbf{b}$ ортогонально $\text{col}(A)$.

Можно также сказать, что $A \mathbf{x}^* - \mathbf{b}$ является ортогональным дополнением пространства $\text{col}(A)$. Запишем это как $A \mathbf{x}^* - \mathbf{b} = \text{col}(A)^{\perp}$.

Одновременно ортогональное дополнение пространства столбцов матрицы $A$ равно ядру $A^\top$, то есть $\text{col}(A)^{\perp} = \text{null}(A^\top)$. Тогда:

$$A \mathbf{x}^* - \mathbf{b} \in \text{null}(A^{T})$$

Если умножить матрицу $A^\top$ на её ядро $A \mathbf{x}^* - \mathbf{b}$, то мы получим нулевой вектор.

$$A^\top (A \mathbf{x}^* - \mathbf{b}) = \mathbf{0}$$

$$A^\top A \mathbf{x}^* - A^\top \mathbf{b} = \mathbf{0}$$

$$A^\top A \mathbf{x}^* = A^\top \mathbf{b}$$

Таким образом, можно найти $\mathbf{x}^*$, которое минимизирует квадрат расстояния между вектором $\mathbf{b}$ и вектором проекции $A \mathbf{x}^*$.

---

Уверен, вы узнали в этом выражении нормальные уравнения, о которых мы говорили на занятии по линейной регрессии.

$$X^\top X\theta = X^\top y$$

Нормальными же эти уравнения называются, потому что $A \mathbf{x}^* - \mathbf{b} \perp \text{col}(A)$, а нормалью в геометрии как раз считается обобщенное понятие перпендикуляра к поверхности.

---

Более того, можно сказать, что минимизация расстояний от точек до прямой вдоль оси $y$ одновременно приводит к минимизации длины перпендикуляров к проекциям точек.

Благодарности && использованные источники

1. Записная книжка УТЕШЕВА Алексея Юрьевича
2. Математический форум Math Help Planet
3. Дмитрий Макаров. Метод наименьших квадратов