Лекция 4 Линейное отображение. Линейный Оператор. Матрица линейного оператора.

Презентация доступна здесь

Линейным отображением линейного векторного пространства $V$ с операцией сложения векторов, обозначаемой $+$, в линейное векторное пространство $W$ с операцией сложения векторов, обозначаемой $\oplus$, называется функция (соответствие) $A: V \longrightarrow W$ (т.е. определенная на $V$, имеющая значения в $W$), обладающая свойством линейности, которое описывается одним из двух эквивалентных представлений:

1. $A(X_1 + X_2) = A(X_1) \oplus A(X_2)$,
2. $A(\alpha_1 X_1) = \alpha_1 A(X_1)$,
   или
3. $A(\alpha_1 X_1 + \alpha_2 X_2) = \alpha_1 A(X_1) \oplus \alpha_2 A(X_2)$.

Указанные свойства должны быть выполнены для любых векторов $X_1, X_2$ пространства $V$ и любых скаляров $\alpha_1, \alpha_2$ (вещественных, если оба пространства вещественны, и комплексных, если хотя бы одно из пространств комплексное).

Если $Y = A(X)$, то говорят, что $Y$ — образ вектора $X$, а $X$ — прообраз вектора $Y$ при отображении $A$. Пространство $V$ называется областью определения отображения $A$.

Tip

Образно говоря, свойство линейности отображения заключается в том, что при этом отображении образ суммы любых двух векторов совпадает с суммой образов этих векторов, а произвольное растяжение прообраза влечет за собой сообразное же растяжение образа

Примеры линейных отображений

Пример 1. Рассмотрим линейное пространство полиномов степени не выше $n$:

$$P_n = \{ p(x) \in \mathbb{R}[x] \mid \deg p(x) \leq n \};$$

в это же множество включаем и тождественно нулевой полином (для которого степень не определяется). Операция нахождения частного и операция нахождения остатка от деления полинома $p(x)$ на заданный фиксированный полином $g(x) \in \mathbb{R}[x]$, $g(x) \neq 0$, являются линейными отображениями пространства $P_n$. Если

$$p_1(x) \equiv q_1(x) g(x) + r_1(x),$$

$$p_2(x) \equiv q_2(x) g(x) + r_2(x),$$

при $\deg r_j(x) < \deg g(x)$, то

$$(\alpha_1 p_1(x) + \alpha_2 p_2(x)) \equiv (\alpha_1 q_1(x) + \alpha_2 q_2(x)) g(x) + (\alpha_1 r_1(x) + \alpha_2 r_2(x)).$$

Фактически, операция деления на $g(x)$ (с остатком) порождает два разных линейных отображения. Если $\deg g(x) = m$ при $0 < m \leq n$, то операция нахождения остатка — это отображение $P_n \longrightarrow P_{m-1}$, а операция нахождения частного — это

Пример 2. В том же линейном пространстве $P_n$ операция дифференцирования

$$\frac{d}{dx}: p(x) \longmapsto p'(x)$$

является отображением $P_n$ в $P_{n-1}$, линейным, поскольку

$$\frac{d}{dx}(\alpha_1 p_1(x) + \alpha_2 p_2(x)) = \alpha_1 \frac{d}{dx} p_1(x) + \alpha_2 \frac{d}{dx} p_2(x).$$

Прообраз любого элемента $P_{n-1}$ неединствен:

$$\frac{d}{dx} \left( \frac{1}{2} x^2 + \text{const} \right) = x.$$

Пример 3. Операцию нахождения первообразной:

$$\int_0^x p(t) \, dt: p(x) \longmapsto \int_0^x p(t) \, dt$$

$a_0 x^n + a_1 x^{n-1} + \dots + a_n \longmapsto \frac{a_0}{n+1} x^{n+1} + \frac{a_1}{n} x^n + \dots + a_n x$

тоже можно рассматривать как линейное отображение $P_n \longrightarrow P_{n+1}$. При этом прообраз каждого полинома из $P_{n+1}$ (если существует) будет единствен.

Пример 4. Рассмотрим линейное отображение $\mathbb{R}^3 \longrightarrow \mathbb{R}^3$:

$$\begin{pmatrix} x \\ y \\ z \end{pmatrix} \longmapsto \begin{pmatrix} x \\ y \\ 0 \end{pmatrix}$$

задает ортогональную проекцию вектора $X = (x, y, z)$ на плоскость $z = 0$. Можно рассматривать его и как отображение $\mathbb{R}^3 \longrightarrow \mathbb{R}^2$.

Проецирование же на произвольное подпространство может быть задано с помощью матрицы. Так, например, отображение

$$\begin{pmatrix} x \\ y \\ z \end{pmatrix} \longmapsto \frac{1}{3} \begin{pmatrix} 2 & -1 & -1 \\ -1 & 2 & -1 \\ -1 & -1 & 2 \end{pmatrix} \begin{pmatrix} x \\ y \\ z \end{pmatrix}$$

задает ортогональную проекцию вектора $X$ на многообразие $x + y + z = 0$.

Свойства линейных отображений

В настоящем пункте $O$ означает нулевой вектор пространства $V$, а $O'$ — нулевой вектор пространства $W$.

Два линейных отображения $A$ и $B$ из $V$ в $W$ называются равными, если $A(X) = B(X)$ для любого $X \in V$. Нулевое отображение определяется условием $O(X) = O'$ для всех $X \in V$.

Теорема 1. Для любого линейного отображения $A(X)$:

• а) $A(O) = O'$;
• б) если система $\{X_1, \dots, X_k\}$ линейно зависима, то и система $\{A(X_1), \dots, A(X_k)\}$ линейно зависима;
• в) если система $\{A(X_1), \dots, A(X_k)\}$ линейно независима, то и система $\{X_1, \dots, X_k\}$ линейно независима.

Теорема 2. Линейное отображение отображает произвольное линейное многообразие пространства $V$ в линейное же многообразие пространства $W$.

Доказательство: Если $M = X_0 + L(X_1, \dots, X_k) = \{ X_0 + \alpha_1 X_1 + \dots + \alpha_k X_k \mid (\alpha_1, \dots, \alpha_k) \in \mathbb{R}^k \}$, то свойство линейности отображения $A$ дает:

$$A(M) = \{ A(X_0) \oplus \alpha_1 A(X_1) \oplus \dots \oplus \alpha_k A(X_k) \mid (\alpha_1, \dots, \alpha_k) \in \mathbb{R}^k \} = A(X_0) \oplus L(A(X_1), \dots, A(X_k))$$

Заметим, что в соответствии с теоремой 1 можно утверждать, что линейное отображение не увеличивает размерности отображаемого многообразия: $\dim A(M) \leq \dim M$. ♦

=> Линейное отображение отображает произвольную прямую пространства $V$ в прямую или точку пространства $W$.

Теорема 3. Пусть $\{X_1, \dots, X_n\}$ — произвольный базис $V$, а $Y_1, \dots, Y_n$ — произвольные векторы из $W$. Существует единственное линейное отображение $A: V \longrightarrow W$ такое, что $A(X_1) = Y_1, \dots, A(X_n) = Y_n$.

Note

Иными словами: любое линейное отображение пространства V в другое пространство однозначно определяется его заданием на базисных векторах пространства V.

Доказательство: Поскольку векторы $X_1, \dots, X_n$ — базисные, то существует и единственно разложение любого $X \in V$: $X = x_1 X_1 + \dots + x_n X_n$. Зададим отображение $A: V \longrightarrow W$ формулой

$$A(X) = x_1 Y_1 \oplus \dots \oplus x_n Y_n.$$

Легко проверить свойство его линейности. Кроме того:

$$A(X_j) = A(0 \cdot X_1 + \dots + 1 \cdot X_j + \dots + 0 \cdot X_n) = 0 \cdot Y_1 \oplus \dots \oplus 1 \cdot Y_j \oplus \dots + 0 \cdot Y_n = Y_j,$$

т.е. оно удовлетворяет условиям теоремы.

Предположим теперь, что существует еще одно отображение $B(X)$, удовлетворяющее этим условиям: $B(X_j) = Y_j$. Тогда

$$A(X) = x_1 Y_1 \oplus \dots \oplus x_n Y_n = x_1 B(X_1) \oplus \dots \oplus x_n B(X_n) = B(X),$$

и, на основании определения, $A(X) = B(X)$. ♦

Отображение $S: V \longrightarrow W$ называется суммой линейных отображений $A$ и $B$, если

$$S(X) = A(X) \oplus B(X) \quad \forall X \in V.$$

Отображение $F: V \longrightarrow W$ называется произведением линейного отображения $A$ на число (скаляр) $\lambda \in \mathbb{R}$, если

$$F(X) = \lambda \cdot A(X) \quad \forall X \in V.$$

Ядро и образ линейного отображения

Для линейного отображения $A$ его ядром называется множество векторов из $V$, отображающихся в $O' \in W$:
$$\text{Ker}(A) = \{ X \in V \mid A(X) = O' \}.$$
А его образом называется множество всех векторов из $W$, для каждого из которых существует прообраз из $V$:
$$\text{Im}(A) = \{ Y \in W \mid \exists X \in V, A(X) = Y \}.$$

Теорема 1. $\text{Ker}(A)$ и $\text{Im}(A)$ являются линейными подпространствами соответствующих пространств.

Для линейного отображения $A$ его дефектом называется размерность ядра, а его рангом — размерность образа:
$$\text{dfc}(A) = \dim(\text{Ker}(A)), \quad \text{rank}(A) = \dim(\text{Im}(A)).$$
Отображение называется невырожденным, если
$$\text{dfc}(A) = 0.$$

Теорема 2. Линейное отображение $A$ невырождено тогда и только тогда, когда у каждого образа существует единственный прообраз.

Доказательство.
- Необходимость: Если $A$ невырождено, то $\text{Ker}(A) = \{ O \}$, т.е. единственным вектором из $V$, отображающимся в $O' \in W$, должен быть $O$. Если бы существовали два различных вектора $X_1$ и $X_2$, такие что $A(X_1) = A(X_2)$, то их разность должна быть в ядре, что противоречит предположению.
- Достаточность: Если прообраз для каждого $Y \in W$ единственен, то ядро не может содержать ненулевых векторов, иначе существует вектор $X \neq O$, для которого $A(X) = O'$, что противоречит условию.

Теорема 3. Если $\{ X_1, \dots, X_n \}$ — произвольный базис $V$, то
$$\text{Im}(A) = L(A(X_1), \dots, A(X_n)).$$

Пример. Найти ядро и образ отображения $A: \mathbb{R}^3 \to \mathbb{R}^4$, заданного формулой:
$$A \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} = \begin{pmatrix} x_3 \\ 0 \\ x_1 + x_2 + x_3 \\ x_1 + x_2 - x_3 \end{pmatrix}.$$

Решение. Для определения $\text{Ker}(A)$ найдем фундаментальную систему решений системы уравнений:
$$\begin{aligned} x_3 &= 0, \\ 0 &= 0, \\ x_1 + x_2 + x_3 &= 0, \\ x_1 + x_2 - x_3 &= 0. \end{aligned}$$
Решая систему, получаем:
$$X_1 = \begin{pmatrix} -1 \\ 1 \\ 0 \end{pmatrix}.$$
Таким образом, $\text{Ker}(A) = L(X_1)$, и дефект $A$ равен 1:
$$\text{dfc}(A) = 1.$$

Теперь для нахождения $\text{Im}(A)$ воспользуемся теоремой 3. Базис следует искать среди векторов:
$$Y_1 = A\left( \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} \right) = \begin{pmatrix} 0 \\ 0 \\ 1 \\ 1 \end{pmatrix}, \quad Y_2 = A\left( \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} \right) = \begin{pmatrix} 0 \\ 0 \\ 1 \\ 1 \end{pmatrix},$$
$$Y_3 = A\left( \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \right) = \begin{pmatrix} 1 \\ 0 \\ 1 \\ -1 \end{pmatrix}.$$
Итак, $\text{Im}(A) = L(Y_1, Y_3)$, и ранг $A$ равен 2:
$$\text{rank}(A) = 2.$$

Матрица линейного отображения

Рассмотрим линейное отображение $A: V \to W$, и пусть $\{X_1, \dots, X_n\}$ — базис $V$, а $\{Y_1, \dots, Y_m\}$ — базис $W$. Найдем координаты векторов $A(X_1), \dots, A(X_n)$ в базисе $\{Y_1, \dots, Y_m\}$:

$$\begin{aligned} A(X_1) &= \alpha_{11}Y_1 + \alpha_{21}Y_2 + \dots + \alpha_{m1}Y_m, \\ A(X_2) &= \alpha_{12}Y_1 + \alpha_{22}Y_2 + \dots + \alpha_{m2}Y_m, \\ &\vdots \\ A(X_n) &= \alpha_{1n}Y_1 + \alpha_{2n}Y_2 + \dots + \alpha_{mn}Y_m. \end{aligned}$$

Матрица $A$ с размерами $m \times n$, по столбцам которой стоят координаты образов базисных векторов, называется матрицей линейного отображения $A$ в выбранных базисах:

$$A = \begin{pmatrix} \alpha_{11} & \alpha_{12} & \dots & \alpha_{1n} \\ \alpha_{21} & \alpha_{22} & \dots & \alpha_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ \alpha_{m1} & \alpha_{m2} & \dots & \alpha_{mn} \end{pmatrix}.$$

Почему запись координат в матрицу производится по столбцам? Казалось бы, естественней ставить их по строкам. Объяснение этому решению будет дано ниже.

Теорема. Координаты произвольного вектора

Пусть $X = x_1 X_1 + \dots + x_n X_n$ и его образ $A(X) = y_1 Y_1 + \dots + y_m Y_m$ связаны формулой:

$$\begin{pmatrix} y_1 \\ \vdots \\ y_m \end{pmatrix} = A \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix}.$$

Вот именно для этой последней формулы необходимо было «транспонировать» запись матрицы линейного отображения в начале настоящего пункта.

Доказательство. С помощью приведенных выше формул для $A(X_1), \dots, A(X_n)$ получаем:

$$A(X) = A(x_1 X_1 + \dots + x_n X_n) = x_1 A(X_1) + \dots + x_n A(X_n) = x_1 (\alpha_{11} Y_1 + \dots + \alpha_{m1} Y_m) + \dots + x_n (\alpha_{1n} Y_1 + \dots + \alpha_{mn} Y_m)$$

$$= \begin{pmatrix} x_1 \alpha_{11} + \dots + x_n \alpha_{1n} \\ \vdots \\ x_1 \alpha_{m1} + \dots + x_n \alpha_{mn} \end{pmatrix} = y_1 Y_1 + \dots + y_m Y_m,$$

откуда и следует утверждение теоремы. $\square$

Пример. Найти матрицу линейного отображения

Для отображения:

$$A \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} = \begin{pmatrix} x_3 \\ 0 \\ x_1 + x_2 + x_3 \\ x_1 + x_2 - x_3 \end{pmatrix}$$

в стандартных базисах пространств $\mathbb{R}^3$ и $\mathbb{R}^4$:

• $e_1 = \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}$,
• $e_2 = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}$,
• $e_3 = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}$,

и для $\mathbb{R}^4$:

• $E_1 = \begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \end{pmatrix}$,
• $E_2 = \begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \end{pmatrix}$,
• $E_3 = \begin{pmatrix} 0 \\ 0 \\ 1 \\ 0 \end{pmatrix}$,
• $E_4 = \begin{pmatrix} 0 \\ 0 \\ 0 \\ 1 \end{pmatrix}$.

Решение:

$$A(e_1) = \begin{pmatrix} 0 \\ 0 \\ 1 \\ 1 \end{pmatrix} = 0 \cdot E_1 + 0 \cdot E_2 + 1 \cdot E_3 + 1 \cdot E_4,$$
$$A(e_2) = \begin{pmatrix} 0 \\ 0 \\ 1 \\ 1 \end{pmatrix} = 0 \cdot E_1 + 0 \cdot E_2 + 1 \cdot E_3 + 1 \cdot E_4,$$
$$A(e_3) = \begin{pmatrix} 1 \\ 0 \\ 1 \\ -1 \end{pmatrix} = 1 \cdot E_1 + 0 \cdot E_2 + 1 \cdot E_3 - 1 \cdot E_4.$$

Матрица отображения $A$ в выбранных базисах:

$$A = \begin{pmatrix} 0 & 0 & 1 \\ 0 & 0 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & -1 \end{pmatrix}.$$

Она совпадает с матрицей коэффициентов при переменных $x_1, x_2, x_3$ в выражениях координат вектора $A(X)$. $\square$

Линейный оператор

Линейное отображение линейного (векторного) пространства $V$ в себя $A : V \to V$ называется линейным преобразованием $V$ или линейным оператором на $V$.

В дальнейшем под выражением оператор понимается исключительно линейный оператор (и линейное пространство $V$ предполагается конечномерным!).

Свойства линейности:

1. Аддитивность:
   $$A(X_1 + X_2) = A(X_1) + A(X_2)$$

2. Однородность (гомогенность):
   $$A(\alpha_1 X_1) = \alpha_1 A(X_1)$$

Или, в эквивалентном виде:

$$A(\alpha_1 X_1 + \alpha_2 X_2) = \alpha_1 A(X_1) + \alpha_2 A(X_2)$$

где $\forall \, X_1, X_2 \in V$, $\forall \, \alpha_1, \alpha_2 \in \mathbb{R}$ или $\mathbb{C}$ (в зависимости от того, вещественное ли пространство $V$, или комплексное).

Примеры линейных операторов

Пример 1. В пространстве $\mathbb{R}^3$ рассмотрим следующие действия над вектором $(x, y, z)$:

1. Поворот вокруг прямой $x = y = 2z$ на угол $\frac{\pi}{3}$;
2. Зеркальное отражение относительно плоскости $3x - y + z = 0$;
3. Растяжение в $3.14$ раза.

Все это — примеры линейных операторов. Однако отображение сдвига:

$$(x, y, z) \mapsto (x + 1, y, z + 2)$$

не является линейным оператором, поскольку:

$$\alpha(x, y, z) = (\alpha x, \alpha y, \alpha z) \mapsto (\alpha x + 1, \alpha y, \alpha z + 2) \neq \alpha(x + 1, y, z + 2)$$

Пример 2. Задачу интерполяции можно интерпретировать как построение некоторого отображения. В интерполяционной таблице

$$\begin{array}{|c|c|c|c|} \hline x_1 & x_2 & \cdots & x_n \\ \hline y_1 & y_2 & \cdots & y_n \\ \hline \end{array}$$

будем считать узлы $\{ x_j \}^n_{j=1}$ фиксированными, а значения $\{ y_j \}^n_{j=1}$ — переменными. Эта таблица однозначно определяет интерполяционный полином:

$$f(x) = A_0 + A_1 x + \cdots + A_{n-1} x^{n-1}$$

со свойством $f(x_j) = y_j$ при $j \in \{ 1, \dots, n \}$. При этом $\{ A_j \}^n_{j=0} \subset \mathbb{C}$. Будет ли получившееся отображение

$$(y_1, \dots, y_n) \mapsto (A_0, A_1, \dots, A_{n-1})$$

оператором на $\mathbb{C}^n$? Покажем, что отображение

$$A(y_1, \dots, y_n) = f(x) \in \mathbb{C}[x]$$

является линейным отображением. Действительно, решением задачи интерполяции для таблицы

$$\begin{array}{|c|c|c|c|} \hline x_1 & x_2 & \cdots & x_n \\ \hline \alpha y_1 & \alpha y_2 & \cdots & \alpha y_n \\ \hline \end{array}$$

при $\alpha \in \mathbb{C}$ является полином $\alpha f(x)$. Если же, вдобавок, решением задачи интерполяции для таблицы

$$\begin{array}{|c|c|c|c|} \hline x_1 & x_2 & \cdots & x_n \\ \hline z_1 & z_2 & \cdots & z_n \\ \hline \end{array}$$

является полином $g(x) \in \mathbb{C}[x]$, $\deg g(x) \leq n-1$, то решением задачи интерполяции для таблицы

$$\begin{array}{|c|c|c|c|} \hline x_1 & x_2 & \cdots & x_n \\ \hline y_1 + z_1 & y_2 + z_2 & \cdots & y_n + z_n \\ \hline \end{array}$$

будет полином $f(x) + g(x)$, и этот полином будет единственным решением среди полиномов степеней $\leq n-1$. Таким образом, линейность отображения $A$ установлена.

Далее, множество $P_{n-1}$ полиномов из $\mathbb{C}[x]$ степеней $\leq n-1$ изоморфно пространству $\mathbb{C}^n$. Следовательно, «сложное» отображение

$$(y_1, \dots, y_n) \mapsto f(x) = A_0 + A_1 x + \cdots + A_{n-1} x^{n-1} \mapsto (A_0, A_1, \dots, A_{n-1})$$

является линейным отображением из $\mathbb{C}^n$ в $\mathbb{C}^n$, т.е. оператором на $\mathbb{C}^n$.

Матрица оператора

Рассмотрим оператор A на V и пусть $\{X_1, \dots, X_n\}$ — базис V. Являясь частным случаем линейного отображения, оператор должен обладать и соответствующей матрицей. Существенной особенностью, отличающей наш случай от рассмотренного в пункте ☞ МАТРИЦА ЛИНЕЙНОГО ОТОБРАЖЕНИЯ, является невозможность произвола при выборе базиса для Im(A). Поскольку Im(A) является подпространством V, то было бы слишком большой роскошью иметь два разных базиса для одного и того же пространства.

Найдем координаты образов базисных векторов $A(X_1), \dots, A(X_n)$ в том же базисе $\{X_1, \dots, X_n\}$:

$$\begin{aligned} A(X_1) &= \alpha_{11}X_1 + \alpha_{21}X_2 + \dots + \alpha_{n1}X_n, \\ A(X_2) &= \alpha_{12}X_1 + \alpha_{22}X_2 + \dots + \alpha_{n2}X_n, \\ &\dots \\ A(X_n) &= \alpha_{1n}X_1 + \alpha_{2n}X_2 + \dots + \alpha_{nn}X_n. \end{aligned}$$

Матрица A =
$$\begin{pmatrix} \alpha_{11} & \alpha_{12} & \dots & \alpha_{1n} \\ \alpha_{21} & \alpha_{22} & \dots & \alpha_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ \alpha_{n1} & \alpha_{n2} & \dots & \alpha_{nn} \end{pmatrix}$$

в столбцах которой стоят координаты образов базисных векторов, называется матрицей оператора A в базисе $\{X_1, \dots, X_n\}$.

Пример.

Известны образы базисных векторов R³ под действием оператора A:

$$A\begin{pmatrix} 5 \\ 3 \\ 1 \end{pmatrix} = \begin{pmatrix} -2 \\ 1 \\ 0 \end{pmatrix}, \quad A\begin{pmatrix} 1 \\ -3 \\ -2 \end{pmatrix} = \begin{pmatrix} -1 \\ 3 \\ 0 \end{pmatrix}, \quad A\begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} = \begin{pmatrix} -2 \\ -3 \\ 0 \end{pmatrix}.$$

Найти матрицу этого оператора в исходном базисе.

Решение. Элементы матрицы A ищутся по формулам из определения, которые можно переписать в матричном виде:
$$[X_1, \dots, X_n]A = [A(X_1), \dots, A(X_n)]$$
Откуда:
$$A = [X_1, \dots, X_n]^{-1}[A(X_1), \dots, A(X_n)].$$

И для нашего примера эта формула дает:

$$A = \begin{pmatrix} 5 & 1 & 1 \\ 3 & -3 & 2 \\ 1 & -2 & 1 \end{pmatrix}^{-1} \begin{pmatrix} -2 & -1 & -2 \\ 1 & 3 & -3 \\ 0 & 0 & 0 \end{pmatrix} = \begin{pmatrix} 1 & -3 & 5 \\ -1 & 4 & -7 \\ -3 & 11 & -18 \end{pmatrix} \begin{pmatrix} -2 & -1 & -2 \\ 1 & 3 & -3 \\ 0 & 0 & 0 \end{pmatrix} = \begin{pmatrix} -5 & -10 & 7 \\ 6 & 13 & -10 \\ 17 & 36 & -27 \end{pmatrix}.$$

Теорема.

Если C — матрица перехода от старого базиса к новому, то матрицы A и B оператора в старом и новом базисах связаны формулой:

$$B = C^{-1} A C.$$

Доказательство. Пусть $\{X_1, \dots, X_n\}$ — старый базис, $\{Y_1, \dots, Y_n\}$ — новый базис, и разложения вектора X и его образа Y в этих базисах имеют вид:

$$X = x_1X_1 + \dots + x_nX_n, \quad Y = A(X) = y_1X_1 + \dots + y_nX_n.$$

На основании результатов ☞ ПУНКТА, имеем:

$$\begin{pmatrix} x_1 \\ \vdots \\ x_n \end{pmatrix} = C \begin{pmatrix} y_1 \\ \vdots \\ y_n \end{pmatrix}.$$

Получаем цепочку равенств:

$$B \begin{pmatrix} x_1 \\ \vdots \\ x_n \end{pmatrix} = \begin{pmatrix} y_1 \\ \vdots \\ y_n \end{pmatrix} = C^{-1} \begin{pmatrix} y_1 \\ \vdots \\ y_n \end{pmatrix} = C^{-1} A \begin{pmatrix} x_1 \\ \vdots \\ x_n \end{pmatrix} = C^{-1} A C \begin{pmatrix} x_1 \\ \vdots \\ x_n \end{pmatrix}.$$

Равенство имеет место для любого столбца, и, в частности, для столбцов:

$$\begin{pmatrix} 1 \\ 0 \\ \vdots \\ 0 \end{pmatrix}, \quad \begin{pmatrix} 0 \\ 1 \\ \vdots \\ 0 \end{pmatrix}, \dots, \quad \begin{pmatrix} 0 \\ 0 \\ \vdots \\ 1 \end{pmatrix}.$$

Объединяя эти n равенств в одно матричное, получим:

$$B \cdot E = C^{-1} \cdot A \cdot C \cdot E,$$
откуда и следует доказываемое.

!! note Теорема
Оператор обратим тогда и только тогда, когда его определитель отличен от нуля.

Теорема

Линейное пространство Hom(V, V) операторов на V, $\text{dim} V = n$, изоморфно линейному пространству квадратных матриц порядка n (с элементами из R или из C).

Теорема

В любом базисе пространства:

а) матрица нулевого оператора O является нулевой матрицей O, а матрица тождественного оператора E является единичной матрицей E; обратно: если матрица оператора в этом базисе — нулевая (единичная), то оператор является нулевым (соответственно, тождественным);

б) матрица произведения операторов совпадает с произведением матриц этих операторов;

в) коммутирующим операторам соответствуют коммутирующие матрицы;

Оператор в евклидовом пространстве

Каков "физический" смысл определителя оператора?

Пусть на плоскости $\mathbb{R}^2$ задано стандартное скалярное произведение. Рассмотрим оператор, отображающий векторы по правилу

$$\begin{pmatrix} y_1 \\ y_2 \end{pmatrix} = \begin{pmatrix} 1 & -3 \\ 1 & -1 \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix}$$

Свойство линейности оператора как отображения плоскости проявляется в том, что параллельные отрезки он отображает в параллельные же отрезки и, следовательно, любой параллелограмм отображается им в параллелограмм.

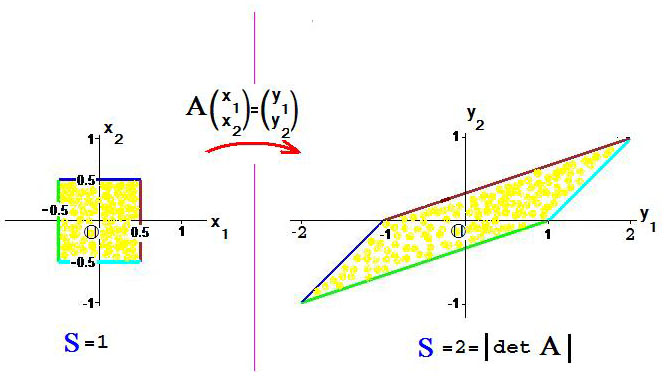
Площади соответствующих параллелограммов оказываются связанными через определитель матрицы — более точно, через модуль этого определителя. Причем этот результат не зависит от расположения отображаемой фигуры: коэффициент растяжения будет одинаков в любом месте плоскости.

В рассмотренном примере это проверяется непосредственно; что касается обобщения на произвольное евклидово пространство, в котором понятие объема вводится аксиоматически то справедлив следующий результат.

Оператор свертки

Свертка (англ. convolution) — операция над парой матриц A (размера $n_x \times n_y$) и B (размера $m_x \times m_y$), результатом которой является матрица C = A * B размера $(n_x - m_x + 1) \times (n_y - m_y + 1)$. Каждый элемент результата вычисляется как скалярное произведение матрицы B и некоторой подматрицы A такого же размера (подматрица определяется положением элемента в результате). То есть,

$$C_{i,j} = \sum_{u=0}^{m_x-1} \sum_{v=0}^{m_y-1} A_{i+u, j+v} B_{u,v}.$$

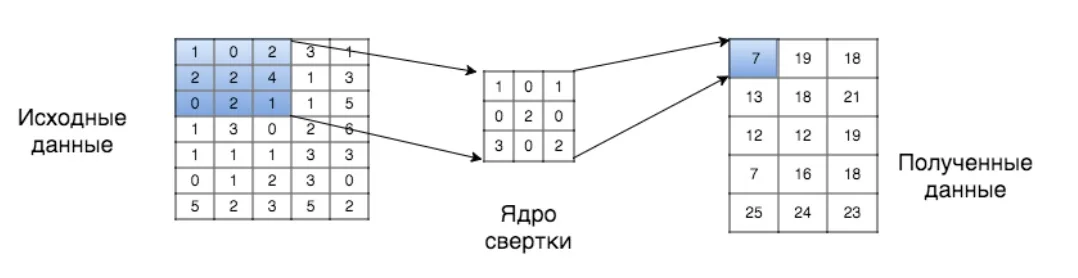
На Рисунке можно видеть, как матрица B «двигается» по матрице A, и в каждом положении считается скалярное произведение матрицы B и той части матрицы A, на которую она сейчас наложена. Получившееся число записывается в соответствующий элемент результата.

Логический смысл свертки такой — чем больше величина элемента свертки, тем больше эта часть матрицы A была похожа на матрицу B (похожа в смысле скалярного произведения). Поэтому матрицу A называют изображением, а матрицу B — фильтром или ядром.

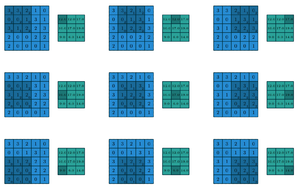
Анимация:

Матрица B:

$$B = \begin{pmatrix} 1 & 0 & 1 \\ 1 & 0 & 1 \\ 1 & 0 & 1 \end{pmatrix}$$

Процесс свертки:

1. Начинаем с того, что матрица B "накладывается" на верхний левый угол матрицы A.
2. Складываем произведения элементов из B и соответствующих элементов из A. Получаем число, которое записываем в элемент результата.
3. Затем B "сдвигается" по матрице A, и процесс повторяется для каждой позиции.

Зачем оно нам надо?

Математическое обоснование оператора Прюитта

Оператор Прюитта представляет собой дискретное приближение производных изображения, полученное методом конечных разностей. Его математическое обоснование можно описать следующим образом:

1. Фундамент идеи

Пусть функция $f(x,y)$ описывает яркость изображения. Тогда её частные производные по $x$ и $y$ можно аппроксимировать центральными конечными разностями:
$$f_x(x,y) \approx \frac{f(x+1,y) - f(x-1,y)}{2}, \quad f_y(x,y) \approx \frac{f(x,y+1) - f(x,y-1)}{2}.$$
Однако, вместо простого вычитания, для повышения устойчивости к шуму и учета соседних пикселей используется свёрточная маска.

2. Вывод масок оператора

Для приближения производной по $x$ оператор Прюитта использует ядро:
$$G_x = \begin{bmatrix} -1 & 0 & +1 \\ -1 & 0 & +1 \\ -1 & 0 & +1 \end{bmatrix},$$
а для производной по $y$ – ядро:
$$G_y = \begin{bmatrix} -1 & -1 & -1 \\ 0 & 0 & 0 \\ +1 & +1 & +1 \end{bmatrix}.$$
Каждое из этих ядер можно интерпретировать как операцию свёртки с изображением, где суммирование по строкам или столбцам выполняет усреднение, а разность между «правой» и «левой» (или «нижней» и «верхней») группами пикселей – приближает производную.

3. Математическая интерпретация

Если рассматривать свёртку ядра $G_x$ с изображением, то для центрального пикселя получается:
$$(G_x * f)(x,y) = \bigl[f(x+1,y-1) + f(x+1,y) + f(x+1,y+1)\bigr] - \bigl[f(x-1,y-1) + f(x-1,y) + f(x-1,y+1)\bigr].$$
Это соответствует сумме разностей яркостей справа и слева, что является приближением $f_x(x,y)$. Аналогично для $G_y$ свёртка дает приближение $f_y(x,y)$.

4. Оценка градиента

После вычисления приближённых значений производных по $x$ и $y$ часто вычисляют величину градиента:
$$\left|\nabla f(x,y)\right| = \sqrt{(G_x * f)^2 + (G_y * f)^2},$$
а направление градиента определяется как
$$\theta(x,y) = \arctan\frac{(G_y * f)}{(G_x * f)}.$$

Таким образом, математическое доказательство корректности оператора Прюитта базируется на идее аппроксимации непрерывных производных методом центральных конечных разностей с усреднением по окрестности пикселя, что реализовано через свёрточные ядра.

Некоторые другие полезные опраторы на основе Свертки

1. Фильтр Гаусса (Gaussian Filter):
   Этот фильтр используется для сглаживания изображений, уменьшения шума и устранения мелких деталей. Он работает путем применения Гауссовой функции к изображению.

Формула фильтра Гаусса:
$$G(x, y) = \frac{1}{2\pi\sigma^2} \exp\left(-\frac{x^2 + y^2}{2\sigma^2}\right)$$
Где:
- σ — стандартное отклонение,
- x, y — координаты пикселя.

Этот фильтр помогает в задачах, таких как детектирование контуров и распознавание объектов.

1. Фильтр Собеля (Sobel Filter):
   Фильтр Собеля используется для нахождения градиента изображения, что помогает в выделении границ объектов. Оператор включает два фильтра: один для выделения горизонтальных границ, а другой — для вертикальных.

Горизонтальный фильтр:
$$S_x = \begin{bmatrix} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \end{bmatrix}$$

Вертикальный фильтр:
$$S_y = \begin{bmatrix} -1 & -2 & -1 \\ 0 & 0 & 0 \\ 1 & 2 & 1 \end{bmatrix}$$

Суммарный градиент вычисляется как:
$$G = \sqrt{S_x^2 + S_y^2}$$

1. Фильтр Робертса (Roberts Cross Filter):
   Фильтр Робертса используется для детектирования краев, особенно в случае малых изменений интенсивности на изображении. Этот оператор работает с малыми матрицами и вычисляет градиент изображения в диагонах.

Горизонтальный фильтр:
$$R_x = \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}$$

Вертикальный фильтр:
$$R_y = \begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix}$$

1. Фильтр Шарра (Scharr Filter):
   Этот фильтр является модификацией фильтра Собеля и используется для более точного вычисления градиента изображения, особенно для выделения горизонтальных и вертикальных границ.

Горизонтальный фильтр:
$$S_x = \begin{bmatrix} -3 & 0 & 3 \\ -10 & 0 & 10 \\ -3 & 0 & 3 \end{bmatrix}$$

Вертикальный фильтр:
$$S_y = \begin{bmatrix} -3 & -10 & -3 \\ 0 & 0 & 0 \\ 3 & 10 & 3 \end{bmatrix}$$

Фильтр Шарра более чувствителен к изменениям и дает лучшие результаты для контуров.

Операторы Эрозии и Дилатации

Морфологические операторы:
Эти операторы используются для обработки изображений, которые содержат бинарные данные, например, при обработке контуров объектов.

• Эрозия (Erosion): уменьшает размер объекта в изображении, вытесняя пиксели объекта за пределы.
• Дилатация (Dilation): увеличивает размер объекта, расширяя его границы.

Благодарности и список использованных источников

1. Многие материалы были заимстованы у Утешева Алексея Юрьевича из (Интерактивной информационно-консультационной среды)[https://cx53922.tmweb.ru/vf5/mapping]