Лекция 3 Изоморфизм линейных пространств. Метрические, нормированные, Евклидовы пространства. Собственные вектора.

Презентация доступна здесь

Как мы знаем линейных пространств можно придумать довольно много, причем некоторые эти линейные пространства каким-то образом взаимосвязаны с другими.
Так, на практике мы заметили, что система уравнений соотвествует некоторой матрице. Попробуем обобщить наши наблюдения в некоторой математической форме.

Изоморфизм линейных пространств

Пусть имеются два линейных пространства разной природы:
V с операцией + и W с операцией ⊞. Может оказаться так, что эти пространства «очень похожи», и свойства одного получаются простым «переводом» свойств другого.

Говорят, что пространства V и W изоморфны, если между множествами их элементов можно установить такое взаимно-однозначное соответствие, что если X ↔ X′ и Y ↔ Y′, то X + Y ↔ X′ ⊞ Y′ и λX ↔ λX′.

=>
При изоморфизме пространств V и W нулевому вектору одного пространства будет соответствовать нулевой вектор другого пространства.

Пример 1

Пространство **Rⁿ** изоморфно пространству **Pⁿ⁻¹**. В самом деле, изоморфизм устанавливается соответствием: [a₁, …, aₙ] ↔ a₁ + a₂x + ⋯ + aₙxⁿ⁻¹

Пример 2

Пространство **Rᵐˣⁿ** вещественных матриц порядка **m × n** изоморфно пространству **Rᵐⁿ**. Изоморфизм устанавливается с помощью операции векторизации матрицы (матрица «вытягивается» в один столбец).

Примечание: Понятие изоморфизма вводится для того, чтобы исследование объектов, возникающих в различных областях алгебры, но с «похожими» свойствами операций, вести на примере одного образца, отрабатывая на нем результаты, которые можно будет потом дешево тиражировать.

Теорема

Формулировка

Любое векторное пространство **V** размерности **d** изоморфно **Rᵈ**.

Доказательство

Изоморфизм можно установить следующим соответствием. Если {X₁, …, Xᵈ} — какой-то базис V, то вектору X ∈ V поставим в соответствие набор его координат в этом базисе:
X = x₁X₁ + ⋯ + xᵈXᵈ⇒ X ↦ [x₁, …, xᵈ] ∈ Rᵈ.

Исхожя из того факта, что Если dimV=d>0, то любая система из d линейно независимых векторов пространства образует базис этого пространства такое соответствие будет взаимно-однозначным, а проверка двух свойств изоморфизма тривиальна.

Примечание: Последний результат позволяет свести исследование свойств произвольного линейного пространства V к исследованию свойств пространства Rᵈ. Лишь бы только удалось нам найти базис пространства V, а также разложение произвольного вектора по этому базису. Однако некоторые теоретические заключения можно сделать, основываясь только лишь на фактах принципиального существования базиса и возможности разложения по нему произвольного вектора.

Метрическое пространство

Рассмотрим произвольное множество X. Функция ρ : X × X → [0, +∞) называется метрикой, если выполнены следующие три условия:

1. ρ(x, y) = 0 тогда и только тогда, когда x = y;
2. ρ(x, y) = ρ(y, x) для ∀ x, y ∈ X;
3. ρ(x, y) ≤ ρ(x, z) + ρ(z, y) для ∀ x, y, z ∈ X. Свойство 3 называется неравенством треугольника.

Пара (X, ρ) называется метрическим пространством.

Метрика — это расстояние между элементами. Из определения следует, что метрическое пространство представляет собой произвольное множество с введённой на всевозможных упорядоченных парах элементов этого множества функцией, значение которой на данной паре считается расстоянием между элементами этой пары. Никакого дополнительного уточнения свойств множества X не требуется.

Приведём примеры метрических пространств.

Пример 1.
Рассмотрим любое множество X. Если ввести на множестве пар элементов множества X функцию ρ, для которой:

• ρ(x, y) = 1 при x ≠ y,
• ρ(x, x) = 0 при всех x, y ∈ X,

то для неё выполнены все свойства метрики, поэтому (X, ρ) является метрическим пространством. Оно называется дискретным метрическим пространством, а сама метрика ρ называется дискретной.

В частности, в качестве множества X можно взять множество всех натуральных чисел N. В таком случае, если два числа не равны, то значение ρ на них равно 1, а в противном случае — нулю.

Пример 2.
Рассмотрим множество R² всех пар действительных чисел. Как известно, R² является векторным пространством, поэтому его элементы будем обозначать жирным шрифтом. Если x = (x₁, x₂), а y = (y₁, y₂), где xᵢ, yᵢ ∈ R, i = 1, 2, то можно ввести метрику:

ρ₁(x, y) = |x₁ − y₁| + |x₂ − y₂|.

Напомним, что на лекциях по линейной алгебре мы ввели норму на пространстве R², которая задавалась равенством:

∥x∥₁ = |x₁| + |x₂|.

Легко видеть, что:

ρ₁(x, y) = ∥x − y∥₁.

Все свойства метрики легко проверяются. Свойство 3, например, следует из неравенства треугольника для норм, которое доказывалось на линейной алгебре:

ρ₁(x, y) = ∥x − y∥₁ = ∥x − z + z − y∥₁ ≤ ∥x − z∥₁ + ∥z − y∥₁ = ρ₁(x, z) + ρ₁(z, y).

Пример 3.

Можно, однако, ввести на R² метрику с помощью формулы, которая в аналитической геометрии задаёт расстояние между двумя точками с координатами (x₁, x₂) и (y₁, y₂), а именно:

ρ₂(x, y) = √((x₁ − y₁)² + (x₂ − y₂)²).

Эта метрика получается из евклидовой нормы ∥x∥₂ = √(x₁² + x₂²), которую мы ввели на линейной алгебре. То, что функция ρ₂ действительно является метрикой, проверяется, как и для ρ₁ в предыдущем пункте.

Примечание: Таким образом, мы видим, что на одном и том же множестве можно задавать разные метрики.

Понятие нормы

В примерах 2 и 3 мы использовали понятие векторного пространства, поэтому необходимо вспомнить это определение из курса линейной алгебры. Таким образом, множество X из определения метрического пространства рассматривалось с некоторыми ограничениями, так как мы указали, что это не просто произвольное множество, а векторное пространство.

На всякий случай напомним определение нормы, которое давалось в курсе линейной алгебры.

Пусть V — линейное пространство. Функция | · | : V → [0, +∞) называется нормой, если выполнены следующие условия:

1) | v | = 0 если и только если v = 0, то есть вектор v является нейтральным элементом векторного пространства V.
2) Для любого вещественного (или комплексного) числа λ и любого вектора v ∈ V выполнено равенство | λ v | = |λ| | v |.
3) Для любых x, y ∈ V выполнено неравенство треугольника: | x + y | ≤ | x | + | y |.

Линейное пространство V с введённой на нём нормой обозначается (V, |·|) и называется нормированным пространством.

Любое нормированное пространство можно сделать метрическим с метрикой ρ, задаваемой равенством:

ρ(x, y) = ∥x − y∥

Норма вводится только на векторных пространствах, поэтому класс нормированных пространств содержится в классе метрических.

Нормированное пространство

Пусть в линейном пространстве V определена функция, которая ставит в соответствие каждому вектору X ⊂ V вещественное число, называемое нормой вектора и обозначаемое ∥X∥; при этом функция подчиняется аксиомам:

1. если ∥X∥ = 0, то X = O;
2. ∥X + Y∥ ≤ ∥X∥ + ∥Y∥ для ∀ {X, Y} ⊂ V (неравенство треугольника);
3. ∥αX∥ = |α| ⋅ ∥X∥ для ∀ X ∈ V и ∀ α ∈ R, если пространство вещественно, и ∀ α ∈ C, если оно комплексно (однородность нормы).

Пространство V с введенной в нем нормой называется нормированным (линейным) пространством.

Из этих аксиом вытекает следующее свойство нормы, которое часто включают в состав аксиом.

Теорема

        Любая норма должна быть неотрицательной функцией: ∥X∥ ≥ 0 для ∀ X ∈ V.

Док-во:
Действительно, из аксиомы 3 вытекает, что норма нулевого вектора должна быть равна 0:

∥O∥ = ∥0 ⋅ O∥ = 0 ∥O∥ = 0.

Из аксиом 2 и 3 тогда следует:
0 = ∥O∥ = ∥X - X∥ ≤ ∥X∥ + ∥-X∥ = 2∥X∥ => ∥X∥ ≥ 0 для ∀ X ∈ V.

В широком классе вещественных пространств норма может быть введена естественным образом.

Примечание: При этом любое нормированное пространство является метрическим, потому что можно взять вектор, соединяющий две точки, посмотреть на его длину и называть её расстоянием.

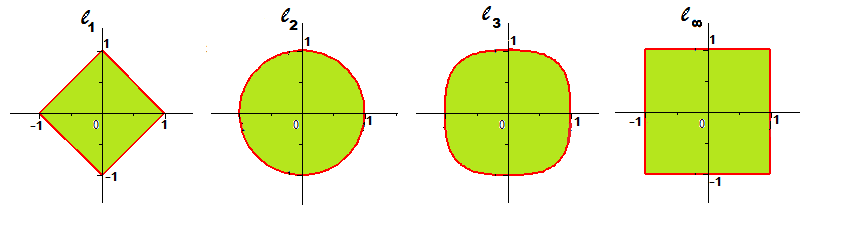
Различные способы задания нормы в одном и том же линейном пространстве порождают различные формы окрестности вектора (точки) этого пространства. Для примера изобразим 1-окрестность начала координат в R² (``единичный круг''):

Норма матрицы

Любую матрицу A порядка m × n с вещественными или комплексными элементами можно векторизовать, т.е. считать её вектором из Rᵐⁿ или из Cᵐⁿ. Любая норма, введённая в этих пространствах, породит и норму в линейном пространстве матриц.

Для матрицы A ∈ Cᵐˣⁿ евклидова норма вводится формулой:

∥A∥ₓ = √∑ₖₖ |aₖₖ|².

С использованием операции вычисления следа матрицы, эту формулу для вещественных матриц можно переписать в виде:

∥A∥ₓ = √Sp(A ⋅ Aᵀ) = √Sp(AᵀA).

Евклидово пространство

Вещественное линейное пространство E называется евклидовым, если в этом пространстве определена функция, ставящая в соответствие паре векторов {X, Y} ⊂ E вещественное число, называемое скалярным произведением векторов X и Y, и обозначаемое ⟨X, Y⟩ или (X, Y). При этом функция подчиняется аксиомам:

1. ⟨X, Y⟩ = ⟨Y, X⟩ для {X, Y} ⊂ E;
2. ⟨X₁ + X₂, Y⟩ = ⟨X₁, Y⟩ + ⟨X₂, Y⟩ для {X₁, X₂, Y} ⊂ E;
3. ⟨λX, Y⟩ = λ⟨X, Y⟩ для {X, Y} ⊂ E, λ ∈ R;
4. ⟨X, X⟩ > 0 для ∀X ≠ O, ⟨O, O⟩ = 0.

Из аксиом 1 и 2 вытекает свойство линейности скалярного произведения и по второму вектору:

2'. ⟨X, Y₁ + Y₂⟩ = ⟨X, Y₁⟩ + ⟨X, Y₂⟩ для {X, Y₁, Y₂} ⊂ E.

Пример
Линейное пространство Rⁿˣⁿ вещественных квадратных матриц порядка n. Скалярное произведение введем формулой:

$$\langle A, B \rangle = \sum_{j,k=1}^{n} a_{jk} b_{jk}.$$

На основании аксиом скалярного произведения, его вычисление для произвольных векторов $X$ и $Y$ может быть сведено к вычислению скалярных произведений векторов произвольного базиса. В самом деле, если система $\{ X_1, \dots, X_n \}$ составляет базис пространства $E$, то, разложив оба вектора по этому базису

$$X = x_1 X_1 + \dots + x_n X_n$$
и
$$Y = y_1 X_1 + \dots + y_n X_n,$$

получаем:

$$\langle X, Y \rangle = \langle x_1 X_1 + \dots + x_n X_n, y_1 X_1 + \dots + y_n X_n \rangle$$

$$= x_1 y_1 \langle X_1, X_1 \rangle + x_1 y_2 \langle X_1, X_2 \rangle + \dots + x_1 y_n \langle X_1, X_n \rangle$$
$$+ x_2 y_1 \langle X_2, X_1 \rangle + x_2 y_2 \langle X_2, X_2 \rangle + \dots + x_2 y_n \langle X_2, X_n \rangle$$
$$+ \dots$$
$$+ x_n y_1 \langle X_n, X_1 \rangle + x_n y_2 \langle X_n, X_2 \rangle + \dots + x_n y_n \langle X_n, X_n \rangle.$$

Таким образом, выражение для скалярного произведения можно записать в матричной форме как:

$$\langle X, Y \rangle = \begin{pmatrix} x_1 & x_2 & \dots & x_n \end{pmatrix} \begin{pmatrix} \langle X_1, X_1 \rangle & \langle X_1, X_2 \rangle & \dots & \langle X_1, X_n \rangle \\ \langle X_2, X_1 \rangle & \langle X_2, X_2 \rangle & \dots & \langle X_2, X_n \rangle \\ \vdots & \vdots & \ddots & \vdots \\ \langle X_n, X_1 \rangle & \langle X_n, X_2 \rangle & \dots & \langle X_n, X_n \rangle \end{pmatrix} \begin{pmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{pmatrix}.$$

Итак, при изменении векторов $X$ и $Y$ в последней формуле изменяются только строка и столбец координат, а промежуточная матрица остаётся неизменной. Задание этой матрицы, следовательно, полностью определяет скалярное произведение в $E$. Фактически, задание скалярного произведения в разобранном выше примере пространства $R^n$ по формуле

$$\langle X, Y \rangle = X^\top A Y$$

можно рассматривать как частный случай этого при подходящем подборе базисных векторов.

Неравенство Коши-Буняковского

Неравенство Коши-Буньяковского является важным математическим результатом в линейной алгебре и теории векторных пространств. Оно выражает связь между скалярным произведением двух векторов и их длинами.

Пусть $X$ и $Y$ — два вектора в евклидово пространство (или пространство с внутренним произведением). Тогда выполняется неравенство Коши-Буньяковского:

$$|\langle X, Y \rangle| \leq |X| \cdot |Y|,$$

где:

• $\langle X, Y \rangle$ — скалярное произведение векторов $X$ и $Y$,
• $|X|$ и $|Y|$ — длины (нормы) векторов $X$ и $Y$, то есть $|X| = \sqrt{\langle X, X \rangle}$ и $|Y| = \sqrt{\langle Y, Y \rangle}$.

Доказательство неравенства Коши-Буньяковского часто выполняется с использованием метода неравенства Дженсона или неравенства для квадратичных форм.

1. Рассмотрим произвольное скалярное произведение:

$$\langle X, Y \rangle = \langle X, Y \rangle - \langle X, X \rangle + \langle X, X \rangle.$$

1. Это выражение можно записать как:

$$\langle X, Y \rangle = \frac{1}{2} \left( \langle X, Y \rangle + \langle Y, X \rangle \right).$$

1. Из этого выражения можно показать, что скалярное произведение между двумя векторами всегда меньше либо равно произведению их длин, что и соответствует неравенству.

Геометрический смысл

Неравенство Коши-Буньяковского можно интерпретировать геометрически: оно утверждает, что абсолютное значение скалярного произведения двух векторов не может превышать произведение их длин. Это означает, что угол между двумя векторами не может быть больше \( 90^\circ \), и наибольшее значение скалярного произведения достигается, когда два вектора коллинеарны, то есть лежат на одной прямой.

Углом между векторами

Определение: Углом между векторами $X$ и $Y$ называется угол

$$\varphi = \angle(X, Y) = \arccos \frac{\langle X, Y \rangle}{|X| \cdot |Y|}$$

В силу неравенства Коши-Буняковского, данное определение непротиворечиво: выражение под знаком арккосинуса всегда находится в диапазоне $[-1, 1]$.

Векторы $X$ и $Y$ называются ортогональными, если угол между ними равен $\frac{\pi}{2}$, что эквивалентно:

$$\langle X, Y \rangle = 0.$$

Данное определение является естественным обобщением понятия угла на плоскости и в трёхмерном пространстве. Хотя человеческий мозг не привык работать с размерностями, превышающими 3, эта абстракция находит практическое применение, например, в задачах информационного поиска и анализа данных.

Ортоганилзация

Пусть $\dim E = n$ и векторы $\{ X_1, \dots, X_n \}$ составляют базис $E$. Этот базис называется ортогональным, если векторы попарно ортогональны: $X_j \perp X_k$ для $j \neq k$.

Базис называется нормированным, если каждый его вектор имеет единичную длину: $|X_j| = 1$.

Базис называется ортонормированным, если он и ортогонален, и нормирован, то есть:

$$\langle X_j, X_k \rangle = \delta_{jk},$$

где $\delta_{jk}$ — символ Кронекера.

Ортогональный базис будем обозначать как $E_1, \dots, E_n$.

Вопрос: Чему равно расстояние между двумя векторами ортонормированного базиса?

В пространстве $\mathbb{R}^n$ стандартным ортогональным базисом является базис, состоящий из векторов:

$$e_j = \left[ 0, \dots, 0, \underbrace{1}_{\text{в } j\text{-м месте}}, 0, \dots, 0 \right]^T, \quad j \in \{1, \dots, n\}.$$

Существование ортогонального базиса в произвольном евклидовом пространстве требует дополнительного доказательства.

Теорема

Если ненулевые векторы $X_1, \dots, X_n$ попарно ортогональны, то они линейно независимы.

Доказательство

Предположим, что векторы линейно зависимы, т.е. существует линейная комбинация:

$$\lambda_1 X_1 + \dots + \lambda_n X_n = O.$$

Пусть домножим это равенство скалярно на $X_1$:

$$\lambda_1 \langle X_1, X_1 \rangle + \dots + \lambda_n \langle X_1, X_n \rangle = 0.$$

Поскольку $\langle X_1, X_j \rangle = 0$ для $j \in \{2, \dots, n\}$, получаем:

$$\lambda_1 \langle X_1, X_1 \rangle = 0.$$

Так как $X_1 \neq O$, то $\langle X_1, X_1 \rangle \neq 0$, следовательно, $\lambda_1 = 0$.

Аналогично можно доказать, что $\lambda_j = 0$ для всех $j$, что противоречит предположению о линейной зависимости.

Таким образом, векторы $X_1, \dots, X_n$ линейно независимы.

Введение в идею Собственных векторов и чисел

Рассмотрим произвольную квадратную матрицу, например:

$$A = \begin{bmatrix} 2 & 6 \\ -1 & -1 \end{bmatrix}$$

И умножим данную матрицу справа на какой-нибудь подходящий столбец.
Мне пришёл в голову вектор:

$$b = \begin{bmatrix} -1 \\ -5 \end{bmatrix}$$

Вроде ничего примечательного — умножили матрицу $A$ на вектор-столбец $b$ и получили другой вектор-столбец:

$$c = \begin{bmatrix} 1 \\ 4 \end{bmatrix}$$

Обычная векторная жизнь. Но в обществе таких векторов существуют особые представители, которые обладают внутренним стержнем и не желают изменять себе в трудные минуты.

Возьмём вектор:

$$v = \begin{bmatrix} -1 \\ 2 \end{bmatrix}$$

Выполним умножение:

$$A v = \begin{bmatrix} 2 & 6 \\ -1 & -1 \end{bmatrix} \begin{bmatrix} -1 \\ 2 \end{bmatrix} = \begin{bmatrix} 2(-1) + 6(2) \\ -1(-1) -1(2) \end{bmatrix} = \begin{bmatrix} -2 + 12 \\ 1 - 2 \end{bmatrix} = \begin{bmatrix} 10 \\ -1 \end{bmatrix}$$

На последнем шаге вынесли константу:

$$A v = 2 \cdot \begin{bmatrix} -1 \\ 2 \end{bmatrix}$$

Что произошло?
В результате умножения матрицы $A$ на вектор $v$, данный вектор «восстал из пепла» с числовым коэффициентом $\lambda = 2$.
Это и есть собственный вектор с соответствующим собственным значением.

Собственные вектора и числа

Пусть $A$ – квадратная матрица $n$-го порядка.
Ненулевой столбец

$$x = \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix}$$

удовлетворяющий условию

$$A \cdot x = \lambda \cdot x, \quad (6.1)$$

называется собственным вектором матрицы $A$.
Число $\lambda$ в равенстве (6.1) называется собственным значением матрицы $A$.
Говорят, что собственный вектор $x$ соответствует (или принадлежит) собственному значению $\lambda$.

Поставим задачу нахождения собственных значений и собственных векторов матрицы.
Определение (6.1) можно записать в виде:

$$(A - \lambda E) \cdot x = 0,$$

где $E$ – единичная матрица $n$-го порядка.
Таким образом, условие (6.1) представляет собой однородную систему $n$ линейных алгебраических уравнений с $n$ неизвестными $x_1, x_2, \dots, x_n$:

$$\begin{cases} a_{11} x_1 + a_{12} x_2 + \dots + a_{1n} x_n - \lambda x_1 = 0, \\ a_{21} x_1 + a_{22} x_2 + \dots + a_{2n} x_n - \lambda x_2 = 0, \\ \vdots \\ a_{n1} x_1 + a_{n2} x_2 + \dots + a_{nn} x_n - \lambda x_n = 0. \end{cases} \quad (6.2)$$

Так как нас интересуют нетривиальные решения ($x \neq 0$) однородной системы, то определитель матрицы системы должен быть равен нулю:

$$\det(A - \lambda E) = \begin{vmatrix} a_{11} - \lambda & a_{12} & \dots & a_{1n} \\ a_{21} & a_{22} - \lambda & \dots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \dots & a_{nn} - \lambda \end{vmatrix} = 0. \quad (6.3)$$

В противном случае, по правилу Крамера, система имеет единственное тривиальное решение $x = 0$.

Задача нахождения собственных значений матрицы свелась к решению уравнения:

$$\det(A - \lambda E) = \begin{vmatrix} a_{11} - \lambda & a_{12} & \dots & a_{1n} \\ a_{21} & a_{22} - \lambda & \dots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \dots & a_{nn} - \lambda \end{vmatrix} = 0,$$

которое называется характеристическим уравнением матрицы $A$.
- Корни характеристического многочлена (характеристического уравнения (6.3)) и только они являются собственными значениями матрицы.
- По основной теореме алгебры характеристическое уравнение имеет $n$ (в общем случае комплексных) корней (с учетом их кратностей).
- Собственные значения и собственные векторы существуют у любой квадратной матрицы.
- Собственные значения матрицы определяются однозначно (с учетом их кратности),
а собственные векторы — неоднозначно.
- Совокупность всех собственных значений матрицы (с учетом их кратностей) называется спектром матрицы.
- Спектр матрицы называется простым, если собственные значения матрицы попарно различны (все корни характеристического уравнения простые).

Свойства собственных векторов

Пусть $A$ – квадратная матрица $n$-го порядка.

1. Собственные векторы, соответствующие различным собственным значениям, линейно независимы.
2. Ненулевая линейная комбинация собственных векторов, соответствующих одному собственному значению, является собственным вектором, соответствующим тому же собственному значению.

Алгоритм нахождения собственных векторов и собственных значений матрицы

Для нахождения собственных значений и собственных векторов квадратной матрицы
$A$ порядка $n$ необходимо выполнить следующие шаги:

1. Составить характеристический многочлен матрицы:

$$\Delta_A (\lambda) = \det(A - \lambda E).$$

1. Найти все различные корни $\lambda_1, \dots, \lambda_k$
   характеристического уравнения $\Delta_A (\lambda) = 0$.
   Кратности корней $n_1, n_2, \dots, n_k$ (где $n_1 + n_2 + \dots + n_k = n$)
   определять не нужно.

2. Для каждого собственного значения $\lambda = \lambda_1$
   найти фундаментальную систему решений $\varphi_1, \varphi_2, \dots, \varphi_{n - r}$
   однородной системы уравнений:

$$(A - \lambda E) \cdot x = 0.$$

Здесь $r = \operatorname{rg}(A - \lambda_1 E)$.
Для решения этой системы можно использовать стандартные методы нахождения
фундаментальной матрицы.

1. Записать линейно независимые собственные векторы матрицы $A$,
   отвечающие собственному значению $\lambda_1$:

$$s_1 = C_1 \cdot \varphi_1, \quad s_2 = C_2 \cdot \varphi_2, \quad \dots, \quad s_{n - r} = C_{n - r} \cdot \varphi_{n - r},$$

где $C_1, C_2, \dots, C_{n - r}$ – произвольные ненулевые постоянные.

Совокупность всех собственных векторов, отвечающих $\lambda_1$,
образуют ненулевые столбцы вида:

$$s = C_1 \cdot \varphi_1 + C_2 \cdot \varphi_2 + \dots + C_{n - r} \cdot \varphi_{n - r}.$$

В дальнейшем собственные векторы будем обозначать буквой $s$.

1. Повторить шаги 3 и 4 для остальных собственных значений $\lambda_2, \dots, \lambda_k$.

Пример расчета

Найти собственные значения и собственные векторы матрицы

$$A = \begin{pmatrix} 1 & -2 \\ 3 & 8 \end{pmatrix}.$$

1. Нахождение собственных значений

Сначала составим характеристический многочлен матрицы:

$$\Delta(\lambda) = \det(A - \lambda E) = \det \begin{pmatrix} 1 - \lambda & -2 \\ 3 & 8 - \lambda \end{pmatrix}.$$

Вычислим определитель:

$$\Delta(\lambda) = (1 - \lambda)(8 - \lambda) - (-2)(3) = (1 - \lambda)(8 - \lambda) + 6.$$

Раскроем скобки:

$$(1 - \lambda)(8 - \lambda) = 8 - \lambda - 8\lambda + \lambda^2 = \lambda^2 - 9\lambda + 8.$$

Таким образом:

$$\Delta(\lambda) = \lambda^2 - 9\lambda + 8 + 6 = \lambda^2 - 9\lambda + 14.$$

Приравниваем характеристический многочлен к нулю:

$$\lambda^2 - 9\lambda + 14 = 0.$$

Вычислим дискриминант:

$$D = (-9)^2 - 4 \cdot 1 \cdot 14 = 81 - 56 = 25.$$

Находим собственные значения:

$$\lambda = \frac{9 \pm \sqrt{25}}{2} = \frac{9 \pm 5}{2}.$$

Отсюда:

$$\lambda_1 = \frac{9 + 5}{2} = 7, \quad \lambda_2 = \frac{9 - 5}{2} = 2.$$

1. Нахождение собственных векторов

Для $\lambda_1 = 7$

Найдем собственный вектор $v_1$, решая систему:

$$(A - 7E) \cdot x = 0 \quad \Longrightarrow \quad \begin{pmatrix} 1 - 7 & -2 \\ 3 & 8 - 7 \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix}.$$

Упрощаем матрицу:

$$\begin{pmatrix} -6 & -2 \\ 3 & 1 \end{pmatrix}.$$

Запишем систему уравнений:

$$\begin{cases} -6x_1 - 2x_2 = 0, \\ 3x_1 + x_2 = 0. \end{cases}$$

Из второго уравнения:

$$x_2 = -3x_1.$$

Выберем $x_1 = 1$ (произвольная ненулевая величина), тогда $x_2 = -3$. Таким образом, собственный вектор:

$$v_1 = \begin{pmatrix} 1 \\ -3 \end{pmatrix} \quad (\text{с точностью до произвольного множителя}).$$

Для $\lambda_2 = 2$

Найдем собственный вектор $v_2$, решая систему:

$$(A - 2E) \cdot x = 0 \quad \Longrightarrow \quad \begin{pmatrix} 1 - 2 & -2 \\ 3 & 8 - 2 \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix}.$$

Упрощаем матрицу:

$$\begin{pmatrix} -1 & -2 \\ 3 & 6 \end{pmatrix}.$$

Запишем систему уравнений:

$$\begin{cases} -x_1 - 2x_2 = 0, \\ 3x_1 + 6x_2 = 0. \end{cases}$$

Из первого уравнения:

$$x_1 = -2x_2.$$

Выберем $x_2 = 1$, тогда $x_1 = -2$. Таким образом, собственный вектор:

$$v_2 = \begin{pmatrix} -2 \\ 1 \end{pmatrix} \quad (\text{с точностью до произвольного множителя}).$$

Итог

Собственные значения:

$$\lambda_1 = 7, \quad \lambda_2 = 2.$$

Собственные векторы:

$$v_1 = \begin{pmatrix} 1 \\ -3 \end{pmatrix}, \quad v_2 = \begin{pmatrix} -2 \\ 1 \end{pmatrix}.$$