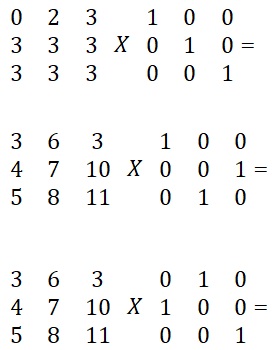Лекция 2 Базис линейного пространства. Координаты и преобразования координат в линейном пространстве

Чтобы продолжить разговор необходимо доказать, что множество матриц образуют линейное пространство. Рассмотрим подробнее операции.

Презентация доступна здесь

Линейные операции над матрицами

Рассмотрим важные математические объекты — матрицы.
Матрицей размером m × n называется совокупность m · n чисел, расположенных в виде прямоугольной таблицы из m строк и n столбцов:

A = $$\begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{pmatrix}$$

или A = $$(a_{ij})$$ , i = 1, ..., m; j = 1, ..., n.

Числа, составляющие матрицу, называются элементами матрицы:
$$a_{ij}$$
— элемент матрицы, стоящий на пересечении $i$-й строки и $j$-го столбца матрицы.
Всюду далее предполагается, что элементы матриц являются действительными числами, если не оговорено противное.

Пример 1.1. Определить размеры матриц:

A = $$\begin{pmatrix} 1 & 0 \\ 2 & 3 \\ 4 & 2 \end{pmatrix}$$ ,
B = $$\begin{pmatrix} 1 & 0 & 4 & 2 \\ 3 & 6 & 8 & 1 \end{pmatrix}$$ ,
c = $$\begin{pmatrix} 1 & 2 & 3 \end{pmatrix}$$ ,
d = $$\begin{pmatrix} 1 \\ 2 \end{pmatrix}$$

Решение. Матрица A имеет размеры 3 × 2, а матрица B — 2 × 4, c — 1 × 3, d — 2 × 1.

Две матрицы $A$ и $B$ называются равными ($A = B$), если они имеют одинаковые размеры ($m \times n$) и равные соответствующие элементы:
$$a_{ij} = b_{ij}, i = 1, \dots, m; j = 1, \dots, n.$$

Виды матриц

В общем случае матрицу (размеров $m \times n$) называют прямоугольной. В частности, если матрица состоит из одного столбца ($n = 1$) или одной строки ($m = 1$), то она называется матрицей-столбцом или матрицей-строкой (либо просто столбцом или строкой) соответственно. Матрицы-строки или матрицы-столбцы часто обозначают строчными буквами (в примере 1.1: $C$ — строка, $D$ — столбец).
Матрица размеров $1 \times 1$ — это просто число (единственный элемент матрицы).

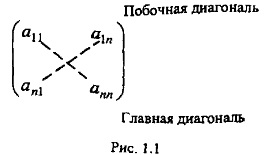
Если у матрицы количество строк ($m$) равно количеству столбцов ($n$), то матрицу называют квадратной ($n$-го порядка).
Элементы
$$a_{11}, a_{22}, \ldots, a_{nn}$$
образуют главную диагональ квадратной матрицы (ей соответствует штриховая линия на рис. 1.1, соединяющая левый верхний угол матрицы $a_{11}$ с правым нижним углом $a_{nn}$).
Диагональ, соединяющая левый нижний угол ($a_{n1}$) с правым верхним углом ($a_{1n}$), называется побочной.

Квадратная матрица вида

$$A = \begin{pmatrix} a_{11} & a_{12} & \dots & a_{1n} \\ a_{21} & a_{22} & \dots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \dots & a_{nn} \end{pmatrix}$$

Матрица, у которой все элементы, стоящие вне главной диагонали, равны нулю, называется диагональной и обозначается
$$\operatorname{diag}(a_{11}, a_{22}, \ldots, a_{nn}).$$

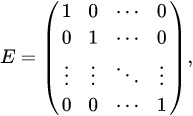
Частным случаем диагональной матрицы служит единичная матрица ($n$-го порядка), которая обозначается $E$ (или $E_n$):
$$E = \begin{pmatrix} 1 & 0 & \dots & 0 \\ 0 & 1 & \dots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \dots & 1 \end{pmatrix}.$$

Сложение матриц

Пусть $A = (a_{ij})$ и $B = (b_{ij})$ — матрицы одинаковых размеров $m \times n$.
Матрица $C = (c_{ij})$ тех же размеров $m \times n$ называется суммой матриц $A$ и $B$,
если ее элементы равны сумме соответствующих элементов матриц $A$ и $B$:

$$c_{ij} = a_{ij} + b_{ij}, \quad i = 1, \ldots, m; \quad j = 1, \ldots, n.$$

Сумма матриц обозначается:
$$C = A + B.$$

Операция сложения матриц определена только для матриц одинаковых размеров и выполняется поэлементно:

Умножение матрицы на число

Произведением матрицы $\mathbf{A} = (a_{ij})$ на число $\lambda$ называется матрица $\mathbf{C} = (c_{ij})$ тех же размеров, что и матрица $\mathbf{A}$, каждый элемент которой равен произведению числа $\lambda$ на соответствующий элемент матрицы $\mathbf{A}$:

$$c_{ij} = \lambda \cdot a_{ij}, \quad i = 1, \dots, m; \quad j = 1, \dots, n.$$

Произведение обозначается λA или Aλ. Операция умножения матрицы на число выполняется поэлементно:

$$\begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{pmatrix} = \begin{pmatrix} \lambda a_{11} & \lambda a_{12} & \cdots & \lambda a_{1n} \\ \lambda a_{21} & \lambda a_{22} & \cdots & \lambda a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ \lambda a_{m1} & \lambda a_{m2} & \cdots & \lambda a_{mn} \end{pmatrix}$$

Умножить на число можно любую матрицу, при этом каждый ее элемент умножается на это число.

Матрица (-1) · A называется противоположной матрицей A и обозначается -A. Сумма матриц B и -A называется разностью матриц и обозначается B - A. Для нахождения разности матриц B - A следует из элементов матрицы B вычесть соответствующие элементы матрицы A. Вычитать можно только матрицы одинаковых размеров.

Свойства линейных операций над матрицами

Операции сложения матриц и умножения матрицы на число называются линейными операциями над матрицами. Непосредственно из определений вытекают следующие свойства линейных операций.

Для любых матриц A, B, C одинаковых размеров и любых чисел α, β справедливы равенства:

1. A + B = B + A (коммутативность сложения);
2. (A + B) + C = A + (B + C) (ассоциативность сложения);
3. существует нулевая матрица O (тех же размеров, что и A): A + O = A;
4. существует матрица -A, противоположная матрице A: A + (-A) = O;
5. α (A + B) = α A + α B;
6. (α + β) A = α A + β A;
7. (α β) A = α (β A);

Умножение матриц

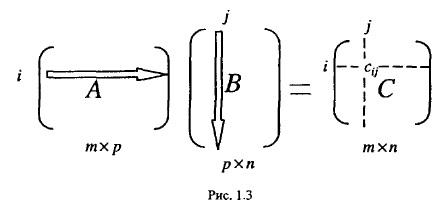
\textbf{Определение произведения матриц.} Пусть даны матрицы $\mathbf{A} = (a_{ij})$ размеров $m \times p$ и $\mathbf{B} = (b_{ij})$ размеров $p \times n$. Матрицу $\mathbf{C}$ размеров $m \times n$, элементы $c_{ij}$, которой вычисляются по формуле:

$$c_{ij} = a_{i1} \cdot b_{1j} + a_{i2} \cdot b_{2j} + \dots + a_{ip} \cdot b_{pj}, \quad i = 1, \dots, m; \quad j = 1, \dots, n,$$

называют произведением матриц $\mathbf{A}$ и $\mathbf{B}$ и обозначают $\mathbf{C} = \mathbf{A} \mathbf{B}$. Операция умножения матрицы $\mathbf{A}$ на матрицу $\mathbf{B}$ определена только для согласованных матриц, у которых число столбцов матрицы $\mathbf{A}$ равно числу строк матрицы $\mathbf{B}$:

$$\underbrace{\mathbf{C}}_{m \times n} = \underbrace{\mathbf{A}}_{m \times p} \cdot \underbrace{\mathbf{B}}_{p \times n}$$

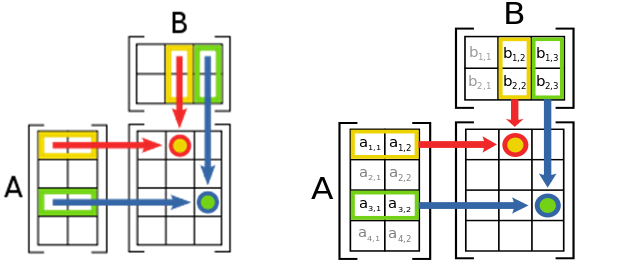
Рассмотрим подробнее процедуру нахождения произведения матриц. Чтобы получить элемент c_{ij}, стоящий на пересечении i-й строки и j-го столбца матрицы C, следует выделить i-ю строку матрицы A и j-й столбец матрицы B (рис. 1.3). Они содержат одинаковое число элементов, так как матрицы A и B согласованы. Затем найти сумму попарных произведений соответствующих элементов: первый элемент i-й строки умножается на первый элемент j-го столбца, второй элемент i-й строки умножается на второй элемент j-го столбца и т.д., а результаты перемножений складываются.

В произведении A · B матрицу A называют левым множителем для B и говорят об умножении матрицы B на матрицу A слева. Аналогично матрицу B называют правым множителем для A и говорят об умножении матрицы A на матрицу B справа.

Пример умножения:

Свойства умножения матриц

Пусть λ — любое число, A, B, C — произвольные матрицы, для которых определены операции умножения и сложения, записанные в левых частях следующих равенств. Тогда определены операции, указанные в правых частях, и справедливы равенства:

1. (AB)C = A(BC); (ассоциативность умножения матриц)
2. A(B + C) = AB + AC; (дистрибутивность умножения)
3. (A + B)C = AC + BC; (дистрибутивность умножения)
4. λ(AB) = (λA)B.

Цветовое пространство, как линейное пространство

Замечательный пример трехмерного линейного пространства дает нам совокупность всех цветов. Под суммой двух цветов будем понимать цвет, образованный их смешением

Под умножением цвета на положительное число k — увеличение в k раз яркости цвета под умножением на (−1) — взятие дополнительного цвета.

Или в виде гифки

Что такое дополнительный цвет?

Дополнительные цвета — пары цветов (тонов хроматического спектра), оптическое смешение которых приводит к формированию психологического ощущения ахроматического тона (чёрного, белого или серого).

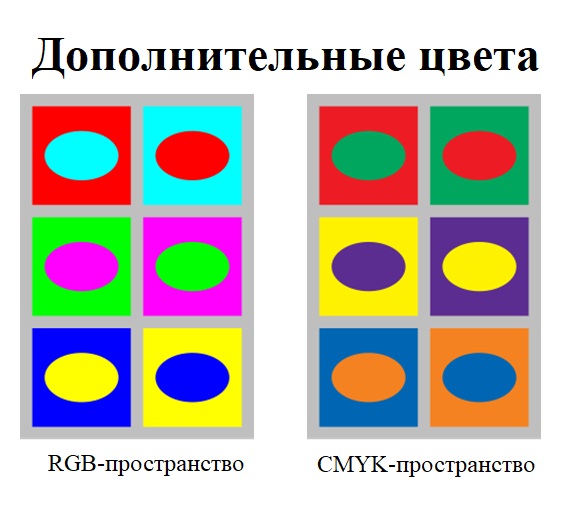
При этом оказывается, что совокупность всех цветов выражается линейно через три цвета: красный, зеленый и синий, т.е. образует трехмерное линейное пространство. (Точнее, некоторое тело в трехмерном пространстве, поскольку яркости цветов ограничены верхним порогом раздражения) Исследование этого трехмерного тела всех цветов является важным орудием цветоведения

Примечание: Строго говоря, сейчас в RGB пространстве любой цвет представим в виде комбинации трех значения Red, Green, Blue. Зададимся вопросом можно ли было выбрать иное сочетание цветов в качестве основы? Ответ - да. Приведем пример другой системы.

CMYK (Cyan, Magenta, Yellow, Key/Black) — это цветовая модель, основанная на использовании четырех цветов. В отличие от RGB, которая используется для отображения цвета на экранах, система CMYK предназначена для печати. В данной модели цвета создаются путем наложения четырех базовых пигментов: голубого (Cyan), пурпурного (Magenta), желтого (Yellow) и черного (Key). Система CMYK работает по принципу субтрактивного смешивания, то есть каждый последующий слой пигмента уменьшает количество света, отражаемого от поверхности.

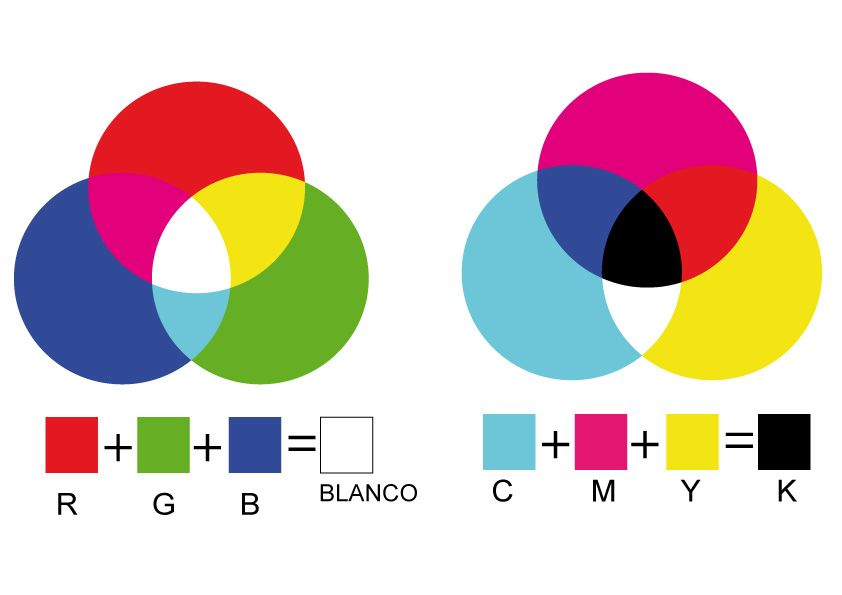
Модель CMYK используется в печати, где цвета создаются путем наложения пигментов. При печати на бумаге важно, чтобы цвета не только правильно отображались, но и давали ожидаемый результат при взаимодействии с белым или не всегда белым фоном (бумагой), поэтому используется система субтрактивного смешивания.

1. Принцип смешивания:
2. RGB — аддитивное смешивание. Световые источники разных цветов (красный, зеленый, синий) комбинируются для создания других цветов.

3. CMYK — субтрактивное смешивание. При наложении пигментов на белую поверхность количество отраженного света уменьшается, что создаёт нужный цвет.

4. Применение:

5. RGB используется для экранов (мониторов, телевизоров, смартфонов), где цвет создается путем изменения интенсивности света.

6. CMYK используется для печати, где смешивание пигментов на поверхности бумаги позволяет добиться нужного цвета.

7. Цветовой диапазон:

8. RGB может создавать яркие и насыщенные цвета, что делает его подходящим для экранов.
9. CMYK ограничен диапазоном печатных красок, что может привести к меньшей насыщенности цветов по сравнению с RGB.

Теперь, когда мы поняли, что системы отсчета могут быть заданы по-разному, попробуем формализировать наш интуитивный опыт.

Линейная зависимость

Линейной комбинацией системы векторов

{X₁, ..., Xₘ}

называется произвольный вектор

α₁ X₁ + ... + αₘ Xₘ

при каких-то фиксированных значениях скаляров α₁, ..., αₘ.

Множество всевозможных линейных комбинаций системы векторов

{X₁, ..., Xₘ}

{α₁ X₁ + ... + αₘ Xₘ | (α₁, ..., αₘ) ⊆ ℝ}

называется линейной оболочкой векторов X₁, ..., Xₘ и обозначается L(X₁, ..., Xₘ). В англоязычной литературе обозначается

span(X₁, ..., Xₘ).

Теорема 1

Линейная оболочка векторов X1,…,Xm образует линейное подпространство пространства V.

Исходя из этого результата, часто о множестве L(X₁, ..., Xₘ) говорят как о подпространстве, натянутом на векторы X₁, ..., Xₘ.

Замечания

1. Один вектор v₁ тоже образует систему: при v₁ = o — линейно зависимую, а при v₁ ≠ o — линейно независимую.

2. Понятия линейной зависимости и линейной независимости для векторов определяются также, как для столбцов матриц. Поэтому все свойства, рассмотренные для столбцов матриц, переносятся на векторы. Применение свойств, доказанных для векторов, к столбцам, можно делать без обоснования, так как множество столбцов является линейным пространством.

Свойства линейно зависимых и независимых n-мерных векторов

1. Если в систему векторов входит нулевой вектор, то она линейно зависима.

2. Если в системе векторов имеется два равных вектора, то она линейно зависима.

3. Если в системе векторов имеется два пропорциональных (коллинеарных) вектора (vᵢ = λ · vⱼ), то она линейно зависима.

4. Система из k > 1 векторов линейно зависима тогда и только тогда, когда хотя бы один из векторов есть линейная комбинация остальных.

5. Любые векторы, входящие в линейно независимую систему, образуют линейно независимую подсистему.

6. Система векторов, содержащая линейно зависимую подсистему, линейно зависима.

7. Если система векторов v₁, v₂, ..., vₖ — линейно независима, а после присоединения к ней вектора v — оказывается линейно зависимой, то вектор v можно разложить по векторам v₁, v₂, ..., vₖ и притом единственным образом, т.е. коэффициенты разложения находятся однозначно.

8. Пусть каждый вектор системы u₁, u₂, ..., uₘ может быть разложен по векторам системы v₁, v₂, ..., vₖ. Тогда, если m > k, то система векторов u₁, u₂, ..., uₘ — линейно зависима.

---

Докажем последнее свойство:

\text{Составим линейную комбинацию векторов } \mathbf{u}_1, \mathbf{u}_2, \dots, \mathbf{u}_m \text{ с коэффициентами } x_1, x_2, \dots, x_m \text{ и приравняем её нулевому вектору:}

$$\sum_{i=1}^{m} x_i \mathbf{u}_i = \mathbf{o}$$

\text{Надо показать, что эта линейная комбинация может быть нетривиальной, т.е. среди коэффициентов } x_i, \, i = 1, \dots, m \text{, можно взять числа, не равные нулю. Подставим в линейную комбинацию разложения векторов } \mathbf{u}_i \text{ по векторам системы } \mathbf{v}_1, \mathbf{v}_2, \dots, \mathbf{v}_k:

$$\mathbf{o} = \sum_{i=1}^{m} x_i \mathbf{u}_i = \sum_{i=1}^{m} x_i \sum_{j=1}^{k} a_{ji} \mathbf{v}_j = \sum_{j=1}^{k} \left( \sum_{i=1}^{m} a_{ji} x_i \right) \mathbf{v}_j$$

\text{Чтобы это равенство выполнялось, достаточно потребовать, чтобы}

$$\sum_{i=1}^{m} a_{ji} x_i = 0, \quad j = 1, \dots, k$$

\text{Таким образом, получаем однородную систему линейных уравнений:}

$$A \mathbf{x} = \mathbf{o}$$

\text{где матрица } A = (a_{ji}) \text{ имеет размеры } k \times m. \text{Поскольку } m > k, \text{то система имеет бесконечно много решений, в том числе и ненулевых. Таким образом, линейная комбинация может быть нетривиальной, и система векторов } \mathbf{u}_1, \mathbf{u}_2, \dots, \mathbf{u}_m \text{ линейно зависима.}

Определения размерности и базиса

Линейное пространство V называется n-мерным, если в нем существует система из n линейно независимых векторов, а любая система из большего количества векторов линейно зависима. Число n называется размерностью (числом измерений) линейного пространства V и обозначается dim V. Другими словами, размерность пространства — это максимальное число линейно независимых векторов этого пространства. Если такое число существует, то пространство называется конечномерным. Если же для любого натурального числа n в пространстве V найдется система, состоящая из n линейно независимых векторов, то такое пространство называют бесконечномерным (записывают: dim V = ∞). Далее, если не оговорено противное, будут рассматриваться конечномерные пространства.

Базисом n-мерного линейного пространства называется упорядоченная совокупность n линейно независимых векторов (базисных векторов).

Теорема о разложении вектора по базису

Если e₁, e₂, ..., eₙ — базис n-мерного линейного пространства V, то любой вектор v ∈ V может быть представлен в виде линейной комбинации базисных векторов:

v = v₁ · e₁ + v₂ · e₂ + ... + vₙ · eₙ

и притом единственным образом, т.е. коэффициенты v₁, v₂, ..., vₙ определяются однозначно. Другими словами, любой вектор пространства может быть разложен по базису и притом единственным образом.

Действительно, размерность пространства V равна n. Система векторов e₁, e₂, ..., eₙ линейно независима (это базис). После присоединения к базису любого вектора v, получаем линейно зависимую систему e₁, e₂, ..., eₙ, v (так как это система состоит из (n+1) векторов n-мерного пространства). По свойству 7 линейно зависимых и линейно независимых векторов получаем заключение теоремы.

Следствие 1.

Если e₁, e₂, ..., eₙ — базис пространства V, то V = Lin(e₁, e₂, ..., eₙ), т.е. линейное пространство является линейной оболочкой базисных векторов.

В самом деле, для доказательства равенства V = Lin(e₁, e₂, ..., eₙ) двух множеств достаточно показать, что включения V ⊂ Lin(e₁, e₂, ..., eₙ) и Lin(e₁, e₂, ..., eₙ) ⊂ V выполняются одновременно. Действительно, с одной стороны, любая линейная комбинация векторов линейного пространства принадлежит самому линейному пространству, т.е. Lin(e₁, e₂, ..., eₙ) ⊂ V. С другой стороны, любой вектор пространства по теореме 8.1 можно представить в виде линейной комбинации базисных векторов, т.е. V ⊂ Lin(e₁, e₂, ..., eₙ). Отсюда следует равенство рассматриваемых множеств.

Следствие 2.

Если e₁, e₂, ..., eₙ — линейно независимая система векторов линейного пространства V и любой вектор v ∈ V может быть представлен в виде линейной комбинации (8.4):
v = v₁ · e₁ + v₂ · e₂ + ... + vₙ · eₙ, то пространство V имеет размерность n, а система e₁, e₂, ..., eₙ является его базисом.

В самом деле, в пространстве V имеется система n линейно независимых векторов, а любая система u₁, u₂, ..., uₙ из большего количества векторов (k > n) линейно зависима, поскольку каждый вектор из этой системы линейно выражается через векторы e₁, e₂, ..., eₙ. Значит, dim V = n и e₁, e₂, ..., eₙ — базис V.

Теорема о дополнении системы векторов до базиса

Теорема о дополнении системы векторов до базиса

Всякую линейно независимую систему **k** векторов **n**-мерного линейного пространства (1 ≤ k < n) можно дополнить до базиса пространства.

В самом деле, пусть e₁, e₂, ..., eₖ — линейно независимая система векторов n-мерного пространства V (1 ≤ k < n). Рассмотрим линейную оболочку этих векторов:

Lₖ = Lin(e₁, e₂, ..., eₖ).

Любой вектор v ∈ Lₖ образует с векторами e₁, e₂, ..., eₖ линейно зависимую систему e₁, e₂, ..., eₖ, v, так как вектор v линейно выражается через остальные. Поскольку в n-мерном пространстве существует n линейно независимых векторов, то Lₖ ≠ V и существует вектор eₖ₊₁ ∈ V, который не принадлежит Lₖ.

Дополняя этим вектором линейно независимую систему e₁, e₂, ..., eₖ, получаем систему векторов e₁, e₂, ..., eₖ, eₖ₊₁, которая также линейно независима. Действительно, если бы она оказалась линейно зависимой, то из пункта 1 замечаний 8.3 следовало, что eₖ₊₁ ∈ Lin(e₁, e₂, ..., eₖ) = Lₖ, а это противоречит условию eₖ₊₁ ∉ Lₖ.

Итак, система векторов e₁, e₂, ..., eₖ, eₖ₊₁ линейно независима. Значит, первоначальную систему векторов удалось дополнить одним вектором без нарушения линейной независимости. Продолжаем аналогично. Рассмотрим линейную оболочку этих векторов:

Lₖ₊₁ = Lin (e₁, e₂, ..., eₖ, eₖ₊₁).

Если Lₖ₊₁ = V, то e₁, e₂, ..., eₖ, eₖ₊₁ — базис и теорема доказана. Если Lₖ₊₁ ≠ V, то дополняем систему e₁, e₂, ..., eₖ, eₖ₊₁ вектором eₖ₊₂ ∉ Lₖ₊₁ и т.д. Процесс дополнения обязательно закончится, так как пространство V конечномерное.

В результате получим равенство V = Lₙ = Lin (e₁, ..., eₖ, ..., eₙ), из которого следует, что e₁, ..., eₖ, ..., eₙ — базис пространства V. Теорема доказана.

Координаты и преобразования координат в линейном пространстве

Пусть $\mathbf{e}_1, \mathbf{e}_2, \dots, \mathbf{e}_n$ — базис линейного пространства $V$.
Каждый вектор $\mathbf{v} \in V$ можно разложить по базису (см. теорему о разложении вектора по базису),
то есть представить в виде:

$$\mathbf{v} = v_1 \mathbf{e}_1 + v_2 \mathbf{e}_2 + \dots + v_n \mathbf{e}_n,$$

причем коэффициенты $v_1, v_2, \dots, v_n$ в разложении определяются однозначно.
Эти коэффициенты называются координатами вектора $\mathbf{v}$ в базисе $\mathbf{e}_1, \mathbf{e}_2, \dots, \mathbf{e}_n$
(или относительно базиса $\mathbf{e}_1, \mathbf{e}_2, \dots, \mathbf{e}_n$).

Координаты $v_1, v_2, \dots, v_n$ вектора $\mathbf{v}$ образуют упорядоченный набор чисел,
который представляется в виде матрицы-столбца:

$$\mathbf{v} = \begin{pmatrix} v_1 \\ \vdots \\ v_n \end{pmatrix},$$

и называется координатным столбцом вектора $\mathbf{v}$ (в данном базисе).
Вектор и его координатный столбец обозначаются одной и той же буквой:
полужирной для вектора и светлой для координат.

Если базис (как упорядоченный набор векторов) представить в виде символической матрицы-строки:

$$(\mathbf{e}) = (\mathbf{e}_1, \dots, \mathbf{e}_n) = \begin{pmatrix} \mathbf{e}_1 & \cdots & \mathbf{e}_n \end{pmatrix},$$

то разложение вектора $\mathbf{v}$ по базису $(\mathbf{e})$ можно записать следующим образом:

$$\mathbf{v} = v_1 \mathbf{e}_1 + v_2 \mathbf{e}_2 + \dots + v_n \mathbf{e}_n = \begin{pmatrix} \mathbf{e}_1 & \cdots & \mathbf{e}_n \end{pmatrix} \begin{pmatrix} v_1 \\ \vdots \\ v_n \end{pmatrix} = (\mathbf{e}) \mathbf{v}.$$

Здесь умножение символической матрицы-строки $(\mathbf{e})$
на числовую матрицу-столбец $\mathbf{v}$ производится по правилам умножения матриц.

При необходимости, если речь идет о разных базисах, у координатного столбца указывается обозначение базиса,
относительно которого получены координаты, например,

$$\mathbf{v}_{sol} = \mathop{\mathbf{v}}\limits_{(\mathbf{e})}$$

— координатный столбец вектора $\mathbf{v}$ в базисе $(\mathbf{e}) = (\mathbf{e}_1, \dots, \mathbf{e}_n)$.

Из теоремы о разложении вектора по базису следует, что равные векторы имеют равные соответствующие координаты
(в одном и том же базисе), и наоборот, если координаты векторов (в одном и том же базисе) соответственно равны,
то равны и сами векторы.

Преобразование координат вектора при замене базиса

Пусть заданы два базиса пространства $V$:
$$(\mathbf{e}) = (\mathbf{e}_1, \mathbf{e}_2, \dots, \mathbf{e}_n), \quad (\mathbf{e}') = (\mathbf{e}'_1, \mathbf{e}'_2, \dots, \mathbf{e}'_n).$$
Базис $(\mathbf{e})$ будем условно называть "старым", а базис $(\mathbf{e}')$ — "новым".
Пусть известны разложения каждого вектора нового базиса по старому базису:

$$\mathbf{e}'_i = s_{1i} \mathbf{e}_1 + s_{2i} \mathbf{e}_2 + \dots + s_{ni} \mathbf{e}_n, \quad i = 1, 2, \dots, n.$$

Записывая по столбцам координаты векторов $(\mathbf{e}'_1, \mathbf{e}'_2, \dots, \mathbf{e}'_n)$ в базисе $(\mathbf{e})$, составляем матрицу:

$$S = \begin{pmatrix} s_{11} & \cdots & s_{1n} \\ \vdots & \ddots & \vdots \\ s_{n1} & \cdots & s_{nn} \end{pmatrix}.$$

Квадратная матрица $S$, составленная из координатных столбцов векторов нового базиса $(\mathbf{e}')$ в старом базисе $(\mathbf{e})$, называется матрицей перехода от старого базиса к новому.
При помощи матрицы перехода формулу можно записать в виде:

$$(\mathbf{e}') = (\mathbf{e}) S$$

или, используя символику:

$$\mathbf{e}' = \mathbf{e} S.$$

Умножение символической матрицы-строки $\mathbf{e}$ на матрицу перехода $S$ производится по правилам умножения матриц.

Пусть в базисе $(\mathbf{e})$ вектор $\mathbf{v}$ имеет координаты $v_1, v_2, \dots, v_n$,
а в базисе $(\mathbf{e}')$ — координаты $v'_1, v'_2, \dots, v'_n$, т.е.

$$\mathbf{v} = v_1 \mathbf{e}_1 + v_2 \mathbf{e}_2 + \dots + v_n \mathbf{e}_n = v'_1 \mathbf{e}'_1 + v'_2 \mathbf{e}'_2 + \dots + v'_n \mathbf{e}'_n.$$

Или, короче:

$$\mathbf{v} = (\mathbf{e}) \mathbf{v} = (\mathbf{e'}) \mathbf{v'}$$

Подставляя в правую часть последнего равенства выражение для $\mathbf{e}'$, получаем:

$$\mathbf{v} = (\mathbf{e}) \mathbf{v} = (\mathbf{e}) S \mathbf{v'}$$

— два разложения вектора $\mathbf{v}$ в одном и том же базисе $(\mathbf{e})$.
Коэффициенты этих разложений должны совпадать (по теореме о разложении вектора по базису), так как это координаты одного и того же вектора в одном базисе. Поэтому:

$$\mathbf{v}_s = S \mathbf{v'}_n$$

или в матричной форме:

$$\begin{pmatrix} v_1 \\ \vdots \\ v_n \end{pmatrix} = \begin{pmatrix} s_{11} & \cdots & s_{1n} \\ \vdots & \ddots & \vdots \\ s_{n1} & \cdots & s_{nn} \end{pmatrix} \begin{pmatrix} v'_1 \\ \vdots \\ v'_n \end{pmatrix}.$$

Дання формула устанавливает связь координат вектора в разных базисах: координатный столбец вектора в старом базисе получается в результате умножения матрицы перехода на координатный столбец вектора в новом базисе.

Домашнее задание

Доказать
1. Теорему "Линейная оболочка векторов X1,…,Xm образует линейное подпространство пространства V."
2. Попрактиковаться в умножени матриц на следующих примерах