Лекция 1 Введение в математические методы обработки и анализа пространственных данных

Пространственный анализ в ГИС упрощает принятие решений во многих сферах, от незначительных ежедневных задач бизнеса до реагирования на глобальные катастрофы. Сложно представить отдельного предпринимателя или крупнейшие отрасли промышленности, которые так или иначе бы не пользовались преимуществами ГИС-картирования.

Пространственный анализ территории помогает определить ее целесообразность для определенных коммерческих целей, обнаружить изменения, отследить тенденции развития событий, оценить риски, предположить последствия и предотвратить ущерб.

В то время как спутники снимают удаленные и труднодоступные регионы, программное обеспечение и методы пространственного анализа обеспечивают обработку данных со скоростью и точностью, которые не под силу ни одному специалисту.

Пространственный Анализ: Что Это Такое?

Пространственный анализ – это процесс интерпретации ГИС-данных, их изучение и моделирование, от получения данных до понимания результатов. Полученную информацию обрабатывают с помощью компьютерных программ для пространственного анализа геоданных и классифицируют по количеству и сложности задач. Самый простой способ – это визуализация, а более глубокий подход предполагает комплексную аналитику с помощью специальных инструментов, которая помогает сделать важные практические выводы.

Примеры анализа пространственных данных ГИС включают измерение расстояний и форм, проложение маршрутов и отслеживание перевозок, установку взаимосвязи между объектами, событиями, территориями методом соотнесения их местоположения с точкой на географической карте (как текущие, так и исторические данные).

Ключевые этапы пространственного анализа

Пространственный анализ представляет собой структурированный процесс, включающий три ключевых этапа: описание, исследование и объяснение.

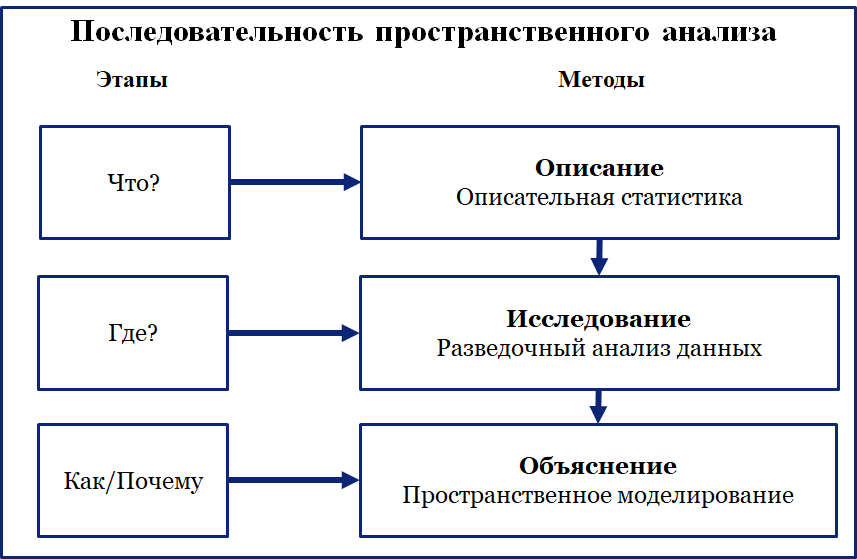
Что мы знаем об исходных данных?

На первом этапе анализа данных ДЗЗ используется описательная статистика, которая позволяет обобщить характеристики полученных данных, оценить их распределение, диапазон значений, а также наличие выбросов и аномалий. Этот этап помогает ответить на вопросы «что?», например:
- Каков средний уровень загрязнения воздуха в определенном регионе?
- Каковы значения индекса растительности на различных участках местности?

Для корректности анализа необходимо убедиться, что данные собраны качественно и правильно откалиброваны. Это критически важно для дальнейшего анализа, так как некорректно обработанные или низкокачественные данные могут исказить результаты.

Рекомендации:
- Проверка точности спутниковых данных, верификация и калибровка сенсоров, исправление геометрических и радиометрических искажений.
- Указание всех характеристик данных, таких как временные интервалы съемки, методы обработки и источники данных.

Где мы проводим исследование (для какой территории?)

На втором этапе применяется исследовательский анализ пространственных данных (Exploratory Spatial Data Analysis, ESDA), который позволяет выявить пространственные закономерности, аномалии и автокорреляции. В контексте ДЗЗ этот этап направлен на изучение пространственного распределения объектов на Земле, что позволяет ответить на вопросы «где?», например:
- Какие районы характеризуются высокой плотностью растительности, а какие — деградацией экосистем?
- Где в регионе можно наблюдать концентрацию загрязненных водоемов, а где самих источников загрязнения?
- Какие области демонстрируют значимые коллебания в уровне осадков?

Методы, используемые на этом этапе, включают пространственное кластерирование, построение карт плотности и анализ пространственной автокорреляции. Применяя эти методы, исследователи могут находить группы сходных объектов или аномальные участки, которые требуют дальнейшего изучения.

Применяемые методы:
- Применение алгоритмов кластеризации для выделения областей с схожими характеристиками.
- Оценка пространственной автокорреляции для анализа связей между соседними участками (например, выявление зон с похожими значениями индекса растительности).
- Визуализация результатов с помощью карт и тепловых карт для выявления пространственных паттернов.

Интерпретация, обобщение данных в модель

На заключительном этапе применяется пространственное моделирование для объяснения причинно-следственных связей между различными явлениями. В этом контексте модели позволяют исследовать, как различные природные и антропогенные факторы влияют на изменения на Земле. Это позволяет ответить на вопросы «почему?» и «как?», например:
- Почему уровень загрязнения в определенных районах растет быстрее, чем в других?
- Как изменяются экосистемы при изменении климата, и как это связано с расположением этих экосистем?
- Какие факторы влияют на динамику лесных пожаров или изменение уровня воды в реках?

Этот этап включает использование более сложных методов статистического анализа, таких как пространственная регрессия и пространственная эконометрика, которые позволяют не только выявить корреляции, но и объяснить, какие факторы приводят к наблюдаемым изменениям.

Методы на этом этапе:
- Использование пространственной регрессии для анализа факторов, влияющих на изменение вегетации, уровня воды, температуры и других переменных.емах.
- Использование методов машинного обучения для предсказания будущих изменений на основе текущих данных.

Кроме того, на этом этапе также рассматриваются дополнительные вопросы:
- Можно ли применить аналогичную методологию к данным других регионов или для других типов спутниковых снимков?
- Как полученные результаты могут быть использованы для разработки рекомендаций по охране окружающей среды или устойчивому развитию?

Данные ДЗЗ в контексте пространственных данных

Радары и лазеры давно перестали быть просто захватывающими атрибутами фантастических кинофильмов, как это было десятки лет назад. Данные инновации широко используются для дистанционного зондирования Земли (ДЗЗ) с тех пор, как наука сделала гигантский шаг вперед. С течением времени, дистанционное зондирование Земли из космоса нашло применение в различных сферах деятельности человека. Например, фермеры ежедневно пользуются преимуществами дистанционного зондирования в сельском хозяйстве. Многие важные решения принимаются с использованием данных RADARSAT, TerraSAR-X, SRTM, EOSDA, ERS, Sentinel, Landsat и других спутников ДЗЗ.

Основы ДЗЗ

Note

Дистанционное Зондирование Земли [англ. термин - Remote Sensing] это наука и совокупность технологий, которые получают, обрабатывают и интерпретируют информацию о различных объектах земной поверхности без прямого физического контакта с этой поверхностью, - посредством фиксирования отраженной солнечной энергии и излученной тепловой энергии (электромагнитного излучения) от земной поверхности, реализующегося сенсорами, расположенными на орбитальных спутниках планеты.

Дистанционное зондирование Земли (ДЗЗ) представляет собой процесс получения информации о поверхности Земли с помощью сенсоров, установленных на орбитальных спутниках, с использованием электромагнитного излучения.

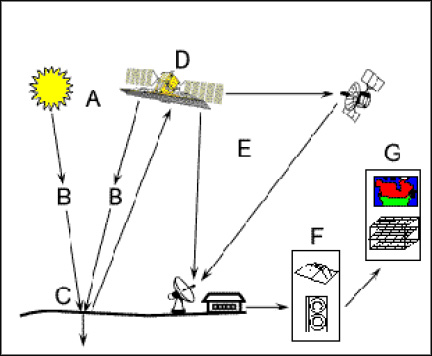
Этот процесс можно разбить на несколько этапов:

1. Источник электромагнитной радиации (Солнце)
   Солнечное излучение является основным источником энергии для большинства методов дистанционного зондирования Земли.

2. Прохождение солнечной радиации через Атмосферу
   Солнечное излучение взаимодействует с атмосферой Земли, частично поглощаясь и рассеиваясь. Некоторые части излучения достигают поверхности планеты.

3. Отражение и испускание электромагнитного излучения от земной поверхности
   Часть солнечного излучения, достигнув поверхности Земли, отражается или испускается обратно в атмосферу. Разные объекты на поверхности Земли отражают и испускают излучение по-разному, в зависимости от их физических свойств.

4. Фиксирование отраженной и испущенной энергии сенсором орбитального спутника
   Сенсоры на спутниках фиксируют отраженную и испущенную энергию, которая затем сохраняется в специальном формате для дальнейшей обработки.

5. Передача и первичная обработка полученных данных
   Полученные данные передаются на Землю, где они проходят первичную обработку для улучшения качества и устранения искажений, вызванных атмосферными и другими факторами.

6. Анализ данных
   На этом этапе данные анализируются с различными целями: картирование, мониторинг, исследование природных явлений, а также для принятия решений в области экологии, сельского хозяйства, городского планирования и других областях.

7. Конечное применение полученных результатов
   Результаты анализа могут использоваться для разработки карт, написания научных статей, принятия управленческих решений и в других практических целях.

Физические принципы ДЗЗ

Основным источником электромагнитного излучения является Солнце. Прежде чем солнечное излучение достигнет Земли, оно должно пройти через атмосферу. Выделяют три основных типа взаимодействия излучения с атмосферой: поглощение, перенос и рассеивание. Излучение, прошедшее через атмосферу, затем отражается или поглощается земной поверхностью

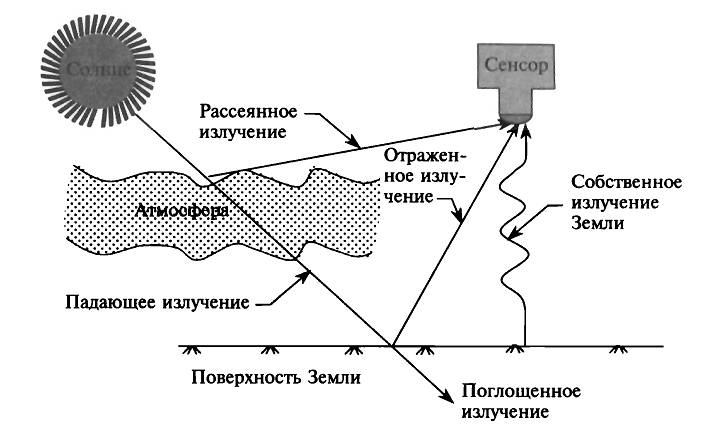
При распространении электромагнитного излучения через атмосферу оно частично поглощается молекулами различных газов. Наибольшей способностью к поглощению солнечного излучения обладают озон (О3), пары воды (Н20) и углекислый газ (С02). На рис показана кривая прозрачности атмосферы в диапазоне длин волн от 0 до 22 мкм.

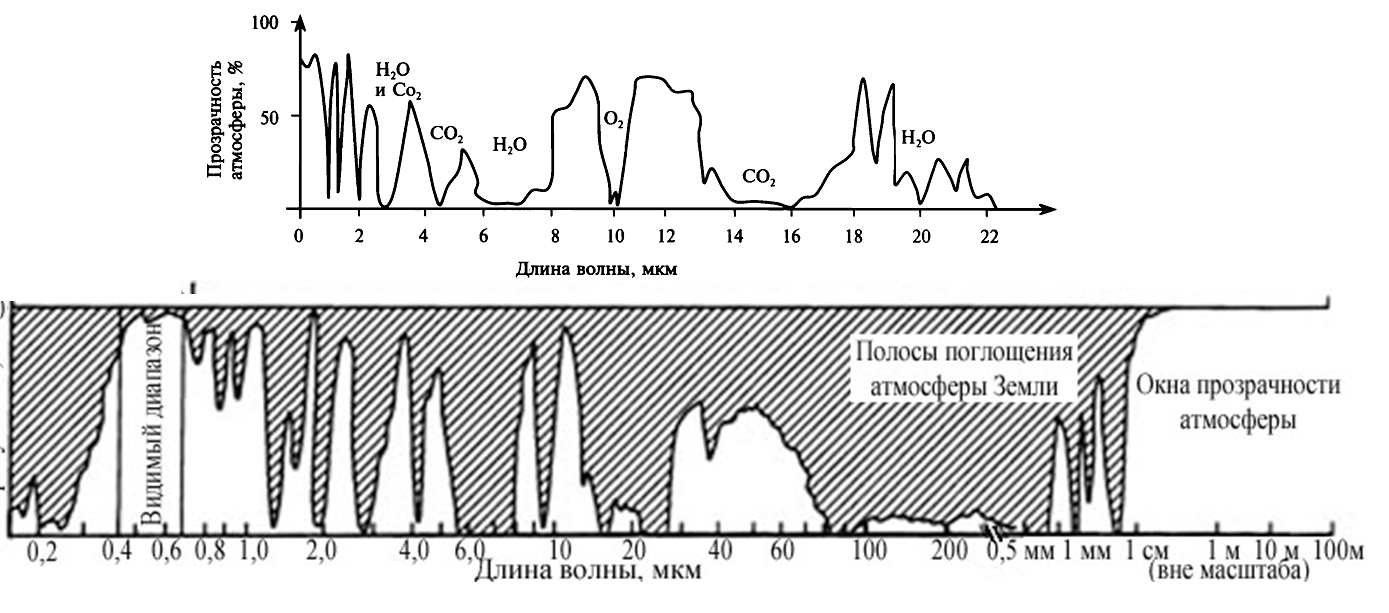
Видно, что примерно половина этого спектрального диапазона является совершенно бесполезной с точки зрения дистанционного зондирования земной поверхности, просто потому, что соответствующее излучение не может пройти через атмосферу. Для дистанционного зондирования используют только те диапазоны длин волн, которые лежат вне основных интервалов поглощения. Такие диапазоны называются окнами прозрачности атмосферы (отображены на графике белым цветом). Они представляют собой такие участки спектра электромагнитного излучения, которые не поглощаются атмосферой. При съемке поверхности Земли из космоса учитывают этот факт, а потому, съемку проводят только в окнах прозрачности.

Окно прозранчости атмосферы

Окно прозрачности атмосферы — это диапазон частот или длин волны, при которой наблюдается минимальное рассеивание и поглощение света, или, другими словами, минимальное затухание волны.

1. "Большое окно": 0,3–1,3 мкм (видимый диапазон)
2. 1,5–1,8 мкм (инфракрасный диапазон)
3. 2,0–2,6 мкм (инфракрасный диапазон)
4. 7,0–15,0 мкм (тепловой инфракрасный диапазон)
5. 0,5 мм и более 10 м (микроволновый и радиодиапазон - наибольшая прозрачность)

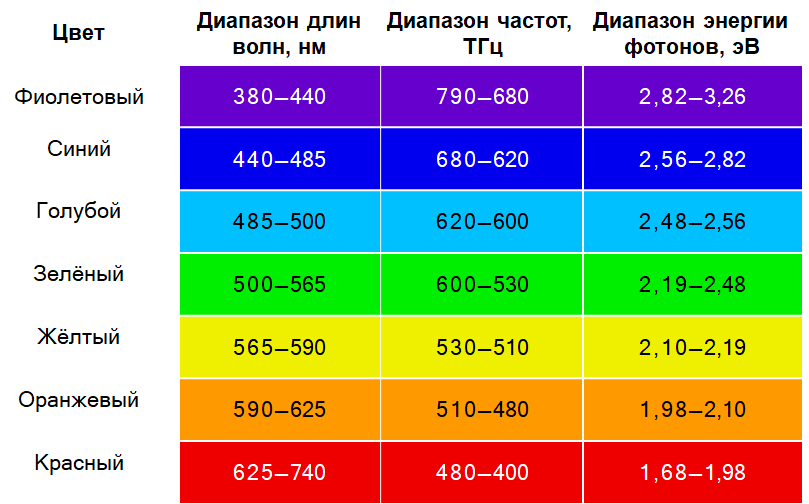
В атмосфере также происходит рассеивание лучей. Атмосферная дымка (эффект рассеивания лучей) наиболее сильно проявляется в синей, голубой зонах спектра (0,38 - 0,5 мкм). Она снижает контраст изображения, искажает цвет объектов. Поэтому в современном дистанционном зондировании при съемки поверхности Земли голубой диапазон не используется.

Диапазоны видимого излучения

Диапазоны инфракрасного излучения

Аббревиатура	Длина волны	Характеристика
NIR	0.75–1.4 мкм	Определяется по поглощению электромагнитного излучения водой и обычно используется в оптоволокне из-за низких потерь затухания в стекле. Усилители яркости изображения чувствительны к этой области спектра. Пример: прибор ночного видения.
SWIR	1.4–3 мкм	Поглощение электромагнитного излучения водой значительно возрастает при 1450 нм. Диапазон 1530–1560 нм преобладает в области дальней связи.
MWIR	3–8 мкм	Диапазон 3–5 мкм соответствует выбросу реактивного двигателя самолета, что позволяет делать самонаводящиеся ракеты.
LWIR	8–15 мкм	Диапазон, в котором датчики могут получить полностью пассивное изображение на основе тепловых выбросов, не требуя освещения, такого как солнце, луна или инфракрасный осветитель.
FIR	15–1000 мкм

Модель данных ДЗЗ

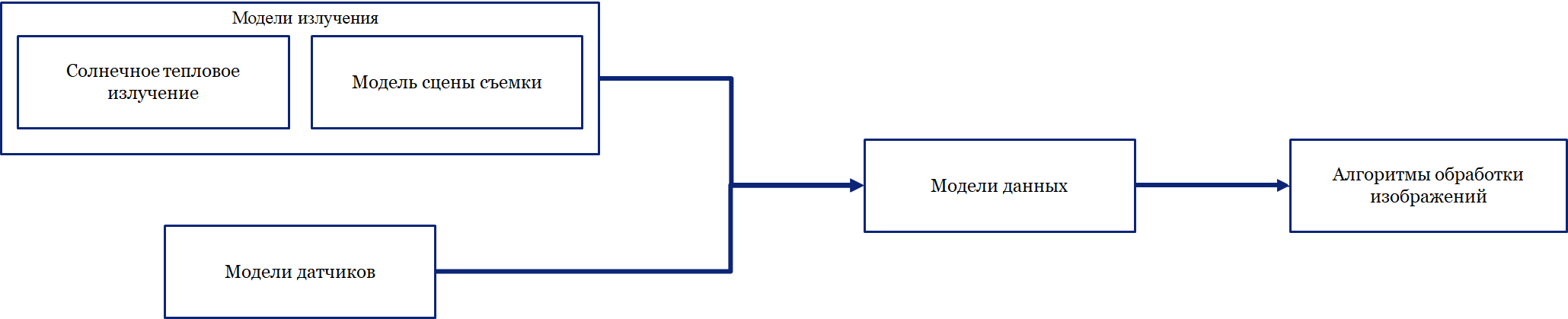
При интерпретации космических снимков их часто рассматривают как обычный набор данных, без какой-либо привязки к тем физическим процессам, которые послужили источником этих данных. Это распространенная ошибка, которая ведет к выбору неоптимальных алгоритмов обработки изображений. Вместе с тем модели данных часто уже содержат определенные характеристики излучения и съемочной аппаратуры, которые можно использовать для учета физических процессов при разработке алгоритмов обработки изображений.

Замечание о форме записи

Материалы дистанционного зондирования Земли (ДЗЗ) требуют специфического подхода к их хранению и обработке, учитывая огромный объем данных и высокую детализацию изображений. Разнообразие форматов и методов хранения может вызвать затруднения при их использовании в междисциплинарных исследованиях. Важно понимать, что для различных типов данных, таких как изображение, спектральные данные или данные о местоположении, существуют разные требования к организации хранения и передачи информации.

Изображения, получаемые с помощью датчиков, представляют собой дискретизированные данные. После того как аналоговый сигнал, регистрируемый датчиком, преобразуется в цифровой формат, данные о каждом пикселе изображения записываются в виде матрицы значений. Эти матрицы могут быть представлены в разных форматах в зависимости от конкретных требований обработки и хранения данных.

Как правило, данные изображения можно представить в виде матрицы пикселей, где каждый пиксель будет содержать информацию о интенсивности отраженного излучения в определенном диапазоне длин волн. Пиксели изображений ДЗЗ часто сохраняются в виде целых чисел, что позволяет компактно представлять и обрабатывать данные. Важно отметить, что координаты пикселей в матрице могут быть представлены двумя индексами (i, j), где i — номер строки, а j — номер столбца.

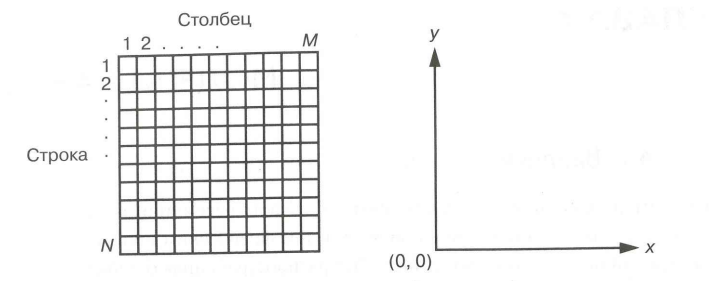
Когда данные ДЗЗ хранятся в цифровом формате, важно учитывать, что для их дальнейшей обработки необходимо сохранить не только значения пикселей, но и информацию о геопривязке снимка, его пространственном разрешении, а также дополнительные метаданные, такие как дата съемки, тип датчика, и другие параметры. Эта информация критична для точной геопространственной интерпретации данных.
Многие системы хранения данных также поддерживают метки времени для каждого пикселя, что позволяет отслеживать изменения в данных за определенные периоды времени.

• Изображения ДЗЗ часто сохраняются в популярных форматах, таких как GeoTIFF или JPEG2000. В случае с GeoTIFF добавляется информация о пространственном расположении пикселей, что позволяет интегрировать изображение с географической информацией. Это очень важно для картографирования, мониторинга изменения земной поверхности и других геопространственных задач.
• Часто для хранения данных ДЗЗ применяются форматы, такие как HDF5 (Hierarchical Data Format), которые позволяют удобно структурировать данные по различным спектральным каналам. Например, спутниковые снимки могут содержать несколько каналов (видимый спектр, инфракрасный спектр и т. д.), каждый из которых должен храниться отдельно, но при этом быть связанным с другими данными для комплексной обработки.

Одномерный статитический анализ (Гистограмма)

Прежде чем приступить к обсуждению методов многомерного статистического анализа многоспектральных изображений, рассмотрим основные понятия одномерного статистического анализа.

Гистограмма характеризует статистическое распределение количества пикселов изображения в зависимости от их значений. Для построения гистограммы $\text{hist}$ достаточно вычислить количество пикселов в каждом интервале значений $DN$, а затем поделить его на общее число пикселов $N$:

$$\text{hist}_p(y) = \frac{\text{количество пикселов}(DN)}{N}$$

Гистограмму часто интерпретируют как известную в статистике функцию плотности вероятности (PDF):

$$\text{hist}_p(y) = \text{PDF}(DN)$$

Однако такая интерпретация математически не совсем корректна, так как функцию плотности вероятности можно определить только для непрерывно распределённых случайных величин, а цифровые изображения редко представляют собой реализацию случайных процессов, не говоря уже о различии непрерывных функций и дискретных наборов данных, из которых состоят эти изображения.

Гистограммы снимков больших областей земной поверхности — унимодальны (т. е. у них имеется только один пик) и характеризуются длинным «хвостом» в области больших значений пикселов. Важно помнить, что гистограмма характеризует распределение числа пикселов в зависимости от их значений, но не их пространственное распределение. Так, например, наличие у гистограммы двух пиков говорит лишь о превалировании двух типов земных покровов (например, воды и почвы), но не о пространственной взаимосвязи соответствующих пикселов. В частности, гистограммы снимков с множеством мелких озер, полученные в ближней инфракрасной зоне, могут почти совпадать с гистограммой снимка прибрежной океанической области в том же спектральном диапазоне.

Гистограмму снимка часто используют для повышения его контрастности. В частности, для этого можно сначала растянуть диапазон значений пикселов, а затем обрезать его с одного или обоих концов гистограммы. Соответствующие пороговые значения можно указать в процентной доле от общего числа пикселов изображения.

Многомерный статитический анализ

Формулы и определения предыдущего раздела легко обобщаются на случай $k$-мерного вектора измерений $DN$:

$$\mathbf{DN} = \left[ DN_1, DN_2, \dots, DN_k \right]$$

Приведённую формулу можно упростить, используя для обозначения пиксела его порядковый номер $p$:

$$\mathbf{d}_N = [DN_1, DN_2, \dots, DN_x]$$

где $DN_p$ представляет собой измерение для пиксела с порядковым номером $p$, а $DN_x$ — это значение для последнего измерения.

Диаграмма рассеяния

Одним из способов графического представления дву- и трёхмерных данных является диаграмма рассеяния. В качестве примера показана диаграмма рассеяния для многоспектрального снимка, полученного по каналам 2, 3 и 4 аппаратуры Sentinel. Точками на этой диаграмме отмечены все ненулевые векторы измерений, вне зависимости от того, сколько пикселов на гистограмме соответствовали каждому из них. В этом отношении диаграмма является бинарной, и по ней нельзя определить, сколько пикселов соответствуют тому или иному вектору.

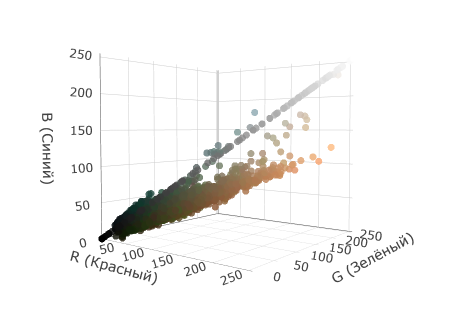
При интерактивном просмотре диаграммы с помощью специального программного обеспечения её можно проецировать на плоскость экрана под разными углами и таким образом увидеть определённые особенности распределения данных в трёхмерном пространстве измерений. В частности, все точки диаграммы можно спроецировать на одну из координатных плоскостей.

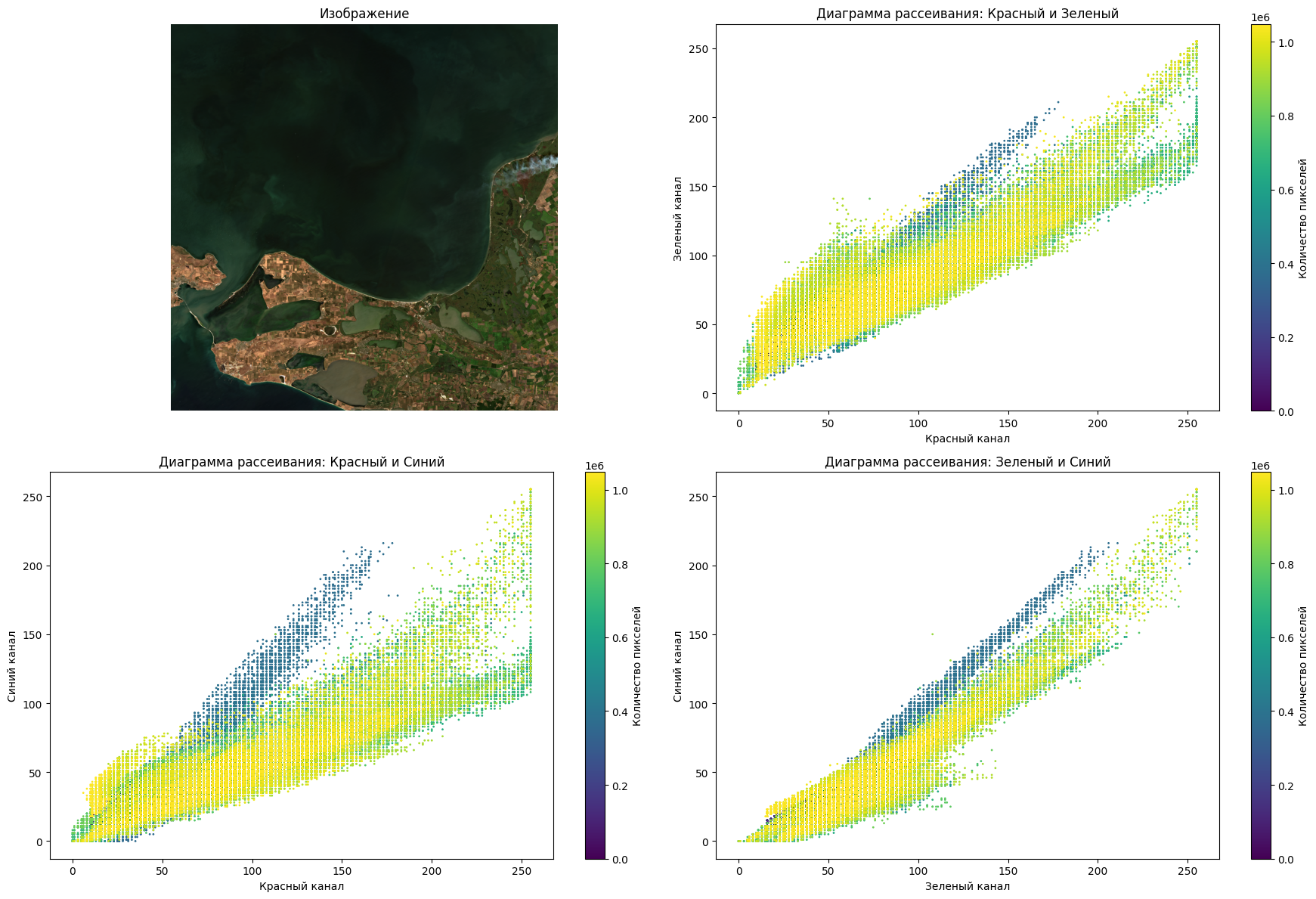
Следует, однако, заметить, что при любом таком проецировании будет теряться часть спектральной информации, поскольку все точки трёхмерной диаграммы, лежащие вдоль одной линии проекции, будут представлены на плоскости одной единственной точкой. Ещё большая потеря информации произойдёт, если тем же способом попытаться получить из двумерной диаграммы рассеяния одномерную гистограмму.

Хотя использование диаграмм рассеяния приводит к существенному снижению количества данных, графическое представление многоспектральных данных может по-прежнему оставаться непростой задачей.

Чтобы протестировать предлашаю вам следующие два изображения, которые вы можете скачать

И загрузить сюда:

Некоторые математические сведения

Линейное (или векторное) пространство — это основополагающий термин, встречающийся, наверное, в подавляющем большинстве работ по высшей математике. Он является необходимым элементом программы по линейной алгебре любого факультета, на котором преподаётся высшая математика. Линейное пространство — одна из тех абстракций, которые ближе к жизни, чем большинство других, и, тем не менее, позволяет нам изучить много свойств самых разнообразных объектов, не вдаваясь в детали.

Прежде чем углубиться в теоретическую сторону, вспомним, что же называлось вектором в школьной геометрии. Грубо говоря, вектор в школе представлял собой некоторую стрелочку, которая имела длину и направление и могла быть приложена к любой точке (например, к началу координат).

Ассортимент действий с векторами был ограничен: мы могли умножить вектор на вещественное число, изменяя его длину и, если число было отрицательным, меняя направление на противоположное, а также сложить его с другим вектором. У каждого вектора существовал обратный (той же длины, но направленный в противоположную сторону) вектор, сумма с которым давала так называемый нулевой вектор. Благодаря этому мы могли вычитать векторы.

Эти свойства векторов справедливы и для двухмерного, и для трёхмерного случая. Но можно ли сделать больше?

Аксиоматическое определение линейного пространства

Оказывается, что этих свойств достаточно, чтобы создать нечто, похожее по поведению на школьные векторы, но выходящее далеко за пределы школьной геометрии. Давайте рассмотрим, что такое векторное пространство в абстрактной форме.

Пусть $V$ — это непустое множество, на котором определены две операции:
1. Сложение векторов (если $a, b \in V$, то $a + b \in V$),
2. Умножение векторов на вещественные числа (если $a \in V$ и $\alpha \in \mathbb{R}$, то $\alpha a \in V$).

Тогда, чтобы множество $V$ и операции на нём можно было назвать линейным пространством, должны выполняться следующие аксиомы:

1. Ассоциативность сложения векторов:
   $$(a + b) + c = a + (b + c), \quad \forall a, b, c \in V$$

2. Существование нулевого вектора:
   Существует особый вектор $0$, называемый нулевым вектором, такой, что:
   $$a + 0 = 0 + a = a, \quad \forall a \in V$$

3. Существование обратного вектора:
   Для любого вектора $a \in V$ существует вектор $b \in V$, такой что:
   $$a + b = b + a = 0$$

4. Коммутативность сложения векторов:
   $$a + b = b + a, \quad \forall a, b \in V$$

5. Ассоциативность умножения на скаляр:
   $$\alpha (\beta a) = (\alpha \beta) a, \quad \forall \alpha, \beta \in \mathbb{R}, a \in V$$

6. Дистрибутивность относительно сложения скаляров:
   $$(\alpha + \beta) a = \alpha a + \beta a, \quad \forall \alpha, \beta \in \mathbb{R}, a \in V$$

7. Дистрибутивность относительно сложения векторов:
   $$\alpha (a + b) = \alpha a + \alpha b, \quad \forall \alpha \in \mathbb{R}, a, b \in V$$

8. Умножение на единицу:
   $$1 \cdot a = a, \quad \forall a \in V$$

Условия 1-8 называются аксиомами линейного пространства. Знак равенства, поставленный между векторами, означает, что в левой и правой частях равенства представлен один и тот же элемент множества $V$. Такие векторы называются равными.

Проще говоря, у нас есть набор некоторых штук, которые мы умеем складывать и умножать на числа, причём так, как привыкли делать это с обычными геометрическими векторами. Тогда такие штуки тоже можно называть векторами, а множество из них всех будет называться линейным пространством.

В определении линейного пространства операция умножения вектора на число введена для действительных чисел. Такое пространство называют линейным пространством над полем действительных (вещественных) чисел, или, короче, вещественным линейным пространством.

Если в определении вместо поля $\mathbb{R}$ действительных чисел взять поле комплексных чисел $\mathbb{C}$, то получим линейное пространство над полем комплексных чисел, или, короче, комплексное линейное пространство.

В качестве числового поля можно выбрать и поле $\mathbb{Q}$ рациональных чисел, при этом получим линейное пространство над полем рациональных чисел.

Далее, если не оговорено противное, будут рассматриваться вещественные линейные пространства. В некоторых случаях для краткости будем говорить о пространстве, опуская слово «линейное», так как все пространства, рассматриваемые ниже — линейные.

Замечания по аксиомам

1. Коммутативность группы относительно сложения:
   Аксиомы 1-4 показывают, что линейное пространство является коммутативной группой относительно операции сложения. Это означает, что операция сложения векторов удовлетворяет свойствам ассоциативности и коммутативности, а также существует нейтральный элемент — нулевой вектор.

2. Дистрибутивность и ассоциативность умножения на число:
   Аксиомы 5 и 6 определяют дистрибутивность операции умножения вектора на число:

3. Аксиома 5 — дистрибутивность по отношению к операции сложения векторов.
4. Аксиома 6 — дистрибутивность по отношению к операции сложения чисел.

Аксиома 7, иногда называемая законом ассоциативности умножения на число, выражает связь двух операций: умножения вектора на число и умножения чисел между собой. Аксиома 8 определяет унитарность операции умножения вектора на число, что означает, что умножение на единицу не изменяет вектор.

1. Непустота линейного пространства:
   Линейное пространство является непустым множеством, так как обязательно содержит нулевой вектор, который служит нейтральным элементом для операции сложения.

2. Линейные операции:
   Операции сложения векторов и умножения вектора на число называются линейными операциями над векторами. Эти операции составляют основу линейного пространства.

3. Разность векторов:
   Разностью векторов $\mathbf{u}$ и $\mathbf{v}$ называется сумма вектора $\mathbf{u}$ с противоположным вектором $-\mathbf{v}$. Это обозначается как:
   $$\mathbf{u} - \mathbf{v} = \mathbf{u} + (-\mathbf{v}).$$

4. Коллинеарность векторов:
   Два ненулевых вектора $\mathbf{u}$ и $\mathbf{v}$ называются коллинеарными (или пропорциональными), если существует такое число $\lambda$, что:
   $$\mathbf{v} = \lambda \mathbf{u}.$$
   Понятие коллинеарности распространяется на любое конечное число векторов. Нулевой вектор $\mathbf{o}$ считается коллинеарным с любым вектором.

Следствия из аксиом

1. Единственность нулевого вектора:
   В линейном пространстве существует единственный нулевой вектор.

Доказательство: Пусть $\mathbf{o}$ и $\mathbf{o}'$ — два нулевых вектора. По аксиоме 3 получаем два равенства:
$$\mathbf{o}' + \mathbf{o} = \mathbf{o}' \quad \text{или} \quad \mathbf{o} + \mathbf{o}' = \mathbf{o}.$$
Левые части равны по аксиоме 1, следовательно, равны и правые части, т.е. $\mathbf{o} = \mathbf{o}'$.

1. Единственность противоположного вектора:
   В линейном пространстве для любого вектора $\mathbf{v} \in V$ существует единственный противоположный вектор $(-\mathbf{v}) \in V$.

Доказательство: Пусть $\mathbf{v} \in V$ имеет два противоположных вектора $(-\mathbf{v})$ и $(-\mathbf{v})'$. По аксиомам 2, 3 и 4 получаем:
$$(-\mathbf{v})' = (-\mathbf{v})' + \underbrace{\mathbf{v} + (-\mathbf{v})}_{\mathbf{o}} = \underbrace{(-\mathbf{v})' + \mathbf{v}}_{\mathbf{o}} + (-\mathbf{v}) = (-\mathbf{v}).$$

1. Произведение вектора на ноль:
   Произведение произвольного вектора на ноль равно нулевому вектору:
   $$0 \cdot \mathbf{v} = \mathbf{o} \quad \forall \mathbf{v} \in V.$$

2. Произведение нулевого вектора на любое число:
   Произведение нулевого вектора на любое число равно нулевому вектору:
   $$\lambda \cdot \mathbf{o} = \mathbf{o} \quad \forall \lambda \in \mathbb{R}.$$

3. Вектор, противоположный данному вектору:
   Вектор, противоположный данному вектору, равен произведению данного вектора на число $-1$:
   $$(-\mathbf{v}) = (-1) \cdot \mathbf{v} \quad \forall \mathbf{v} \in V.$$

4. Скобки в суммах и произведениях:
   В выражениях вида $\mathbf{a + b + \ldots + z}$ (сумма конечного числа векторов) или $\alpha \cdot \beta \cdot \ldots \cdot \omega \cdot \mathbf{v}$ (произведение вектора на конечное число множителей) можно расставлять скобки в любом порядке, либо вообще не указывать их.

Примеры доказательств

1. Доказательство единственности нулевого вектора:
   Пусть $\mathbf{o}$ и $\mathbf{o}'$ — два нулевых вектора. Тогда по аксиоме 3 получаем равенства:
   $$\mathbf{o}' + \mathbf{o} = \mathbf{o}' \quad \text{или} \quad \mathbf{o} + \mathbf{o}' = \mathbf{o}.$$

Так как левые части равны по аксиоме 1, правые части также равны, т.е. $\mathbf{o} = \mathbf{o}'$.

1. Доказательство единственности противоположного вектора:
   Пусть $\mathbf{v} \in V$ имеет два противоположных вектора $(-\mathbf{v})$ и $(-\mathbf{v})'$. Тогда по аксиомам 2, 3 и 4 получаем:
   $$(-\mathbf{v})' = (-\mathbf{v})' + \underbrace{\mathbf{v} + (-\mathbf{v})}_{\mathbf{o}} = \underbrace{(-\mathbf{v})' + \mathbf{v}}_{\mathbf{o}} + (-\mathbf{v}) = (-\mathbf{v}).$$

Примеры линейных пространств

Нулевое линейное пространство $\{\mathbf{o}\}$

В данном случае множество $V = \{\mathbf{o}\}$, где $\mathbf{o}$ — единственный элемент (нулевой вектор). В качестве числового поля $F$ можно рассматривать любое поле. Операции в этом пространстве определяются следующим образом:
$$\mathbf{o} + \mathbf{o} = \mathbf{o}, \quad \alpha \mathbf{o} = \mathbf{o} \quad \forall \alpha \in F.$$
Легко проверить, что при таких операциях выполняются все аксиомы линейного пространства, следовательно, указанное множество является линейным пространством над полем $F$.

Геометрические пространства $V_1$, $V_2$, $V_3$

Элементами этих пространств являются геометрические векторы, то есть направленные отрезки. Рассмотрим пространство $V_3$, в котором элементы — это геометрические векторы в трехмерном пространстве.

• Геометрический вектор, начало которого находится в точке $A$, а конец — в точке $B$, обозначается $\overrightarrow{AB}$. Два вектора считаются равными, если они сонаправлены и имеют одинаковую длину.
• Удобно считать, что все векторы закреплены в одной точке $O$, называемой полюсом или началом отсчета. В этом случае каждому вектору соответствует точка пространства — его конец. С каждой точкой пространства связан единственный радиус-вектор, начало которого закреплено в полюсе, а конец указывает на эту точку.

Векторы складываются по правилу параллелограмма: суммой двух радиус-векторов называется диагональ параллелограмма, построенного на этих векторах. Векторы можно умножать на вещественные числа. Произведение радиус-вектора на число $\alpha$ означает вектор, длина которого равна длине исходного вектора, умноженной на $|\alpha|$, а направление совпадает с направлением исходного вектора, если $\alpha > 0$, и заменяется на противоположное, если $\alpha < 0$.

Аксиомы линейного пространства (1)–(8) для этого пространства легко проверяются, и, следовательно, $V_3$ является линейным пространством над полем $\mathbb{R}$.

Аналогично, совокупности векторов на плоскости и на прямой, обозначенные как $V_2$ и $V_1$, также являются линейными пространствами над полем $\mathbb{R}$.

Пространство матриц $F^{m \times n}$

Элементами этого пространства являются матрицы размера $m \times n$ с элементами из поля $F$. Операции на этих матрицах — это стандартные операции матричного сложения и умножения матриц на числа из поля $F$.

• Матричное сложение: Сумма двух матриц $A = (a_{ij})$ и $B = (b_{ij})$ размера $m \times n$ определяется как матрица $C = (c_{ij})$, где каждый элемент $c_{ij} = a_{ij} + b_{ij}$.
• Умножение матрицы на число: Умножение матрицы $A = (a_{ij})$ на число $\alpha \in F$ определяется как матрица $B = (\alpha a_{ij})$, где каждый элемент матрицы $B$ получается умножением соответствующего элемента матрицы $A$ на число $\alpha$.

Легко убедиться, что операции матричного сложения и умножения на число удовлетворяют аксиомам линейного пространства. Следовательно, множество $F^{m \times n}$ является линейным пространством над полем $F$.

• Нулевым вектором в этом пространстве является нулевая матрица размера $m \times n$, все элементы которой равны нулю.

Таким образом, пространство матриц $F^{m \times n}$ является линейным пространством над полем $F$.

ДЗк лекции 2

Доказать, что Пространство матриц $F^{m \times n}$ Элементами этого пространства являются матрицы размера $m \times n$ с элементами из поля $F$ является линейным пространством.