Машина Тьюринга#

В 1936 г. Аланом Тьюрингом для уточнения понятия алгоритма был предложен абстрактный универсальный исполнитель. Его абстрактность заключается в том, что он представляет собой логическую вычислительную конструкцию, а не реальную вычислительную машину. Термин «универсальный исполнитель» говорит о том, что данный исполнитель может имитировать любой другой исполнитель. Например, операции, которые выполняют реальные вычислительные машины можно имитировать на универсальном исполнителе. В последствие, придуманная Тьюрингом вычислительная конструкция была названа машиной Тьюринга.

Кроме того, предполагается, что универсальный исполнитель должен уметь доказывать существование или отсутствие алгоритма для той или иной задачи.

В качестве входных данных для машины Тьюринга используются слова, составленные с помощью некоего алфавита, то есть, набора символов.

Результатом работы машины Тьюринга так же являются слова.

Слово, к которому применяется алгоритм, называется входным. Слово, которое получается в результате работы, выходным.

Набор слов, к которым применим алгоритм, называется областью применимости алгоритма.

Описание машины Тьюринга#

Объяснение описания машины Тьюринга#

Машина Тьюринга представляет собой устройство, содержащее пишущую ленту бесконечной длины, разбитую на ячейки а1, а2, …, аn,… . В каждой ячейке может быть записан один и только один символ из входного алфавита машины Тьюринга.

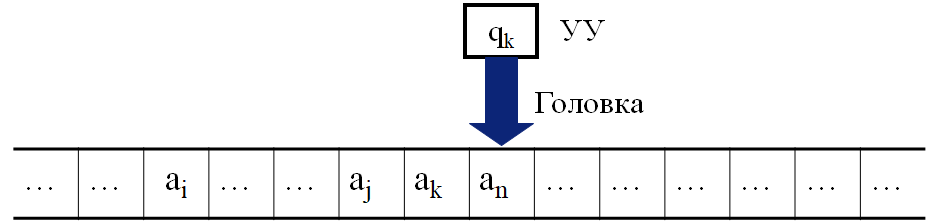
В начальный момент на ленту записывается какое-то слово. Обычно это слово представляет собой описание некоторой задачи, на которых специализируется данная машина Тьюринга. Кроме ленты, у машины имеется читающая-пишущая головка, которая позволяется считать символ из ячейки или записать в ячейку, непосредственно находящуюся под головкой, какой-то один символ. Машина Тьюринга работает по тактам. Такты машины Тьюринга никак не привязываются к единицам времени, например, секундам. Но именно в тактах измеряется “время”, затрачиваемое машиной Тьюринга на то, чтобы выполнить обработку входного слова. Разумно и сложность задачи связывать с числом тактов, которую необходимо затратить на Машине Тьюринга для ее решения.

Управляющее устройство работает согласно правилам перехода, которые представляют алгоритм, реализуемый данной машиной Тьюринга. Каждое правило перехода предписывает машине, в зависимости от текущего состояния и наблюдаемого в текущей клетке символа, записать в эту клетку новый символ, перейти в новое состояние и переместиться на одну клетку влево или вправо. Некоторые состояния машины Тьюринга могут быть помечены как терминальные, и переход в любое из них означает конец работы, остановку алгоритма.

Хотя машина Тьюринга является абстрактной концепцией, достаточно просто представить себе подобную машину (правда, с конечной лентой), и даже существуют демонстрационные машины в таком роде:

Команды для машины Тьюринга удобно представлять в виде таблицы: столбцы таблицы соответствуют текущему (наблюдаемому) символу на ленте, строки – текущему состоянию автомата, а в ячейках записывается команда, которую должен выполнить автомат.

Команда, в свою очередь, может иметь следующую структуру:
$ak, L/R/S, qm$
Сначала идет символ алфавита, который должен быть записан в текущую ячейку ak, затем, указывается перемещение автомата влево (Л), вправо (П) или никуда (остаться на месте, Н). В конце указывается новое состояние, в которое должен перейти автомат qm.

Формальное описание машины Тьюринга#

Машина Тьюринга определяется кортежем вида

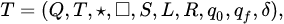
где — конечное множество состояний; — конечный входной алфавит; $\star\notin V$ — символ, называемый маркером начала ленты; $\Box\notin V$ — символ, называемый пустым (или пробелом); $S,L,R\notin V$ — символы, называемые символами направления движения головки; $q_0\in Q$ — начальное состояние; $q_f\in Q$ — заключительное состояние; $\delta$ — функция переходов, являющаяся отображением вида

Функция переходов может быть записана в виде системы команд. Каждая команда есть слово вида

$qa\to rb,M,$

где $a,b\in V\cup{\star,\Box}, M\in{S,L,R},\to\notin V\cup{\star,\Box,S,L,R}$ .

Слово (до стрелки) называется левой частью команды, а слово rb,M (после стрелки) — правой частью команды.

Неформально работу машины Тьюринга можно представить следующим образом. Машина имеет устройство управления, которое может находиться в одном из состояний множества , полубесконечную ленту, разделенную на ячейки, в каждой из которой может быть записан символ из алфавита $V\cup{\star,\Box}$ , причем крайняя левая ячейка хранит символ $\star$ , и головку чтения-записи, которая в каждый момент дискретного времени обозревает какую-то одну ячейку ленты. Символ $\Box$ (пробел) не следует путать с пустой цепочкой — это специальный символ, означающий пустую, т.е. не хранящую символов алфавита $V\cup{\star}$ , ячейку ленты. Команда, записанная выше, разрешает машине Тьюринга, устройство управления которой находится в состоянии , а головка обозревает ячейку, хранящую символ , перевести устройство управления в состояние , записав в обозреваемую ячейку символ (который может и совпадать с ), и оставить головку на прежнем месте, если M=S , сдвинуть ее на одну ячейку влево, если M=L , или на одну ячейку вправо, если M=R .

Таким образом, в отличие от конечных автоматов машина Тьюринга может модифицировать содержимое ленты (т.е. является преобразователем), а также передвигать головку в любом направлении. Впредь условимся говорить о состоянии машины Тьюринга, подразумевая состояние ее устройства управления, и об обозреваемом символе, подразумевая под этим символ той ячейки ленты, которая обозревается в данный момент головкой.

Алфавит машины Тьюринга. Системы счисления#

Как было указано ранее, Алфавитом в машине Тьюринга может быть любое конечное множество символов. Удобнее всего рассматривать в качестве Алфавита некоторую систему счисления.

Система счисления (или система счисления) - это система письма для выражения чисел, то есть математическая нотация для представления чисел данного набора с использованием цифр или других символов последовательным образом.

Системы счисления подразделяются на позиционные и непозиционные, а позиционные, в свою очередь, — на однородные и смешанные.

Непозиционная — самая древняя, в ней каждая цифра числа имеет величину, не зависящую от её позиции (разряда). То есть, если у вас 5 черточек — то число тоже равно 5, поскольку каждой черточке, независимо от её места в строке, соответствует всего 1 один предмет.

Позиционная система — значение каждой цифры зависит от её позиции (разряда) в числе. Например, привычная для нас 10-я система счисления — позиционная. Рассмотрим число 453. Цифра 4 обозначает количество сотен и соответствует числу 400, 5 — кол-во десяток и аналогично значению 50, а 3 — единиц и значению 3. Как видим — чем больше разряд — тем значение выше. Итоговое число можно представить, как сумму 400+50+3=453.

Однородная система — для всех разрядов (позиций) числа набор допустимых символов (цифр) одинаков. В качестве примера возьмем упоминавшуюся ранее 10-ю систему. При записи числа в однородной 10-й системе вы можете использовать в каждом разряде исключительно одну цифру от 0 до 9, таким образом, допускается число 450 (1-й разряд — 0, 2-й — 5, 3-й — 4), а 4F5 — нет, поскольку символ F не входит в набор цифр от 0 до 9.

Смешанная система — в каждом разряде (позиции) числа набор допустимых символов (цифр) может отличаться от наборов других разрядов. Яркий пример — система измерения времени. В разряде секунд и минут возможно 60 различных символов (от «00» до «59»), в разряде часов – 24 разных символа (от «00» до «23»), в разряде суток – 365 и т. д.

Позиционные системы счисления#

Исторически первое изобретение позиционной нумерации, основанной на поместном значении цифр, приписывается шумерам и вавилонянам. Независимо от евразийских цивилизаций двадцатеричную позиционную систему счисления изобрели индейцы майя. В более поздний период такая нумерация была развита индусами и имела неоценимые последствия в истории цивилизации. К числу таких систем относится десятичная система счисления, возникновение которой связано со счётом на пальцах. В средневековой Европе она появилась через итальянских купцов, в свою очередь заимствовавших её у арабов.

Десятичная система счисления#

Это одна из самых распространенных систем счисления. Именно её мы используем, когда называем цену товара и произносим номер автобуса. В каждом разряде (позиции) может использоваться только одна цифра из диапазона от 0 до 9. Основанием системы является число 10.

Для примера возьмем число 503. Если бы это число было записано в непозиционной системе, то его значение равнялось 5+0+3 = 8. Но у нас — позиционная система и значит каждую цифру числа необходимо умножить на основание системы, в данном случае число “10”, возведенное в степень, равную номеру разряда. Получается, значение равно 5*102 + 0*101 + 3*100 = 500+0+3 = 503. Чтобы избежать путаницы при одновременной работе с несколькими системами счисления основание указывается в качестве нижнего индекса. Таким образом, 503 = 50310.

Помимо десятичной системы, отдельного внимания заслуживают 2-, 8-, 16-ая системы.

Двоичная система счисления#

Эта система, в основном, используется в вычислительной технике. Почему не стали использовать привычную нам 10-ю? Первую вычислительную машину создал Блез Паскаль, использовавший в ней десятичную систему, которая оказалась неудобной в современных электронных машинах, поскольку требовалось производство устройств, способных работать в 10 состояниях, что увеличивало их цену и итоговые размеры машины. Этих недостатков лишены элементы, работающие в 2-ой системе. Тем не менее, рассматриваемая система была создана за долго до изобретения вычислительных машин и уходит “корнями” в цивилизацию Инков, где использовались кипу — сложные верёвочные сплетения и узелки.

Двоичная позиционная система счисления имеет основание 2 и использует для записи числа 2 символа (цифры): 0 и 1. В каждом разряде допустима только одна цифра — либо 0, либо 1.

Примером может служить число 101. Оно аналогично числу 5 в десятичной системе счисления. Для того, чтобы перевести из 2-й в 10-ю необходимо умножить каждую цифру двоичного числа на основание “2”, возведенное в степень, равную разряду. Таким образом, число 1012 = 1*22 + 0*21 + 1*20 = 4+0+1 = 510.

Хорошо, для машин 2-я система счисления удобнее, но мы ведь часто видим, используем на компьютере числа в 10-й системе. Как же тогда машина определяет какую цифру вводит пользователь? Как переводит число из одной системы в другую, ведь в её распоряжении всего 2 символа — 0 и 1?

Чтобы компьютер мог работать с двоичными числами (кодами), необходимо чтобы они где-то хранились. Для хранения каждой отдельной цифры применяется триггер, представляющий собой электронную схему. Он может находится в 2-х состояниях, одно из которых соответствует нулю, другое — единице. Для запоминания отдельного числа используется регистр — группа триггеров, число которых соответствует количеству разрядов в двоичном числе. А совокупность регистров — это оперативная память. Число, содержащееся в регистре — машинное слово. Арифметические и логические операции со словами осуществляет арифметико-логическое устройство (АЛУ). Для упрощения доступа к регистрам их нумеруют. Номер называется адресом регистра. Например, если необходимо сложить 2 числа — достаточно указать номера ячеек (регистров), в которых они находятся, а не сами числа. Адреса записываются в 8- и 16-ричной системах (о них будет рассказано ниже), поскольку переход от них к двоичной системе и обратно осуществляется достаточно просто. Для перевода из 2-й в 8-ю число необходимо разбить на группы по 3 разряда справа налево, а для перехода к 16-ой — по 4. Если в крайней левой группе цифр не достает разрядов, то они заполняются слева нулями, которые называются ведущими. В качестве примера возьмем число 1011002. В восьмеричной — это 101 100 = 548, а в шестнадцатеричной — 0010 1100 = 2С16. Отлично, но почему на экране мы видим десятичные числа и буквы? При нажатии на клавишу в компьютер передаётся определённая последовательность электрических импульсов, причём каждому символу соответствует своя последовательность электрических импульсов (нулей и единиц). Программа драйвер клавиатуры и экрана обращается к кодовой таблице символов (например, Unicode, позволяющая закодировать 65536 символов), определяет какому символу соответствует полученный код и отображает его на экране. Таким образом, тексты и числа хранятся в памяти компьютера в двоичном коде, а программным способом преобразуются в изображения на экране.

Восьмеричная система счисления#

8-я система счисления, как и двоичная, часто применяется в цифровой технике. Имеет основание 8 и использует для записи числа цифры от 0 до 7.

Пример восьмеричного числа: 254. Для перевода в 10-ю систему необходимо каждый разряд исходного числа умножить на 8n, где n — это номер разряда. Получается, что 2548 = 2*82 + 5*81 + 4*80 = 128+40+4 = 17210.

Шестнадцатеричная система счисления#

Шестнадцатеричная система широко используется в современных компьютерах, например при помощи неё указывается цвет: #FFFFFF — белый цвет. Рассматриваемая система имеет основание 16 и использует для записи числа: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B. C, D, E, F, где буквы равны 10, 11, 12, 13, 14, 15 соответственно.

В качестве примера возьмем число 4F516. Для перевода в восьмеричную систему — сначала преобразуем шестнадцатеричное число в двоичное, а затем, разбив на группы по 3 разряда, в восьмеричное. Чтобы преобразовать число в 2-е необходимо каждую цифру представить в виде 4-х разрядного двоичного числа. 4F516 = (100 1111 101)2. Но в 1 и 3 группах не достает разряда, поэтому заполним каждый ведущими нулями: 0100 1111 0101. Теперь необходимо разделить полученное число на группы по 3 цифры справа налево: 0100 1111 0101 = 010 011 110 101. Переведем каждую двоичную группу в восьмеричную систему, умножив каждый разряд на 2n, где n — номер разряда: (0*22+1*21+0*20) (0*22+1*21+1*20) (1*22+1*21+0*20) (1*22+0*21+1*20) = 23658.

Пример работы машины Тьюринга#

Допустим, на ленте есть слово, состоящее из символов #, $, 1 и 0. Требуется заменить все символы # и $ на нули. В момент запуска головка находится над первой буквой слова слева. Завершается программа тогда, когда головка оказывается над пустым символом после самой правой буквы слова.
Примечание: длина слова и последовательность символов значения не имеют. На рисунке приводится пример последовательности выполнения команд для конкретного случая. Если на ленте будет другое слово, то и последовательность выполнения команд будет другой. Несмотря на это, данная программа для машины Тьюринга (на рисунке – таблица слева) применима к любым словам описанного внешнего алфавита.

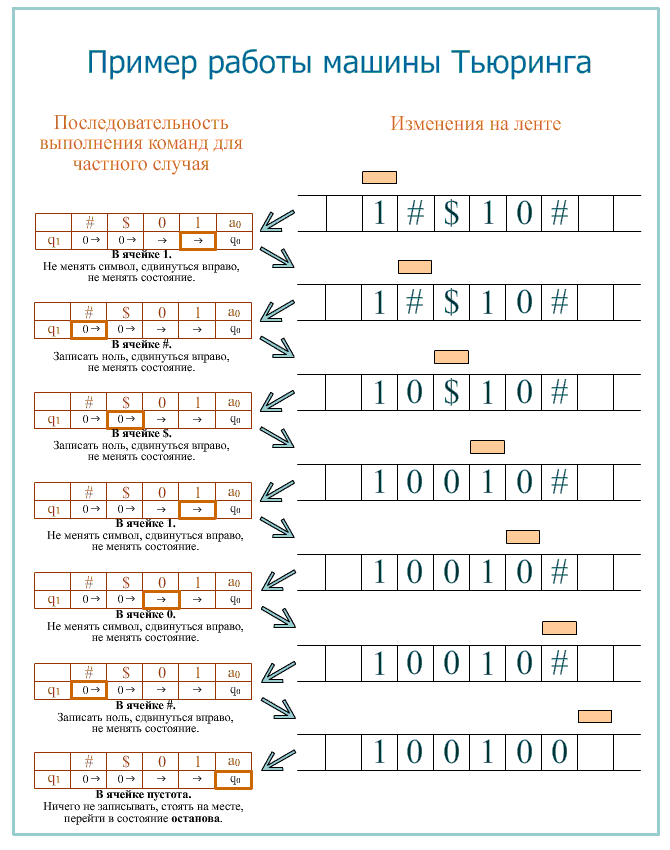
Можно усложнить программу. Допустим, головка располагается не обязательно над первым, а над любым символом слова. Тогда программа для данной машины Тьюринга может быть такой (а могла бы быть и другой):

Здесь происходит сдвиг головки влево до тех пор, пока она не окажется над пустым символом. После этого машина переходит в состояние q2 (команды которого совпадают с командами q1 предыдущей программы).

Алгоритм#

В сегодняшнем социуме слово «алгоритм» настолько широко распространено, что большинству интуитивно понятно. Под ним мы понимаем какую-либо последовательность шагов для достижения той или иной цели. Однако для теоретической науки понятие «алгоритма» достаточно сложное.

Считается, что однозначного определения алгоритма нет, хотя в основном различные источники дают очень близкие определения.

Определения

«Алгоритм — это всякая система вычислений, выполняемых по строго определённым правилам, которая после какого-либо числа шагов заведомо приводит к решению поставленной задачи».

А. Н. Колмогоров

Определения

«Алгоритм — это точное предписание, определяющее вычислительный процесс, идущий от варьируемых исходных данных к искомому результату».

А. А. Марков

Определения

Алгоритм - Конечное множество четко определенных правил, которые задают последовательность действий для выполнения конкретной задачи

ГОСТ Р 51904-2002
Программное обеспечение встроенных систем. Общие требования к разработке и документированию

Свойства алгоритма#

Алгоритм должен быть составлен таким образом, чтобы исполнитель, точно следуя его указаниям, должен получить результат. Это накладывает на указания алгоритма ряд требований, которые называются свойствами алгоритма.
1. Дискретность (прерывность). Алгоритм должен являться упорядоченной совокупностью отделенных друг от друга указаний, образующих дискретную (прерывную) структуру, что предполагает, что два любые последовательные указания при исполнении разделяются ненулевым промежутком времени. Дискретность алгоритма часто подчеркивается нумерацией указаний.
2. Определенность (детерминированность). Алгоритм не может содержать указаний, смысл которых может восприниматься исполнителем неоднозначно или требовать от него свободно принимаемых решений, то есть, одно и то же указание, выполняемое разными исполнителями, должно давать один и тот же результат.
3. Понятность. Алгоритм содержит только те указания (команды), которые входят в СКИ исполнителя этого алгоритма.
4. Массовость. Алгоритм должен быть применим для решения не одной задачи, а для целого класса задач одного типа. В простейшем случае массовость обеспечивает возможность использования различных наборов исходных данных для одной задачи. Если же исходные данные уникальны, то алгоритм в силу свойства определенности будет давать всегда один и тот же результат и само построение алгоритма в этом случае теряет смысл.
5. Результативность (конечность). При точном исполнении всех указаний алгоритма результат решения задачи должен быть получен за конечное число шагов.
6. Формальность. Все указания алгоритма исполнитель должен выполнять формально, не вникая в смысл того, что он делает и даже, возможно, не понимая этого смысла. Очень часто в литературных источниках в качестве примеров алгоритмов приводят рецепты приготовления различных блюд. Но далеко не каждый рецепт является алгоритмом в указанном выше смысле.

В качестве примера рассмотрим рецепт приготовления классической яичницы-глазуньи, который приведен во многих ссылках в Интернете.
1. Раскалить сковородку на сильном огне.
2. Налить на нее масло.
3. Разбить на сковороду яйцо, чтоб не повредить целостность желтка.
4. Уменьшить огонь до среднего.
5. Жарить яйцо, пока белок полностью не побелеет, желток при этом должен остаться сырым.
6. Перед подачей на стол яичницу посолить.

Естественно, пользуясь этими указаниями, практически любой исполнитель, поджарит яичницу, но, только консистенция блюда и его вкус будут у разных исполнителей разным. В приведенной системе почти во всех указаниях нарушено свойство определенности:
- не указано конкретно, каким должен быть сильный огонь – 2000 , 2250 или 2500 ;
- не указано, какое масло налить (соевое, оливковое) и сколько налить: - не указано, до скольких градусов уменьшить огонь;
- не указано, какое количество соли надо использовать.
Поэтому рецепты блюд можно считать алгоритмами лишь условно.

Cвязь Машины Тьюринга и Понятия "Алгоритм"#

Наше воображение в целом допускает существование неразрешимых задач, то есть задач, для решения которых невозможно составить алгоритм.

Исследованием таких задач занимается теория вычислимости.

Примерами алгоритмически неразрешимых задач являются проблема останова и проблема распознавания выводимости. Рассмотрим их более подробно.

Проблема останова

По описанию алгоритма A и входным данным x необходимо выяснить, остановится ли алгоритм A на входных данных x

Проблема останова является алгоритмически неразрешимой. Докажем это.

Пусть существует универсальный алгоритм, решающий проблему останова. Рассмотрим тогда класс алгоритмов, обрабатывающий тексты описания алгоритмов.

В силу существования универсального алгоритма решения проблемы останова, существует алгоритм, который определяет, остановится ли алгоритм из упомянутого класса на собственном тексте, или нет. Обозначим такой алгоритм B.

Построим алгоритм C, входными данными для которого является текст алгоритма A, обрабатывающего свой текст:

Выполнить алгоритм B над A.
Если алгоритм B определил, что A остановится на своем тексте, перейти к шагу 1. Иначе – к шагу 3.
Конец алгоритма C.

Попытавшись применить алгоритм C к алгоритму C, придем к очевидному противоречию: если C остановится на собственном тексте, то он не может остановиться, и наоборот. Следовательно, не существует алгоритма B.

Тезис Чёрча — Тьюринга#

Тезис Чёрча — Тьюринга — это гипотеза, постулирующая эквивалентность между интуитивным понятием алгоритмической вычислимости и строго формализованными понятиями частично рекурсивной функции и функции, вычислимой на машине Тьюринга. В связи с интуитивностью исходного понятия алгоритмической вычислимости, данный тезис носит характер суждения об этом понятии и его невозможно строго доказать или опровергнуть. Перед точным определением вычислимой функции математики часто использовали неофициальный термин, «эффективно вычислимый» для описания функций, которые можно вычислить с помощью бумажно-карандашных методов.

В терминах вычислимости по Тьюрингу тезис гласит, что для любой алгоритмически вычислимой функции существует вычисляющая её значения машина Тьюринга:
Позднее были сформулированы другие практические варианты утверждения:

физический тезис Чёрча — Тьюринга: любая функция, которая может быть вычислена физическим устройством, может быть вычислена машиной Тьюринга;
сильный тезис Чёрча — Тьюринга: любой конечный физический процесс, не использующий аппарат, связанный с непрерывностью и бесконечностью, может быть вычислен физическим устройством.

Способы записи алгоритмов.#

В настоящее время существуем много языков для записи алгоритмов, они называются алгоритмическими. Алгоритмический язык – это совокупность символов и правил их написания, используемых для записи алгоритмов. Выбор языка в каждом конкретном случае зависит от двух факторов:
1. На какого исполнителя – человека или автоматическое устройство рассчитан алгоритм;
2. Какие команды входят в систему команд исполнителя (СКИ).
Для записи алгоритмов, рассчитанных на исполнение автоматическими устройствами, нужна полная формализация, для этого используют специальные алгоритмические языки (Паскаль, СИ, Бейсик).
Рассмотрим способы записи алгоритма, рассчитанные на исполнителя - человека. Такие записи не полностью формализованы, так как для людей важны понятность и наглядность, поэтому для записи таких алгоритмов используют естественный или графический язык.

На практике наиболее распространены следующие формы представления алгоритмов:
- словесная (запись на естественном языке)
- графическая (изображения из графических символов)
- псевдокоды (полуформализованные описания алгоритмов на условном алгоритмическом языке, включающие в себя как элементы языка программирования, так и фразы естественного языка, общепринятые математические обозначения и др.
- программная (тексты на языках программирования)

Словесный способ записи алгоритма#

Словесный способ записи алгоритмов представляет собой описание последовательных этапов обработки данных. Алгоритм задается в произвольном изложении на естественном языке.

Алгоритм ПОГОДА  
Начало  
определить температуру воздуха  
если температура ниже 0, то надеть шубу, иначе надеть куртку  
Конец.

Словесный способ не имеет широкого распространения, так как такие описания:
- строго не формализуемы;
- страдают многословностью записей;
- допускают неоднозначность толкования отдельных предписаний.

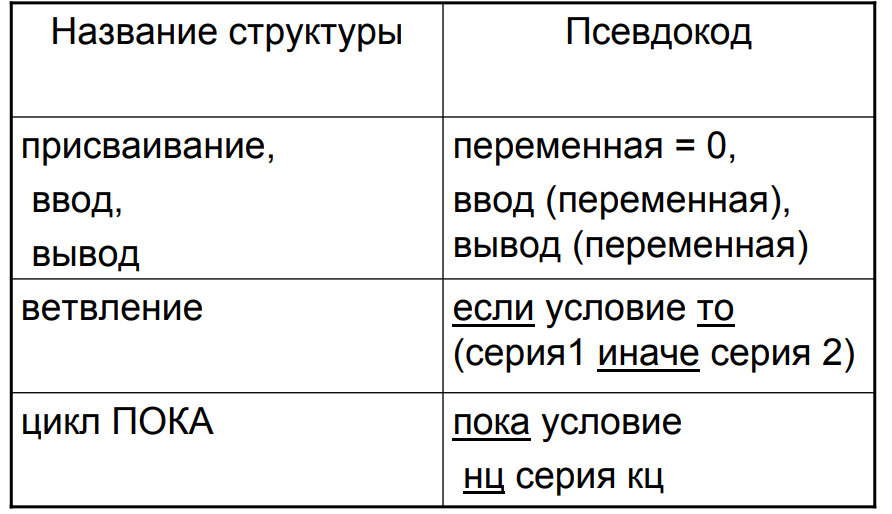
Псевдокод.#

Псевдокод представляет собой систему обозначений и правил, предназначенную для единообразной записи алгоритмов.

Псевдокод занимает промежуточное место между естественным и формальным языками. С одной стороны, он близок к обычному естественному языку, поэтому алгоритмы могут на нем записываться и читаться как обычный текст. С другой стороны, в псевдокоде используются некоторые формальные конструкции и математическая символика, что приближает запись алгоритма к общепринятой математической записи.

В псевдокоде не приняты строгие синтаксические правила для записи команд, присущие формальным языкам, что облегчает запись алгоритма на стадии его проектирования и дает возможность использовать более широкий набор команд, рассчитанный на абстрактного исполнителя.

Однако в псевдокоде обычно имеются некоторые конструкции, присущие формальным языкам, что облегчает переход от записи на псевдокоде к записи алгоритма на формальном языке. В частности, в псевдокоде, так же, как и в формальных языках, есть служебные слова, смысл которых определен раз и навсегда. Они выделяются в печатном тексте жирным шрифтом, а в рукописном тексте подчеркиваются.

Единого или формального определения псевдокода не существует, поэтому возможны различные псевдокоды, отличающиеся набором служебных слов и основных (базовых) конструкций.

Блок-Схемы#

Наибольшее распространение благодаря своей наглядности получил графический способ записи алгоритмов. При графическом представлении алгоритм изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий.

Такое графическое представление называется схемой алгоритма или блок-схемой. В блок-схеме каждому типу действий (вводу исходных данных, вычислению значений выражений, проверке условий, управлению повторением действий, окончанию обработки и т.п.) соответствует геометрическая фигура, представленная в виде блочного символа. Блочные символы соединяются линиями переходов, определяющими очередность выполнения действий.

Язык блок-схем прост (хотя существуют его расширенные варианты):

Прямоугольник – выполнение действия (например, c = a + b)
Ромб – проверка условия (например, a > b). Если условие выполняется, то алгоритм идет по линии «да», если не выполняется – то по линии «нет».
Скругленный прямоугольник – начало и конец алгоритма
Скошенный прямоугольник – ввод-вывод данных (например, получение значения переменной, вывод результата на экран монитора).

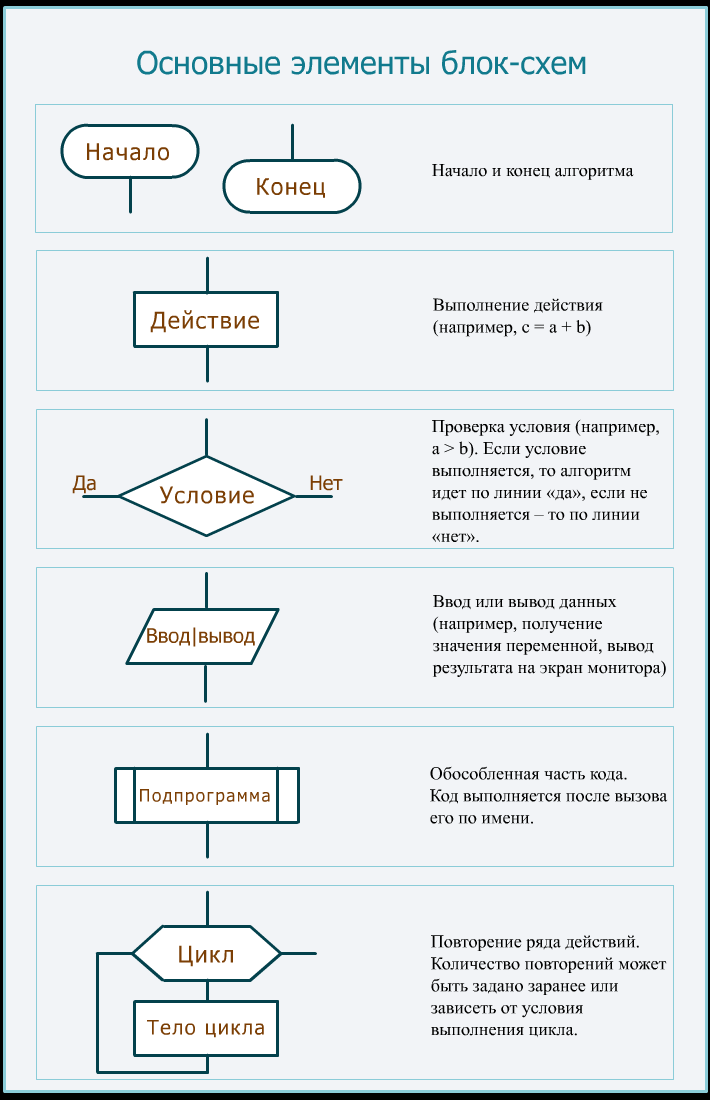
Основополагающим документами могут служить ГОСТ 19.701-90 Единая система программной документации. Схемы алгоритмов, программ, данных и систем. Условные обозначения и правила выполнения и Стандарты связанные с языком UML

В таблице приведены наиболее часто дополнительно употребляемые символы.

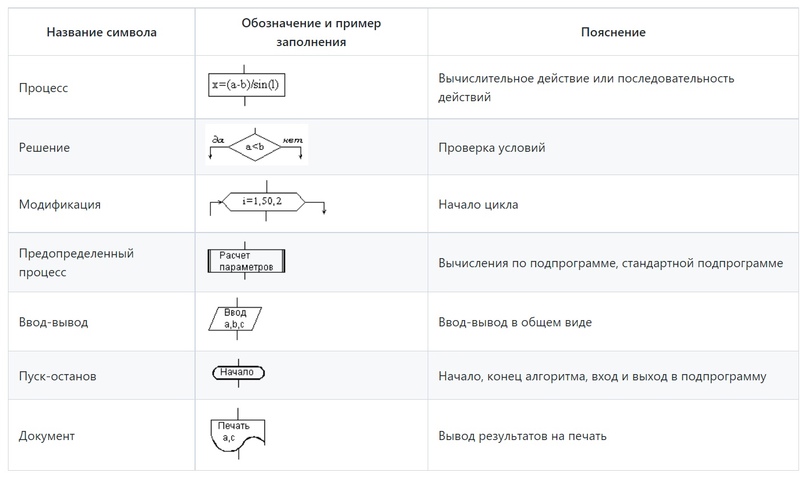
Блок процесс применяется для обозначения действия или последовательности действий,изменяющих значение, форму представления или размещения данных. Для улучшения наглядности схемы несколько отдельных блоков обработки можно объединять в один блок. Представление отдельных операций достаточно свободно.

Блок решение используется для обозначения переходов управления по условию. В каждом блоке решение должны быть указаны вопрос, условие или сравнение, которые он определяет.

Блок модификация используется для организации циклических конструкций. (Слово модификация означает видоизменение, преобразование). Внутри блока записывается параметр цикла, для которого указываются его начальное значение, граничное условие и шаг изменения значения параметра для каждого повторения.

Блок предопределенный процесс используется для указания обращений к вспомогательным алгоритмам, существующим автономно в виде некоторых самостоятельных модулей, и для обращений к библиотечным подпрограммам.

Блок Ввод-вывод используется для преобразования данных в форму, пригодную для обработки (ввод) или отображения результатов обработки (вывод). Отдельным логическим устройствам компьютера или отдельным функциям обмена соответствуют определенные блочные символы. В каждом из них указываются тип устройства или файла данных, тип информации, участвующий в обмене, а также вид операции обмена.

Блок Начало-конец используется для обозначения начала, конца, прерывания процесса обработки данных или выполнения программы.

Блок Документ предназначен для ввода-вывода данных, носителем которых служит бумага.

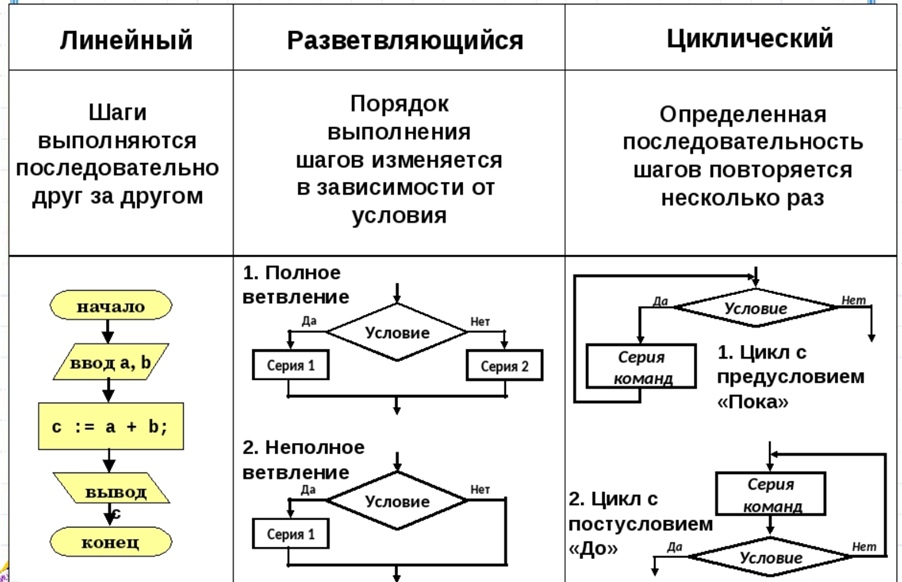
Виды Алгоритмов#

Различают три основных вида алгоритмов:

линейный алгоритм,
разветвляющийся алгоритм,
циклический алгоритм.

Линейный алгоритм – это алгоритм, в котором действия выполняются однократно и строго последовательно.

Самый простой пример реализации линейного алгоритма – путь из университета домой.

Словесный способ записи данного алгоритма:

выйти из университета на остановку;
подождать нужный автобус;
сесть на нужный автобус;
оплатить проезд;
выйти на требуемой остановке;
дойти до дома.
Очевидно, что данный пример относится к линейному алгоритму, т.к. все действия следуют одно за другим, без условий и повторений.

Разветвляющийся алгоритм – это алгоритм, в котором в зависимости от условия выполняется либо одна, либо другая последовательность действий.

Самый простой пример реализации разветвляющегося алгоритма – если на улице идет дождь, то необходимо взять зонт, иначе не брать зонт с собой.

Приведенный выше пример псевдокода по нахождению частного двух чисел также относится к разветвляющемуся алгоритму.

Циклический алгоритм – это алгоритм, команды которого повторяются некое количество раз подряд.

Самый простой пример реализации циклического алгоритма – при чтении книги будут повторяться одни и те же действия: прочитать страницу, перелистнуть и т.д.

Примеры известных алгоритмов#

Алгоритм Евклида – это алгоритм нахождения наибольшего общего делителя (НОД) пары целых чисел.
Наибольший общий делитель (НОД) – это число, которое делит без остатка два числа и делится само без остатка на любой другой делитель данных двух чисел. Проще говоря, это самое большое число, на которое можно без остатка разделить два числа, для которых ищется НОД.

Описание алгоритма нахождения НОД делением
1. Большее число делим на меньшее.
2. Если делится без остатка, то меньшее число и есть НОД (следует выйти из цикла).
3. Если есть остаток, то большее число заменяем на остаток от деления.
4. Переходим к пункту 1.

700
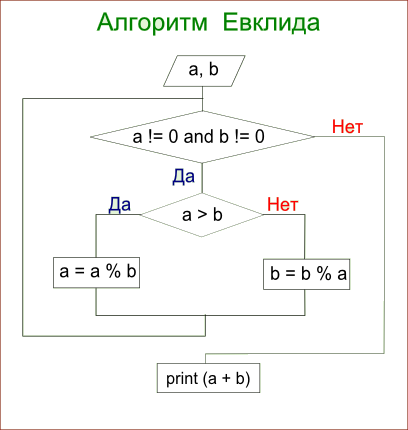
Пример:
Найти НОД для 30 и 18.
30/18 = 1 (остаток 12)
18/12 = 1 (остаток 6)
12/6 = 2 (остаток 0). Конец: НОД – это делитель. НОД (30, 18) = 6

Используемая литература#

Алгоритмы. Учебное пособие – М.: Мир науки, 2019. – Сетевое издание. Режим доступа: https://izd-mn.com/PDF/33MNNPU19.pdf – Загл. с экрана.
Пильщиков В.Н., Абрамов В.Г., Вылиток А.А., Горячая И.В. Машина Тьюринга и алгоритмы Маркова. Решение задач. (Учебно-методическое пособие) - М.: МГУ, 2006. – 47 с
Алгоритмы вычисления частичных функций : учебно-методическое пособие / Е.Л. Ефремов. – Владивосток : Издательство Дальневосточного федерального университета, 2021. – 48 с. ISBN 978-5-7444-5020-5.

Ссылка на материалы по практике#

Машина Тьюринга для системы Windows
Машина Тьринга Web-версия