Системы координат, пространственные операторы и векторные данные#

С чего начинаются координаты#

Тема пространственных систем координат — одна из самых непростых в ГИС. В повседневной жизни этот термин часто используют неправильно, а сама тема кажется скучной — вроде бухгалтерии в Диснейленде. Однако именно она обеспечивает корректную работу всех "аттракционов" геоинформационной системы.

Попробуйте наложить две бумажные карты одного и того же места. Даже если точки совпадут, остальная часть карт, скорее всего, нет — ведь они могут быть построены в разных системах координат. Пять сантиметров на одной карте могут означать соседнюю улицу, а на другой — другой континент.

Чтобы объединять данные из разных источников, специалист по ГИС должен понимать, как устроены пространственные системы координат. Существует несколько стандартов, самый известный из них — EPSG (European Petroleum Survey Group). Если два набора данных имеют одинаковый номер EPSG, они точно совпадут.

Но старые данные часто не содержат EPSG-кодов, поэтому приходится разбираться в структуре системы: эллипсоид, датум и проекция.

Геоид#

Note

Геоид — это эквипотенциальная поверхность земного поля тяжести (уровенная поверхность), приблизительно совпадающая со средним уровнем вод Мирового океана в невозмущённом состоянии и условно продолженная под материками.

Если смотреть на Землю с орбиты, она кажется ровным и блестящим голубым шаром. Но стоит опуститься на поверхность — и перед глазами открываются горы, долины, разломы и впадины океанов, уходящие на километры вглубь. Поверхность планеты далеко не гладкая — она скорее напоминает подгоревший пирог, чем идеальный шар. Даже привычное представление о сферической форме Земли неточно: планета немного сплюснута у полюсов. Если двигаться вдоль экватора, путь окажется длиннее примерно на 43 километра, чем при путешествии по меридиану.

Как же точно определить положение точки на столь неровной и асимметричной поверхности? Современные спутниковые навигаторы позволяют получить координаты любого участка Земли, представляя его в виде трёхмерной координаты. Подобные принципы лежат в основе цифровых моделей рельефа. В теории можно даже выбрать в качестве точки отсчёта не Землю, а, например, Луну или спутник, чтобы избавиться от зависимости от нестабильной земной поверхности.

Однако для повседневных задач такая точность избыточна. Нам нужна модель, которая будет достаточно точной, но при этом не потребует чрезмерных вычислений. Возможность вычислить координаты до двадцатого знака после запятой вовсе не означает, что это оправдано. Модель — это всегда упрощённое описание реальности. Она не обязана быть идеальной, главное — чтобы подходила под конкретную задачу.

Например, туристическая карта Москвы отлично подойдёт гостю города, но будет бесполезна для пилота вертолёта, пролетающего над МКАДом. Так и в геодезии: разные модели служат разным целям.

Первый вопрос, который возникает при создании геодезической модели, — как определить саму поверхность Земли. Использовать ли средний уровень моря? Или сгладить все горы и низины? А может, учитывать глубину океанов или границы тектонических плит? Универсального решения нет, потому что ни один стандарт не подходит одинаково для всех регионов планеты.

Даже понятие уровня моря неоднозначно. Допустим, житель Санкт-Петербурга измеряет высоту своего дома — 40 метров над уровнем моря. В то же время человек во Владивостоке получает аналогичное значение. Можно ли сказать, что оба дома находятся на одной высоте? Нет, потому что уровень моря отличается в зависимости от региона и не совпадает с фиксированным расстоянием до центра Земли.

Да и само понятие центра Земли не столь однозначно. Ещё в начале XIX века Карл Фридрих Гаусс, исследуя силу тяжести, предложил интересный метод описания формы планеты. Он измерял гравитацию с помощью маятника и выделял поверхность, где эта сила одинакова. Так появилась идея геоида — фигуры, отражающей реальное распределение масс в земных недрах.

На практике геоид значительно отличается от идеальной сферы. Из-за неоднородности внутреннего строения Земли масса распределена неравномерно, и на поверхности образуются участки повышенной и пониженной гравитации — своеобразные «выпуклости» и «провалы». Это делает Землю ещё менее похожей на идеальный шар и даже на приплюснутый апельсин.

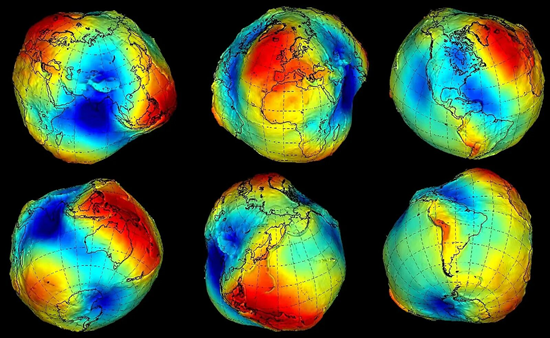
Хотя термин геоид редко встречается в практических задачах ГИС, именно он служит фундаментом для геодезических и планарных моделей. В географическом моделировании чаще используют эллипсоиды — упрощённые варианты геоида, которые дают достаточно точное приближение для большинства вычислений и картографических задач.

Эллипсоиды#

Первые представления о модели Земли в виде эллипсоида возникли ещё у древнегреческих мыслителей.
С математической точки зрения, эллипсоид — это объёмный эллипс, имеющий три полуоси: две экваториальные (a и b) и одну полярную (c).
Если все три полуоси равны (a = b = c), получается сфера.
Когда a = b, но c меньше, говорят о сплюснутом сфероиде.
Земля по своей форме ближе именно к такому сфероиду, напоминая слегка приплюснутый мандарин.

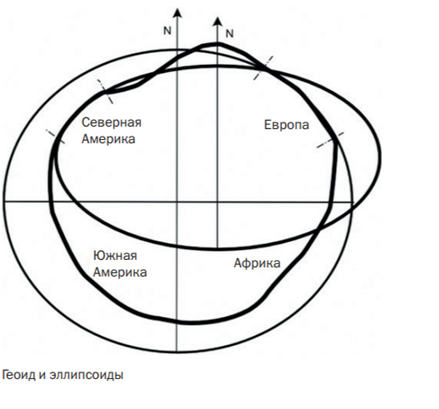
Меняя длины экваториальной и полярной полуосей, можно изменять степень сжатия эллипсоида.
Когда-то в геодезии предполагали, что достаточно использовать один универсальный опорный эллипсоид (или референц-эллипсоид) для всей планеты, полагая, что он будет одинаково точен в любой точке Земли.
Однако эта идея оказалась несостоятельной.
Измерения показали, что геоид — реальная форма Земли — имеет различную кривизну в зависимости от региона.
Эллипсоид, точно описывающий поверхность в одном месте, может давать большие ошибки в другом.
Поэтому в разных странах начали создавать локальные эллипсоиды, более точно отражающие геометрию Земли в конкретных областях.
Многие из таких моделей используются и сегодня.

Пока учёные и инженеры разных стран работали изолированно, различия между эллипсоидами не мешали.
Но с развитием авиации, навигации и особенно добычи нефти, когда требовалась точная международная координация, множество разных моделей стало вызывать путаницу.
С переходом от парусных кораблей к самолётам и спутникам возникла необходимость в единой глобальной системе.
Так появились два основных эллипсоида: World Geodetic System (WGS 84) и Geodetic Reference System (GRS 80).
На практике чаще применяется WGS 84, лежащий в основе GPS-навигации.

Примечание:
Цифры 80 и 84 в названиях GRS 80 и WGS 84 указывают на годы утверждения стандартов — 1980 и 1984 соответственно.
Различия между ними несущественны.

Следует помнить, что WGS 84 — не просто эллипсоид.
Эта система также включает модель геоида, известную как EGM96 (Gravitational Model of the Earth 1996).
Иными словами, WGS 84 сочетает эллипсоид с геоидом, обеспечивая наилучшее соответствие реальной гравитационной поверхности Земли для выбранных геодезических пунктов.
Со временем использовались разные эллипсоиды, некоторые из которых всё ещё актуальны, особенно для региональных задач.
Исторические данные часто привязаны именно к тем моделям, которые применялись на момент их сбора.

Эллипсоид	Экваториальная полуось (м)	Полярная полуось (м)	Обратное сжатие	Регион применения
Кларка 1866	6 378 206,4	6 356 583,8	294,9786982	Северная Америка
NAD 27	6 378 206,4	6 356 583,8	294,9786982	Северная Америка
Австралийский 1966	6 378 160	6 356 774,719	298,25	Австралия
GRS 80	6 378 137	6 356 752,3141	298,257222101	Северная Америка
WGS 84	6 378 137	6 356 752,3142	298,257223563	Весь мир (GPS)
IERS 1989	6 378 136	6 356 751,302	298,257	Время (глобально)

Старейшим и наиболее известным считается эллипсоид Кларка 1866, почти идентичный NAD 27,
поэтому они взаимозаменяемы в большинстве практических случаев.

Датум и его функции#

Чтобы связать математическую поверхность эллипсоида с реальной поверхностью Земли, вводится понятие датума. Датум — это совокупность параметров, определяющих положение и ориентацию эллипсоида относительно центра масс Земли. Он задаётся тремя координатными сдвигами (ΔX, ΔY, ΔZ), углами поворота (rX, rY, rZ) и масштабным коэффициентом, который регулирует размеры модели относительно реальной планеты.

Различают два типа датума: геоцентрический и локальный. В геоцентрических системах, например WGS 84, начало координат совпадает с центром масс Земли. В локальных датум подстраивается под конкретную территорию, обеспечивая высокую точность в пределах ограниченной области, но теряя её за пределами региона.

Чтобы использовать эллипсоид в навигационных системах, необходимо зафиксировать его относительно конкретного места на Земле. Так как эллипсоид не является идеальной сферой, у него существуют два полюса — точки пересечения оси вращения с поверхностью. Эти полюса должны быть связаны с реальными точками на планете, и такую привязку обеспечивает датум (или система отсчёта). Даже если два набора координат используют один и тот же эллипсоид, их точки привязки могут различаться.

Для наглядности можно привести пример с различием между географическими и магнитными полюсами. Обе модели описывают Землю одинаково по форме, но первая опирается на географический Северный полюс, а вторая — на магнитный, который смещён и располагается в пределах северной Канады.

Для точного соответствия модели и поверхности применяются два типа датумов:
- горизонтальный датум, определяющий точку Земли, относительно которой «привязан» эллипсоид;
- вертикальный датум, задающий значение высоты относительно принятой нулевой поверхности (например, уровня моря).

Примером может служить Североамериканский датум 1927 года (NAD 27), привязанный к ранчо Мидс в Канзасе, так как оно находится недалеко от географического центра США. В данном случае NAD 27 выступает и как горизонтальный, и как вертикальный датум.

Некоторые известные и широко применяемые датумы:
- NAD 83 — Североамериканский датум 1983 года, обычно используется с эллипсоидом GRS 80;
- NAD 27 — Североамериканский датум 1927 года, основанный на эллипсоиде Кларка 1866;
- Европейский датум 1950 года — используется на территории Европы;
- Австралийская геодезическая система 1984 года — применяется в Австралии и Океании.

Note

Постановлением Правительства РФ № 1240 от 24 ноября 2016 устанавливается период обновления датумов для «Параметров Земли» ПЗ-90 — раз в 10 лет.

Построение пространственных систем координат#

Часто пространственную систему координат, применяемую в ГИС, ошибочно отождествляют с геометрической системой координат. На деле геометрическая система — лишь один из элементов, необходимых для описания пространственной системы координат. Её основная задача — задать положение точки на референц-эллипсоиде.

Обычно для эллипсоида используется географическая система координат (или геодезическая система координат), обозначаемая как lon/lat. Она основана на двух угловых величинах: долготе и широте.
Линии, проходящие от одного полюса к другому, формируют меридианы и определяют долготу,
а линии, параллельные экватору, задают широту.

Хотя такие системы координат чаще всего применяются для описания всей Земли, их можно использовать и для любого референц-эллипсоида. Более того, принцип остаётся тем же для любого объекта, напоминающего эллипсоид — например, для арбуза, где продольные полосы можно представить как меридианы.

Основы пространственных систем координат#

Подводя итог обсуждения пространственных систем координат, можно выделить несколько ключевых этапов их построения:

Сначала формируется модель Земли в виде подходящего референц-эллипсоида — такой поверхности, которая наилучшим образом соответствует форме геоида в пределах рассматриваемой территории.
Затем с помощью датума выполняется привязка этого эллипсоида к конкретному положению в пространстве, а для указания точек на его поверхности вводится система координат.

Например, нулевая миля в Вашингтоне (округ Колумбия) имеет координаты W −77,03655, N 38,8951 при использовании эллипсоида и датума WGS 84. Если же задать те же координаты в системе NAD 27 с эллипсоидом Кларка 1866, значения немного изменятся — W −77,03685, N 38,8950.

Таким образом, мы располагаем всеми элементами, необходимыми для точного указания любой точки на Земле. Более того, можно разрабатывать алгоритмы для преобразования координат между различными эллипсоидами и датумами.

Во многих наборах географических данных координаты не проецируются на плоскую поверхность и хранятся в виде широты и долготы. Такие данные называют неспроецированными.
Они позволяют решать множество задач — например, вычислять расстояние по дуге большого круга между двумя точками или строить маршруты перемещения по поверхности Земли.

Местные системы координат (МСК)#

Местные системы координат (МСК) применяются в России для инженерных и кадастровых работ. Они регламентированы положениями, содержащими параметры перехода из общеземных систем (WGS84, ПЗ-90) в локальные. В этих положениях указываются сдвиги по осям, углы вращения, масштабный коэффициент, а также параметры эллипсоида, чаще всего эллипсоида Красовского.

В положениях о МСК обычно приводятся все сведения, необходимые для корректного перехода между различными системами координат. Такие переходы осуществляются на основе алгоритмов, описанных в ГОСТ Р 51794–2001 «Системы координат», и выполняются в двух основных направлениях:
- из глобальной системы координат WGS-84 (ПЗ-90) в МСК и обратно;
- из общегосударственной системы координат СК-95 в МСК и обратно.

Документ указывает номенклатурные номера листов топографических карт масштаба 1:100 000, на основе которых создаётся местная система координат.
Эти карты служат базовой основой для всех геодезических и картографических работ в пределах охваченной территории. Кроме того, в положении обозначается общая площадь и границы региона, в пределах которого действуют параметры данной МСК.

Ключевым элементом любой МСК являются параметры преобразований, обеспечивающие связь между государственной геоцентрической системой координат (ПЗ-90) и локальной системой.
Они определяют, как глобальная модель Земли совмещается с региональной моделью и включают семь значений:

Сдвиги по осям X, Y, Z (Δx, Δy, Δz) — описывают линейное смещение начала координат локальной системы относительно центра геоцентрической системы.
Углы вращения (Wx, Wy, Wz) — отражают ориентацию осей МСК относительно осей глобальной системы.
Масштабный коэффициент (m) — характеризует разницу масштабов между двумя системами.

Для более точного регионального выравнивания дополнительно задаются семь аналогичных параметров перехода между СК-95 (государственная система координат) и конкретной МСК.
Таким образом обеспечивается согласованность между федеральными и местными геодезическими данными, что особенно важно при проектировании инженерных сетей, кадастровых измерениях и геодезическом контроле.

Элипсоид в МСК#

В качестве математической основы МСК используется эллипсоид Красовского, на котором строится вся координатная сеть региона.
Его параметры:
- Большая полуось (a) = 6 378 245 м
- Сжатие (1/f) = 298,3

Эллипсоид Красовского был разработан специально для территории бывшего СССР и наилучшим образом аппроксимирует форму геоида в пределах Евразии.

Форматы описания систем координат#

Современные геоинформационные системы поддерживают несколько стандартных форматов для описания систем координат. Каждый из них предназначен для разных сценариев обмена и хранения данных:

Well-Known Text (WKT) — текстовый формат, подробно описывающий параметры проекции, датума и эллипсоида.
Используется в большинстве ГИС-пакетов (ArcGIS, QGIS) и хранится, например, в файлах .prj.
PROJ string — компактная строковая форма описания, применяемая библиотекой PROJ.
Пример:
+proj=tmerc +lat_0=0 +lon_0=9 +k=1 +x_0=500000 +y_0=0 +ellps=GRS80 +units=m +no_defs
Коды EPSG / ESRI / IAU / SpatialReference.org — числовые идентификаторы систем координат.
Например, EPSG:4326 соответствует системе WGS-84.

Файлы формата .prj содержат описание проекции в виде структуры WKT, включающей сведения о проекции, датумах, единицах измерения и смещениях.
Ниже приведён пример:

Пример записи проекции в формате .prj:

PROJCS["Projection_name",
 GEOGCS["GeographicCS",
 DATUM["Datum_name",
 SPHEROID["Krassowsky 1940",6378245,298.3],
 TOWGS84[0,0,0,0,0,0,0]],
 PRIMEM["Greenwich",0],
 UNIT["degree",0.01745329251994328]],
 PROJECTION["Transverse_Mercator"],
 PARAMETER["central_meridian",36],
 UNIT["metre",1]]

Эта структура читается большинством программ ГИС и используется для точного восстановления параметров системы координат при открытии картографических файлов.

Пример описания МСК — Москва#

Полный перечень местных систем координат можно найти на официальном сайте Росреестра:
https://rosreestr.gov.ru/activity/geodeziya-i-kartografiya/mestnye-sistemy-koordinat/

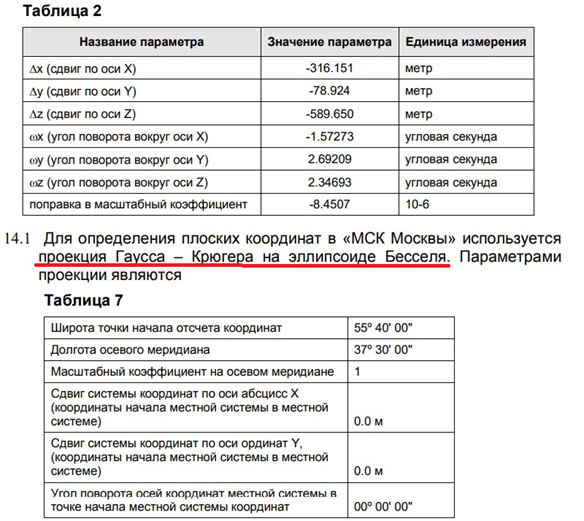
Для Москвы параметры МСК заданы следующим образом:

Широта начала отсчёта координат:
55° 40′ 00″ → +lat_0 = 55.666667
(пересчёт: 55 + 40 / 60 = 55.66667)
Долгота осевого меридиана:
37° 30′ 00″ → +lon_0 = 37.5
Масштабный коэффициент:
+k = 1

Warning

Обратите внимание, что мы меняем знаки перед вводом в систему!

Эллипсоид и параметры перехода:
+ellps = bessel
+towgs84 = 316.151,78.924,589.650,-1.57273,2.69209,2.34693,8.4507
Единицы измерения:
+units = m

Итоговая строка описания в формате PROJ

+proj=tmerc +lat_0=55.66666666667 +lon_0=37.5 +k=1 +x_0=16.098 +y_0=14.512 +ellps=bessel +towgs84=316.151,78.924,589.650,-1.57273,2.69209,2.34693,8.4507 +units=m +no_defs

Параметры x_0 и y_0 могут корректироваться вручную для точного совмещения с конкретным участком местности.
Однако при этом в соседних областях возможны небольшие невязки координат.
Пример: x_0 = 16.098, y_0 = 14.512.

Проекции#

Если мысленно распрямить земной эллипсоид и положить его на плоскость, получится его плоское отображение, или картографическая проекция. Любая подобная операция неизбежно связана с искажениями, ведь трёхмерную поверхность эллипсоида невозможно перенести на двумерную плоскость без потерь. Тем не менее, двумерные карты получили повсеместное распространение — не только потому, что глобус неудобно использовать, но и благодаря математической простоте евклидовой геометрии, на которой основаны вычисления в большинстве программ и библиотек, включая PostGIS.

В отличие от эллипсоида, декартова плоскость позволяет работать с простыми геометрическими соотношениями. Здесь площадь квадрата равна квадрату его стороны, а расстояние между точками вычисляется по теореме Пифагора. Такая модель идеально подходит для печатных карт, чертежей и цифровых представлений на экране. На поверхности эллипсоида те же вычисления становятся значительно сложнее: даже определение понятия «квадрат» требует уточнения.

С развитием PostGIS появилась возможность строить модели не только для Земли, но и для других планет. Начиная с версии 2.3, тип данных geography поддерживает любые сфероиды, что позволяет описывать поверхности других небесных тел. Хотя библиотека изначально ориентирована на земные координаты, она способна работать с любыми зарегистрированными системами координат, даже не привязанными к Земле.

То, как именно происходит преобразование эллипсоида в плоскую поверхность, зависит от задачи. Различные классы картографических проекций стремятся оптимизировать определённые свойства пространства. Каждая система координат ограничена определённой территорией и использует свои единицы измерения (обычно метры или футы). При создании проекции приходится искать компромисс между четырьмя характеристиками:

точностью измерения расстояний,
сохранением формы (корректностью углов),
направлением (ориентацией по сторонам света),
площадью охвата.

Попытка охватить большую территорию обычно приводит к потере точности либо требует работы с несколькими системами координат. Чем шире охват, тем сильнее искажения. Если сохранить форму объектов, то расстояния начинают «плыть»; если стремиться к точным измерениям — теряется правильная форма.

Существует множество разновидностей проекций, каждая из которых ориентирована на собственную цель. Наиболее известные из них:

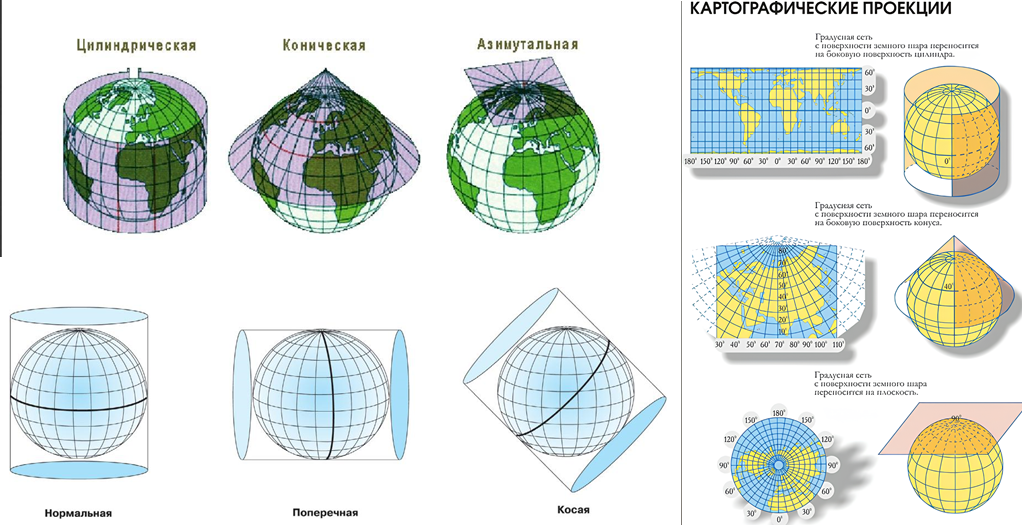
Цилиндрические проекции — поверхность Земли как будто «разворачивается» с цилиндра, обёрнутого вокруг неё. Самая известная из них — проекция Меркатора, где цилиндр касается экватора. Вблизи полюсов она даёт серьёзные искажения, зато около экватора передаёт расстояния точнее.
Конические проекции — Землю мысленно оборачивают конусом, после чего конус разворачивают на плоскость. Такие проекции лучше сохраняют форму на средних широтах.
Азимутальные проекции — проецируют поверхность на плоскость, касающуюся эллипсоида в одной точке; подходят для отображения полярных областей.

Каждая из этих проекций может быть ориентирована по-разному:
- наклонно — когда ось не параллельна и не перпендикулярна экватору,
- экваториально — если плоскость проекции перпендикулярна экватору,
- поперечно — когда цилиндр или конус направлен вдоль экватора.

Комбинации этих типов формируют основные классы декартовых систем координат:

Равновеликие азимутальные проекции Ламберта (LAEA) — хорошо подходят для измерения площадей и расстояний на больших территориях, но заметно искажают форму объектов. Для США используется система US National Atlas (EPSG:2163), основанная на метрах.
Равноугольные конические проекции Ламберта (LCC) — обеспечивают сохранение формы и направлений, но искажают площадь. Идеальны для средних широт, вытянутых с запада на восток. Применяются в авиационных картах, национальных системах координат и государственных картах США.
Универсальные поперечные проекции Меркатора (UTM) — достаточно точно сохраняют расстояния, форму и направления, однако каждая зона охватывает лишь 6° по долготе, поэтому для всего земного шара нужно 60 отдельных зон. Для полюсов они не подходят.
Проекции Меркатора (в глобальном масштабе) — прекрасно сохраняют углы и направления, но сильно искажают размеры областей, особенно в высоких широтах. Среди них наиболее известны:
World Mercator (SRID:3395),
Spherical Mercator (Google Mercator, SRID:3857) — современный стандарт EPSG, используемый в веб-картах.
Эти системы удобны тем, что опираются на единую систему координат и воспринимаются пользователями интуитивно.
Национальные системы координат — варианты UTM или LAEA, адаптированные для конкретных стран. Например, US National Atlas Equal Area (SRID:2163) охватывает всю территорию США.
Системы координат штатов — узкие региональные варианты, обычно производные от UTM. Они обеспечивают высокую точность измерений и используются в геодезии, но применимы лишь в пределах одного штата.
Географическая проекция — система WGS 84 (EPSG:4326) может храниться в типе geometry, но для корректной обработки данных чаще используется тип geography, либо преобразуется в одну из плоских систем. При работе с geometry PostGIS просто воспринимает долготу как X, а широту как Y, выполняя внутреннее проецирование, известное как Plate Carrée (псевдопроекция).

Среди всего этого разнообразия не всегда легко определить, в какой системе координат заданы исходные данные, и какая проекция наиболее подходит для их обработки и хранения. В последующих разделах рассматриваются принципы выбора пространственной системы координат и упражнения, помогающие уверенно определять тип координатной привязки.

Tip

Современные версии **PostGIS** предоставляют возможность создавать **пространственные модели не только для Земли**, но и для **других планет и небесных тел**. Начиная с версии **2.3**, в систему был добавлен **тип данных geography**, основанный на **сфероидальной модели**, что обеспечивает поддержку **любой формы сфероида**. Это значит, что пользователь может описывать координаты и поверхности **Марса, Луны или других планет**, применяя тот же математический аппарат, что и для Земли.
Хотя архитектура PostGIS по умолчанию ориентирована на **земные системы координат**, её механизм пространственных преобразований способен работать **с любыми зарегистрированными системами координат (CRS)**, в том числе **внесолнечными или пользовательскими**. Таким образом, PostGIS можно рассматривать как **универсальную платформу пространственного моделирования**, пригодную не только для геоинформационных задач на Земле, но и для **планетологических и астрономических исследований**.

Выбор системы пространственной привязки для хранения данных#

Вопрос о том, какая пространственная система координат наиболее подходит для конкретного набора данных, встречается довольно часто. Однако однозначного ответа на него не существует — выбор зависит от масштаба проекта, характера анализируемых объектов, а также от того, какие метрики требуется сохранять точнее: расстояния, углы или форму.

В специализированных справочниках и документации PostGIS можно найти перечень наиболее распространённых систем координат с указанием их идентификаторов EPSG и SRID. В PostGIS идентификаторы, как правило, совпадают с кодами EPSG, но в других базах данных это соответствие не всегда соблюдается. Следует помнить, что одна и та же система координат может иметь разные числовые обозначения, в зависимости от того, каким источником определений пользуется конкретное программное обеспечение. Например, Esri применяет собственные обозначения SRID, которые часто эквивалентны EPSG, но лучше интегрированы в ArcGIS.

Ниже приведён обобщённый перечень наиболее употребительных пространственных систем координат и оценка их пригодности для решения различных задач:

EPSG/PostGIS SRID	Неформальное название	Охват	Измерения расстояний	Сохранение формы
4326	WGS 84 (долгота/широта)	Отлично	Плохо	Плохо
3785 / 900913 (старый номер)	Сферическая проекция Меркатора	Хорошо	Плохо	Хорошо
900913 (устаревший код)	Google Mercator	Хорошо	Плохо	Хорошо
32601–32760	UTM-зоны WGS 84	Средне	Хорошо	Хорошо
2163	Национальный атлас США (равновеликая проекция)	Хорошо	Средне	Средне
—	Системы координат штатов США	Средне	Хорошо	Хорошо

Примечание. Оценки в таблице являются относительными.
- Для критерия охват:
– «отлично» — покрытие всего земного шара;
– «хорошо» — охват крупных государств (например, США);
– «средне» — охват регионального масштаба (одного штата или нескольких градусов широты/долготы).
- Для измерений:
– «хорошо» означает точность в пределах метра для расчёта площадей и расстояний;
– «средне» — точность на уровне нескольких метров, при этом ошибка между удалёнными объектами может достигать десятков метров;
– «плохо» — искажения существенны, особенно в полярных областях, где площадь и расстояния значительно преувеличиваются.
- Последний столбец характеризует степень сохранения формы и углов при проецировании.

Если работа ведётся с региональными данными (например, в пределах одной страны или отдельного штата), то предпочтительно использовать национальные или государственные системы координат. Они обеспечивают достаточную точность при измерениях и корректное отображение объектов на карте, без значительных искажений.

Замечание. Любая декартова система координат, сохраняющая расстояния, применима только в ограниченной зоне. Если при использовании типа geometry необходимо обработать большие территории, то для поддержания точности придётся применять несколько пространственных систем координат, адаптированных к разным регионам, и выполнять их взаимное преобразование.

Когда нужно только отобразить карту#

Если задача состоит лишь в визуализации данных, а не в точных измерениях расстояний и площадей, то выбор проекции Меркатора может быть вполне оправдан. Несмотря на то, что базовые проекции Меркатора значительно искажают размеры объектов, особенно по мере удаления от экватора, они обладают важным преимуществом — картографические сервисы (например, Google Maps) используют их благодаря удобству отображения и единой системе координат, охватывающей весь земной шар.

Основные проекции#

Существует около тридцати основных картографический проекций и около двадцати систем координат. Если всё это перемножить, получится уйма разных вариаций для карт. Такое положение дел вводит в ступор неподготовленного пользователя, особенно в QGIS, когда выбираешь проекцию для работы с проектом. Так что же выбрать?

Проекция Web Mercator#

Web Mercator или WGS 84 / Pseudo Mercator — это стандарт веб-картографии. На основе этой проекции построены все веб-карты: 2GIS, Яндекс.Карты, OSM и прочие. Проекция работает в паре с системой координат WGS 84.

WGS 84 — всемирная геодезическая система Земли. Глобальная универсальная система координат, которая используется в морской, воздушной, наземной и космической навигации. За точку отсчёта здесь взят геометрический центр планеты.

Комбинацию WGS 84 / Pseudo Mercator также можно найти под названием EPSG:3857. Это её официальное название как картографического стандарта. Например, в QGIS проекция фигурирует именно под этим названием.

Проекция Web Mercator отлично подходит для визуализации глобальных данных, поскольку она изначально разработана для отображения всей планеты. Например, с помощью этой проекции можно визуализировать данные плотности населения Земли. Также её можно использовать для создания схем стран и регионов вблизи экватора, где искажения формы не такие сильные, как на полюсах.

Однако удобство визуализации достигается ценой точности:
- расстояния и площади в проекции Меркатора искажены, особенно вдали от экватора;
- при проведении пространственных вычислений (например, измерении расстояний между городами или площадей буферов) ошибки могут достигать десятков процентов.

Если проект требует метрической точности, следует подбирать проекцию, соответствующую региону интереса — например, UTM-зоны или локальные системы координат.

Проекция UTM zone X#

UTM, или универсальная поперечная проекция Меркатора, — универсальная проекция для работы с городами, регионами и небольшими странами. В отличие от других проекций, в UTM весь мир разбит на равные прямоугольники, и поэтому в ней нет сильных искажений форм и площадей.

Существует несколько типов проекций с разными системами координат. Например, ED50, которая используется только в Европе и частично охватывает Россию, или универсальная WGS 84, в которой есть все страны мира. Поэтому лучше использовать UTM в паре с WGS 84.

Для правильного применения проекции нужно знать номер и индекс зоны. С индексом всё просто: всё, что севернее экватора, имеет индекс N, всё, что южнее — индекс S.
С зоной посложнее: в UTM мир разбит на 60 зон с шагом в 6 градусов, зоны пронумерованы слева направо.
Для расчёта используется формула:

N = (L + 180) / 6,
где N — номер зоны, L — долгота объекта в градусах.

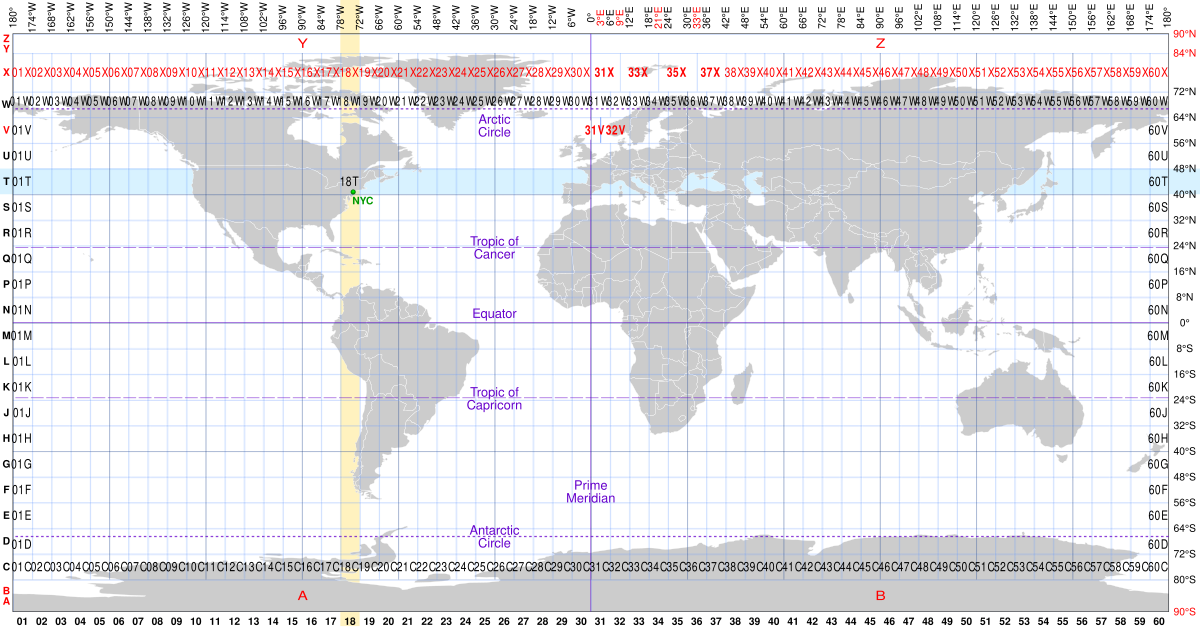
Так, Москва и Сочи находятся в зоне 37N, а Астана и Ханты-Мансийск — в зоне 42N. Чтобы не высчитывать нужную зону вручную, можно воспользоваться онлайн-сервисом: достаточно ввести название города, и вы получите номер и индекс зоны.

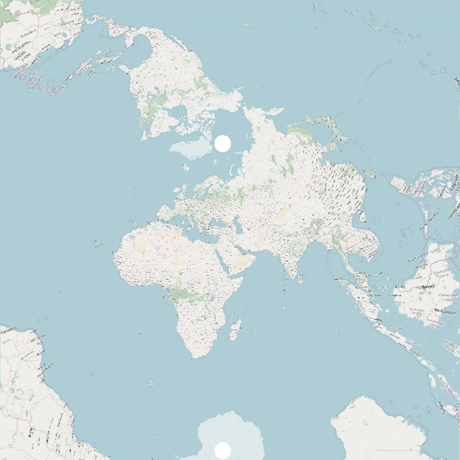
WGS 84 / UTM zone X подходит для небольших стран и регионов. Например, для Албании и Липецкой области проекция подойдёт идеально,
а вот для Грузии и Красноярского края — уже нет.
В целом, в проекции UTM лучше всего работать с картами и схемами городов или сопоставимых по масштабу территорий.

Проекция МСК-X зона X#

МСК (местные системы координат) — российский картографический стандарт, применяемый для всей геодезической и инженерной документации. Все проекты, проходящие государственную экспертизу, обязаны использовать именно эту систему координат. Она основана на модифицированной проекции Меркатора и по принципу построения похожа на UTM, но адаптирована под территориальное деление России.

Обычно для каждого региона существует отдельная МСК, однако есть исключения — например, в Красноярском крае действует три системы координат из-за большой площади региона. Номер МСК совпадает с номером субъекта федерации:
МСК-46 — Курская область, МСК-11 — Республика Коми и т. д.

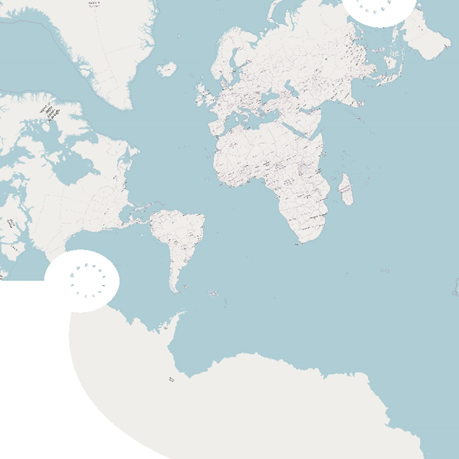
Система имеет свою специфику: внутри одного региона может быть несколько зон одной МСК с разными координатами. Чаще всего границы зон проходят по административным границам районов, но возможны исключения.

МСК не поддерживается большинством ГИС-программ напрямую, поэтому её приходится добавлять вручную, причём каждую зону отдельно.

Как добавить МСК в QGIS

Перейдите на сайт со списком МСК и найдите нужную зону.
В разделе «ГИС QGIS» скопируйте код нужной зоны.
В QGIS откройте меню пользовательских проекций:

• eng: Settings → Custom Projections → +
• рус: Установки → Пользовательские проекции → +

Введите название проекции.
В поле Format выберите Proj.
Вставьте скопированный код.
Нажмите Validate / Проверить, затем OK.

Теперь добавленную МСК можно выбирать как основную проекцию проекта или систему координат слоя.

Расчёт расстояний в разных системах координат#

Для иллюстрации различий можно рассчитать расстояния между аэропортами крупных городов, используя разные модели Земли и проекции.

WITH g1 AS (
    SELECT city, geog FROM ch03.city_airports
    WHERE city IN ('Beijing', 'Cairo', 'Sydney')
),
g2 AS (
    SELECT city, geog FROM ch03.city_airports
    WHERE city IN ('Melbourne', 'Philadelphia', 'São Paulo', 'Shanghai', 'Tel Aviv')
)
SELECT 
    g1.city AS city1, 
    g2.city AS city2,
    (ST_Distance(g1.geog, g2.geog, use_spheroid => false) / 1000)::integer AS sp,       -- ❶ Расстояние на сфере
    (ST_Distance(g1.geog, g2.geog, use_spheroid => true) / 1000)::integer AS spwgs84,  -- ❷ Расстояние на сфероиде
    (ST_Distance(
        ST_Transform(g1.geog::geometry, 3857),
        ST_Transform(g2.geog::geometry, 3857)
     ) / 1000)::integer AS wm                     -- ❸ Расстояние в Web Mercator
FROM g1 CROSS JOIN g2
WHERE g1.city <> g2.city
ORDER BY g1.city, g2.city;

❶ Расстояние, рассчитанное на сферической модели Земли.
❷ Расстояние, вычисленное с использованием сфероидальной модели.
❸ Расстояние, определённое в системе координат Web Mercator.

Таблица получена с помощью кода из листинга и демонстрирует значения расстояний между различными аэропортами, измеренных в трёх типах координатных систем: сферической WGS 84 (sp), сфероидальной WGS 84 (spwgs84) и Web Mercator (wm).
Во многих прикладных задачах, связанных с вычислением протяжённых расстояний, применяются именно сфероидальные или сферические расчёты. При этом вычисления на сфере дают менее точный результат, так как рассматривают Землю как идеальный шар, а не как эллипсоид. Сфероид WGS 84 обеспечивает максимально возможную точность при определении расстояний на больших протяжённостях.

Из анализа таблицы следует, что система Web Mercator значительно уступает по точности сфероидальной модели WGS 84.
Эта система координат плохо подходит для измерений, особенно когда речь идёт о точках, удалённых от экватора или расположенных на значительном расстоянии друг от друга.
Так, например, значение расстояния между Пекином и Филадельфией, вычисленное в проекции Меркатора, существенно расходится с реальной величиной.
Сферические вычисления, напротив, обеспечивают удовлетворительные результаты как для коротких, так и для протяжённых расстояний.

Таблица. Расстояния между городами (в километрах)

Первый город	Второй город	sp	spwgs84	wm
Пекин	Мельбурн	9113	9080	9923
Пекин	Филадельфия	11044	11070	21354
Пекин	Сан-Паулу	17576	17577	19664
Пекин	Шанхай	1100	1098	1357
Пекин	Тель-Авив	7141	7156	9162
Каир	Мельбурн	13942	13938	14977
Каир	Филадельфия	9167	9186	11946
Каир	Сан-Паулу	10218	10210	10661
Каир	Шанхай	8369	8385	10064
Каир	Тель-Авив	392	393	459
Сидней	Мельбурн	705	706	871
Сидней	Филадельфия	15883	15882	26720
Сидней	Сан-Паулу	13367	13386	22043
Сидней	Шанхай	7865	7837	8341
Сидней	Тель-Авив	14168	14166	15107

Как видно из таблицы, расхождения между результатами становятся особенно заметными в проекции Web Mercator, где искажения геометрии оказывают существенное влияние на вычисления.
Чтобы проверить, насколько эти искажения проявляются при вычислении площадей, можно выполнить код из следующего листинга, где рассматривается десятиметровая буферная зона, создаваемая в различных точках земного шара.

WITH g1 AS (
  SELECT city,
    ST_Area(
      ST_Buffer(
        ST_Transform(geog::geometry, upgis_utmzone_wgs84(geog::geometry)), 10
      )
    )::numeric(10,2) AS utm,  -- ❶ Буфер UTM.

    ST_Area(
      ST_Transform(
        ST_Buffer(
          ST_Transform(geog::geometry, upgis_utmzone_wgs84(geog::geometry)), 10
        ), 4326
      )::geography
    )::numeric(10,2) AS geog,  -- ❷ Буфер UTM на сфероиде.

    ST_Area(
      ST_Transform(
        ST_Buffer(
          ST_Transform(geog::geometry, upgis_utmzone_wgs84(geog::geometry)), 10
        ), 3857
      )
    )::numeric(10,2) AS wm  -- ❸ Буфер UTM в системе Web Mercator.

  FROM ch03.city_airports
  WHERE city IN ('Arlhangelsk', 'Bergen', 'Boston', 'Helsinki', 'Honolulu',
                 'Murmansk', 'Oslo', 'Paris', 'San Francisco', 'St. Peters')
)

SELECT g1.*, geog - utm AS diff_geog_utm, wm - utm AS diff_wm_utm
FROM g1
ORDER BY diff_wm_utm ASC;

❶ Буфер UTM.
❷ Буфер UTM на сфероиде.
❸ Буфер UTM в системе Web Mercator.

В таблице 3.4 показаны площади 10-метровых буферных зон, вычисленные по всему миру на основе листинга 3.2.
Буферы рассчитаны в трёх различных системах координат:

UTM (utm) — универсальная поперечная проекция Меркатора,
geography (geog) — на сфероиде WGS 84,
Web Mercator (wm) — проекция, применяемая во многих онлайн-картах.

В двух последних столбцах указаны различия между UTM и другими измерениями.
Буфер создаётся как круговой полигон радиусом 10 метров с центром в заданной точке в проекции UTM.
Затем он преобразуется в другую систему координат, где вычисляется площадь полученного многоугольника.

Таблица. Десятиметровые буферные зоны в разных регионах мира

Город	utm	geog	wm	diff_geog_utm	diff_wm_utm
Гонолулу	312.14	312.30	361.66	0.16	49.52
Сан-Франциско	312.14	312.37	498.74	0.23	186.60
Бостон	312.14	312.18	572.19	0.04	260.05
Париж	312.14	312.39	725.48	0.25	413.34
Санкт-Петербург	312.14	312.37	1229.85	0.07	917.71
Осло	312.14	312.21	1259.67	0.15	947.53
Берген	312.14	312.29	1267.28	0.14	955.14
Хельсинки	312.14	312.28	1269.19	0.16	957.05
Архангельск	312.14	312.30	1663.95	0.20	1351.81
Архангельск-1	312.14	312.34	1690.51	0.20	1378.37
Мурманск	312.14	312.39	2373.13	0.25	2060.99

Почему площадь 10-метрового буфера равна 312, а не 314 м²?#

Идеальный круг радиусом 10 м имеет площадь, равную
π × 10² ≈ 314 м².

Однако по умолчанию функция ST_Buffer в PostGIS создаёт многоугольник из 32 сторон,
где каждая четверть окружности аппроксимируется восемью точками.
Такое приближение даёт немного меньшую площадь — около 312 м².

Чтобы повысить точность, можно использовать перегруженную версию функции ST_Buffer,
позволяющую явно задать число сегментов, применяемых для аппроксимации четверти круга.

Пространственный анализ в PostGIS#

PostGIS — расширение к PostgreSQL, позволяющее выполнять геометрические и топологические операции с пространственными объектами. Основные инструменты включают операции буферизации, пересечения, объединения и анализ сетей.

Буферизация#

Буферизация создаёт область вокруг объекта на заданном расстоянии. Например, можно определить все здания в радиусе 500 м от реки.

SELECT ST_Buffer(geom, 500) FROM rivers;

Оверлейные операции#

Операции наложения позволяют создавать новые геометрии путём пересечения, объединения или исключения областей:
- ST_Intersection — вырезает пересекающуюся часть;
- ST_Union — объединяет геометрии;
- ST_SymDifference — возвращает области, принадлежащие только одной из фигур.

Пространственные запросы#

PostGIS поддерживает запросы по пространственным отношениям между объектами:

ST_Within(g1.geom, g2.geom)
ST_Intersects(g1.geom, g2.geom)
ST_DWithin(g1.geom, g2.geom, distance)

Эти функции позволяют, например, найти все здания внутри границ парка или определить все дороги, проходящие на расстоянии менее 100 м от водоёма.

Центроиды и геометрические медианы#

Для анализа распределения объектов используются функции ST_Centroid и ST_GeometricMedian. Первая возвращает центр геометрии, но не всегда располагается внутри неё, вторая же устойчива к выбросам и подходит для анализа групп точек.

Пример: определение центра активности пользователей в городе по геолокациям фотографий.

Анализ сетей: pgRouting#

Расширение pgRouting позволяет выполнять графовые задачи в пространственной среде. Оно работает поверх геометрий типа LINESTRING и используется для решения задач:

pgr_dijkstra — поиск кратчайшего пути;
pgr_ksp — несколько альтернативных маршрутов;
pgr_TSP — задача коммивояжера;
pgr_drivingDistance — определение зон доступности.

Растровый анализ#

PostGIS поддерживает и растровые операции. К числу ключевых относятся анализ близости и анализ видимости.

Анализ близости создаёт растр, в котором каждой ячейке присваивается значение ближайшего объекта. Применяется для построения зон влияния.
Анализ видимости (viewshed) определяет участки, видимые с заданной точки на основе цифровой модели рельефа.

Заключение#

Понимание систем координат и их параметров является необходимым условием корректного использования пространственных данных. От выбора проекции и датума зависит точность всех последующих вычислений — от измерения расстояний до анализа плотности населения. Инструменты PostGIS, QGIS и pgRouting позволяют не только выполнять пространственные преобразования, но и строить сложные модели взаимодействия объектов, анализировать доступность территорий, исследовать сезонную динамику активности или выявлять закономерности распределения явлений. Таким образом, грамотная работа с системами координат служит фундаментом для всех направлений пространственного анализа в современной геоинформатике.