Практика 14. Эвристические алгоритмы. Генетический алгоритм. Муравьиный алгоритм.#
Генетический алгоритм#
Генетический алгоритм (англ. genetic algorithm) — эвристический алгоритм поиска, используемый для решения задач оптимизации и моделирования путём случайного подбора, комбинирования и вариации искомых параметров с использованием механизмов, аналогичных естественному отбору в природе.
Существует множество теорий биологической эволюции (Ж.-Б. Ламарка, П. Тейяра де Шардена, К. Э. Бэра, Л. С. Берга, А. А. Любищева, С. В. Мейена и др.), однако ни одна из них не получила общепринятого статуса. Наиболее известной и широко обсуждаемой остаётся теория Чарльза Дарвина, изложенная в его труде «Происхождение видов» (1859).
Дарвиновская модель утверждает, что случайные изменения, возникающие при передаче признаков между поколениями, могут приводить к естественному отбору. Выживают и оставляют потомство те организмы, чьи свойства наилучшим образом соответствуют окружающей среде, в результате чего признаки, повышающие приспособленность, накапливаются и наследуются. Однако сам Дарвин не мог объяснить механизм наследования, поскольку работал за десятилетия до появления генетики.
Несмотря на название, книга Дарвина не объясняет происхождение видов, поскольку сценарий возникновения нового вида требует появления не менее сотни совместимых особей — что делает такой процесс крайне маловероятным при случайных мутациях.
Теория Дарвина также не учитывает наблюдаемую системность в разнообразии живых форм, такую как закон гомологических рядов Н. И. Вавилова. Это побудило исследователей к поиску альтернатив: так, Л. С. Берг предложил концепцию номогенеза — закономерной, направленной эволюции, которую развил А. А. Любищев, предполагая математическую основу формообразования.
Тем не менее, именно модель Дарвина легла в основу генетических алгоритмов (ГА). Эти алгоритмы воспроизводят основные принципы дарвиновской эволюции: изменчивость, отбор, наследование. При этом ГА не моделируют отдельных особей, а работают с популяциями, стремясь к формированию решений, наиболее приспособленных к заданным условиям.
Таким образом, генетические алгоритмы можно рассматривать как имитационные модели различных теорий эволюции, и сопоставление их результатов с реальной историей жизни может способствовать поиску более адекватной эволюционной теории.
Несмотря на то, что биологи пока не пришли к единой системе критериев, позволяющей оценивать значимость процессов, воспроизводимых в ГА, такие алгоритмы всё же представляют собой важный инструмент концептуального анализа и экспериментальной проверки эволюционных гипотез.
Пример работы простого генетического алгоритма представлен на блок-схеме
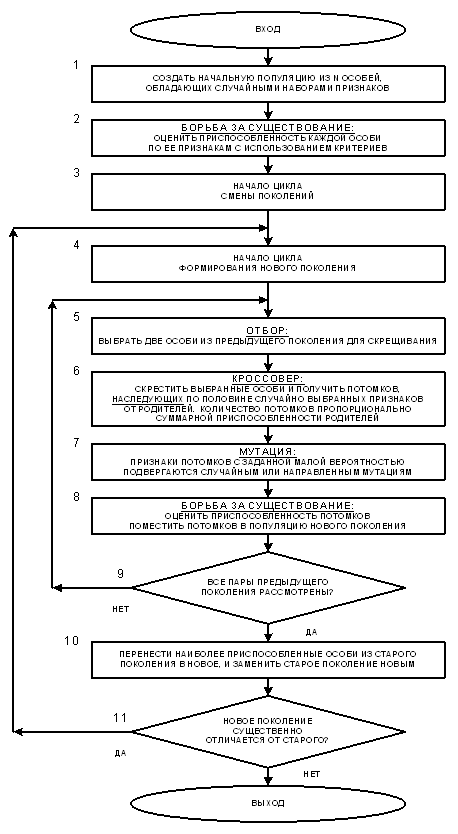
Работа генетического алгоритма (ГА) представляет собой итерационный процесс, который продолжается до тех пор, пока поколения не перестанут существенно отличаться друг от друга, или не пройдет заданное количество поколений, или заданное время. Для каждого поколения реализуются отбор, кроссовер (скрещивание) и мутация. Рассмотрим этот алгоритм.
Шаг 1: Начальная популяция
Генерируется начальная популяция, состоящая из N особей со случайными наборами признаков.
Шаг 2: Борьба за существование
Вычисляется абсолютная приспособленность каждой особи популяции к условиям среды f(i) и суммарная приспособленность популяции.
Затем при пропорциональном отборе для каждой особи вычисляется её относительный вклад Ps(i):
(3)
Ps(i) = f(i) / ∑ f(i)
В выражении (3) можно сравнивать f(i) со средней абсолютной приспособленностью:
(4)
f_avg = ∑ f(i) / N
Тогда получим:
(5)
Ps(i) = f(i) / f_avg
Если взять логарифм по основанию 2 от выражения (5), то получим количество информации, содержащееся в признаках особи:
(6)
I(i) = log₂(f(i) / f_avg)
Эта формула совпадает с формулой для семантического количества информации Харкевича, если целью считать индивидуальное выживание и продолжение рода.
Интерпретация количества информации:
- Положительное значение — особь выживает и даёт потомство, численность которого пропорциональна информации.
- Ноль — особь доживает до зрелости, но не размножается.
- Отрицательное значение — особь погибает до зрелости.
Вывод: естественный отбор — это процесс генерации и накопления информации о выживании и продолжении рода в популяции как системе.
Это накопление происходит на разных уровнях:
- Элементы: отдельные особи.
- Связи: отношения между особями.
- Цель системы: сохранение и развитие популяции через индивидуальные цели особей.
Фенотип и взаимодействие
Фенотип соответствует генотипу и отражает внешние признаки особи. Взаимодействие с окружающей средой через фенотип определяет, будет ли особь передавать гены потомству.
Шаг 3: Начало цикла смены поколений
Шаг 4: Начало формирования нового поколения
Шаг 5: Отбор
Осуществляется пропорциональный отбор. Выбираются особи с положительным количеством информации; вероятность выбора пропорциональна информации.
Шаг 6: Кроссовер
С вероятностью Pc происходит скрещивание. Потомки получают случайные признаки от родителей. Численность потомков зависит от суммарной приспособленности родителей.
Если кроссовер не происходит — особи переходят к мутации.
Шаг 7: Мутация
С вероятностью Pm признаки потомков случайным образом изменяются. Механизм роднит ГА с методом Монте-Карло.
Шаг 8: Борьба за существование
Оценивается приспособленность потомков — как на шаге 2.
Шаг 9: Проверка потомства
Если не все отобранные особи дали потомство — возврат к шагу 5.
Шаг 10: Смена поколений
- Потомки формируют новое поколение.
- Самые приспособленные особи из предыдущего поколения могут быть перенесены (ограниченное число раз).
- Новая популяция замещает старую.
Шаг 11: Условие останова
Алгоритм завершается, если:
- Поколения перестают отличаться (сходимость);
- Превышено количество поколений или времени.
Если ГА сошёлся — найдено решение, т.е. популяция адаптирована к среде.
Иначе — возврат к шагу 4.
Пример работы алгоритма для поиска максиума:
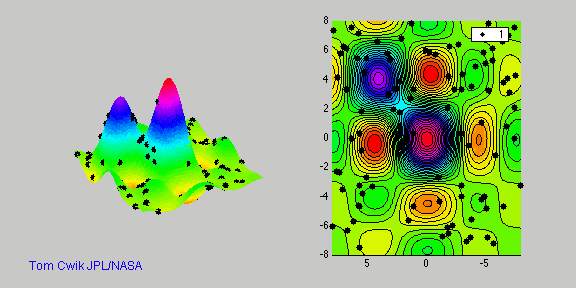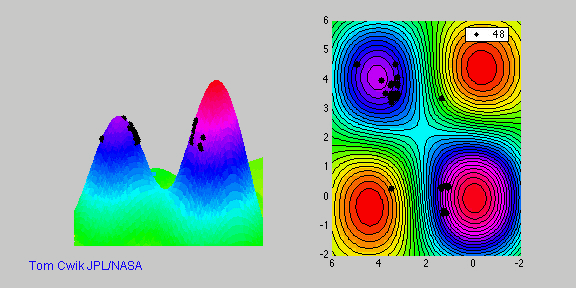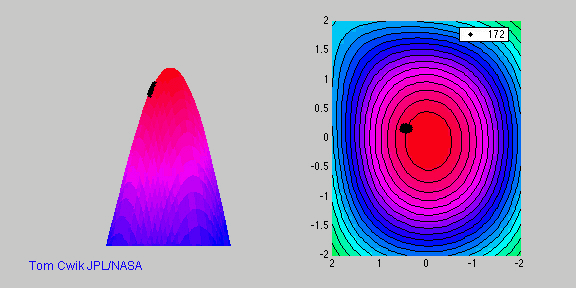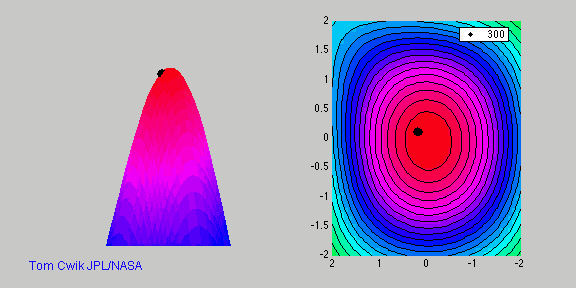
Разнообразие реализаций ГА
Реальные ГА отличаются от базового варианта. Исследователи варьируют:
- Методы отбора;
- Критерии приспособленности;
- Передачу рецессивных признаков;
- Виды мутаций;
- Стратегии скрещивания и отбора.
ГА — это не единый алгоритм, а широкий класс методов.
Популярные операторы отбора:
- Турнирный отбор (Brindle, 1981; Goldberg и Deb, 1991) — из k особей выбирается лучшая. Обычно k = 2.
- Элитный отбор (De Jong, 1975) — сохраняется одна лучшая особь.
- Двухточечный кроссовер (Cavicchio, 1970; Goldberg, 1989c).
- Равномерный кроссовер (Syswerda, 1989).
Несмотря на упрощения по сравнению с природной эволюцией, ГА — мощный инструмент, применимый в широком классе прикладных задач, особенно там, где другие методы бессильны.
Практическая реализация генетического алгоритма#
Постановка задачи
Задача программы — с помощью генетического алгоритма автоматически подобрать строку, которая в точности совпадает с заданной целевой строкой Hello world!, используя только операции случайной генерации, скрещивания и мутации символов.
import random
import string
# Целевая строка
TARGET = "Hello world!"
# Размер популяции
POPULATION_SIZE = 100
# Вероятность мутации
MUTATION_RATE = 0.01
# Символы, которые могут использоваться
CHARS = string.printable
def random_string(length):
return ''.join(random.choice(CHARS) for _ in range(length))
def fitness(individual):
return sum(1 for expected, actual in zip(TARGET, individual) if expected == actual)
def mutate(individual):
return ''.join(
c if random.random() > MUTATION_RATE else random.choice(CHARS)
for c in individual
)
def crossover(parent1, parent2):
split = random.randint(0, len(TARGET))
return parent1[:split] + parent2[split:]
# Инициализация популяции
population = [random_string(len(TARGET)) for _ in range(POPULATION_SIZE)]
generation = 0
while True:
# Оценка приспособленности
population = sorted(population, key=fitness, reverse=True)
best = population[0]
print(f"Gen {generation}: {best} (fitness: {fitness(best)})")
if best == TARGET:
break
# Отбор лучших и создание новой популяции
new_population = population[:2] # Элитизм: сохранить лучших
while len(new_population) < POPULATION_SIZE:
parents = random.choices(population[:50], k=2) # Скрещивать лучших
child = mutate(crossover(*parents))
new_population.append(child)
population = new_population
generation += 1
Разберем основные элементы кода генетичесокго алгоритма
const std::string TARGET = "Hello world!";
const int POPULATION_SIZE = 100;
const double MUTATION_RATE = 0.01;
Константы и настройки. Задают целевую строку, размер популяции и вероятность мутации.
std::string random_string(size_t length);
Генерация случайной строки. Создаёт случайную строку из допустимых символов.
int fitness(const std::string& individual);
Оценка приспособленности. Подсчитывает количество совпадающих символов с целевой строкой.
std::string mutate(const std::string& individual);
Мутация. Случайно изменяет отдельные символы с заданной вероятностью.
std::string crossover(const std::string& parent1, const std::string& parent2);
Скрещивание Создаёт потомка, объединяя части двух родителей.
while (true) {
// сортировка, отбор, создание новой популяции
}
Цикл поколений:
- Сортировка по приспособленности
- Вывод лучшего результата
- Отбор лучших и генерация потомков
- Завершение при совпадении с TARGET
Полный код программы предсатвлен ниже
#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
#include <random>
#include <ctime>
const std::string TARGET = "Hello world!";
const int POPULATION_SIZE = 100;
const double MUTATION_RATE = 0.01;
const std::string CHARS =
"0123456789abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ!\"#$%&'()*+,-./:;<=>?@[\\]^_`{|}~ \t\n\r\x0b\x0c";
// Генератор случайных чисел
std::mt19937 rng(std::time(nullptr));
std::uniform_real_distribution<double> mutation_dist(0.0, 1.0);
std::uniform_int_distribution<int> char_dist(0, CHARS.size() - 1);
std::uniform_int_distribution<int> crossover_dist(0, TARGET.size());
std::string random_string(size_t length) {
std::string s;
for (size_t i = 0; i < length; ++i) {
s += CHARS[char_dist(rng)];
}
return s;
}
int fitness(const std::string& individual) {
int score = 0;
for (size_t i = 0; i < TARGET.size(); ++i) {
if (i < individual.size() && individual[i] == TARGET[i]) {
++score;
}
}
return score;
}
std::string mutate(const std::string& individual) {
std::string result = individual;
for (char& c : result) {
if (mutation_dist(rng) < MUTATION_RATE) {
c = CHARS[char_dist(rng)];
}
}
return result;
}
std::string crossover(const std::string& parent1, const std::string& parent2) {
int split = crossover_dist(rng);
return parent1.substr(0, split) + parent2.substr(split);
}
int main() {
std::vector<std::string> population;
for (int i = 0; i < POPULATION_SIZE; ++i) {
population.push_back(random_string(TARGET.size()));
}
int generation = 0;
while (true) {
// Сортировка по убыванию приспособленности
std::sort(population.begin(), population.end(), [](const std::string& a, const std::string& b) {
return fitness(a) > fitness(b);
});
const std::string& best = population[0];
std::cout << "Gen " << generation << ": " << best << " (fitness: " << fitness(best) << ")\n";
if (best == TARGET) {
break;
}
std::vector<std::string> new_population = { population[0], population[1] };
std::uniform_int_distribution<int> parent_dist(0, 49); // топ-50
while (new_population.size() < POPULATION_SIZE) {
const std::string& parent1 = population[parent_dist(rng)];
const std::string& parent2 = population[parent_dist(rng)];
std::string child = mutate(crossover(parent1, parent2));
new_population.push_back(child);
}
population = new_population;
++generation;
}
return 0;
}
Задание
Модифицируйте исходный код генетического алгоритма, который отгадывает строку, так, чтобы он угадывал целое число фиксированной длины, введённое пользователем.
На вход алгоритм берет число n - количество цифр в угадываемом числе m. Далее следует число m.
Функция приспособленности должна измерять расстояние следующим образом: fitness(individual) = abs(int(TARGET) - int(individual))
Цель — минимизировать это значение (чем ближе к 0, тем лучше).
Алгоритм должен завершиться, когда кандидат совпадает с целевым числом (расстояние = 0).
Не в силах эволюционировать сами, заставим эволюционировать других#
Придумаем простенькую игру:
- Есть шарик, который может двигаться влево, вправо, вверх, вниз
- Есть игровое поле высотой h и w
- Есть квадрат, расположеннный по координатам х0, y0, x1,y1, которого необходимо достичь в ходе эволюции

import pygame
import random
import math
import sys
pygame — для отрисовки и обработки графики.
random — для генерации случайных чисел (мутация, начальные гены).
math — математические функции (здесь почти не используется).
sys — для выхода из программы.
WIDTH, HEIGHT = 800, 600
AGENT_RADIUS = 4
GOAL = pygame.Vector2(WIDTH // 2, 50)
GENE_LENGTH = 200
POP_SIZE = 100
MUTATION_RATE = 0.01
MAX_SPEED = 4
fps = 60
Размеры экрана (WIDTH, HEIGHT)
Радиус агента (AGENT_RADIUS)
Цель (GOAL) в верхней части экрана
Длина "гена" (количество шагов движения)
Размер популяции (POP_SIZE)
Вероятность мутации (MUTATION_RATE)
Максимальная скорость агента (MAX_SPEED)
Опишем класс, отвечающий за работу с генами (Класс DNA)
class DNA:
def __init__(self, genes=None):
if genes:
self.genes = genes
else:
self.genes = [pygame.Vector2(random.uniform(-1, 1), random.uniform(-1, 1)).normalize() * MAX_SPEED for _ in range(GENE_LENGTH)]
def crossover(self, partner):
new_genes = []
for i in range(len(self.genes)):
if i % 2 == 0:
new_genes.append(self.genes[i])
else:
new_genes.append(partner.genes[i])
return DNA(new_genes)
def mutate(self):
for i in range(len(self.genes)):
if random.random() < MUTATION_RATE:
self.genes[i] = pygame.Vector2(random.uniform(-1, 1), random.uniform(-1, 1)).normalize() * MAX_SPEED
Объяснение:
Гены представлены как список векторов скорости
Кроссовер: смешение генов родителей (чередование)
Мутация: случайное изменение генов с заданной вероятностью
Опишем класс, описывающий кажду особь в популяции отдельно
class Agent:
def __init__(self, dna=None):
self.pos = pygame.Vector2(WIDTH // 2, HEIGHT - 50)
self.vel = pygame.Vector2(0, 0)
self.acc = pygame.Vector2(0, 0)
self.dna = dna if dna else DNA()
self.fitness = 0
self.step = 0
self.reached_goal = False
def apply_force(self, force):
self.acc += force
def update(self):
if not self.reached_goal and self.step < GENE_LENGTH:
self.apply_force(self.dna.genes[self.step])
self.step += 1
self.vel += self.acc
if self.vel.length() > MAX_SPEED:
self.vel.scale_to_length(MAX_SPEED)
self.pos += self.vel
self.acc *= 0
if self.pos.distance_to(GOAL) < 10:
self.reached_goal = True
def calc_fitness(self):
distance = self.pos.distance_to(GOAL)
self.fitness = 1 / (distance + 1)
def draw(self, screen):
pygame.draw.circle(screen, (0, 255, 0), (int(self.pos.x), int(self.pos.y)), AGENT_RADIUS)
Позиция стартует снизу экрана
Обновление позиции по генам (последовательность движений)
Фитнес-функция: обратная зависимость от расстояния до цели
Введем Класс Population - описающий действия над всей попляцией
class Population:
def __init__(self):
self.agents = [Agent() for _ in range(POP_SIZE)]
self.generation = 1
self.mating_pool = []
self.best_fitness = 0
def update(self):
for agent in self.agents:
agent.update()
def draw(self, screen):
for agent in self.agents:
agent.draw(screen)
def evaluate(self):
max_fitness = 0
for agent in self.agents:
agent.calc_fitness()
if agent.fitness > max_fitness:
max_fitness = agent.fitness
self.best_fitness = max_fitness
self.mating_pool.clear()
for agent in self.agents:
n = int((agent.fitness / max_fitness) * 100)
self.mating_pool += [agent] * n
def reproduce(self):
new_agents = []
for _ in range(POP_SIZE):
parent_a = random.choice(self.mating_pool)
parent_b = random.choice(self.mating_pool)
child_dna = parent_a.dna.crossover(parent_b.dna)
child_dna.mutate()
new_agents.append(Agent(child_dna))
self.agents = new_agents
self.generation += 1
Создание пула для размножения пропорционально фитнесу
Селекция: случайный выбор родителей из пула
Генетические операции: кроссовер + мутация
Создание нового поколения
Наконец основной цикл + отрисовка параметров
def draw_info(screen, population):
texts = [
f"Поколение: {population.generation}",
f"Лучший фитнес: {population.best_fitness:.4f}",
f"Популяция: {POP_SIZE}",
f"Мутация: {MUTATION_RATE*100:.1f}%",
f"Скорость симуляции (FPS): {fps}"
]
for i, text in enumerate(texts):
render = font.render(text, True, (255, 255, 255))
screen.blit(render, (10, 10 + i * 22))
population = Population()
frame = 0
while True:
screen.fill((30, 30, 30))
pygame.draw.circle(screen, (255, 0, 0), (int(GOAL.x), int(GOAL.y)), 10)
for event in pygame.event.get():
if event.type == pygame.QUIT:
pygame.quit()
sys.exit()
elif event.type == pygame.KEYDOWN:
if event.key == pygame.K_v:
fps = min(fps + 10, 240)
elif event.key == pygame.K_d:
fps = max(fps - 10, 1)
if frame < GENE_LENGTH:
population.update()
frame += 1
else:
population.evaluate()
population.reproduce()
frame = 0
population.draw(screen)
draw_info(screen, population)
pygame.display.flip()
clock.tick(fps)
#include <SFML/Graphics.hpp>
#include <vector>
#include <cmath>
#include <random>
#include <ctime>
#include <string>
#include <sstream>
const int WIDTH = 800;
const int HEIGHT = 600;
const int AGENT_RADIUS = 4;
const int GENE_LENGTH = 200;
const int POP_SIZE = 100;
const float MUTATION_RATE = 0.01f;
const float MAX_SPEED = 4.0f;
sf::Vector2f GOAL(WIDTH / 2, 50);
std::mt19937 rng(static_cast<unsigned>(time(nullptr)));
std::uniform_real_distribution<float> distFloat(-1.f, 1.f);
std::uniform_real_distribution<float> dist01(0.f, 1.f);
Алгоритм, как обычно наичнается с контанты и их инциализации
Здесь задаются основные параметры программы, такие как размеры окна (WIDTH, HEIGHT), радиус агентов (AGENT_RADIUS), количество шагов для движения (GENE_LENGTH), размер популяции (POP_SIZE), коэффициент мутации (MUTATION_RATE) и максимальная скорость агентов (MAX_SPEED).
Также создается цель, к которой агенты должны стремиться (GOAL). Для генерации случайных чисел используется генератор случайных чисел и два распределения:
distFloat: для случайных координат.
dist01: для вероятностей (например, мутации).
sf::Vector2f randomVector2D() {
sf::Vector2f v(distFloat(rng), distFloat(rng));
float len = std::sqrt(v.x * v.x + v.y * v.y);
if (len > 0) v *= MAX_SPEED / len;
return v;
}
Эта функция генерирует случайный вектор с нормированным направлением. Она используется для создания случайных генов агентов.
class DNA {
public:
std::vector<sf::Vector2f> genes;
DNA() {
genes.resize(GENE_LENGTH);
for (auto& gene : genes) gene = randomVector2D();
}
DNA crossover(const DNA& partner) const {
DNA child;
for (size_t i = 0; i < genes.size(); ++i) {
child.genes[i] = (i % 2 == 0) ? genes[i] : partner.genes[i];
}
return child;
}
void mutate() {
for (auto& gene : genes) {
if (dist01(rng) < MUTATION_RATE)
gene = randomVector2D();
}
}
};
Класс DNA представляет генетическую информацию агента:
Конструктор генерирует случайные гены (вектора).
Метод crossover выполняет операцию скрещивания двух ДНК, комбинируя гены из двух партнеров.
Метод mutate случайным образом изменяет гены с вероятностью, определенной мутацией.
class Agent {
public:
sf::Vector2f pos, vel, acc;
DNA dna;
int step = 0;
float fitness = 0;
bool reachedGoal = false;
Agent(const DNA& d = DNA()) : pos(WIDTH / 2, HEIGHT - 50), dna(d) {}
void applyForce(const sf::Vector2f& f) { acc += f; }
void update() {
if (reachedGoal || step >= GENE_LENGTH) return;
applyForce(dna.genes[step++]);
vel += acc;
float speed = std::sqrt(vel.x * vel.x + vel.y * vel.y);
if (speed > MAX_SPEED) vel *= MAX_SPEED / speed;
pos += vel;
acc *= 0.f;
if (std::hypot(pos.x - GOAL.x, pos.y - GOAL.y) < 10)
reachedGoal = true;
}
void calcFitness() {
float d = std::hypot(pos.x - GOAL.x, pos.y - GOAL.y);
fitness = 1.0f / (d + 1);
}
void draw(sf::RenderWindow& win) const {
sf::CircleShape c(AGENT_RADIUS);
c.setFillColor(sf::Color::Green);
c.setPosition(pos - sf::Vector2f(AGENT_RADIUS, AGENT_RADIUS));
win.draw(c);
}
};
Класс Agent представляет собой агента, который имеет следующие параметры:
Позиция (pos), скорость (vel), ускорение (acc).
ДНК (через объект класса DNA).
Шаг в генах (step) и фитнес агента (fitness), который определяет, насколько близок агент к цели.
Метод applyForce добавляет силу к ускорению.
Метод update обновляет состояние агента: передвижение по шагам генов и проверка достижения цели.
Метод calcFitness вычисляет фитнес на основе расстояния до цели.
Метод draw рисует агента.
class Population {
public:
std::vector<Agent> agents;
int generation = 1;
float bestFitness = 0;
std::vector<Agent*> matingPool;
Population() {
agents.resize(POP_SIZE);
}
void update() {
for (auto& a : agents) a.update();
}
void draw(sf::RenderWindow& win) {
for (auto& a : agents) a.draw(win);
}
void evaluate() {
bestFitness = 0;
matingPool.clear();
for (auto& a : agents) {
a.calcFitness();
if (a.fitness > bestFitness) bestFitness = a.fitness;
}
for (auto& a : agents) {
int n = static_cast<int>((a.fitness / bestFitness) * 100);
for (int i = 0; i < n; ++i) matingPool.push_back(&a);
}
}
void reproduce() {
std::vector<Agent> newAgents;
newAgents.reserve(POP_SIZE);
for (int i = 0; i < POP_SIZE; ++i) {
Agent* p1 = matingPool[rng() % matingPool.size()];
Agent* p2 = matingPool[rng() % matingPool.size()];
DNA childDNA = p1->dna.crossover(p2->dna);
childDNA.mutate();
newAgents.emplace_back(childDNA);
}
agents = std::move(newAgents);
generation++;
}
};
Класс Population представляет популяцию агентов:
Метод update обновляет всех агентов в популяции.
Метод draw рисует всех агентов на экране.
Метод evaluate вычисляет фитнес всех агентов и формирует пул для спаривания.
Метод reproduce создает новое поколение агентов через операцию кроссовера и мутации.
void drawInfo(sf::RenderWindow& win, sf::Font& font, int gen, float bestFitness, int popSize, float mutRate, int fps) {
std::ostringstream oss;
oss << "Поколение: " << gen << "\nЛучший фитнес: " << bestFitness
<< "\nПопуляция: " << popSize << "\nМутация: " << mutRate * 100 << "%"
<< "\nFPS: " << fps;
sf::Text text(oss.str(), font, 16);
text.setFillColor(sf::Color::White);
text.setPosition(10, 10);
win.draw(text);
}
Эта функция отображает текущую информацию на экране: номер поколения, лучший фитнес, размер популяции, вероятность мутации и текущий FPS.
int main() {
sf::RenderWindow window(sf::VideoMode(WIDTH, HEIGHT), "Генетический алгоритм SFML");
window.setFramerateLimit(60);
sf::Font font;
if (!font.loadFromFile("arial.ttf")) return 1;
Population population;
int frame = 0;
int fps = 60;
while (window.isOpen()) {
sf::Event e;
while (window.pollEvent(e)) {
if (e.type == sf::Event::Closed)
window.close();
if (e.type == sf::Event::KeyPressed) {
if (e.key.code == sf::Keyboard::V)
fps = std::min(240, fps + 10);
else if (e.key.code == sf::Keyboard::D)
fps = std::max(1, fps - 10);
window.setFramerateLimit(fps);
}
}
window.clear(sf::Color(30, 30, 30));
sf::CircleShape goal(10);
goal.setFillColor(sf::Color::Red);
goal.setPosition(GOAL - sf::Vector2f(10, 10));
window.draw(goal);
if (frame < GENE_LENGTH) {
population.update();
++frame;
}
else {
population.evaluate();
population.reproduce();
frame = 0;
}
population.draw(window);
drawInfo(window, font, population.generation, population.bestFitness, POP_SIZE, MUTATION_RATE, fps);
window.display();
}
return 0;
}
Основная часть программы создает окно, обрабатывает события (например, изменение FPS с помощью клавиш), обновляет и рисует популяцию агентов, а также отображает информацию о состоянии симуляции.

Задание
Модифицируйте исходный код, изменив метод calc_fitness (python)
- self.fitness = math.exp(-distance)
- self.fitness = 1 / (distance * distance + 1)
- self.fitness = math.exp(-distance ** 2 / (2 * sigma ** 2))
Что меняется?
- Попробуйте реализовать теперь функицю, которая награждает не толко за близость к цели, но и за минимальное количество шагов.
Модифицируйте исходный код, изменив метод calcFitness() (С++)
- fitness = std::exp(-distance);
- fitness = 1.0f / (distance * distance + 1.0f);
- float sigma = 100.0f; fitness = std::exp(- (distance * distance) / (2.0f * sigma * sigma));
Что меняется?
- Попробуйте реализовать теперь функицю, которая награждает не толко за близость к цели, но и за минимальное количество шагов.
Муравиный алгоритм#
Муравьиный алгоритм (Ant Colony Optimization, ACO) — это метаэвристический метод для решения задач оптимизации, вдохновленный поведением муравьев в поиске пищи. Алгоритм был разработан в 1992 году Марко Дориги и его коллегами, и с тех пор широко применяется для решения различных задач, таких как задача коммивояжера (TSP), расписания, оптимизация маршрутов и др.
Основные идеи#
- Поведение муравьев: Муравьи находит кратчайший путь к пище, следуя за феромонами, которые они оставляют на пути.
- Феромоны: Муравьи оставляют следы феромонов на пройденном пути. Эти следы испаряются со временем, но феромоны остаются на пути, по которому прошел муравей.
- Алгоритм: Исключает полное переборное решение. Вместо этого множество агентов (муравьев) исследуют пространство решений параллельно, используя феромоны для принятия решений.
- Использование феромонов: Пути, по которым проходит больше муравьев, становятся более привлекательными для других муравьев, так как оставшиеся феромоны усиливаются.
Шаги работы алгоритма#
- Инициализация: Инициализация феромонов на всех путях с равными значениями.
- Построение решения: Каждый муравей строит решение, выбирая следующий шаг на основе вероятности, которая зависит от количества феромонов и длины пути.
- Обновление феромонов:
- Феромоны испаряются со временем (уменьшаются).
- Добавляются новые феромоны на пути, пройденные муравьями. Чем лучше путь, тем больше феромонов добавляется.
- Повторение: Алгоритм повторяется, пока не будет найдено оптимальное решение или не исчерпано количество итераций.
Параметры алгоритма#
- Количество муравьев: Количество агентов, которые будут искать решение.
- Испарение феромонов: Коэффициент, определяющий скорость, с которой феромоны исчезают со времени.
- Параметры α и β: Они контролируют влияние феромонов (α) и расстояния (β) на выбор пути.
- Число итераций: Количество циклов, в которых муравьи будут искать решение.
Муравьиный алгоритм применим для различных задач:
- Задача коммивояжера (TSP): Поиск кратчайшего пути, который посещает все города.
- Оптимизация маршрута: Для логистики и доставки товаров.
- Распределение задач: Например, при решении задачи о распорядке работы оборудования.
Пример использования#
Пример использования муравьиного алгоритма для решения задачи коммивояжера (TSP) приведен ниже.
import random
import numpy as np
# Матрица расстояний (граф с 4 вершинами)
distances = np.array([
[0, 2, 2, 5],
[2, 0, 3, 4],
[2, 3, 0, 1],
[5, 4, 1, 0]
])
num_ants = 5
num_iterations = 100
alpha = 1 # Влияние феромона
beta = 2 # Влияние расстояния
evaporation = 0.5
pheromone_deposit = 100
n = len(distances)
pheromones = np.ones((n, n)) # начальный феромон
def choose_next_city(current, visited):
probabilities = []
for i in range(n):
if i in visited:
probabilities.append(0)
else:
prob = (pheromones[current][i] ** alpha) * ((1.0 / distances[current][i]) ** beta)
probabilities.append(prob)
total = sum(probabilities)
probabilities = [p / total for p in probabilities]
return random.choices(range(n), weights=probabilities)[0]
def run_ant():
path = [random.randint(0, n - 1)]
while len(path) < n:
next_city = choose_next_city(path[-1], path)
path.append(next_city)
return path
def path_length(path):
return sum(distances[path[i]][path[i + 1]] for i in range(len(path) - 1)) + distances[path[-1]][path[0]]
for iteration in range(num_iterations):
all_paths = [run_ant() for _ in range(num_ants)]
all_lengths = [path_length(p) for p in all_paths]
# Обновляем феромоны
pheromones *= (1 - evaporation)
for i in range(num_ants):
path = all_paths[i]
length = all_lengths[i]
for j in range(len(path) - 1):
a, b = path[j], path[j + 1]
pheromones[a][b] += pheromone_deposit / length
pheromones[b][a] += pheromone_deposit / length
# Выводим лучший путь
best_path = min([run_ant() for _ in range(100)], key=path_length)
print("Лучший путь:", best_path)
print("Длина:", path_length(best_path))
#include <iostream>
#include <vector>
#include <cmath>
#include <limits>
#include <random>
#include <algorithm>
using namespace std;
const int N = 4; // количество городов
const int NUM_ANTS = 5;
const int NUM_ITERATIONS = 100;
const double ALPHA = 1.0; // Влияние феромона
const double BETA = 2.0; // Влияние расстояния
const double EVAPORATION = 0.5;
const double Q = 100.0;
double distances[N][N] = {
{0, 2, 2, 5},
{2, 0, 3, 4},
{2, 3, 0, 1},
{5, 4, 1, 0}
};
double pheromones[N][N];
random_device rd;
mt19937 gen(rd());
int select_next_city(int current, const vector<bool>& visited) {
vector<double> probabilities(N, 0.0);
double sum = 0.0;
for (int i = 0; i < N; ++i) {
if (!visited[i]) {
double tau = pow(pheromones[current][i], ALPHA);
double eta = pow(1.0 / distances[current][i], BETA);
probabilities[i] = tau * eta;
sum += probabilities[i];
}
}
uniform_real_distribution<> dis(0.0, sum);
double r = dis(gen);
double cumulative = 0.0;
for (int i = 0; i < N; ++i) {
if (!visited[i]) {
cumulative += probabilities[i];
if (r <= cumulative) return i;
}
}
// fallback (должно не понадобиться)
for (int i = 0; i < N; ++i)
if (!visited[i]) return i;
return 0;
}
vector<int> run_ant() {
uniform_int_distribution<> dis(0, N - 1);
int start = dis(gen);
vector<int> path = {start};
vector<bool> visited(N, false);
visited[start] = true;
while (path.size() < N) {
int next = select_next_city(path.back(), visited);
path.push_back(next);
visited[next] = true;
}
return path;
}
double path_length(const vector<int>& path) {
double length = 0.0;
for (int i = 0; i < path.size() - 1; ++i)
length += distances[path[i]][path[i + 1]];
length += distances[path.back()][path[0]]; // возвращение в начало
return length;
}
int main() {
// Инициализация феромонов
for (int i = 0; i < N; ++i)
for (int j = 0; j < N; ++j)
pheromones[i][j] = 1.0;
for (int iter = 0; iter < NUM_ITERATIONS; ++iter) {
vector<vector<int>> all_paths(NUM_ANTS);
vector<double> lengths(NUM_ANTS);
for (int k = 0; k < NUM_ANTS; ++k) {
all_paths[k] = run_ant();
lengths[k] = path_length(all_paths[k]);
}
// Испарение феромонов
for (int i = 0; i < N; ++i)
for (int j = 0; j < N; ++j)
pheromones[i][j] *= (1.0 - EVAPORATION);
// Добавление феромонов
for (int k = 0; k < NUM_ANTS; ++k) {
double contribution = Q / lengths[k];
const auto& path = all_paths[k];
for (int i = 0; i < N - 1; ++i) {
int a = path[i];
int b = path[i + 1];
pheromones[a][b] += contribution;
pheromones[b][a] += contribution;
}
// возврат в начало
pheromones[path.back()][path[0]] += contribution;
pheromones[path[0]][path.back()] += contribution;
}
}
// Поиск лучшего пути после обучения
double best_length = numeric_limits<double>::max();
vector<int> best_path;
for (int i = 0; i < 100; ++i) {
auto path = run_ant();
double len = path_length(path);
if (len < best_length) {
best_length = len;
best_path = path;
}
}
cout << "Лучший путь: ";
for (int city : best_path)
cout << city << " ";
cout << best_path[0] << endl; // возвращение
cout << "Длина: " << best_length << endl;
return 0;
}
Список использованных источников и благодарностей#
- Спасибо за идею реализации генетического алгоритма Luke Garrigan