Практика 13. Эвристические алгоритмы на примере задачи Коммивояжера. Метод отжига.#
Повторение практики 12.#
Метод ветвей и границ#
Этот метод может быть использован не только для задач поиска, но и для задач оптимизации. Допустим, мы решаем задачу минимизации (для задачи максимизации всё аналогично). Как и раньше, мы рассматриваем частичные решения. Нам необходимо понять, какие из них заведомо не приведут к оптимальному решению, чтобы их отбросить и сэкономить время. Отбросить подзадачу можно, если мы знаем, что на этом пути получится решение, худшее уже найденного в другой ветви. Но откуда мы это можем узнать? Для этого надо использовать нижнюю оценку стоимости решения.
S = {P[0]} # {множество активных подзадач}
пока S не пусто:
выбрать подзадачу (частичное решение) P ∈ S и удалить её из S
разбить P на меньшие подзадачи P[1], P[2], ... , P[k]
для каждой P[i]:
если P[i] является полным решением:
обновить текущий_минимум с учётом P[i]
иначе если нижняя_оценка(P[i]) < текущий_минимум:
добавить P[i] в S
вернуть текущий_минимум
Использование эвристик для оптимизации перебора#
Если уж дело дошло до полного перебора, то использование эвристик позволяет ускорить его в некоторых случаях на порядки. Представим себе, что мы можем численно оценить «перспективность» конкретного хода или даже всей позиции целиком. В этом случае позиции для следующего шага нужно перебирать в порядке убывания «качества» этого шага или «качества» получаемой позиции. Если есть возможность оценить качество шага, то удобно использовать перебор с возвратом в виде
def Перебор(Ситуация):
if Ситуация конечная:
Завершающая обработка
else:
for Действие in Множество_всех_возможных_действий,_упорядоченное_по_убыванию_перспективности:
Применить Действие к Ситуация
Перебор(Ситуация)
откатить Действие назад
Если есть возможность оценить «перспективность» позиции целиком, то может оказаться удобно использовать очередь заданий. Соберём все возможные пары (перспективность, задание) в список и отсортируем его. Каждый раз будем удалять из списка самое перспективное задание. Варианты продолжения будем класть назад, поддерживая сортировку (например, используя бинпоиск или bisect.insort, или даже кучу). Итоговый псевдокод получается таким:
задания = [(перспективность_начального_условия, начальное_условие)]
while задания:
текущее = задания.pop()
разбить текущее на меньшие подзадачи P[1], P[2], ... , P[k] (или перебрать все возможные продолжения)
для каждой P[i]:
если тест(P[i]) = успех:
вернуть найденное решение
если тест(P[i]) = неудача:
отбросить P[i]
иначе:
добавить пару (перспективность_P[i], P[i]) в задания
сообщить, что решения нет
Самое сложное — это найти подходящую эвристическую оценку перспективности хода или позиции.
Если мы пытаемся пройти через все вершины в графе, то полезно начинать с вершин, из которой меньше всего выходов.
Если мы пытаемся найти короткий путь в графе, то в качестве оценки позиции можно использовать сумму пройденного пути и эвристической оценки оставшейся части пути.
Если мы пытаемся решить головоломку за минимальное число шагов, то в качестве оценки позиции можно использовать сумму числа уже выполненных ходов и эвристической оценки качества получаемой позиции. При этом для оценки качества позиции можно использовать число шагов для решения задачи по каким-нибудь другим более простым и наглым правилам.
Алгоритм Литтла#
Алгоритм Литтла является частным случаем МВиГ (метод ветвей и границ), т.е. в худшем случае его сложность равна сложности полного перебора. Теоретическое описание выглядит следующим образом:
Имеется множество S всех гамильтоновых циклов графа. На каждом шаге в S ищется ребро (i, j), исключение которого из маршрута максимально увеличит оценку снизу. Далее происходит разбиение множества на два непересекающихся S1 и S2. S1 — все циклы, содержащие ребро (i, j) и не содержащие (j, i). S2 — все циклы, не содержащие (i, j).
Далее вычисляется оценка снизу для длины пути каждого множества и, если она превышает длину уже найденного решения, множество отбрасывается. Если нет — множества S1 и S2 обрабатываются так же, как и S.

Алгоритмическое описание#
Имеется матрица расстояний M. Диагональ заполняется бесконечными значениями, т.к. не должно возникать преждевременных циклов. Также имеется переменная, хранящая нижнюю границу.
Стоит оговориться, что нужно вести учет двух видов бесконечностей — одна добавляется после удаления строки и столбца из матрицы, чтобы не возникало преждевременных циклов, другая — при отбрасывании ребер. Случаи будут рассмотрены чуть позже. Первую бесконечность обозначим как inf1, вторую — inf2. Диагональ заполнена inf1.
Алгоритм состоит из двух этапов:
Первый этап
Приведение матрицы затрат и вычисление нижней оценки стоимости маршрута r.
- Вычисляем наименьший элемент в каждой строке (константа приведения для строки)
- Переходим к новой матрице затрат, вычитая из каждой строки ее константу приведения
- Вычисляем наименьший элемент в каждом столбце (константа приведения для столбца)
- Переходим к новой матрице затрат, вычитая из каждого столбца его константу приведения.
Как результат имеем матрицу затрат, в которой в каждой строчке и в каждом столбце имеется хотя бы один нулевой элемент. - Вычисляем границу на данном этапе как сумму констант приведения для столбцов и строк (данная граница будет являться стоимостью, меньше которой невозможно построить искомый маршрут)
Второй этап
1 .Вычисление штрафа за неиспользование для каждого нулевого элемента приведенной матрицы затрат.
Штраф за неиспользование элемента с индексом (h,k) в матрице, означает, что это ребро не включается в наш маршрут, а значит минимальная стоимость «неиспользования» этого ребра равна сумме минимальных элементов в строке h и столбце k.
а) Ищем все нулевые элементы в приведенной матрице
б) Для каждого из них считаем его штраф за неиспользование.
в) Выбираем элемент, которому соответствует максимальный штраф (любой, если их несколько)
2 . Теперь наше множество S разбиваем на множества — содержащие ребро с максимальным штрафом(Sw) и не содержащие это ребро(Sw/o).
3 . Вычисление оценок затрат для маршрутов, входящих в каждое из этих множеств.
а) Для множества Sw/o все просто: раз мы не берем соответствующее ребро c максимальным штрафом(h,k), то для него оценка затрат равна оценки затрат множества S + штраф за неиспользование ребра (h,k)
б) При вычислении затрат для множества Sw примем во внимание, что раз ребро (h,k) входит в маршрут, то значит ребро (k,h) в маршрут входить не может, поэтому в матрице затрат пишем c(k,h)=infinity, а так как из пункта h мы «уже ушли», а в пункт k мы «уже пришли», то ни одно ребро, выходящее из h, и ни одно ребро, приходящее в k, уже использоваться не могут, поэтому вычеркиваем из матрицы затрат строку h и столбец k. После этого приводим матрицу, и тогда оценка затрат для Sw равна сумме оценки затрат для S и r(h,k), где r(h,k) — сумма констант приведения для измененной матрицы затрат.
4 . Из всех неразбитых множеств выбирается то, которое имеет наименьшую оценку.
Так продолжаем, пока в матрице затрат не останется одна не вычеркнутая строка и один не вычеркнутый столбец.
Пример#
Примеров в интернете огромное количество, но действительно интересный находится в этой статье с хорошо иллюстированными деревьями (единственная найденная мной статья, в которой также указано про распространенную ошибку, но, к сожалению, в ней недостаточно алгоритмическое описание алгоритма — сначала про матрицы, потом про множества)
Рассмотрим следующую матрицу:
| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| 0 | inf | 20 | 18 | 12 | 8 |
| 1 | 5 | inf | 14 | 7 | 11 |
| 2 | 12 | 18 | inf | 6 | 11 |
| 3 | 11 | 17 | 11 | inf | 12 |
| 4 | 5 | 5 | 5 | 5 | inf |
Шаг 1.1 Реудкция строк
Вычитаем минимальные элементы из каждой строки:
- Строка 0: min=8.00
- Строка 1: min=5.00
- Строка 2: min=6.00
- Строка 3: min=11.00
- Строка 4: min=5.00
Результат:
| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| 0 | ∞ | 12.00 | 10.00 | 4.00 | 0.00 |
| 1 | 0.00 | ∞ | 9.00 | 2.00 | 6.00 |
| 2 | 6.00 | 12.00 | ∞ | 0.00 | 5.00 |
| 3 | 0.00 | 6.00 | 0.00 | ∞ | 1.00 |
| 4 | 0.00 | 0.00 | 0.00 | 0.00 | ∞ |
Шаг 1.2 Редукция столбцов
Вычитаем минимальные элементы из каждого столбца:
Столбцы уже содержат нули во всех строках, дополнительная редукция не требуется.
Шаг 1.3 Вычисление оценки
Сумма констант приведения определяет нижнюю границу H:
H = ∑di + ∑dj
H = 8+5+6+11+5+0+0+0+0+0 = 35
Шаг 2 Определение ребра ветвления
Оценки для возможных путей:
| № | (i, j) | Мин по строке | Мин по столбцу | Штраф |
|---|---|---|---|---|
| 1 | (0, 4) | 4 | 1 | 5 |
| 2 | (1, 0) | 2 | 0 | 2 |
| 3 | (2, 3) | 5 | 0 | 5 |
| 4 | (3, 0) | 0 | 0 | 0 |
| 5 | (3, 2) | 0 | 0 | 0 |
| 6 | (4, 0) | 0 | 0 | 0 |
| 7 | (4, 1) | 0 | 6 | 6 |
| 8 | (4, 2) | 0 | 0 | 0 |
| 9 | (4, 3) | 0 | 0 | 0 |
Выбираем ребро (4,1) с наибольшей оценкой.
Шаг 2.1 Ветвление по ребру (4,1)
Удаляем строку 4 и столбец 1:
| 0 | 2 | 3 | 4 | |
|---|---|---|---|---|
| 0 | ∞ | 10.00 | 4.00 | 0.00 |
| 1 | 0.00 | 9.00 | 2.00 | ∞ |
| 2 | 6.00 | ∞ | 0.00 | 5.00 |
| 3 | 0.00 | 0.00 | ∞ | 1.00 |
После вычитания:
| | 0 | 2 | 3 | 4 |
|---|--------|--------|--------|--------|
| 0 | inf1 | 10.00 | 4.00 | 0.00 |
| 1 | 0.00 | 9.00 | 2.00 | inf1 |
| 2 | 6.00 | inf1 | 0.00 | 5.00 |
| 3 | 0.00 | 0.00 | inf1 | 1.00 |
И так далее...
--- Редукция на глубине 0 ---
Матрица до редукции:
['∞', 20.0, 18.0, 12.0, 8.0]
[5.0, '∞', 14.0, 7.0, 11.0]
[12.0, 18.0, '∞', 6.0, 11.0]
[11.0, 17.0, 11.0, '∞', 12.0]
[5.0, 5.0, 5.0, 5.0, '∞']
Минимум в строке 0 = 8.0
Минимум в строке 1 = 5.0
Минимум в строке 2 = 6.0
Минимум в строке 3 = 11.0
Минимум в строке 4 = 5.0
Стоимость редукции = 35.0
Матрица после редукции:
['∞', 12.0, 10.0, 4.0, 0.0]
[0.0, '∞', 9.0, 2.0, 6.0]
[6.0, 12.0, '∞', 0.0, 5.0]
[0.0, 6.0, 0.0, '∞', 1.0]
[0.0, 0.0, 0.0, 0.0, '∞']
Обновленная нижняя граница = 35.0
Выбрано нулевое в (4,1) с максимальным штрафом 6.0
Включить ребро: 4->1
Убрать обратное ребро: 1->4
--- Редукция на глубине 1 ---
Матрица до редукции:
['∞', 10.0, 4.0, 0.0]
[0.0, 9.0, 2.0, '∞']
[6.0, '∞', 0.0, 5.0]
[0.0, 0.0, '∞', 1.0]
Стоимость редукции = 0.0
Матрица после редукции:
['∞', 10.0, 4.0, 0.0]
[0.0, 9.0, 2.0, '∞']
[6.0, '∞', 0.0, 5.0]
[0.0, 0.0, '∞', 1.0]
Обновленная нижняя граница = 35.0
Выбрано нулевое в (3,1) с максимальным штрафом 9.0
Включить ребро: 3->2
Убрать обратное ребро: 2->3
--- Редукция на глубине 2 ---
Матрица до редукции:
['∞', 4.0, 0.0]
[0.0, 2.0, '∞']
[6.0, '∞', 5.0]
Минимум в строке 2 = 5.0
Минимум в столбце 1 = 2.0
Стоимость редукции = 7.0
Матрица после редукции:
['∞', 2.0, 0.0]
[0.0, 0.0, '∞']
[1.0, '∞', 0.0]
Обновленная нижняя граница = 42.0
Выбрано нулевое в (0,2) с максимальным штрафом 2.0
Включить ребро: 0->4
--- Редукция на глубине 3 ---
Матрица до редукции:
[0.0, 0.0]
[1.0, '∞']
Минимум в строке 1 = 1.0
Стоимость редукции = 1.0
Матрица после редукции:
[0.0, 0.0]
[0.0, '∞']
Обновленная нижняя граница = 43.0
Выбрано нулевое в (0,0) с максимальным штрафом 0.0
Включить ребро: 1->0
Исключить ребро: 1->0
--- Редукция на глубине 3 ---
Матрица до редукции:
['∞', 0.0]
[0.0, '∞']
Стоимость редукции = 0.0
Матрица после редукции:
['∞', 0.0]
[0.0, '∞']
Обновленная нижняя граница = 43.0
Выбрано нулевое в (0,1) с максимальным штрафом 0
Включить ребро: 1->3
Исключить ребро: 1->3
--- Редукция на глубине 3 ---
Матрица до редукции:
['∞', '∞']
[0.0, '∞']
Стоимость редукции = 0.0
Матрица после редукции:
['∞', '∞']
[0.0, '∞']
Обновленная нижняя граница = 43.0
Обрезка ветви: нижняя граница превышает текущий лучший результат
Исключить ребро: 0->4
--- Редукция на глубине 2 ---
Матрица до редукции:
['∞', 2.0, '∞']
[0.0, 0.0, '∞']
[1.0, '∞', 0.0]
Минимум в строке 0 = 2.0
Стоимость редукции = 2.0
Матрица после редукции:
['∞', 0.0, '∞']
[0.0, 0.0, '∞']
[1.0, '∞', 0.0]
Обновленная нижняя граница = 44.0
Обрезка ветви: нижняя граница превышает текущий лучший результат
Исключить ребро: 3->2
--- Редукция на глубине 1 ---
Матрица до редукции:
['∞', 10.0, 4.0, 0.0]
[0.0, 9.0, 2.0, '∞']
[6.0, '∞', 0.0, 5.0]
[0.0, '∞', '∞', 1.0]
Минимум в столбце 1 = 9.0
Стоимость редукции = 9.0
Матрица после редукции:
['∞', 1.0, 4.0, 0.0]
[0.0, 0.0, 2.0, '∞']
[6.0, '∞', 0.0, 5.0]
[0.0, '∞', '∞', 1.0]
Обновленная нижняя граница = 44.0
Обрезка ветви: нижняя граница превышает текущий лучший результат
Исключить ребро: 4->1
--- Редукция на глубине 0 ---
Матрица до редукции:
['∞', 12.0, 10.0, 4.0, 0.0]
[0.0, '∞', 9.0, 2.0, 6.0]
[6.0, 12.0, '∞', 0.0, 5.0]
[0.0, 6.0, 0.0, '∞', 1.0]
[0.0, '∞', 0.0, 0.0, '∞']
Минимум в столбце 1 = 6.0
Стоимость редукции = 6.0
Матрица после редукции:
['∞', 6.0, 10.0, 4.0, 0.0]
[0.0, '∞', 9.0, 2.0, 6.0]
[6.0, 6.0, '∞', 0.0, 5.0]
[0.0, 0.0, 0.0, '∞', 1.0]
[0.0, '∞', 0.0, 0.0, '∞']
Обновленная нижняя граница = 41.0
Выбрано нулевое в (3,1) с максимальным штрафом 6.0
Включить ребро: 3->1
Убрать обратное ребро: 1->3
--- Редукция на глубине 1 ---
Матрица до редукции:
['∞', 10.0, 4.0, 0.0]
[0.0, 9.0, '∞', 6.0]
[6.0, '∞', 0.0, 5.0]
[0.0, 0.0, 0.0, '∞']
Стоимость редукции = 0.0
Матрица после редукции:
['∞', 10.0, 4.0, 0.0]
[0.0, 9.0, '∞', 6.0]
[6.0, '∞', 0.0, 5.0]
[0.0, 0.0, 0.0, '∞']
Обновленная нижняя граница = 41.0
Выбрано нулевое в (0,3) с максимальным штрафом 9.0
Включить ребро: 0->4
Убрать обратное ребро: 4->0
--- Редукция на глубине 2 ---
Матрица до редукции:
[0.0, 9.0, '∞']
[6.0, '∞', 0.0]
['∞', 0.0, 0.0]
Стоимость редукции = 0.0
Матрица после редукции:
[0.0, 9.0, '∞']
[6.0, '∞', 0.0]
['∞', 0.0, 0.0]
Обновленная нижняя граница = 41.0
Выбрано нулевое в (0,0) с максимальным штрафом 15.0
Включить ребро: 1->0
--- Редукция на глубине 3 ---
Матрица до редукции:
['∞', 0.0]
[0.0, 0.0]
Стоимость редукции = 0.0
Матрица после редукции:
['∞', 0.0]
[0.0, 0.0]
Обновленная нижняя граница = 41.0
Выбрано нулевое в (0,1) с максимальным штрафом 0.0
Включить ребро: 2->3
Исключить ребро: 2->3
--- Редукция на глубине 3 ---
Матрица до редукции:
['∞', '∞']
[0.0, 0.0]
Стоимость редукции = 0.0
Матрица после редукции:
['∞', '∞']
[0.0, 0.0]
Обновленная нижняя граница = 41.0
Обрезка ветви: нижняя граница превышает текущий лучший результат
Исключить ребро: 1->0
--- Редукция на глубине 2 ---
Матрица до редукции:
['∞', 9.0, '∞']
[6.0, '∞', 0.0]
['∞', 0.0, 0.0]
Минимум в строке 0 = 9.0
Минимум в столбце 0 = 6.0
Стоимость редукции = 15.0
Матрица после редукции:
['∞', 0.0, '∞']
[0.0, '∞', 0.0]
['∞', 0.0, 0.0]
Обновленная нижняя граница = 56.0
Обрезка ветви: нижняя граница превышает текущий лучший результат
Исключить ребро: 0->4
--- Редукция на глубине 1 ---
Матрица до редукции:
['∞', 10.0, 4.0, '∞']
[0.0, 9.0, '∞', 6.0]
[6.0, '∞', 0.0, 5.0]
[0.0, 0.0, 0.0, '∞']
Минимум в строке 0 = 4.0
Минимум в столбце 3 = 5.0
Стоимость редукции = 9.0
Матрица после редукции:
['∞', 6.0, 0.0, '∞']
[0.0, 9.0, '∞', 1.0]
[6.0, '∞', 0.0, 0.0]
[0.0, 0.0, 0.0, '∞']
Обновленная нижняя граница = 50.0
Обрезка ветви: нижняя граница превышает текущий лучший результат
Исключить ребро: 3->1
--- Редукция на глубине 0 ---
Матрица до редукции:
['∞', 6.0, 10.0, 4.0, 0.0]
[0.0, '∞', 9.0, 2.0, 6.0]
[6.0, 6.0, '∞', 0.0, 5.0]
[0.0, '∞', 0.0, '∞', 1.0]
[0.0, '∞', 0.0, 0.0, '∞']
Минимум в столбце 1 = 6.0
Стоимость редукции = 6.0
Матрица после редукции:
['∞', 0.0, 10.0, 4.0, 0.0]
[0.0, '∞', 9.0, 2.0, 6.0]
[6.0, 0.0, '∞', 0.0, 5.0]
[0.0, '∞', 0.0, '∞', 1.0]
[0.0, '∞', 0.0, 0.0, '∞']
Обновленная нижняя граница = 47.0
Обрезка ветви: нижняя граница превышает текущий лучший результат
Best path: [(3, 1), (0, 4), (1, 0), (2, 3), (4, 2)]
Cost: 41.0
Варианты для самостоятельной отработки#
Матрица 1
| | 0 | 1 | 2 | 3 |
|---|----|----|----|----|
| 0 | ∞ | 7 | 3 | 9 |
| 1 | 4 | ∞ | 6 | 2 |
| 2 | 8 | 5 | ∞ | 1 |
| 3 | 2 | 6 | 4 | ∞ |
Матрица 2
| | 0 | 1 | 2 | 3 |
|---|----|----|----|----|
| 0 | ∞ | 6 | 2 | 8 |
| 1 | 3 | ∞ | 5 | 7 |
| 2 | 9 | 1 | ∞ | 4 |
| 3 | 5 | 3 | 6 | ∞ |
Матрица 3
| | 0 | 1 | 2 | 3 |
|---|----|----|----|----|
| 0 | ∞ | 9 | 1 | 5 |
| 1 | 2 | ∞ | 8 | 6 |
| 2 | 4 | 7 | ∞ | 3 |
| 3 | 3 | 5 | 2 | ∞ |
Матрица 4
| | 0 | 1 | 2 | 3 |
|---|----|----|----|----|
| 0 | ∞ | 8 | 4 | 6 |
| 1 | 5 | ∞ | 3 | 7 |
| 2 | 7 | 2 | ∞ | 1 |
| 3 | 6 | 4 | 5 | ∞ |
Матрица 5
| | 0 | 1 | 2 | 3 |
|---|----|----|----|----|
| 0 | ∞ | 5 | 3 | 4 |
| 1 | 4 | ∞ | 6 | 7 |
| 2 | 2 | 3 | ∞ | 8 |
| 3 | 1 | 6 | 5 | ∞ |
Матрица 6
| | 0 | 1 | 2 | 3 |
|---|----|----|----|----|
| 0 | ∞ | 4 | 8 | 6 |
| 1 | 5 | ∞ | 2 | 9 |
| 2 | 3 | 7 | ∞ | 1 |
| 3 | 6 | 2 | 4 | ∞ |
Матрица 7
| | 0 | 1 | 2 | 3 |
|---|----|----|----|----|
| 0 | ∞ | 1 | 6 | 3 |
| 1 | 4 | ∞ | 5 | 2 |
| 2 | 9 | 3 | ∞ | 7 |
| 3 | 2 | 8 | 4 | ∞ |
Матрица 8
| | 0 | 1 | 2 | 3 |
|---|----|----|----|----|
| 0 | ∞ | 2 | 7 | 5 |
| 1 | 6 | ∞ | 3 | 4 |
| 2 | 1 | 9 | ∞ | 8 |
| 3 | 3 | 6 | 2 | ∞ |
Матрица 9
| | 0 | 1 | 2 | 3 |
|---|----|----|----|----|
| 0 | ∞ | 6 | 4 | 2 |
| 1 | 7 | ∞ | 1 | 3 |
| 2 | 5 | 2 | ∞ | 9 |
| 3 | 8 | 3 | 6 | ∞ |
Матрица 10
| | 0 | 1 | 2 | 3 |
|---|----|----|----|----|
| 0 | ∞ | 3 | 2 | 7 |
| 1 | 6 | ∞ | 5 | 1 |
| 2 | 4 | 9 | ∞ | 8 |
| 3 | 2 | 5 | 3 | ∞ |
Матрица 11
| | 0 | 1 | 2 | 3 |
|---|----|----|----|----|
| 0 | ∞ | 2 | 9 | 1 |
| 1 | 7 | ∞ | 6 | 4 |
| 2 | 5 | 3 | ∞ | 2 |
| 3 | 6 | 8 | 7 | ∞ |
Матрица 12
| | 0 | 1 | 2 | 3 |
|---|----|----|----|----|
| 0 | ∞ | 4 | 6 | 2 |
| 1 | 1 | ∞ | 3 | 5 |
| 2 | 8 | 7 | ∞ | 9 |
| 3 | 2 | 6 | 4 | ∞ |
Матрица 13
| | 0 | 1 | 2 | 3 |
|---|----|----|----|----|
| 0 | ∞ | 5 | 2 | 3 |
| 1 | 6 | ∞ | 4 | 1 |
| 2 | 7 | 3 | ∞ | 8 |
| 3 | 4 | 9 | 6 | ∞ |
Матрица 14
| | 0 | 1 | 2 | 3 |
|---|----|----|----|----|
| 0 | ∞ | 1 | 4 | 6 |
| 1 | 8 | ∞ | 2 | 3 |
| 2 | 5 | 7 | ∞ | 9 |
| 3 | 2 | 3 | 1 | ∞ |
Матрица 15
| | 0 | 1 | 2 | 3 |
|---|----|----|----|----|
| 0 | ∞ | 7 | 8 | 5 |
| 1 | 2 | ∞ | 6 | 3 |
| 2 | 4 | 1 | ∞ | 9 |
| 3 | 3 | 5 | 2 | ∞ |
Реализация#
import math
import copy
class LittleTSPSolver:
def __init__(self, distance_matrix, verbose=False):
"""
distance_matrix: квадратная матрица расстояний (список списков)
verbose: если True, выводит подробные шаги редукции
"""
self.N = len(distance_matrix)
self.orig_matrix = [[float(d) for d in row] for row in distance_matrix]
self.best_cost = float('inf')
self.best_path = []
self.inf = float('inf')
self.verbose = verbose
def solve(self):
# Инициализация отображения индексов
row_idx = list(range(self.N))
col_idx = list(range(self.N))
# Запуск ветвления
self._branch(
matrix=copy.deepcopy(self.orig_matrix),
row_idx=row_idx,
col_idx=col_idx,
path=[],
lower_bound=0.0
)
return self.best_path, self.best_cost
def _branch(self, matrix, row_idx, col_idx, path, lower_bound):
n = len(matrix)
# Базовый случай: осталась одна вершина
if n == 1:
i, j = 0, 0
final_path = path + [(row_idx[i], col_idx[j])]
total_cost = lower_bound + matrix[i][j]
if total_cost < self.best_cost:
self.best_cost = total_cost
self.best_path = final_path
return
# Шаг 1: редукция матрицы и обновление нижней границы
if self.verbose:
print(f"\n--- Редукция на глубине {len(path)} ---")
print("Матрица до редукции:")
self._print_matrix(matrix)
reduction_cost = self._reduce_matrix(matrix)
new_lower = lower_bound + reduction_cost
if self.verbose:
print(f"Стоимость редукции = {reduction_cost}")
print("Матрица после редукции:")
self._print_matrix(matrix)
print(f"Обновленная нижняя граница = {new_lower}\n")
if new_lower >= self.best_cost:
if self.verbose:
print("Обрезка ветви: нижняя граница превышает текущий лучший результат")
return
# Шаг 2: вычисление штрафов для нулей
max_penalty = -1
zero_positions = []
penalties = []
for i in range(n):
for j in range(n):
if matrix[i][j] == 0:
pen = self._compute_penalty(matrix, i, j)
zero_positions.append((i, j))
penalties.append(pen)
if pen > max_penalty:
max_penalty = pen
best_zeros = [pos for pos, pen in zip(zero_positions, penalties) if pen == max_penalty]
i0, j0 = best_zeros[0]
if self.verbose:
print(f"Выбрано нулевое в ({i0},{j0}) с максимальным штрафом {max_penalty}")
# Ветвь 1: включить ребро (i0, j0)
mat1 = copy.deepcopy(matrix)
ridx1 = row_idx.copy()
cidx1 = col_idx.copy()
selected_src = ridx1.pop(i0)
selected_dst = cidx1.pop(j0)
new_path = path + [(selected_src, selected_dst)]
if self.verbose:
print(f"Включить ребро: {selected_src}->{selected_dst}")
self._remove_row_col(mat1, i0, j0)
# запрет обратного ребра
if selected_dst in ridx1 and selected_src in cidx1:
ii = ridx1.index(selected_dst)
jj = cidx1.index(selected_src)
mat1[ii][jj] = self.inf
if self.verbose:
print(f"Убрать обратное ребро: {selected_dst}->{selected_src}")
self._branch(mat1, ridx1, cidx1, new_path, new_lower)
# Ветвь 2: исключить ребро
mat2 = copy.deepcopy(matrix)
ridx2 = row_idx.copy()
cidx2 = col_idx.copy()
if self.verbose:
print(f"Исключить ребро: {row_idx[i0]}->{col_idx[j0]}")
mat2[i0][j0] = self.inf
self._branch(mat2, ridx2, cidx2, path, new_lower)
def _reduce_matrix(self, matrix):
n = len(matrix)
cost = 0.0
# Редукция по строкам
for i in range(n):
row_min = min(matrix[i])
if 0 < row_min < self.inf:
cost += row_min
if self.verbose:
print(f"Минимум в строке {i} = {row_min}")
for j in range(n):
if matrix[i][j] < self.inf:
matrix[i][j] -= row_min
# Редукция по столбцам
for j in range(n):
col_vals = [matrix[i][j] for i in range(n)]
col_min = min(col_vals)
if 0 < col_min < self.inf:
cost += col_min
if self.verbose:
print(f"Минимум в столбце {j} = {col_min}")
for i in range(n):
if matrix[i][j] < self.inf:
matrix[i][j] -= col_min
return cost
def _compute_penalty(self, matrix, r, c):
n = len(matrix)
row_vals = [matrix[r][j] for j in range(n) if j != c]
rmin = min(row_vals) if row_vals else self.inf
col_vals = [matrix[i][c] for i in range(n) if i != r]
cmin = min(col_vals) if col_vals else self.inf
return (rmin if rmin < self.inf else 0) + (cmin if cmin < self.inf else 0)
def _remove_row_col(self, matrix, row, col):
matrix.pop(row)
for r in matrix:
r.pop(col)
def _print_matrix(self, matrix):
for row in matrix:
print(["∞" if val == self.inf else round(val, 2) for val in row])
if __name__ == '__main__':
dist = [
[math.inf, 20, 18, 12, 8],
[5, math.inf, 14, 7, 11],
[12, 18, math.inf, 6, 11],
[11, 17, 11, math.inf, 12],
[5, 5, 5, 5, math.inf]
]
solver = LittleTSPSolver(dist, verbose=True)
path, cost = solver.solve()
print('Best path:', path)
print('Cost:', cost)
#include <iostream>
#include <vector>
#include <limits>
#include <algorithm>
#include <iomanip>
class LittleTSPSolver {
public:
LittleTSPSolver(const std::vector<std::vector<double>>& distance_matrix, bool verbose = false)
: N(distance_matrix.size()), orig_matrix(distance_matrix), best_cost(std::numeric_limits<double>::infinity()),
inf(std::numeric_limits<double>::infinity()), verbose(verbose) {}
std::pair<std::vector<std::pair<int, int>>, double> solve() {
std::vector<int> row_idx(N);
std::vector<int> col_idx(N);
for (int i = 0; i < N; ++i) {
row_idx[i] = i;
col_idx[i] = i;
}
branch(orig_matrix, row_idx, col_idx, {}, 0.0);
return {best_path, best_cost};
}
private:
int N;
std::vector<std::vector<double>> orig_matrix;
double best_cost;
std::vector<std::pair<int, int>> best_path;
double inf;
bool verbose;
void branch(std::vector<std::vector<double>> matrix, std::vector<int> row_idx, std::vector<int> col_idx,
std::vector<std::pair<int, int>> path, double lower_bound) {
int n = matrix.size();
if (n == 1) {
int i = 0, j = 0;
std::vector<std::pair<int, int>> final_path = path;
final_path.emplace_back(row_idx[i], col_idx[j]);
double total_cost = lower_bound + matrix[i][j];
if (total_cost < best_cost) {
best_cost = total_cost;
best_path = final_path;
}
return;
}
if (verbose) {
std::cout << "\n--- Reduction at depth " << path.size() << " ---" << std::endl;
std::cout << "Matrix before reduction:" << std::endl;
print_matrix(matrix);
}
double reduction_cost = reduce_matrix(matrix);
double new_lower = lower_bound + reduction_cost;
if (verbose) {
std::cout << "Reduction cost = " << reduction_cost << std::endl;
std::cout << "Matrix after reduction:" << std::endl;
print_matrix(matrix);
std::cout << "Updated lower bound = " << new_lower << std::endl;
}
if (new_lower >= best_cost) {
if (verbose) {
std::cout << "Pruning branch: lower bound exceeds current best result" << std::endl;
}
return;
}
double max_penalty = -1;
std::vector<std::pair<int, int>> zero_positions;
std::vector<double> penalties;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
if (matrix[i][j] == 0) {
double pen = compute_penalty(matrix, i, j);
zero_positions.emplace_back(i, j);
penalties.push_back(pen);
if (pen > max_penalty) {
max_penalty = pen;
}
}
}
}
std::vector<std::pair<int, int>> best_zeros;
for (size_t k = 0; k < zero_positions.size(); ++k) {
if (penalties[k] == max_penalty) {
best_zeros.push_back(zero_positions[k]);
}
}
int i0 = best_zeros[0].first;
int j0 = best_zeros[0].second;
if (verbose) {
std::cout << "Chosen zero at (" << i0 << "," << j0 << ") with max penalty " << max_penalty << std::endl;
}
// Branch 1: Include edge (i0, j0)
std::vector<std::vector<double>> mat1 = matrix;
std::vector<int> ridx1 = row_idx;
std::vector<int> cidx1 = col_idx;
int selected_src = ridx1[i0];
int selected_dst = cidx1[j0];
ridx1.erase(ridx1.begin() + i0);
cidx1.erase(cidx1.begin() + j0);
std::vector<std::pair<int, int>> new_path = path;
new_path.emplace_back(selected_src, selected_dst);
if (verbose) {
std::cout << "Include edge: " << selected_src << "->" << selected_dst << std::endl;
}
remove_row_col(mat1, i0, j0);
if (std::find(ridx1.begin(), ridx1.end(), selected_dst) != ridx1.end() &&
std::find(cidx1.begin(), cidx1.end(), selected_src) != cidx1.end()) {
int ii = std::distance(ridx1.begin(), std::find(ridx1.begin(), ridx1.end(), selected_dst));
int jj = std::distance(cidx1.begin(), std::find(cidx1.begin(), cidx1.end(), selected_src));
mat1[ii][jj] = inf;
if (verbose) {
std::cout << "Remove reverse edge: " << selected_dst << "->" << selected_src << std::endl;
}
}
branch(mat1, ridx1, cidx1, new_path, new_lower);
// Branch 2: Exclude edge
std::vector<std::vector<double>> mat2 = matrix;
std::vector<int> ridx2 = row_idx;
std::vector<int> cidx2 = col_idx;
if (verbose) {
std::cout << "Exclude edge: " << row_idx[i0] << "->" << col_idx[j0] << std::endl;
}
mat2[i0][j0] = inf;
branch(mat2, ridx2, cidx2, path, new_lower);
}
double reduce_matrix(std::vector<std::vector<double>>& matrix) {
int n = matrix.size();
double cost = 0.0;
for (int i = 0; i < n; ++i) {
double row_min = *std::min_element(matrix[i].begin(), matrix[i].end());
if (0 < row_min && row_min < inf) {
cost += row_min;
if (verbose) {
std::cout << "Minimum in row " << i << " = " << row_min << std::endl;
}
for (int j = 0; j < n; ++j) {
if (matrix[i][j] < inf) {
matrix[i][j] -= row_min;
}
}
}
}
for (int j = 0; j < n; ++j) {
std::vector<double> col_vals(n);
for (int i = 0; i < n; ++i) {
col_vals[i] = matrix[i][j];
}
double col_min = *std::min_element(col_vals.begin(), col_vals.end());
if (0 < col_min && col_min < inf) {
cost += col_min;
if (verbose) {
std::cout << "Minimum in column " << j << " = " << col_min << std::endl;
}
for (int i = 0; i < n; ++i) {
if (matrix[i][j] < inf) {
matrix[i][j] -= col_min;
}
}
}
}
return cost;
}
double compute_penalty(const std::vector<std::vector<double>>& matrix, int r, int c) {
int n = matrix.size();
std::vector<double> row_vals;
for (int j = 0; j < n; ++j) {
if (j != c) {
row_vals.push_back(matrix[r][j]);
}
}
double rmin = row_vals.empty() ? inf : *std::min_element(row_vals.begin(), row_vals.end());
std::vector<double> col_vals;
for (int i = 0; i < n; ++i) {
if (i != r) {
col_vals.push_back(matrix[i][c]);
}
}
double cmin = col_vals.empty() ? inf : *std::min_element(col_vals.begin(), col_vals.end());
return (rmin < inf ? rmin : 0) + (cmin < inf ? cmin : 0);
}
void remove_row_col(std::vector<std::vector<double>>& matrix, int row, int col) {
matrix.erase(matrix.begin() + row);
for (auto& r : matrix) {
r.erase(r.begin() + col);
}
}
void print_matrix(const std::vector<std::vector<double>>& matrix) {
for (const auto& row : matrix) {
for (double val : row) {
if (val == inf) {
std::cout << "∞\t";
} else {
std::cout << std::fixed << std::setprecision(2) << val << "\t";
}
}
std::cout << std::endl;
}
}
};
int main() {
std::vector<std::vector<double>> dist = {
{std::numeric_limits<double>::infinity(), 20, 18, 12, 8},
{5, std::numeric_limits<double>::infinity(), 14, 7, 11},
{12, 18, std::numeric_limits<double>::infinity(), 6, 11},
{11, 17, 11, std::numeric_limits<double>::infinity(), 12},
{5, 5, 5, 5, std::numeric_limits<double>::infinity()}
};
LittleTSPSolver solver(dist, true);
auto [path, cost] = solver.solve();
std::cout << "Best path: ";
for (const auto& edge : path) {
std::cout << "(" << edge.first << "->" << edge.second << ") ";
}
std::cout << "\nCost: " << cost << std::endl;
return 0;
}
Эвристические алгоритмы#
Эвристический алгоритм — это алгоритм решения задачи, правильность которого для всех возможных случаев не доказана, но про который известно, что он даёт достаточно хорошее решение в большинстве случаев.
Эвристические алгоритмы обычно применяются при решении плохо формализованных или сложных задач.
Алгоритм имитации отжига#
Алгоритм имитации отжига (англ. simulated annealing) — эвристический алгоритм глобальной оптимизации, особенно эффективный при решении дискретных и комбинаторных задач.
Алгоритм вдохновлён процессом отжига в металлургии — техники, заключающейся в нагревании и постепенном охлаждении металла для увеличения его кристаллизованности и уменьшения дефектов.
Симулирование отжига в переборных задачах может быть использовано для приближённого нахождения глобального минимума функций с большим количеством свободных переменных.
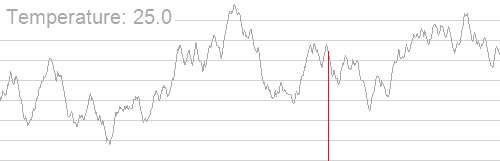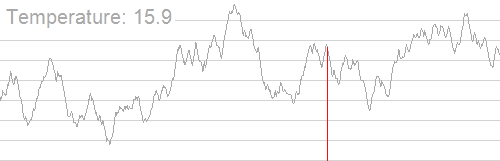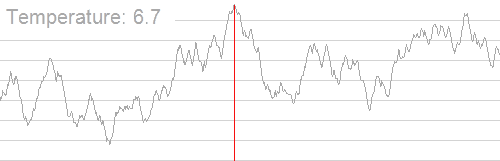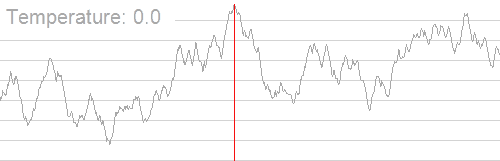
Алгоритм вероятностный и не даёт почти никаких гарантий сходимости, однако хорошо работает на практике при решении NP-полных задач. Иногда на контестах им удаётся сдать сложные комбинаторные задачи, у которых есть нормальное решение.
Рассужджения о методе#
Как и всё гениальное, данный метод подсмотрен у матушки природы. За основу взят процесс кристаллизации вещества, который, в свою очередь, «приручили» хитрые металлурги для повышения однородности металла.
Напомню, что у каждого металла есть кристаллическая решетка — если совсем коротко, она описывает геометрическое положение атомов вещества. Совокупность позиций всех атомов будем называть состоянием системы, каждому состоянию соответствует определённый уровень энергии. Цель отжига – привести систему в состояние с наименьшей энергией. Чем ниже уровень энергии, тем «лучше» кристаллическая решетка, т.е. тем меньше у нее дефектов и прочнее металл.
В ходе «отжига» металл сначала нагревают до некоторой температуры, что заставляет атомы кристаллической решетки покинуть свои позиции. Затем начинается медленное и контролируемое охлаждение. Атомы стремятся попасть в состояние с меньшей энергией, однако, с определённой вероятностью они могут перейти и в состояние с большей. Эта вероятность уменьшается вместе с температурой. Переход в худшее состояние, как ни странно, помогает в итоге отыскать состояние с энергией меньшей, чем начальная. Процесс завершается, когда температура падает до заранее заданного значения.
Как видите, в рамках данного процесса происходит минимизация энергии. Меняем энергию на нашу целевую функцию, и voilà! Или нет? Давайте задумаемся, а чем же так хорош столь мудрёный процесс? Почему бы нам, например, всегда не переходить в состояния с меньшей энергией?
Примерно так работает имеющий широкое распространение метод градиентного спуска.
На просторах интернета мне удалось отыскать совершенно чудесную картинку, которая как нельзя лучше иллюстрирует все плюсы алгоритма.
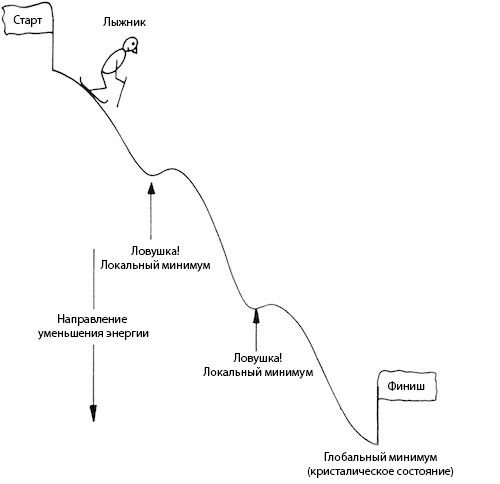
Давайте на минуточку представим себя лыжником, несущемся по крутому склону нашей целевой функции. Задача спуститься в самую нижнюю точку (глобальный минимум). Но, как видите, склон нам попался не совсем ровный, есть на нём низменности, заехав в которые, нам может показаться, что мы уже у подножья. Дабы не остаться в дураках, нам придётся проявить любопытство и вскарабкаться на небольшой холмик, чтобы продолжить спуск.
Чтобы метафора стала окончательно понятна, в примере с лыжником склон – функция измерения энергии вещества (она же целевая функция). А вероятностный переход в состояние с большей энергией – карабканье на холм справа от низменности.
Как видите, такой алгоритм позволяет нам с большой вероятностью избежать «застревания» в локальном минимуме.
Общее описание алгоритма и Пример: задачи коммивояжёра#
Для конкретного примера будем рассматривать задачу коммивояжёра:
Есть n городов, соединённых между собой дорогами. Необходимо проложить между ними кратчайший замкнутый маршрут, проходящий через каждый город только один раз.
Пусть имеется некоторая функция f(x) от состояния x, которую требуется минимизировать. В рассматриваемом случае x — это перестановка вершин (городов) в том порядке, в котором они будут посещаться, а f(x) — длина соответствующего маршрута.
В качестве базового решения выбирается некоторое состояние x₀. В данной задаче удобно взять случайную перестановку как изначальный маршрут. Вводится температура t — положительное действительное число, изначально равное единице, которая будет изменяться по мере оптимизации и определять вероятность перехода в соседнее состояние.
Алгоритм выполняется до тех пор, пока не будет достигнуто оптимальное решение или не закончится отведённое время. На каждой итерации температура уменьшается по некоторой функции T, например, tₖ = T(tₖ₋₁). Затем выбирается случайное соседнее состояние y, получаемое из текущего x небольшим изменением — например, перестановкой двух случайных элементов.
С вероятностью p(f(x), f(y), tₖ) происходит переход к состоянию y, то есть присваивается x ← y, иначе текущее состояние сохраняется. Если y не хуже, то есть f(y) ≤ f(x), переход выполняется всегда. В противном случае используется вероятностный критерий: переход осуществляется с вероятностью p = exp((f(x) - f(y)) / tₖ), где экспонента от отрицательного числа даёт значение в интервале (0, 1). Таким образом, чем хуже новое состояние и чем ниже температура, тем меньше вероятность его принятия.

Интуитивная идея состоит в том, что в начале оптимизации, когда решение далеко от оптимального, допускается больше случайных переходов, в том числе ухудшающих, чтобы избежать попадания в локальные минимумы. В конце, когда решение уже близко к хорошему, температура снижается, и алгоритм работает более «осмотрительно», уточняя результат. Хорошей эвристикой считается правило tₖ = γ ⋅ tₖ₋₁, где γ — число, близкое к единице (например, 0.99). Значение γ подбирается в зависимости от предполагаемого количества итераций: при слишком низкой температуре изменения состояния почти не происходят.
Эффективность метода повышается, если функция f(x) изменяется плавно при небольших изменениях x, то есть является относительно гладкой. Однако важно понимать, что выбор конкретных эвристик не универсален: все составляющие алгоритма сильно зависят от характера задачи и подбираются экспериментально.
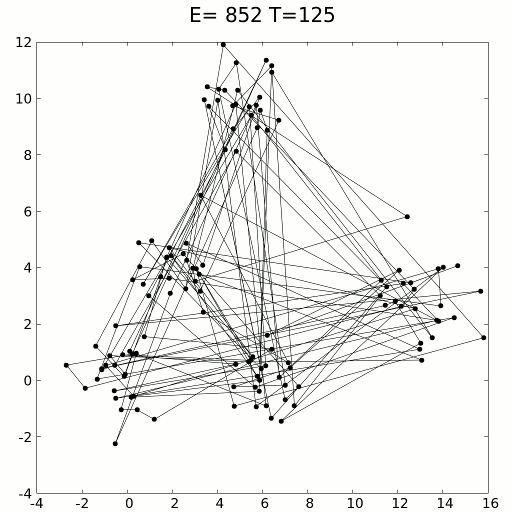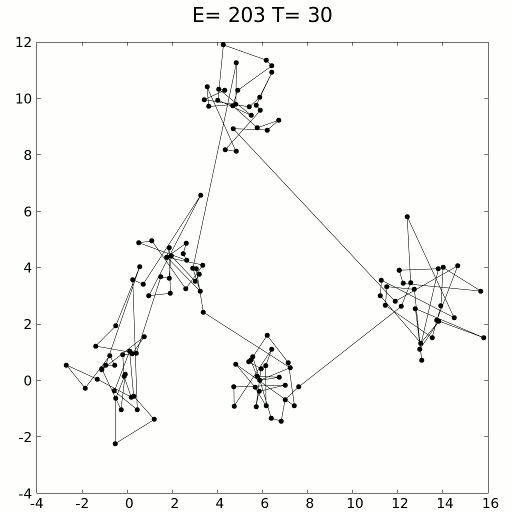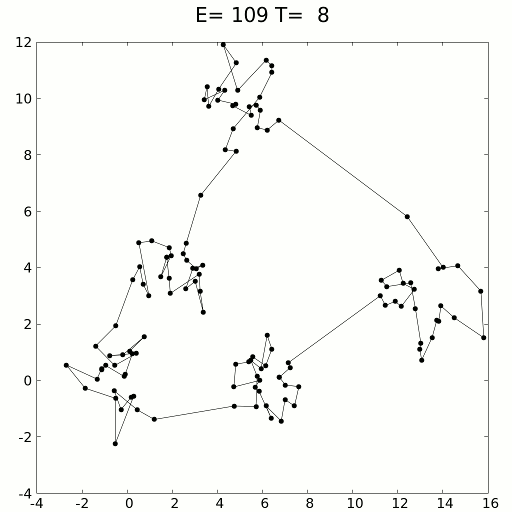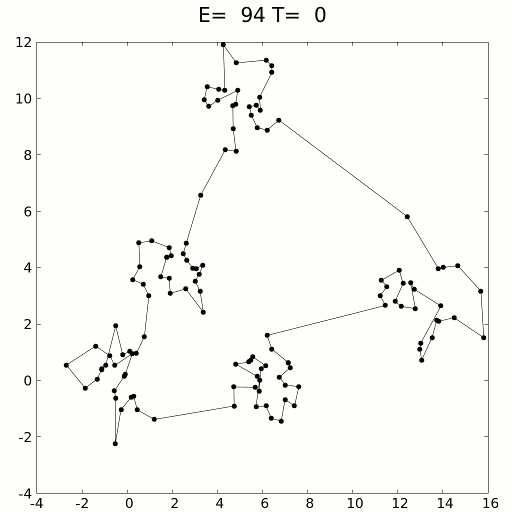
Кодовая реализация#
Это итеративный алгоритм, который очень часто способен найти действительно неплохое решение. Причем, в отличие от жадных алгоритмов, отжиг специально сделан так, чтобы не “застревать” в каких-то локально-хороших точках пространства решений, а наоборот, искать самое лучшее.
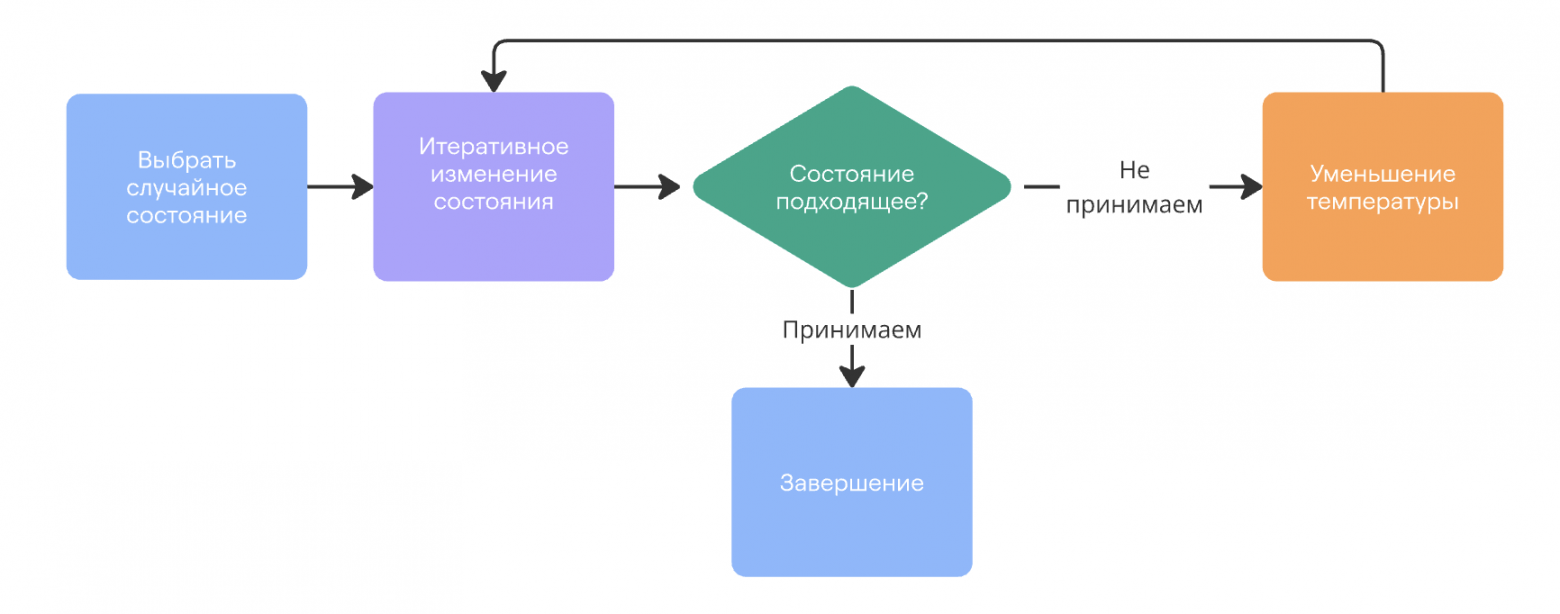
Еще раз повторим суть процесса отжига заключается в следующем:
- Генерируем начальное случайное решение (или получаем feasible при помощи эвристик);
- Задаем начальную “температуру” – некий глобальный метапараметр, суть которого станет ясна далее;
- Выполняем отжиг заданное число итераций;
- Выполняем случайную модификацию решения;
- Если значение функции стоимости для нового решения лучше, чем для старого, то принимаем его;
- Если нет, то все равно можем принять новое решение, но лишь с некоторой вероятностью, которая тем больше, чем выше температура и чем ближе друг к другу по оценке старое и новое решение.
Давайте реализуем это. В качестве функции, которая дает нам вероятность принять/отклонить новое решение, будем использовать распределение Больцмана:
Видно, что эта величина может быть больше единицы в случае, когда новое решение лучше старого, но для нас это не проблема – это просто будет значить, что мы точно принимаем новое решение!
import random
import math
import time
# Матрица расстояний
dist = [
[math.inf, 20, 18, 12, 8],
[5, math.inf, 14, 7, 11],
[12, 18, math.inf, 6, 11],
[11, 17, 11, math.inf, 12],
[5, 5, 5, 5, math.inf]
]
# Функция для подсчета стоимости пути
def compute_way_cost(matrix, way):
"""Функция для подсчета стоимости пути по матрице расстояний."""
cost = 0
for i in range(len(way) - 1):
cost += matrix[way[i]][way[i + 1]]
cost += matrix[way[-1]][way[0]] # Замкнутый путь
return cost
# Функция для генерации нового пути (перестановка двух вершин)
def get_new_way(current_way):
"""Генерация нового пути с помощью случайного обмена двух вершин."""
new_way = current_way.copy()
i, j = random.sample(range(len(current_way)), 2)
new_way[i], new_way[j] = new_way[j], new_way[i]
return new_way
# Оптимизированная версия метода отжига для задачи коммивожера
def simulated_annealing_optimized(matrix=None, t_0=100.0, t_min=0.005):
if matrix is None:
raise ValueError("Matrix cannot be None.")
length = len(matrix)
template = list(range(length))
global_min_cost = float('inf')
random.shuffle(template)
global_min_way = template
current_way = template
current_way_cost = compute_way_cost(matrix, template)
t_k = t_0
k = 1
# Основной цикл отжига
while t_k > t_min:
t_k = t_0 / (1 + k) # Плавное охлаждение температуры
k += 1
# Генерация нового пути и его стоимости
new_way = get_new_way(current_way)
new_cost = compute_way_cost(matrix, new_way)
# Вычисление изменения стоимости
dcost = new_cost - current_way_cost
# Если новый путь лучше или принят с вероятностью
if dcost <= 0 or random.random() < math.exp(-dcost / t_k):
current_way = new_way
current_way_cost = new_cost
# Обновление глобального минимума
if current_way_cost < global_min_cost:
global_min_cost = current_way_cost
global_min_way = current_way
return global_min_way, global_min_cost, k, matrix
# Запуск оптимизированной версии
best_path_optimized, best_cost_optimized, iterations_optimized, matrix_optimized = simulated_annealing_optimized(dist, t_0=100.0, t_min=0.005)
print("Наиболее оптимальный путь:", best_path_optimized)
print("Стоимость пути:", best_cost_optimized)
print("Количество итераций:", iterations_optimized)
#include <iostream>
#include <vector>
#include <cmath>
#include <cstdlib>
#include <ctime>
#include <algorithm>
#include <random>
#include <limits>
#include <tuple>
// Функция для вычисления стоимости пути
int computeWayCost(const std::vector<std::vector<int>>& matrix, const std::vector<int>& way) {
int cost = 0;
for (size_t i = 0; i < way.size() - 1; ++i) {
cost += matrix[way[i]][way[i + 1]];
}
cost += matrix[way.back()][way[0]]; // Замкнутый путь
return cost;
}
// Функция для генерации нового пути путем обмена двух вершин
std::vector<int> getNewWay(const std::vector<int>& currentWay) {
std::vector<int> newWay = currentWay;
int i = rand() % newWay.size();
int j = rand() % newWay.size();
std::swap(newWay[i], newWay[j]);
return newWay;
}
// Алгоритм имитации отжига
std::tuple<std::vector<int>, int, int> simulatedAnnealingOptimized(const std::vector<std::vector<int>>& matrix, double t_0 = 100.0, double t_min = 0.005) {
int length = matrix.size();
std::vector<int> templateWay(length);
for (int i = 0; i < length; ++i) {
templateWay[i] = i;
}
double globalMinCost = std::numeric_limits<int>::max();
// Использование std::shuffle с генератором случайных чисел
std::random_device rd;
std::mt19937 g(rd());
std::shuffle(templateWay.begin(), templateWay.end(), g);
std::vector<int> globalMinWay = templateWay;
std::vector<int> currentWay = templateWay;
int currentWayCost = computeWayCost(matrix, templateWay);
double t_k = t_0;
int k = 1;
// Основной цикл отжига
while (t_k > t_min) {
t_k = t_0 / (1 + k); // Постепенное охлаждение
k += 1;
// Генерация нового пути и его стоимости
std::vector<int> newWay = getNewWay(currentWay);
int newCost = computeWayCost(matrix, newWay);
// Вычисление изменения стоимости
int dcost = newCost - currentWayCost;
// Если новый путь лучше или принят с вероятностью
if (dcost <= 0 || (static_cast<double>(rand()) / RAND_MAX) < exp(-dcost / t_k)) {
currentWay = newWay;
currentWayCost = newCost;
}
// Обновление глобального минимума
if (currentWayCost < globalMinCost) {
globalMinCost = currentWayCost;
globalMinWay = currentWay;
}
}
return std::make_tuple(globalMinWay, static_cast<int>(globalMinCost), k);
}
int main() {
srand(static_cast<unsigned>(time(0))); // Инициализация генератора случайных чисел
// Матрица расстояний
std::vector<std::vector<int>> dist = {
{std::numeric_limits<int>::max(), 20, 18, 12, 8},
{5, std::numeric_limits<int>::max(), 14, 7, 11},
{12, 18, std::numeric_limits<int>::max(), 6, 11},
{11, 17, 11, std::numeric_limits<int>::max(), 12},
{5, 5, 5, 5, std::numeric_limits<int>::max()}
};
// Запуск оптимизированной версии
std::vector<int> bestPathOptimized;
int bestCostOptimized;
int iterationsOptimized;
std::tie(bestPathOptimized, bestCostOptimized, iterationsOptimized) = simulatedAnnealingOptimized(dist, 10.0, 0.5);
std::cout << "Наиболее оптимальный путь: ";
for (int city : bestPathOptimized) {
std::cout << city << " ";
}
std::cout << std::endl;
std::cout << "Стоимость пути: " << bestCostOptimized << std::endl;
std::cout << "Количество итераций: " << iterationsOptimized << std::endl;
return 0;
}
Note
Самостоятельно решите задачу о ферзях при помощи алгоритма имитации отжига.
Дана шахматная доска NxN и ферзей. Нужно расставить их так, чтобы они не били друг друга.
Список использованных источников и благодарностей#
1.(Алгоритмика)[https://ru.algorithmica.org/cs/combinatorial-optimization/annealing/]
2.(QMLCourse)[https://quantum-ods.github.io/qmlcourse/book/problems/ru/copt.html#id13]