Практика 12. Задача коммивояжера

Одна из самых известных и важных задач транспортной логистики (и комбинаторной оптимизации) – задача коммивояжера или «задача о странствующем торговце» (англ. «Travelling Salesman Problem», TSP). Также встречается название «задача китайского почтальона» (англ. «Chinese Postman Problem», CPP).

Суть задачи сводится к поиску оптимального (кратчайшего, быстрейшего или самого дешевого) пути, проходящего через промежуточные пункты по одному разу и возвращающегося в исходную точку. К примеру, нахождение наиболее выгодного маршрута, позволяющего коммивояжеру посетить со своим товаром определенные города по одному разу и вернуться обратно.

Мерой выгодности маршрута может быть минимальное время поездки, минимальные расходы на дорогу или минимальная длина пути. В наше время, когда стоимость доставки часто бывает сопоставима со стоимостью самого товара, а скорость доставки — один из главных приоритетов, задача нахождения оптимального маршрута приобретает огромное значение.

Можете предложить, как решить эту задачу?

Формальная постановка задачи

Задача коммивояжера (TSP) заключается в нахождении оптимального пути, который проходит через все города, посещая каждый город один раз и возвращается в исходную точку. Пусть дан граф $G = (V, E)$, где:

• $V = \{v_1, v_2, \dots, v_n\}$ — множество городов,
• $E = \{e_{ij}\}$ — множество рёбер, где $e_{ij}$ — расстояние между городами $v_i$ и $v_j$.

Задача сводится к нахождению минимального пути $C$, который соединяет все города, то есть находит такой цикл, который минимизирует суммарное расстояние:

$$C = \{v_1, v_2, \dots, v_n, v_1\}$$

Задача может быть математически выражена как минимизация функции стоимости пути $f(x)$, где $x$ — последовательность городов:

$$f(x) = \sum_{i=1}^{n-1} d(x_i, x_{i+1}) + d(x_n, x_1)$$

где $d(x_i, x_{i+1})$ — расстояние между городами $x_i$ и $x_{i+1}$.

Цель задачи:

$$\min_{x} f(x)$$

где $x$ — это перестановка всех городов.

Задача коммивояжера является NP-трудной задачей, то есть её решение требует экспоненциального времени для поиска оптимального пути при увеличении количества городов.

Визуализация

Воспользуемся визуализацией Travelling Salesman Problem Visualiser.
Выставим параметры 4 веришины и метод решения BruteForce (полный перебор)

Также вы можете посмотреть этот же алгоритм на примере иной виузалиазции (TSPVIS)[https://tspvis.com/]

Полный перебор

Представьте, что вы торговый представитель, который хочет объехать несколько ближайших городов.

Схематично маршруты между городами можно обозначить так:

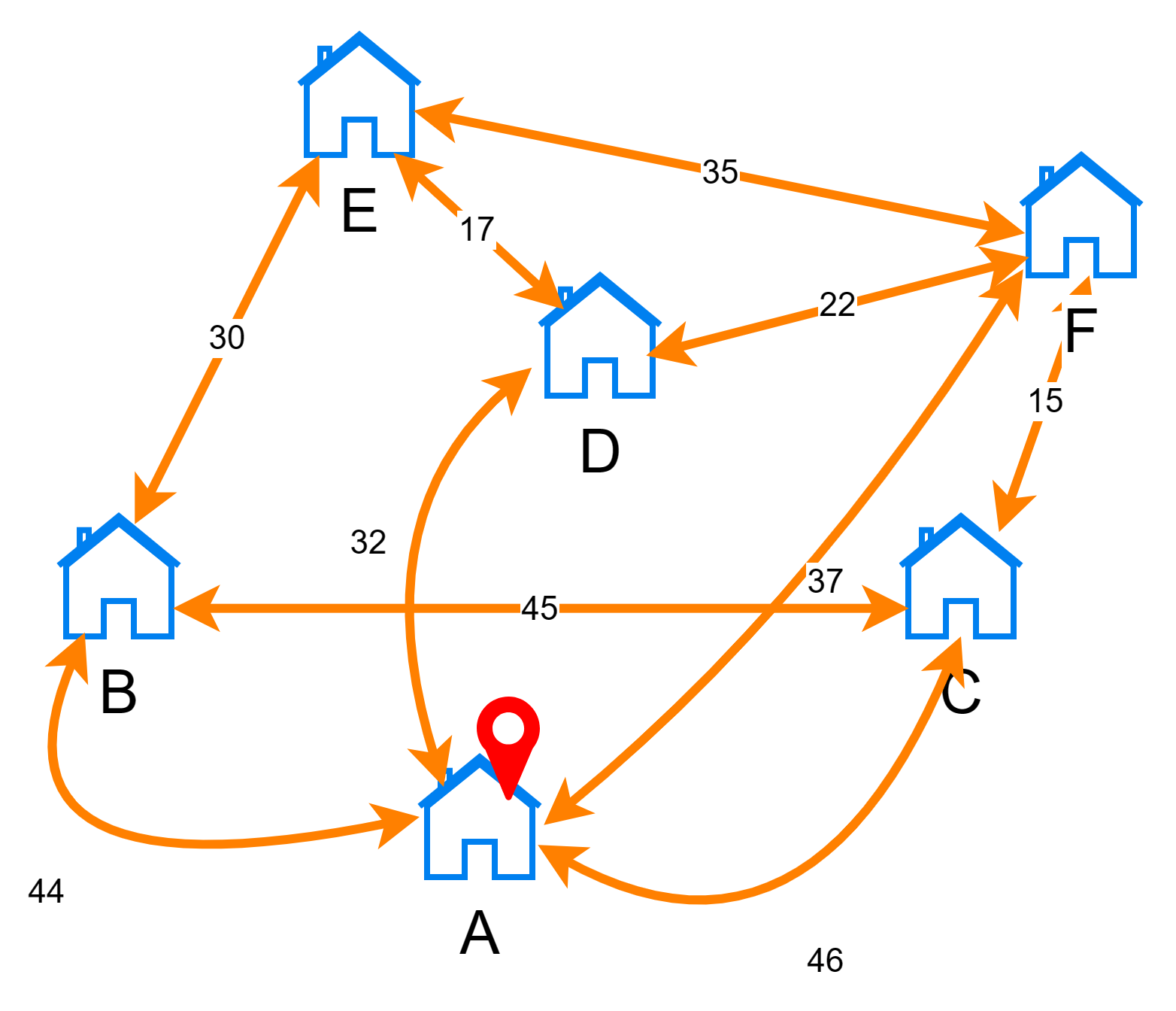
Для начала рассмотрим решение задачи коммивояжера методом полного перебора. Алгоритм заключается в следующем:

1. Построение всех возможных маршрутов.
2. Вычисление веса всех рёбер в каждом маршруте.
3. Нахождение маршрута с минимальной суммой.

Пример

Рассмотрим маршрут по городам A, B, C, F, E, D. Пусть расстояния между городами следующие:

• Из города A в B — 44 километра.
• Из города B в C — 45 километров.
• Из города C в F — 15 километров.
• Из города F в E — 35 километров.
• Из города E в D — 17 километров.
• Из города D в A — 32 километра (чтобы замкнуть маршрут).

Общий маршрут составит:

$$44 + 45 + 15 + 35 + 17 + 32 = 188 \text{ километров}.$$

Затем мы строим другой маршрут и, попутно вычисляя его суммарный вес, находим тот маршрут, который короче текущего. Если новый маршрут короче, то он становится лучшим решением.

После того как алгоритм переберёт все возможные варианты маршрутов, останется лучший найденный маршрут с минимальной суммой.

Пример невозможного маршрута

Однако бывают случаи, когда решение не существует. Например, если граф такой, что невозможно пройти через все вершины, начиная из одной точки и посещая каждую вершину ровно один раз, то метод перебора должен вернуть неудачное решение.

Для примера рассмотрим такой граф:

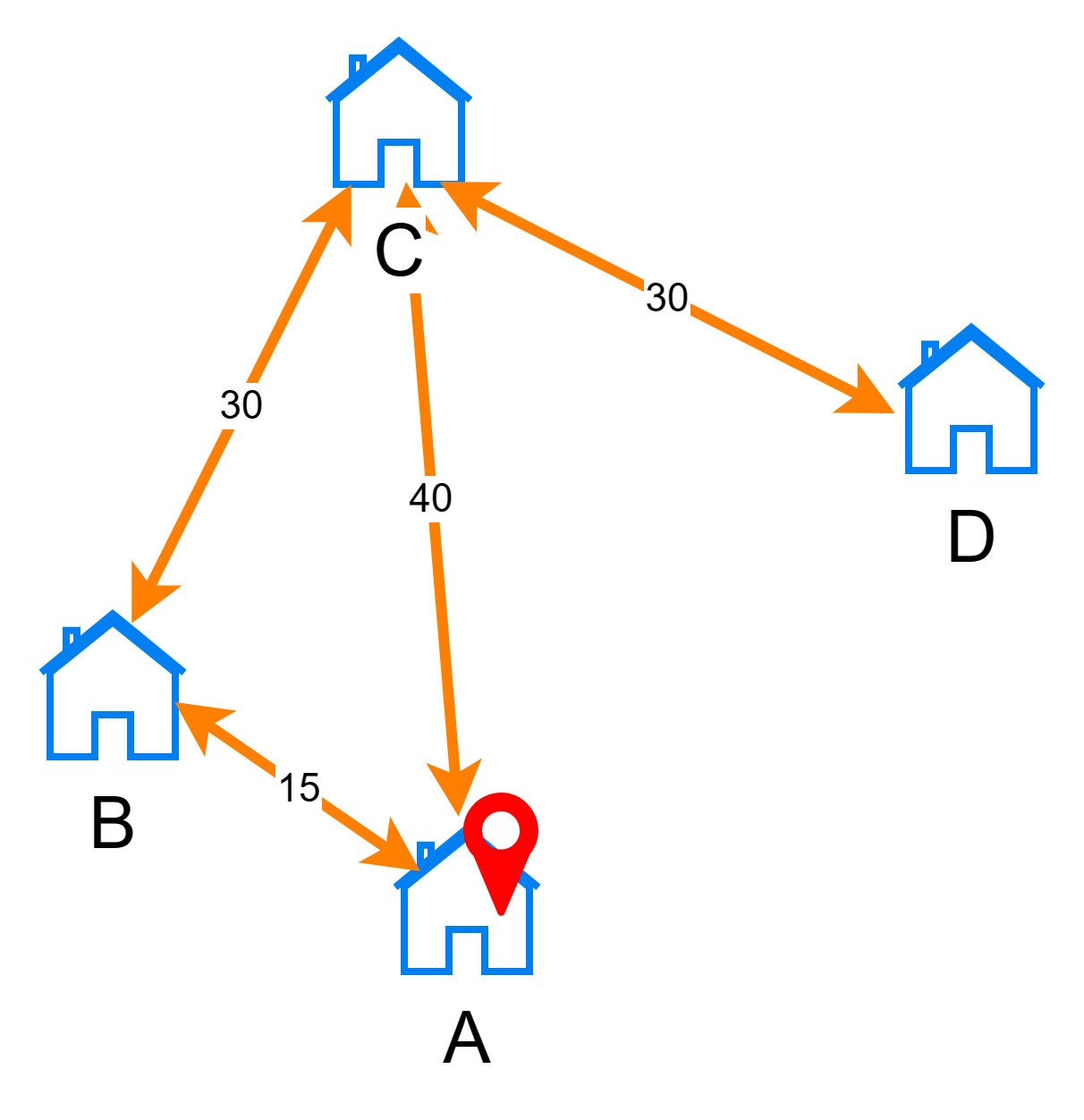
В данном случае метод перебора должен вернуть результат, который обозначает отсутствие решения — например, значение null или пустой массив.

Итог: Метод полного перебора позволяет найти решение задачи коммивояжера, перебирая все возможные маршруты. Однако этот метод может быть неэффективен для больших графов, так как количество возможных маршрутов растет экспоненциально с увеличением числа городов.

Реализуйте полный перебор с использованием алгоритма поиска в глубину для поиска

Ближайший сосед (жадный алгоритм)

Метод ближайшего соседа — это жадный алгоритм для решения задачи коммивояжера, при котором маршрут строится по принципу последовательного выбора ближайшего не посещенного города. Алгоритм очень прост и заключается в следующем:

1. Начинаем с произвольного города (например, первого).
2. Выбираем ближайший город из оставшихся непосещенных и добавляем его в маршрут.
3. Повторяем шаг 2, пока не посетим все города.
4. После того как все города посещены, возвращаемся в начальный город, чтобы замкнуть маршрут.

Важным моментом является то, что на каждом шаге мы выбираем ближайший город (по минимальному расстоянию) к последнему посещенному городу.

Пример

Предположим, у нас есть 4 города: A, B, C и D. Расстояния между городами следующие:

• Расстояние между A и B — 10 км.
• Расстояние между A и C — 15 км.
• Расстояние между A и D — 20 км.
• Расстояние между B и C — 35 км.
• Расстояние между B и D — 25 км.
• Расстояние между C и D — 30 км.

Алгоритм будет работать следующим образом:

1. Начинаем с города A.
2. Выбираем ближайший город к A. Это город B (расстояние 10 км).
3. Теперь в маршруте A → B. Следующий город — ближайший к B, это D (расстояние 25 км).
4. Теперь в маршруте A → B → D. Оставшийся город — C (расстояние 30 км).
5. Закрываем маршрут, возвращаемся из C в A (расстояние 15 км).

Итак, маршрут, построенный методом ближайшего соседа, выглядит как:

A → B → D → C → A.

Общий путь:

$$10 \, \text{км} + 25 \, \text{км} + 30 \, \text{км} + 15 \, \text{км} = 80 \, \text{км}$$

Преимущества метода

• Простота реализации.
• Работает быстро, особенно для небольших чисел городов.

Недостатки

• Алгоритм не гарантирует оптимальный маршрут.
• Может дать подоптимальное решение, особенно при сложных графах.

Метод ветвей и границ

Алгоритмы с факториальной сложностью O(n!) работают даже медленнее алгоритмов с экспоненциальной сложностью O(2^n). Для пяти вершин алгоритм перебрал всего 4!=24 маршрута. Но чем больше вершин, тем сложнее:

Для 10 городов потребуется сравнить больше 300 000 маршрутов
Для 21 города количество вариантов возрастает до миллиарда миллиардов. Если тысяча мощных компьютеров будет перебирать миллион вариантов в секунду, то для решения задачи потребуется чуть больше тридцати лет.
Ранее в курсе мы узнали, что есть способ найти более быстрое решение — жадный алгоритм. К сожалению, он часто оказывается неоптимальным. Обсудим его подробнее.

Вместо перебора, мы можем воспользоваться другим способом — методом ветвей и границ. Перебор выбирает одно единственное решение, которое кажется лучшим. В отличие от него, метод ветвей и границ концентрируется на том, чтобы отбрасывать заведомо плохие варианты.

Как и перебор, метод ветвей и границ гарантирует нахождение лучшего решения, но при этом он может найти его за приемлемое время. Но есть потенциальная проблема — в худшем случае он вырождается в метод перебора и может работать слишком долго.

Как работает метод ветвей и границ

Метод ветвей и границ довольно сложный. Он позволяет решать разные задачи на графах — задачу о рюкзаке, о коммивояжере и другие. Именно поэтому его описание достаточно абстрактное.

Кроме того, сам метод состоит из нескольких шагов. Их детальное описание может отличаться от задачи к задаче.

Чтобы упростить изучение метода, мы освоим его в два этапа. Сейчас рассмотрим метод в целом и применительно к задаче коммивояжера, а уже в следующем уроке — познакомимся с алгоритмом Литтла.

Отличие от метода перебора

И перебор, и метод ветвей и границ обходят деревья решений, но строят эти деревья по-разному. Для примера сравним деревья, которые получаются для графа из четырех вершин.

В методе перебора мы начинаем с пустого графа — графа без построенного маршрута. На первом шаге у нас есть три возможных варианта начать маршрут:

• Ребро 1-2
• Ребро 1-3
• Ребро 1-4

Из корня мы начинаем строить три поддерева, каждое из которых соответствует одному из ребер.

Будем работать с каждым поддеревом по очереди. Сначала обработаем узел, который соответствует ребру 1-2. На этом этапе алгоритм построил маршрут до вершины 2. Далее он может добавить:

• Либо ребро 2-3
• Либо ребро 2-4

Значит, из узла 1-2 можно построить еще два поддерева.

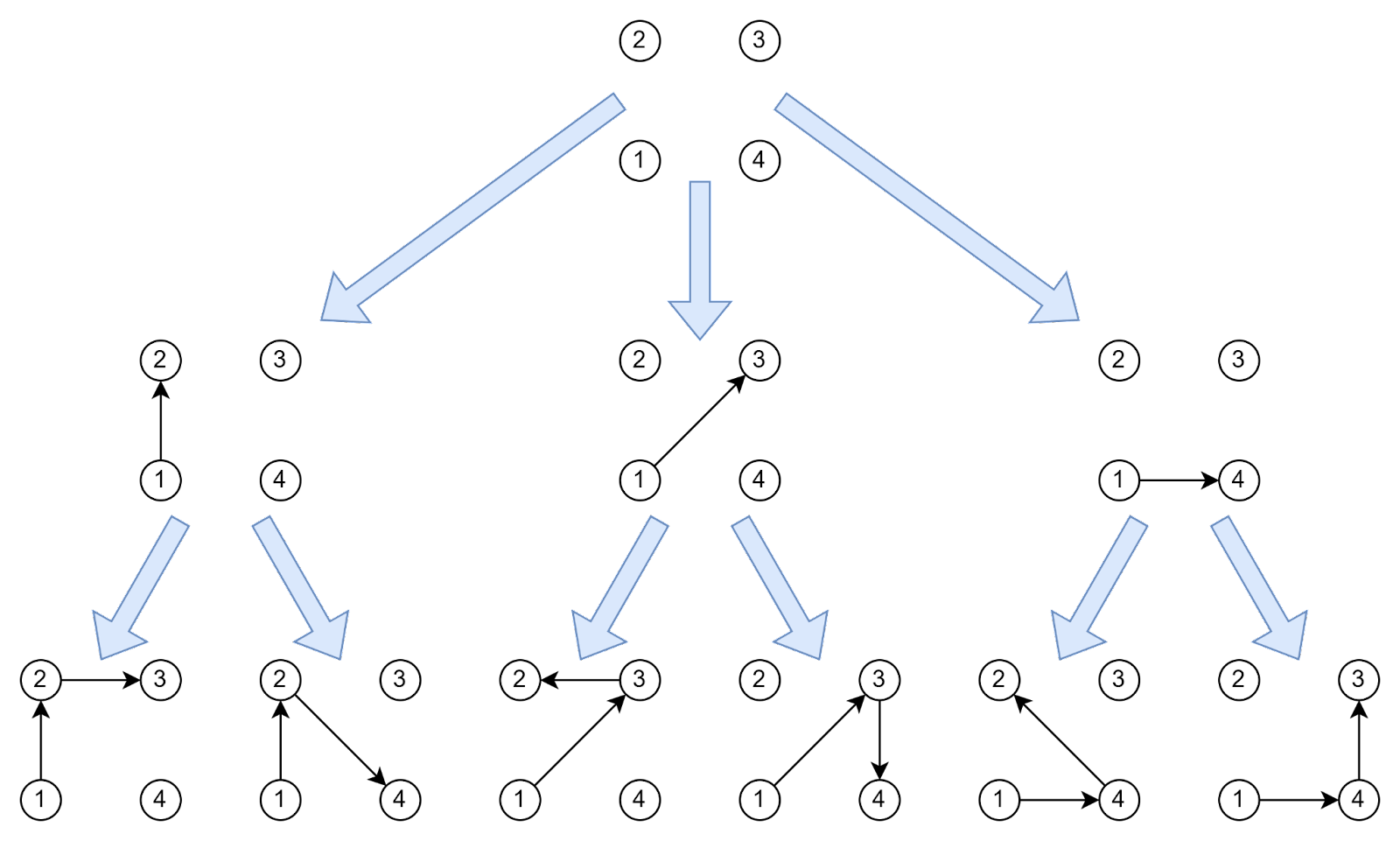
В методе ветвей и границ построение дерева также начинается с пустого графа, но алгоритм всегда строит бинарное дерево.

Он берет первое доступное ребро 1-2 и строит два поддерева:

• В первое попадают те маршруты, где ребро 1-2 есть
• Во второе — те, где его нет

Посмотрим на узел, соответствующий узлу 1-2. Как мы помним, из него выходят два ребра, чтобы продолжить маршрут:

• Ребро 2-3
• Ребро 2-4

Выбираем первый вариант и снова строим два поддерева — с ребром 2-3 и без него.

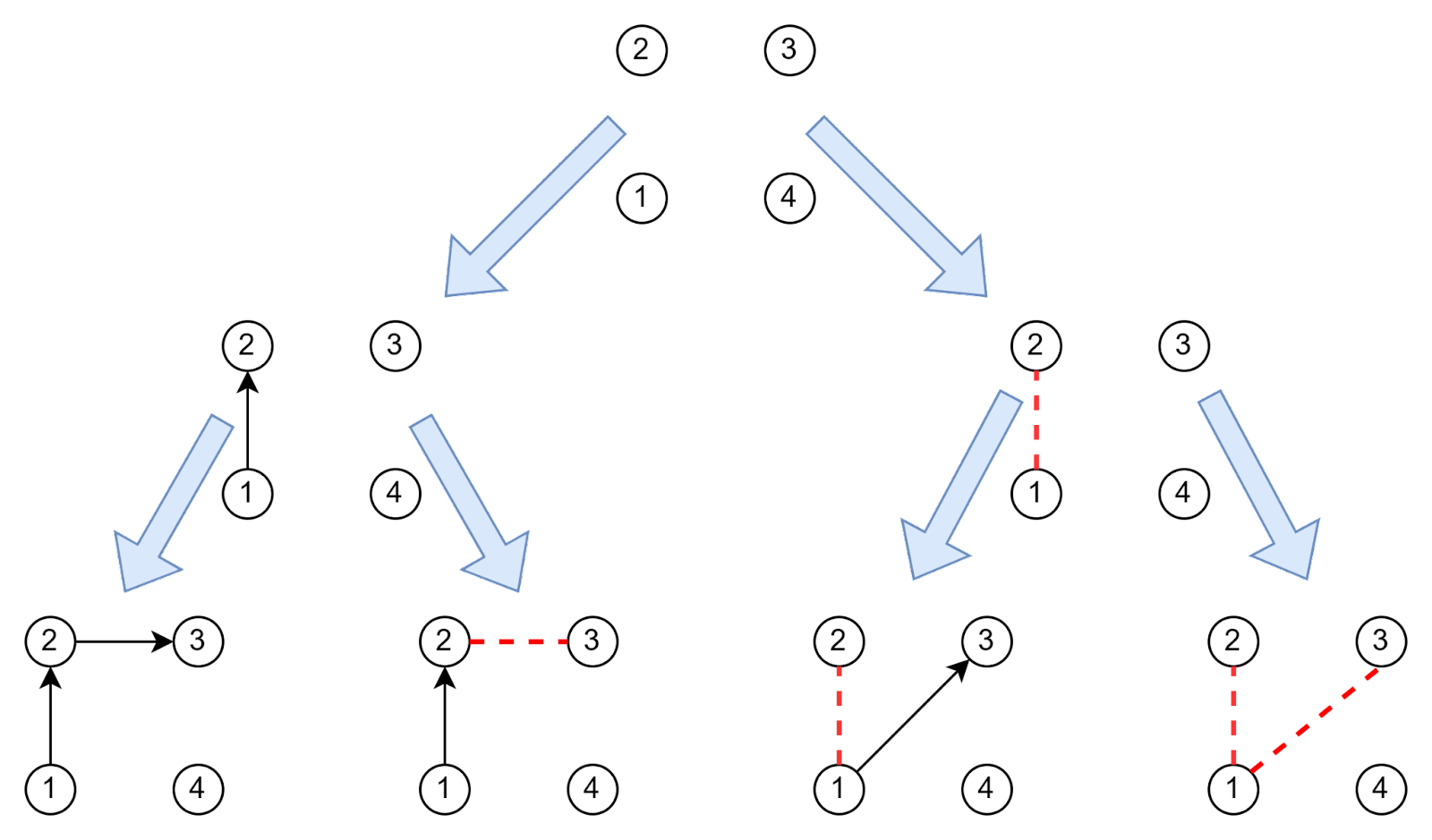
Нижняя граница

Построив очередное поддерево, попытаемся оценить нижнюю границу длины всех маршрутов в этом поддереве.

Это не так просто. Если бы поддерево было построено, мы могли бы найти самый короткий маршрут, сравнив длины всех маршрутов. Но сейчас у нас есть только корень поддерева.

Нижняя граница должна быть совершенно корректна — в поддереве не должно быть маршрутов короче ее. С другой стороны, мы не можем просто использовать ноль, мы хотим оценить нижнюю границу как можно точнее. Таким образом метод ветвей и границ не будет тратить время на заведомо плохие поддеревья.

Мы вернемся к вопросу о том, как оценивать нижнюю границу, разбирая алгоритм Литтла в следующем уроке. Пока же будем считать, что способ оценки нам известен и он достаточно точен.

Отсечение ветвей

Встретив поддерево с большой нижней границей, мы можем отказаться от его обработки, потому что все решения в нем будут слишком длинными. Иными словами, мы можем отсечь эту ветвь дерева решений.

На этом шаге можно случайно отбросить ветвь, которая только выглядит плохой, а на самом деле содержит кратчайший маршрут.

Чтобы этого не допустить, нужно все тщательно проверить. Есть несколько способов убедиться, что в поддереве нет кратчайшего маршрута:

• Сравнить верхние и нижние границы. Представим, что в первом поддереве верхняя граница меньше, чем нижняя граница во втором. В таком случае все маршруты второго поддерева длиннее, чем маршруты первого. Это значит, что второе поддерево можно отсечь, потому что самого короткого маршрута в нем точно нет.
• Построить дерево решений вглубь и добраться до первого завершенного маршрута. Этот маршрут — лучший из тех, что нам известны. В оригинальном описании алгоритма его называют рекордным. Скорее всего, это не самый короткий маршрут. По мере работы алгоритм может найти более короткий путь — тогда он будет рекордным. Если нижняя граница поддерева больше, чем длина рекордного маршрута, это поддерево также можно отсекать.

В алгоритме Литтла применяется второй подход. В следующем уроке мы разберемся с тем, как строить рекордные маршруты.

Рекурсия

После отсечения у нас остаются несколько ветвей, где может находиться оптимальное решение. Мы рекурсивно продолжаем работу с самой перспективной ветвью — это ветвь с наименьшей нижней границей. Для хранения не отсеченных ветвей удобно использовать структуру данных, которая называется очередь с приоритетом. Значения в такую очередь добавляются в произвольном порядке, а извлекаются в порядке возрастания или убывания приоритета.

Рекурсия завершается, когда на очередном шаге мы добираемся до листа в дереве решений.

На рисунке ниже вы увидите пример готового дерева. Мы обрезаем две ветви и добираемся до оптимального решения, в данном случае — до маршрута 1-2-4-3:

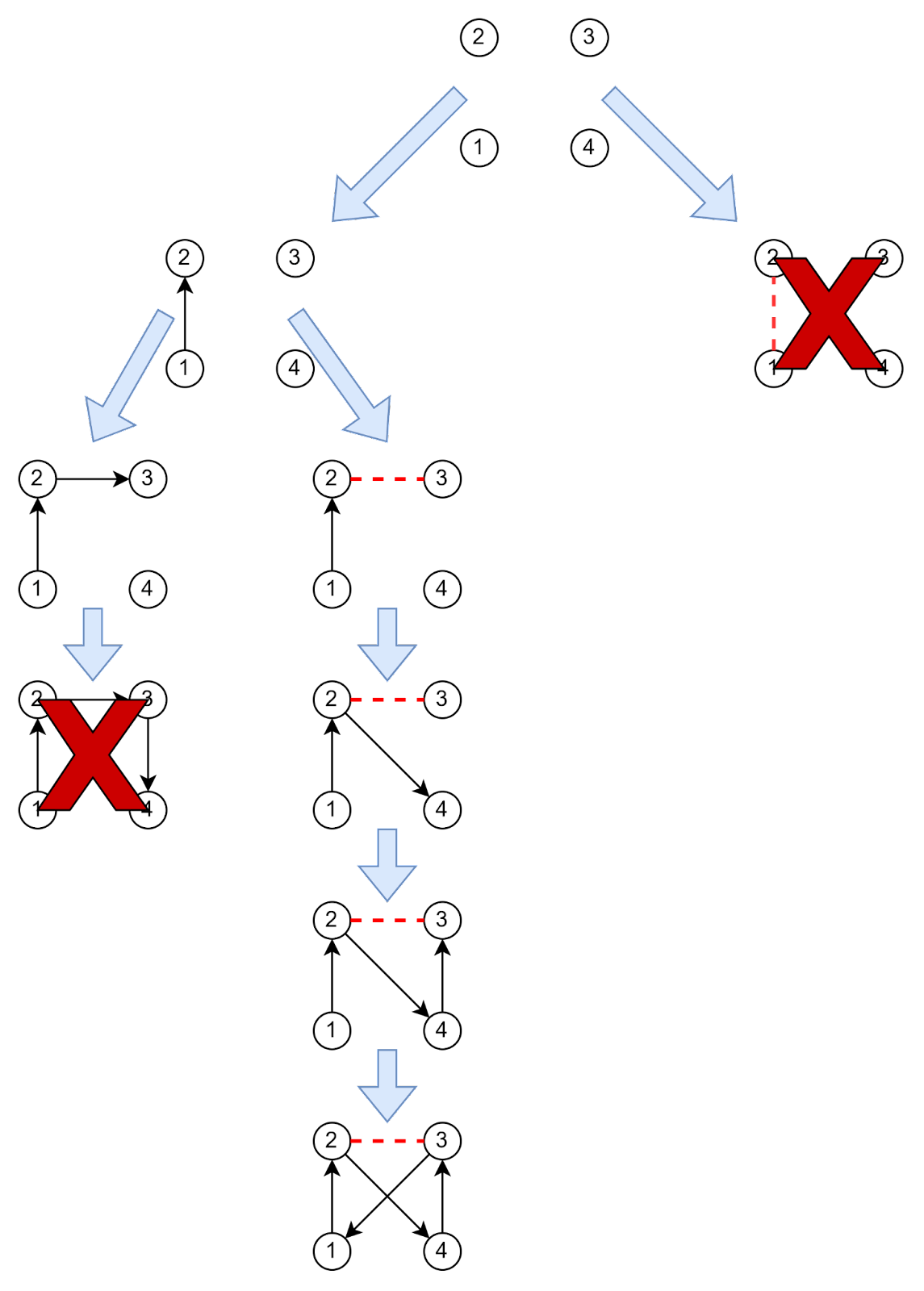
Связанные задачи

Tip

(Муравьиные алгоритмы)[https://blog.bullgare.com/wp-content/uploads/2019/05/aca.pdf]

Список использованных источников и благодарностей

1.(TSPVIS)[https://tspvis.com/]
2.(Travelling Salesman Problem Visualiser!)[https://ellipsoul.github.io/Travelling-Salesman-Visualiser/]
3. (Задача коммивояжера (TSP) точное решение — метод динамического программирования)[https://habr.com/ru/articles/701458/]