Практика 11. Жадные алгоритмы. Алгоритм А*#
Есть много методов решения тех или иных задач: динамическое программирование, перебор. Не менее известными и довольно распространенными являются жадные алгоритмы.
Думаю, каждый программист в своей жизни хотя бы раз написал жадину, может быть, даже не задумываясь об этом. Что же это такое?
Определение жадного алгоритма
Жадными называют класс алгоритмов, заключающихся в принятии локально оптимальных решений на каждом этапе.
К примеру, алгоритм Дейкстры нахождения кратчайшего пути в графе вполне себе жадный, потому что мы на каждом шагу ищем вершину с наименьшим весом, в которой мы еще не бывали, после чего обновляем значения других вершин. При этом можно доказать, что кратчайшие пути, найденные в вершинах, являются оптимальными.
Чтобы это осмыслить рассмотрим задачу о размене монет:
Задача о размене монет
У нас есть набор монет с разными номиналами, и нам нужно разменять заданную сумму минимальным количеством монет.
Предложите решение. Надеюсь, что вы не посмотрите решение раньше, чем подумаете о нем
Размышления о решении#
Решение: используем как можно больше монет с максимальным номиналом, затем переходим к меньшему номиналу и так далее. По крайней мере, так мы можем решать эту задачу в духе жадных алгоритмов.
def coinChange(coins, amount):
coins.sort(reverse=True)
count = 0
for coin in coins:
while amount >= coin:
amount -= coin
count += 1
return count if amount == 0 else -1
coins = [1, 5, 10, 25]
amount = 63
print(coinChange(coins, amount)) # Output: 6 (25 + 25 + 10 + 1 + 1 + 1)
#include <iostream>
#include <vector>
#include <algorithm>
int coinChange(std::vector<int>& coins, int amount) {
std::sort(coins.begin(), coins.end(), std::greater<int>());
int count = 0;
for (int coin : coins) {
while (amount >= coin) {
amount -= coin;
count++;
}
}
return (amount == 0) ? count : -1;
}
int main() {
std::vector<int> coins = {1, 5, 10, 25};
int amount = 63;
int result = coinChange(coins, amount);
std::cout << result << std::endl; // Output: 6 (25 + 25 + 10 + 1 + 1 + 1)
return 0;
}
Функция coinChange получает на вход список монет coins и сумму amount, которую надо разменять. Разберём, что в ней происходит:
- Мы сортируем монеты в порядке убывания, чтобы начать с самых больших монет. В нашем случае это 25, затем 10, 5 и 1.
Создаем переменную count, которая будет считать количество использованных монет. - Идем по списку монет и для каждой монеты, пока можем, вычитаем ее номинал из суммы и увеличиваем счетчик монет count.
Если в итоге сумма стала равна нулю, значит, мы успешно разменяли ее, и тогда возвращаем количество использованных монет — задача решена. Если нет, возвращаем -1, потому что разменять оставшуюся сумму с такими монетами нельзя. - В итоге для набора монет [1, 5, 10, 25] и суммы 63 функция вернёт число 6, потому что нам потребуется 6 монет для размена: две по 25, одна по 10 и три по 1.
Когда жадный алгоритм не сработает? Подберите входные данные. Затем сверьтесь с объяснением
Когда жадный алгоритм не сработает
Пусть у нас есть следующий набор монет: [1, 4, 5]. Теперь допустим, нам нужно разменять сумму 8.
Если мы применим жадный алгоритм к этому набору монет, он сначала выберет монету с номиналом 5, так как она имеет наибольший номинал. Затем, чтобы разменять оставшуюся сумму 3, алгоритм выберет три монеты по 1. В итоге, жадный алгоритм использует 4 монеты: [5, 1, 1, 1].
Однако, оптимальное решение здесь — использовать две монеты по 4 (сумма 8 разменяется на [4, 4]). В этом случае, жадный алгоритм не приводит к оптимальному результату.
Алгоритм А*#
Можно ли себе представить жадную стратегию для задачи поиска кратчайшего пути? Конечно! мы всегда будем выбирать крачайшее ребро из списка и продвигаться вперед.
Алгоритм Дейкстры хорош в поиске кратчайшего пути, но он тратит время на исследование всех направлений, даже бесперспективных. Жадный поиск исследует перспективные направления, но может не найти кратчайший путь. Хочется найти между ними баланс.
Подробное описание#
A* — это модификация алгоритма Дейкстры, оптимизированная для поиска пути к единственной конечной точке.
- Алгоритм Дейкстры ищет кратчайшие пути от начальной вершины ко всем остальным.
- Алгоритм A* фокусируется только на одной цели и использует эвристику, чтобы быстрее к ней прийти.
Представим, что нам необходимо попасть из точки A в точку B. Прямой путь между этими двумя точками разделён стеной, как показано на рисунке 1.
Для упрощения области поиска пути, её необходимо разделить на сетку с квадратными ячейками (смотри рисунок 2). Это позволит выразить область поиска пути через двумерный массив, каждый элемент которого будет представлять одну из клеток получившейся сетки. Одним из значений каждой ячейки массива будет проходимость соответствующей ей клетки (проходима или непроходима).
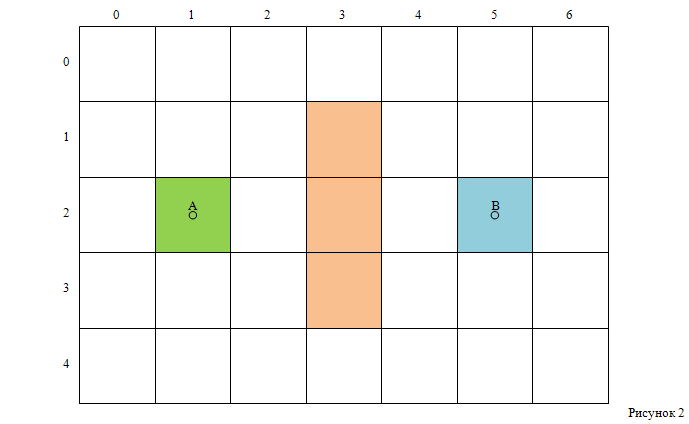
Для нахождения пути необходимо определить, какие именно клетки нужны для перемещения из точки A в точку B. Как только путь будет найден, можно начинать перемещение из центра клетки A в центр следующей клетки пути, до тех пор, пока не будет достигнута конечная точка B.
Замечание: Сетка не обязательно строится из квадратных ячеек. Она может быть построена из прямоугольных ячеек, из шестиугольных ячеек, из треугольных ячеек, или из любых других ячеек.
При этом центральные точки ячеек называют вершинами. Вершины могут располагаться как в центре, так и вдоль граней, или ещё где-нибудь.
Поиск пути начинаем со следующих шагов:
-
Добавляем стартовую клетку, где находится точка A, в «открытый список».
В данный момент в этом списке будет находиться только одна ячейка, но позже в него будут добавляться и другие.
Клетки, находящиеся в открытом списке — это клетки, которые необходимо проверить и решить, будут ли они являться частью искомого пути к конечной клетке. -
Ищем проходимые клетки, граничащие со стартовой клеткой, игнорируя непроходимые клетки (со стенами, водой и прочим),
и добавляем их в открытый список.
Для каждой из этих клеток сохраняем клетку A как «родительскую». -
Удаляем стартовую клетку A с открытого списка и добавляем её в «закрытый список» клеток, которые больше не нужно проверять.
После этих шагов должно получиться нечто похожее на то, что изображено на рисунке 3.
На нём стартовая клетка выделена оранжевым цветом — она находится в закрытом списке.
Все соседние клетки находятся в открытом списке — они выделены синим цветом.
Каждая из этих клеток имеет указатель, направленный на родительскую клетку — стартовую клетку A.
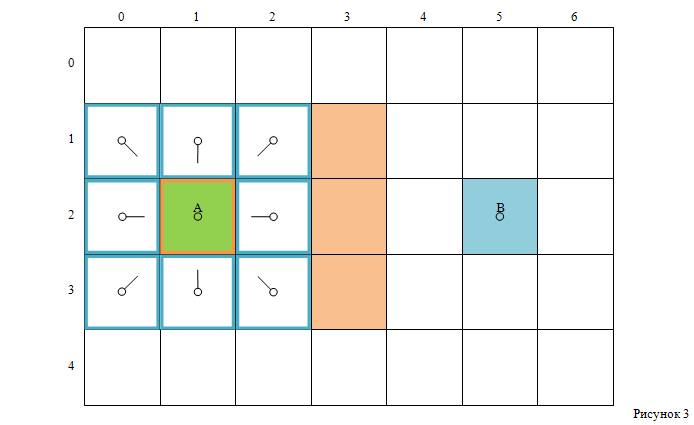
Далее необходимо выбрать одну клетку из находящихся в открытом списке, и, практически, повторить вышеописанный процесс.
Но следующая клетка из открытого списка выбирается не случайно, а в зависимости от её величины F.
Величина F вычисляется по формуле (1):
F = G + H (1)
где:
- G – энергия, затрачиваемая на передвижение из стартовой клетки A в текущую рассматриваемую клетку, следуя найденному пути к этой клетке;
- H – примерное количество энергии, затрачиваемое на передвижение от текущей клетки до целевой клетки B.
Изначально эта величина равна предположительному значению, такому, что если бы мы шли напрямую, игнорируя препятствия (но исключив диагональные перемещения).
В процессе поиска она корректируется в зависимости от встречающихся на пути преград.
Обычно, энергия, затрачиваемая на прохождение в соседнюю клетку по горизонтали, берётся равной 10 единицам,
а по диагонали – 14 единицам.
Для вычисления величины G текущей рассматриваемой клетки,
необходимо величину G её родительской клетки сложить с 10 или 14
(в зависимости от диагонального или ортогонального расположения текущей клетки относительно родительской).
Величина H обычно вычисляется методом Манхэттена.
Суть его заключается в том, чтобы сосчитать общее количество клеток, необходимых для достижения целевой клетки B
от текущей рассматриваемой клетки, причём игнорируя диагональные перемещения и любые препятствия.
Затем полученное количество умножается на 10.
Рассчитав величину F по формуле (1) для всех клеток в открытом списке,
получим результат, похожий на то, что изображено на рисунке 4.
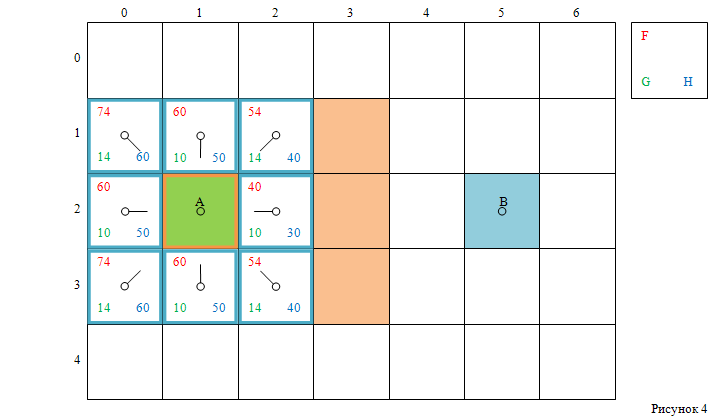
Клетки, расположенные ортогонально к стартовой клетке, имеют значение G, равное 10,
а клетки, расположенные диагонально – G, равное 14.
Значение H равняется Манхэттенскому расстоянию от центра текущей клетки до центра целевой клетки B,
умноженное на 10.
Например, для клетки с индексами [2, 2], расстояние от её центра до центра целевой – 3 клетки (см. рисунок 5).
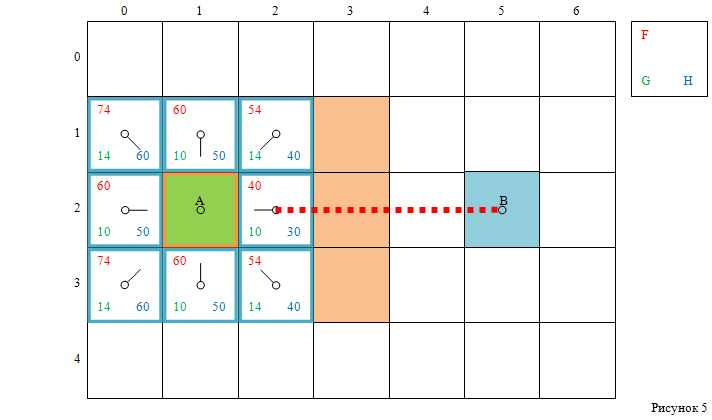
А для клеток с индексами [1, 0] и [3, 0], расстояние до целевой клетки – 6 клеток (см. рисунок 6).
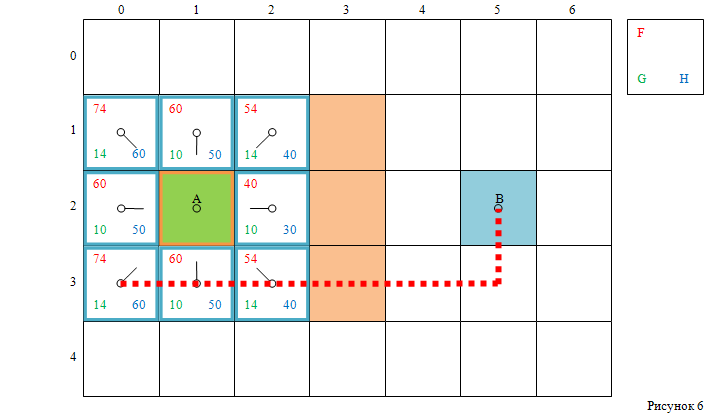
Величина F для каждой клетки вычисляется по формуле (1), как сумма величин G и H.
Для продолжения поиска кратчайшего пути выбирается ячейка из открытого списка с наименьшим значением F.
И для этой клетки выполняются следующие действия (продолжение описанных выше):
- Удаляем выбранную клетку из открытого списка и добавляем её в закрытый список.
- Добавляем в открытый список все соседние к ней клетки, если они ещё не находятся в нём
(игнорируя непроходимые клетки и клетки из закрытого списка).
Указываем, что текущая клетка — родительская, и вычисляем значения G, H и F. - Если соседняя клетка уже находится в открытом списке,
сравниваем значение G у неё и у текущей проверяемой клетки: - если прежнее значение G меньше нового, то ничего не делаем;
- если новое значение G меньше, то обновляем G и меняем родителя на текущую клетку.
Рассмотрим описанные шаги. Сейчас в открытом списке находится 8 клеток,
а стартовая клетка — в закрытом списке.
Следующей для рассмотрения станет клетка с наименьшим значением F —
это клетка с индексами [2, 2] (см. рисунок 7).
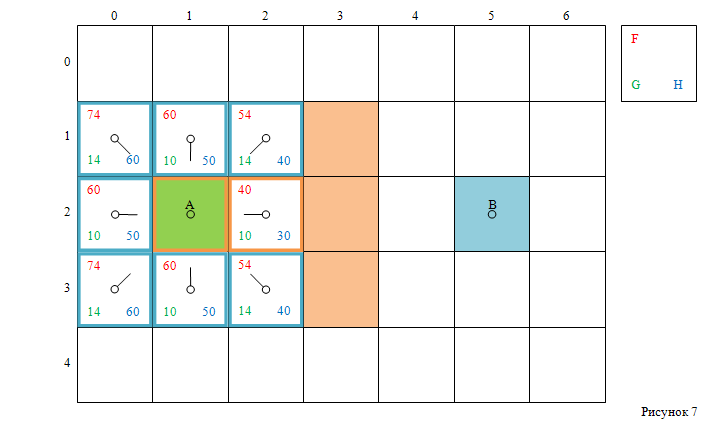
Вначале текущую клетку (с индексами [2, 2]) удаляем из открытого списка
и помещаем в закрытый список (поэтому на рисунке 7 она отмечена оранжевым цветом).
Затем проверяем соседние клетки.
Четыре из них игнорируем – это:
- три непроходимые клетки стены,
- и стартовая клетка, находящаяся в закрытом списке.
Оставшиеся четыре клетки уже находятся в открытом списке,
поэтому необходимо сравнить их значения G со значением G,
которое получилось бы при проходе к ним через текущую клетку.
-
Значение G у клетки ниже текущей (с индексами [3, 2]) равно 14,
а значение G, полученное при проходе через текущую клетку — 20
(G = 10 у текущей клетки, плюс 10 — путь до нижней клетки).
Поскольку 14 < 20, значение G обновлять не нужно. -
У клетки слева внизу (с индексами [3, 1]) G = 10,
а значение G через текущую клетку — 24
(G = 10 у текущей, плюс 14 — путь по диагонали).
Так как 24 > 10, обновление G также не требуется. -
Аналогично проверяются:
- клетка выше текущей (с индексами [1, 2]),
- и клетка слева вверху (с индексами [1, 1]).
После того как все соседние клетки рассмотрены,
можно двигаться дальше.
В данный момент в открытом списке находятся 7 клеток,
две из которых имеют одинаковое наименьшее значение F = 54.
Какую клетку выбрать следующей — не важно для алгоритма,
поэтому считаем, что случайно выбрана клетка справа внизу от стартовой
(с индексами [3, 2]) — как показано на рисунке 8.
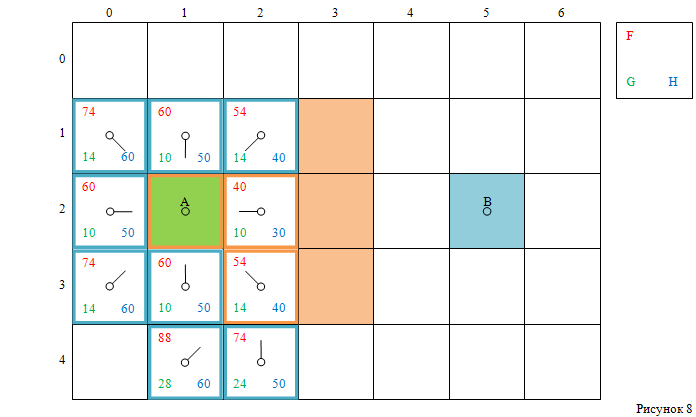
Проверяя клетки, соседние к текущей клетке,
клетки с индексами [2, 3] и [3, 3] — игнорируем,
так как они непроходимы.
Клетку с индексами [2, 2] и стартовую клетку также игнорируем,
так как они находятся в закрытом списке.
Клетку с индексами [4, 3] также игнорируем,
так как к ней нельзя добраться без среза угла ближайшей стены.
– Сначала необходимо перейти на клетку с индексами [4, 2],
а потом уже на [4, 3].
(Примечание: Правило, запрещающее срезать углы препятствий, не является обязательным.
Его применение зависит от расположения вершин.)
Клетка с индексами [3, 1] уже находится в открытом списке,
поэтому сравниваем её значение F со значением F,
если бы пришли к ней через текущую клетку.
Это значения 60 и 64, соответственно.
Так как 60 < 64, обновление не требуется.
Клетки с индексами [4, 1] и [4, 2] — добавляем в открытый список,
предварительно вычислив значения G, H и F,
а также установив указатель на родительскую клетку
(см. рисунок 8).
Повторяем описанную выше методику,
пока не добавим целевую клетку в открытый список.
Следующая клетка в открытом списке с наименьшим значением F = 54 —
это клетка с индексами [1, 2].
- Удаляем её из открытого списка,
- добавляем в закрытый список,
- проверяем её соседей
(при этом добавляем клетки с индексами [0, 1] и [0, 2]).
Итог операций проиллюстрирован на рисунке 9.
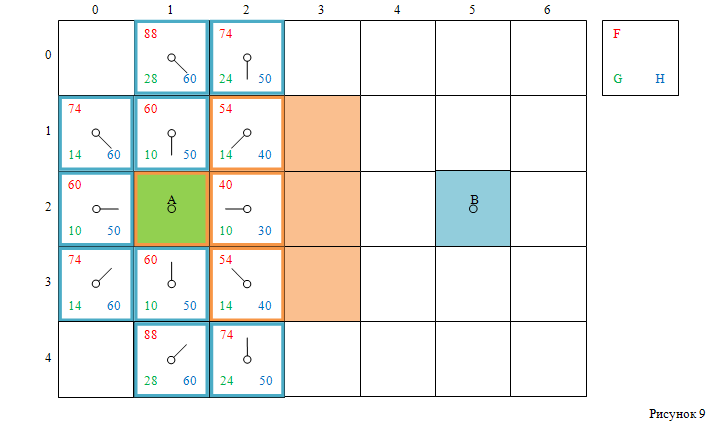
Сейчас в открытом списке находятся две клетки
с наименьшим значением F, равным 60.
Случайным образом выбираем клетку с индексами [3, 1].
- Удаляем её из открытого списка,
- добавляем в закрытый список.
Проверяем её соседей:
-
Добавляем в открытый список клетку с индексами [4, 0].
-
У клетки с индексами [4, 1], которая уже находится в открытом списке,
обновляем значение F и меняем указатель на родителя:
теперь он ссылается на текущую клетку с индексами [3, 1].
Смотри рисунок 10:
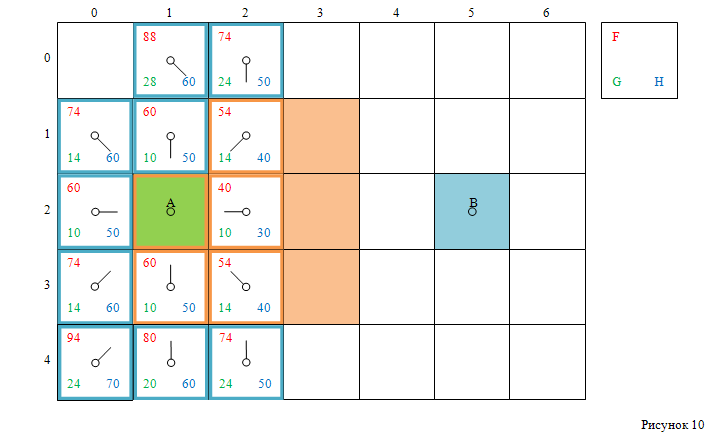
Следующую из **открытого списка** обрабатываем **клетку с индексами [2, 0]**.
- **Удаляем её из открытого списка**,
- **добавляем в закрытый список**.
При этом **никакие из её соседних клеток не нуждаются в обновлении**
(смотри **рисунок 11**):
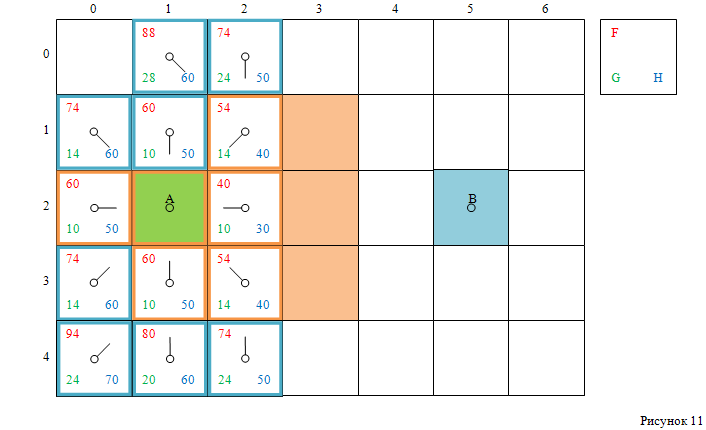
Далее обрабатываем клетку с индексами [1, 1].
- Удаляем её из открытого списка,
- добавляем в закрытый список.
При этом:
- обновляем данные её соседней клетки с индексами [0, 1],
- добавляем в открытый список клетку с индексами [0, 0].
Смотри рисунок 12:
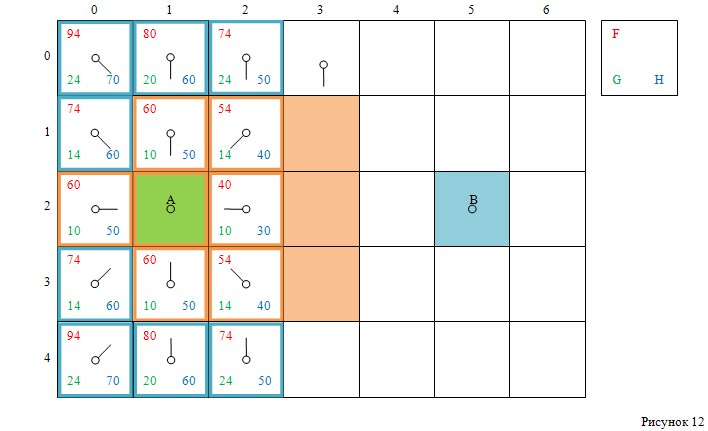
Следующие клетки в открытом списке имеют наименьшее значение F, равное 74.
Случайным образом выбираем клетку с индексами [4, 2].
- Удаляем её из открытого списка,
- добавляем в закрытый список.
Проверяем её соседей:
- добавляем в открытый список клетку с индексами [4, 3].
Смотри рисунок 13:
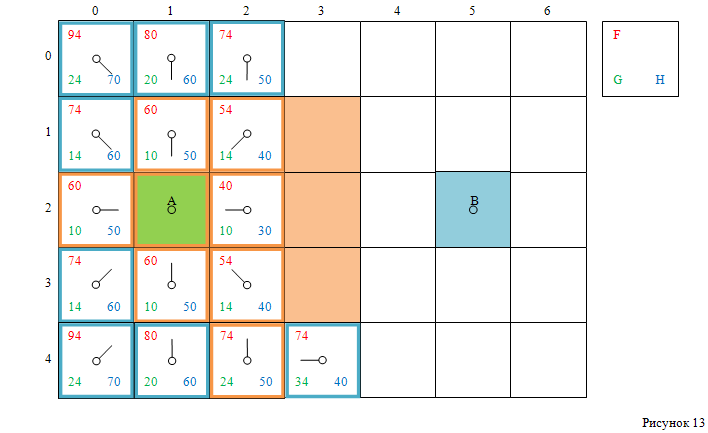
Предположим, что следующей клеткой с наименьшим значением F выбрана клетка, ближе к той, которую проверяли перед этим – клетка с индексами [4, 3].
- Удаляем её из открытого списка,
- добавляем в закрытый список.
Обрабатываем её соседние клетки (рисунок 14):
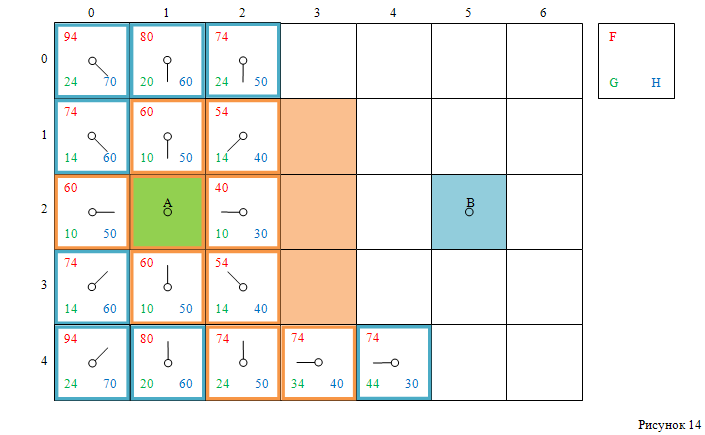
Далее, выбираем клетку с индексами [4, 4], удаляем её из открытого списка, добавляем в закрытый список. Обрабатываем её соседние клетки – добавляем три клетки в открытый список (клетки с индексами [3, 4], [3, 5] и [5, 4]) (рисунок 15).
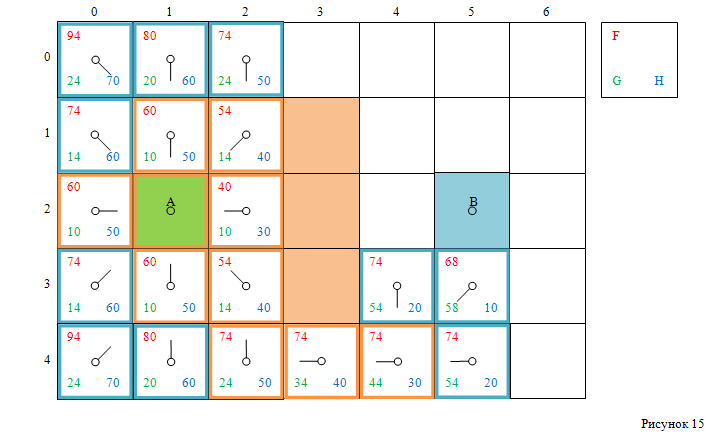
Следующая клетка с наименьшим значением F — это клетка с индексами [3, 5]. Выбираем её, удаляем из открытого списка, добавляем в закрытый список. Обрабатываем её соседние клетки, при этом в открытый список добавляются клетки с индексами [2, 4], [3, 6], [2, 6] и целевая клетка с индексами [2, 5]. Смотри рисунок 16.
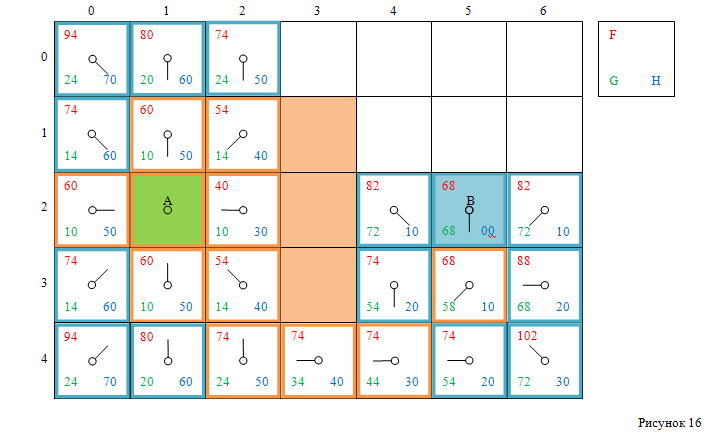
Целевая клетка находится в открытом списке, а это значит, что был найден путь от стартовой до финишной клетки. Теперь, следуя указателям на родителей, можно пройти от финишной клетки до стартовой клетки, а сохранённый путь в обратном направлении – путь от стартовой до целевой клетки. Это и будет найденный кратчайший путь (рисунок 17).
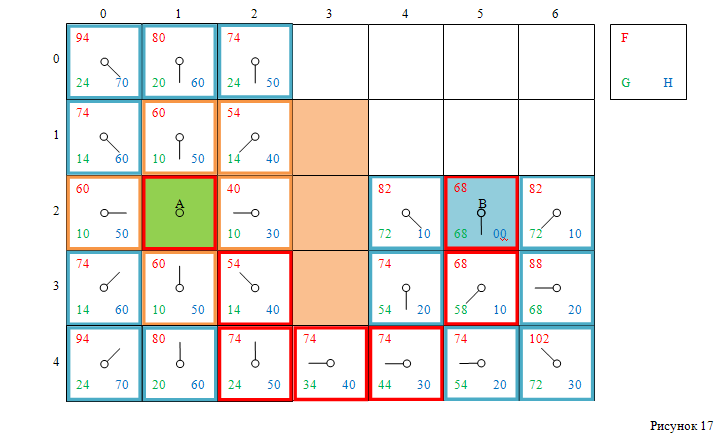
Пошаговое представление метода:#
-
Добавить стартовую клетку в открытый список (при этом её значения G, H и F равны 0).
-
Повторять следующие шаги:
- Ищем в открытом списке клетку с наименьшим значением величины F, делаем её текущей.
- Удаляем текущую клетку из открытого списка и помещаем в закрытый список.
-
Для каждой из соседних клеток, к текущей клетке:
- Если клетка непроходима или находится в закрытом списке, игнорируем её.
- Если клетка не в открытом списке, то добавляем её в открытый список, при этом рассчитываем для неё значения G, H и F, и также устанавливаем ссылку родителя на текущую клетку.
- Если клетка находится в открытом списке, то сравниваем её значение G со значением G, таким, что если бы к ней пришли через текущую клетку. Если сохранённое в проверяемой клетке значение G больше нового, то меняем её значение G на новое, пересчитываем её значение F и изменяем указатель на родителя так, чтобы она указывала на текущую клетку.
-
Останавливаемся, если:
- В открытый список добавили целевую клетку (в этом случае путь найден).
- Открытый список пуст (в этом случае к целевой клетке пути не существует).
-
Сохраняем путь, двигаясь назад от целевой точки, проходя по указателям на родителей до тех пор, пока не дойдём до стартовой клетки.
Сравнение#
Сравните алгоритмы: алгоритм Дейкстры вычисляет расстояние от начальной точки. Жадный поиск по первому наилучшему совпадению оценивает расстояние до точки цели. A* использует сумму этих двух расстояний.
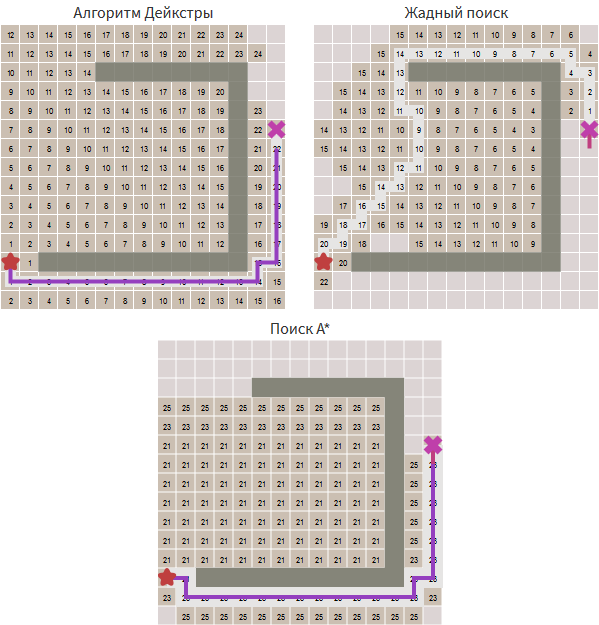
Обрратимся к великолепной визуализации пользователя honzaap, сам проект доступен по ссылке
Реализация в коде#
import heapq
class Node:
def __init__(self, x, y, g=0, h=0, parent=None):
self.x = x
self.y = y
self.g = g # стоимость пути от начальной клетки
self.h = h # эвристическая оценка до целевой клетки
self.f = g + h # общая оценка F
self.parent = parent
def __lt__(self, other):
return self.f < other.f
def manhattan_distance(x1, y1, x2, y2):
return abs(x1 - x2) + abs(y1 - y2)
def a_star(grid, start, goal):
open_list = []
closed_list = set()
start_node = Node(start[0], start[1], 0, manhattan_distance(start[0], start[1], goal[0], goal[1]))
heapq.heappush(open_list, start_node)
while open_list:
current_node = heapq.heappop(open_list)
if (current_node.x, current_node.y) == goal:
path = []
while current_node:
path.append((current_node.x, current_node.y))
current_node = current_node.parent
return path[::-1]
closed_list.add((current_node.x, current_node.y))
for dx, dy in [(-1, 0), (1, 0), (0, -1), (0, 1)]: # движения по вертикали и горизонтали
nx, ny = current_node.x + dx, current_node.y + dy
if 0 <= nx < len(grid) and 0 <= ny < len(grid[0]) and grid[nx][ny] == 0 and (nx, ny) not in closed_list:
g = current_node.g + 1
h = manhattan_distance(nx, ny, goal[0], goal[1])
neighbor = Node(nx, ny, g, h, current_node)
heapq.heappush(open_list, neighbor)
return None # Нет пути
# Пример использования:
grid = [
[0, 0, 0, 0, 0],
[0, 1, 1, 0, 0],
[0, 0, 0, 1, 0],
[0, 1, 0, 0, 0],
[0, 0, 0, 0, 0]
]
start = (0, 0)
goal = (4, 4)
path = a_star(grid, start, goal)
print(path)
#include <iostream>
#include <vector>
#include <queue>
#include <unordered_set>
#include <utility>
#include <algorithm>
#include <string> // Добавлен этот заголовок для std::to_string
using namespace std;
struct Node {
int x, y;
int g; // стоимость пути от начальной клетки
Node* parent;
Node(int x, int y, int g = 0, Node* parent = nullptr)
: x(x), y(y), g(g), parent(parent) {}
};
struct CompareNode {
bool operator()(const Node* a, const Node* b) const {
return a->g > b->g; // для min-heap по g (как в Дейкстре)
}
};
vector<pair<int, int>> dijkstra(const vector<vector<int>>& grid,
const pair<int, int>& start,
const pair<int, int>& goal) {
priority_queue<Node*, vector<Node*>, CompareNode> open_list;
unordered_set<string> closed_list;
Node* start_node = new Node(start.first, start.second, 0);
open_list.push(start_node);
const vector<pair<int, int>> directions = { {-1, 0}, {1, 0}, {0, -1}, {0, 1} };
while (!open_list.empty()) {
Node* current_node = open_list.top();
open_list.pop();
if (current_node->x == goal.first && current_node->y == goal.second) {
vector<pair<int, int>> path;
while (current_node != nullptr) {
path.emplace_back(current_node->x, current_node->y);
current_node = current_node->parent;
}
reverse(path.begin(), path.end());
return path;
}
string key = to_string(current_node->x) + "," + to_string(current_node->y);
if (closed_list.count(key)) {
delete current_node;
continue;
}
closed_list.insert(key);
for (const auto& dir : directions) {
int nx = current_node->x + dir.first;
int ny = current_node->y + dir.second;
if (nx >= 0 && nx < grid.size() && ny >= 0 && ny < grid[0].size() &&
grid[nx][ny] == 0) {
string new_key = to_string(nx) + "," + to_string(ny);
if (!closed_list.count(new_key)) {
int new_g = current_node->g + 1;
Node* neighbor = new Node(nx, ny, new_g, current_node);
open_list.push(neighbor);
}
}
}
}
return {}; // Нет пути
}
int main() {
vector<vector<int>> grid = {
{0, 0, 0, 0, 0},
{0, 1, 1, 0, 0},
{0, 0, 0, 1, 0},
{0, 1, 0, 0, 0},
{0, 0, 0, 0, 0}
};
pair<int, int> start = { 0, 0 };
pair<int, int> goal = { 4, 4 };
auto path = dijkstra(grid, start, goal);
cout << "Path: ";
for (const auto& p : path) {
cout << "(" << p.first << ", " << p.second << ") ";
}
cout << endl;
return 0;
}
Связанные темы#
Задача о рюкзаке
стр 185-226 Грокаем алгоритмы. Иллюстрированное пособие для программистов и любопытствующих. - СПб.: Питер, 2017. - 288 с.: ил. - (Серия «Библиотека программиста»). ISBN 978-5-496-02541-6
Для желающих продолжить
Пасхалку найти довольно легко достаточно вбить адрес:
https://ratcatcher.ru/media/alg/practice/prac_11/{РёРјСЏ РєРѕРјРёРєСЃР°}.html
Р?РјСЏ РєРѕРјРёРєСЃР° РІС‹ уже сможете сами посмотреть
Ваша задача прислать мне наиболее оптимальную стратегию игры с ботом, на ваш взгляд, зная, что он работает с марковским процессом. Удачи!
1251