Практика 10. Задача о кратчайшем пути

Данные для работы

Определение.
Кратчайшим путём между вершинами a и b в неориентированном графе называется путь между ними, содержащий наименьшее количество рёбер.

В зависимости от контекста, под длиной пути могут понимать:

• количество рёбер:
  

  k
  

• количество промежуточных вершин:
  

  k - 1
  

• количество всех вершин на пути, включая начальную и конечную:
  

  k + 1
  

Кратчайший путь между парой вершин может быть не единственным.

---

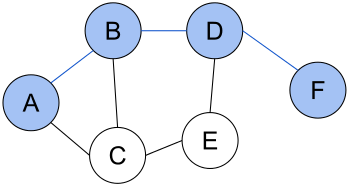
Определение.
Взвешенным графом называется граф, в котором каждому ребру сопоставляется число — вес, длина или стоимость ребра.

Во взвешенных графах длина пути определяется как сумма длин всех рёбер, входящих в путь:

w(p) = \sum_{i=1}^{k} w(v_{i-1}, v_i)

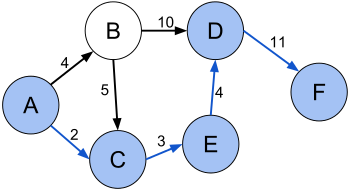
Несмотря на то, что в выделенном пути больше рёбер, его суммарная стоимость меньше.

Если не указано иначе, длина ребра может быть любым числом, в том числе отрицательным.
Однако графы с отрицательными рёбрами могут приводить к парадоксальным ситуациям. Например, при наличии цикла отрицательного веса можно проходить по нему сколь угодно много раз, каждый раз уменьшая суммарный вес пути. В этом случае путь между двумя вершинами может иметь произвольно малый вес.

Поэтому, как правило, рассматриваются графы

Пути в ациклических графах, как задача динамического програмирования

Динамическое программирование — это когда у нас есть задача, которую непонятно как решать, и мы разбиваем её на меньшие задачи, которые тоже непонятно как решать.

В отличие от метода разделяй и властвуй мы надеемся на оптимальность нашего выбора, но не гарантируем её! Почему же так? Давайте порассуждаем о графах.

Если в графе нет циклов, то задача поиска кратчайших путей значительно упрощается.

В этом случае кратчайшие расстояния от заданной вершины до всех остальных можно находить в стиле динамического программирования.
Для любой вершины v значение кратчайшего расстояния можно выразить через перебор всех возможных последних рёбер на кратчайшем пути:

d_v = \min_{(u, v) \in E} (d_u + w(u, v))

Здесь:

• math d_v — кратчайшее расстояние от начальной вершины до вершины v,
• math (u, v) — ребро, завершающее путь к v,
• math w(u, v) — вес этого ребра.

Для корректного применения этой формулы нужно обеспечить два условия:

1. Для каждой вершины v уметь находить все входящие в неё рёбра, то есть просматривать все такие u, для которых math (u, v) \in E.
2. Обрабатывать вершины в таком порядке, чтобы при вычислении math d_v все необходимые math d_u уже были подсчитаны.

Note

Зафиксируем простое, но важное свойство: любая часть кратчайшего пути есть кратчайший путь.

Алгоритм поиска в ширину в контекте кратчайшего пути

На прошлом занятии особое внимание было уделено алгоритму поиска в ширину (BFS — breadth-first search).
Как уже обсуждалось, этот алгоритм позволяет находить пути минимальной длины (по числу рёбер) от заданной вершины до всех достижимых. Иначе говоря, поиск в ширину решает задачу нахождения кратчайших путей в графах, где все рёбра имеют одинаковый вес.

Если же граф описывает, например, дорожную сеть (где вершины — населённые пункты, а рёбра — дороги), то для нахождения пути с минимальной длиной имеет смысл учитывать различия между рёбрами. В таких случаях вводится весовая функция:

w: E \to \mathbb{R}

которая каждой паре смежных вершин (ребру) ставит в соответствие вещественное число — вес.
В задачах маршрутизации обычно используют неотрицательные веса, соответствующие длинам дорог. Однако для абстрактных задач (например, моделирования состояний компании, где переход между состояниями сопровождается убытками или прибылью) разумно допускать отрицательные веса.

Весом пути
p = (v₀, v₁, ..., v_k)
называется сумма весов всех рёбер, по которым проходит путь:

w(p) = \sum_{i=1}^{k} w(v_{i-1}, v_i)

Вес кратчайшего пути из вершины u в вершину v определяется выражением:

\delta(u, v) =
\begin{cases}
\min \{ w(p) \mid p: u \leadsto v \}, & \text{если путь из } u \text{ в } v \text{ существует}, \\
\infty, & \text{иначе}
\end{cases}

Допущение отрицательных весов рёбер требует осторожности. Если в графе присутствуют циклы отрицательного веса, то задача теряет смысл: проходя по такому циклу многократно, можно уменьшать вес пути сколь угодно сильно. В таких случаях вес кратчайшего пути считается неопределённым (равным минус бесконечности).

При реализации алгоритмов поиска кратчайших путей сохраняется информация о предшественниках вершин, как это делалось в BFS и DFS. Это позволяет восстановить путь и построить так называемый подграф предшествования.

Если требуется найти кратчайшие пути из вершины s во все остальные, то подграф предшествования G_π = (V_π, E_π) задаётся так:

• Множество вершин:

V_{\pi} = \{ v \in V \mid \pi[v] \ne \text{NIL} \} \cup \{ s \}

• Множество рёбер:

E_{\pi} = \{ (\pi[v], v) \in E \mid v \in V_{\pi} \setminus \{ s \} \}

Этот подграф содержит все вершины, для которых найден предшественник, а также стартовую вершину s. Он представляет собой дерево (или лес, если граф несвязный), отображающее структуру кратчайших путей от s.

Алгоритм Дейкстры

Алгоритм Дейкстры можно представить как итеративный алгоритм.
Начиная с неизвестных расстояний до всех остальных вершин, итерации этого алгоритма постепенно уточняют и улучшают эти расстояния, так что к моменту завершения алгоритма он приходит к искомому ответу.

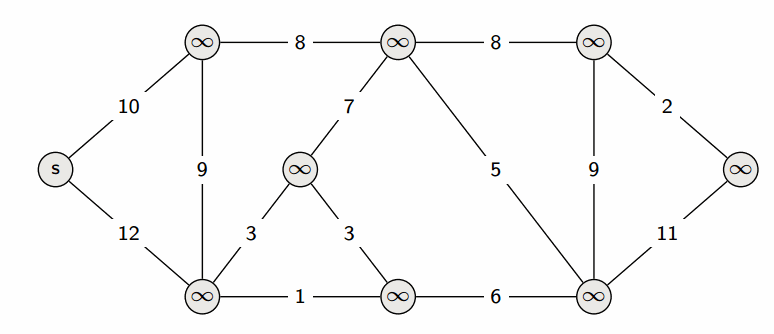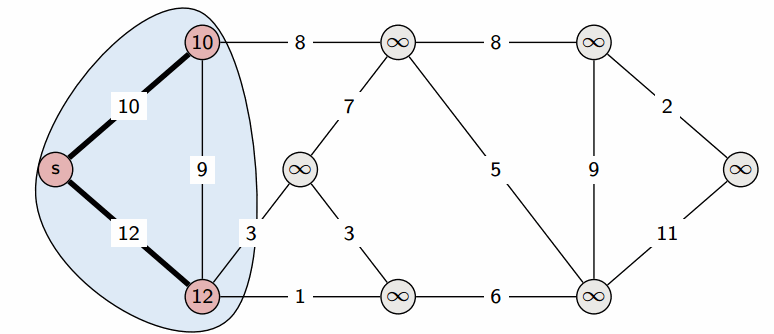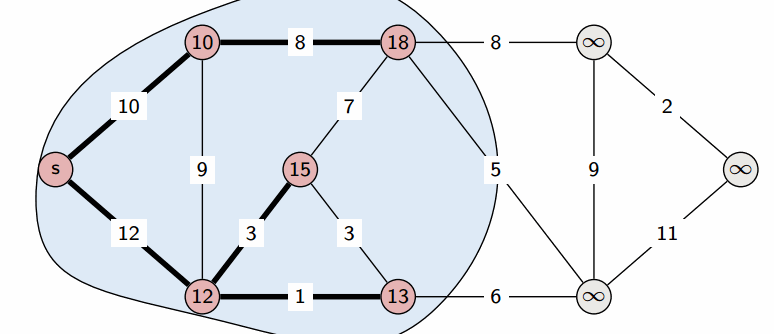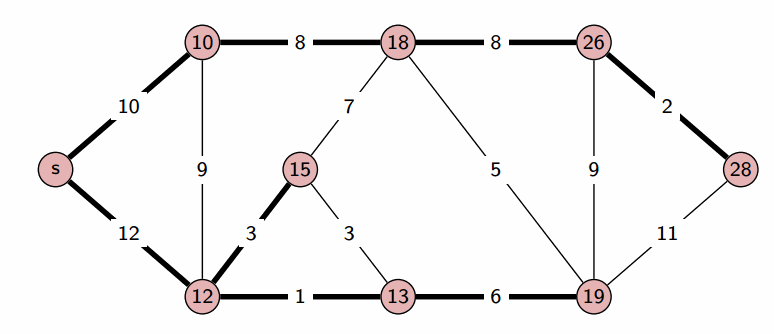
Пошаговое описание алгоритма:

1. Заведём массив текущих расстояний dist и массив отметок посещённых вершин visited.
   Изначально массив dist заполнен значениями "бесконечность", кроме стартового элемента dist[s], равного нулю.
   Массив отметок visited заполнен значениями false.

2. Изо всех не посещённых пока вершин выбирается вершина v с наименьшим значением dist:
   $$v := \mathop{\arg\min}_{1 \le i \le n,\; \text{visited}[i] = \text{false}} \text{dist}[i]$$

3. Выбранная вершина v отмечается посещённой:
   visited[v] := true

4. Просматриваются все рёбра, исходящие из вершины v, и вдоль каждого ребра производится релаксация — попытка улучшить текущее расстояние до новой вершины.
   Если конец текущего ребра обозначить как t, а его вес — как c, то выполняется:
   $$\text{dist}[t] := \min(\text{dist}[t],\; \text{dist}[v] + c)$$

5. Если больше не осталось непосещённых вершин с конечным расстоянием, алгоритм завершает работу.
   Иначе — переход к шагу 2.

Warning

Алгоритм Дейкстры применим только в том случае, когда веса всех ребер неотрицательны.

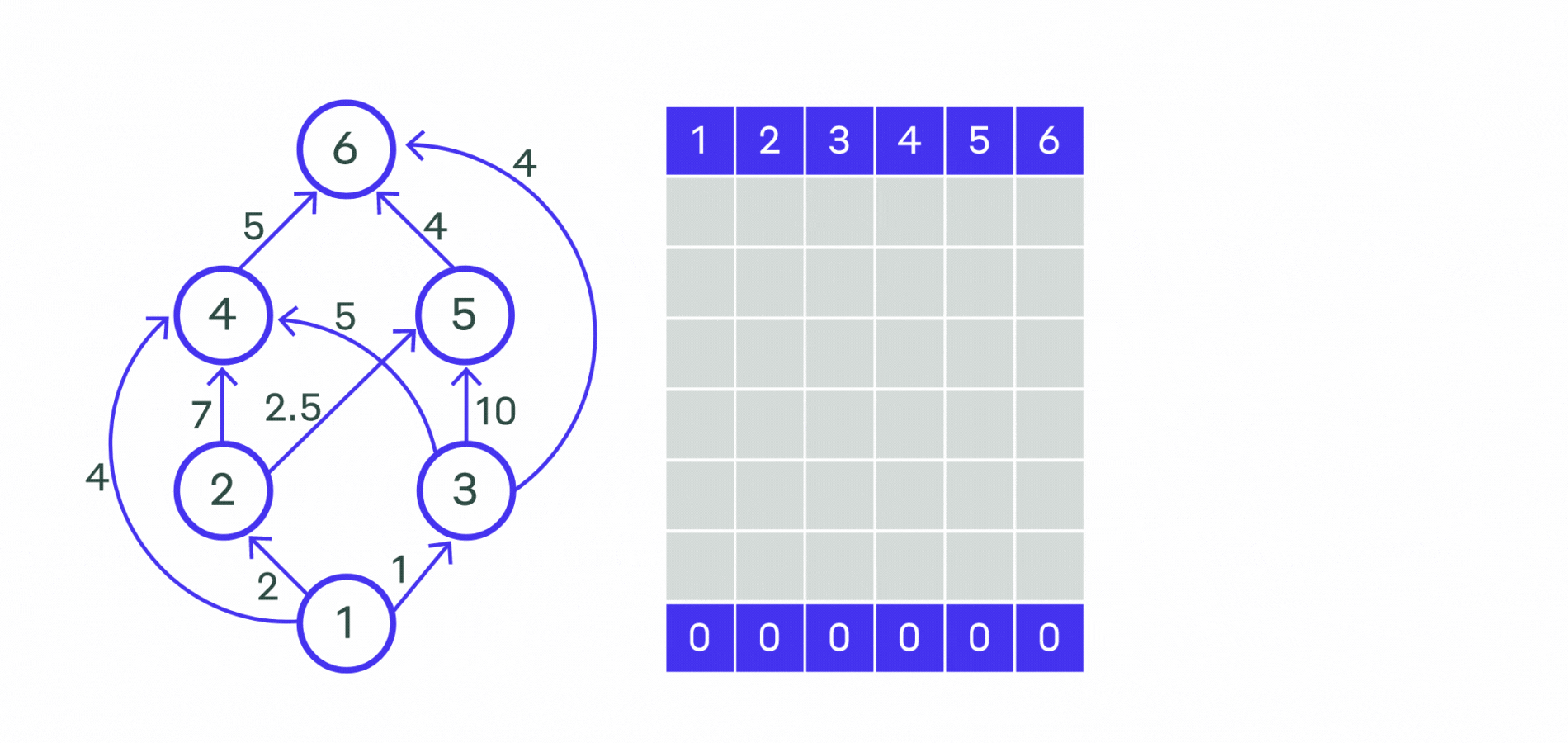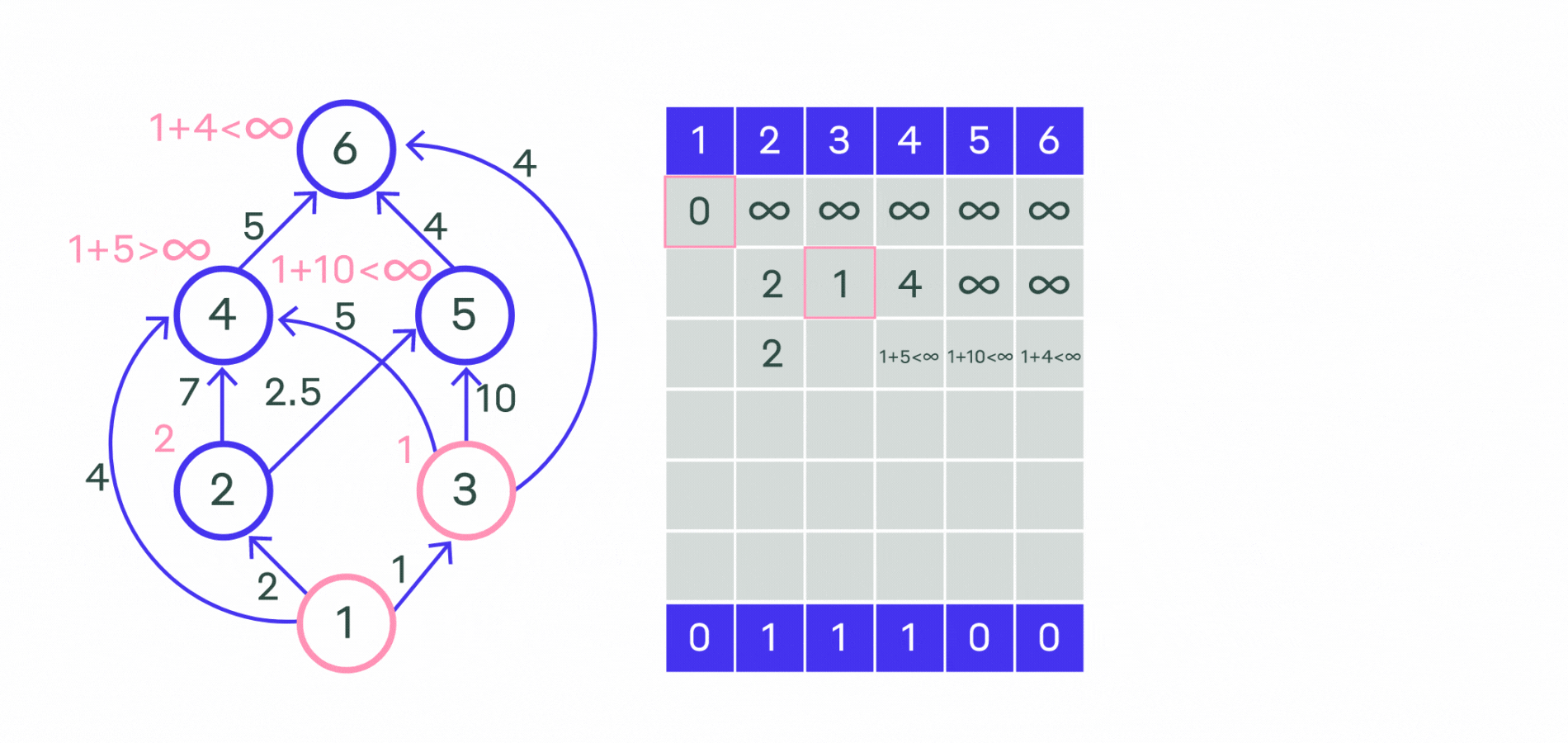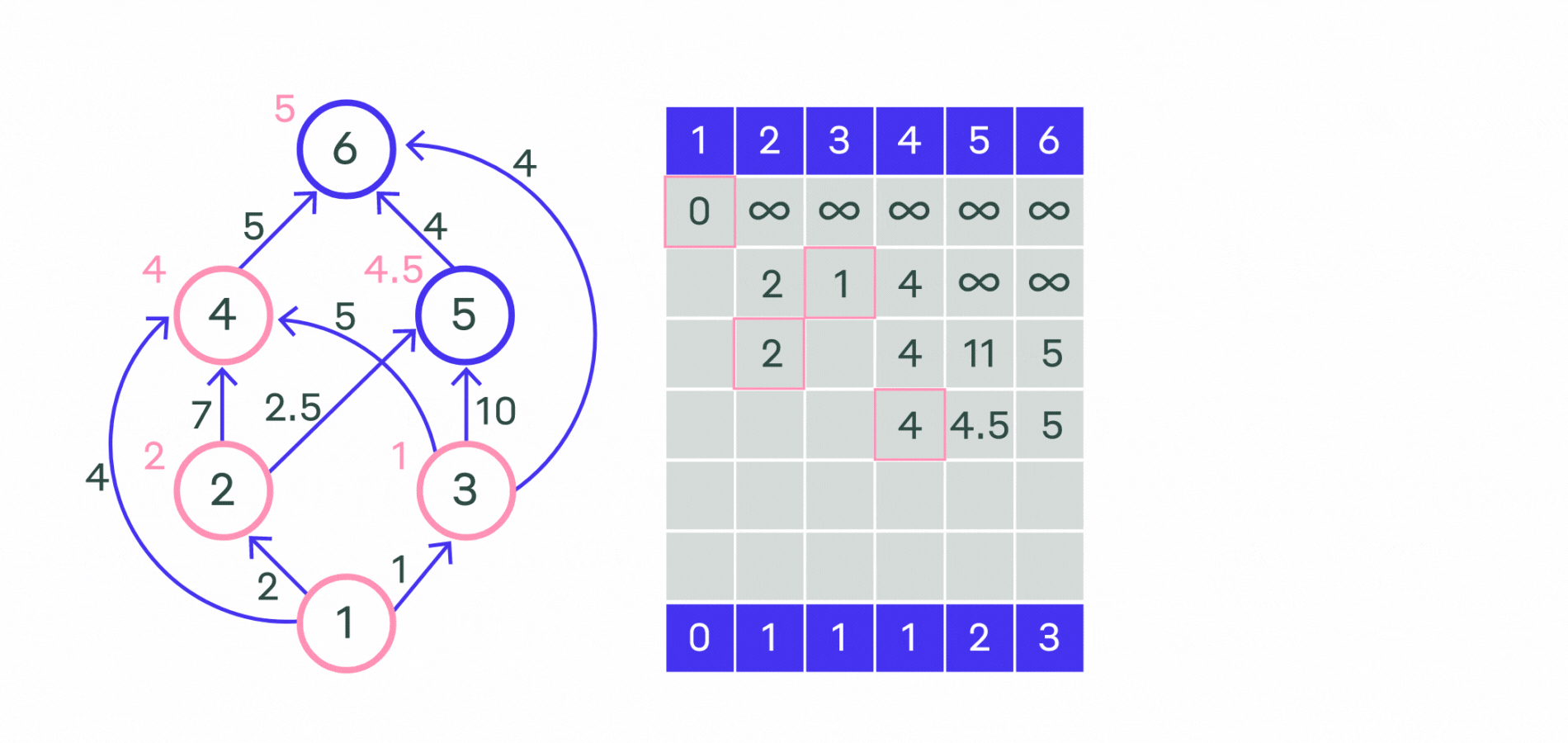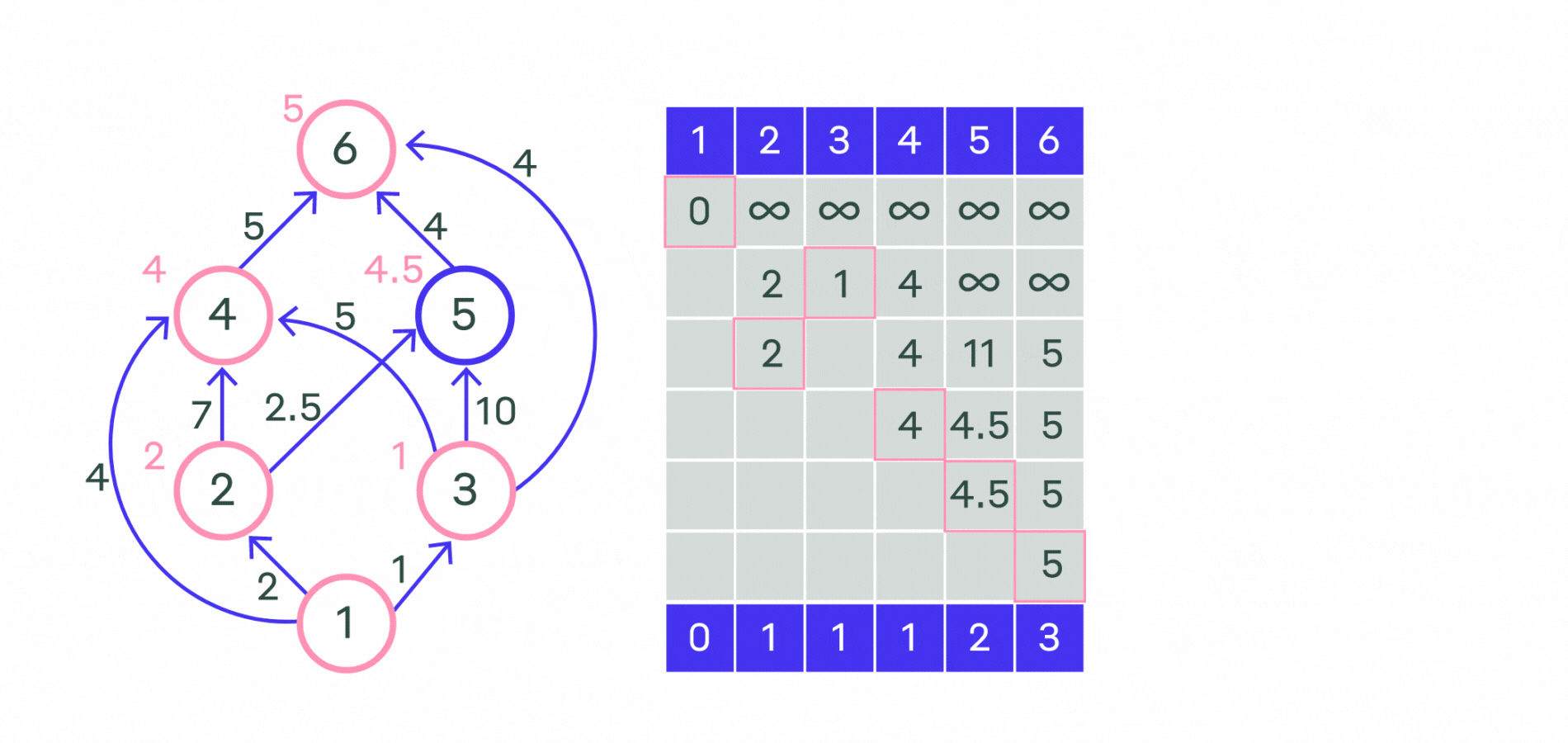
Более алгоритмическое объяснение

Заведём массив d, в котором для каждой вершины v будем хранить текущую длину $d_v$ кратчайшего пути из вершины $s$ в вершину $v$.
Изначально $d_s = 0$, а для всех остальных вершин расстояние равно бесконечности (или любому числу, которое заведомо больше максимально возможного расстояния).

Во время работы алгоритма мы будем постепенно обновлять этот массив, находя более оптимальные пути к вершинам и уменьшая расстояние до них.
Когда мы узнаем, что найденный путь до какой-то вершины $v$ оптимальный, мы будем помечать эту вершину, поставив единицу $a_v = 1$ в специальном массиве $a$, изначально заполненном нулями.

Сам алгоритм состоит из $n$ итераций, на каждой из которых выбирается вершина $v$ с наименьшей величиной $d_v$ среди ещё не помеченных:

$$v = \mathop{\arg\min}_{u \;|\; a_u = 0} d_u$$

(Заметим, что на первой итерации выбрана будет стартовая вершина $s$.)

Выбранная вершина отмечается в массиве $a$, после чего из вершины $v$ производятся релаксации: просматриваем все исходящие рёбра $(v, u)$ и для каждой такой вершины $u$ пытаемся улучшить значение $d_u$, выполнив присвоение:

$$d_u = \min(d_u, d_v + w)$$

где $w$ — длина ребра $(v, u)$.

На этом текущая итерация заканчивается, и алгоритм переходит к следующей: снова выбирается вершина с наименьшей величиной $d$, из неё производятся релаксации, и так далее.
После $n$ итераций все вершины графа станут помеченными, и алгоритм завершает свою работу.

Поробуйте сами

В чем возможна вариабильность времени работы?

Единственное вариативное место в алгоритме, от которого зависит его сложность — как конкретно искать v с минимальным dv.

Восстановление путей

Алгоритм Дейкстры в базовой версии вычисляет только минимальные расстояния от стартовой вершины до всех остальных, но сам путь до этих вершин не сохраняется. Чтобы иметь возможность восстановить кратчайший путь, алгоритм можно немного доработать.

Для этого вводится дополнительный массив parent, в котором для каждой вершины i будет храниться номер вершины, из которой в ходе работы алгоритма был получен наилучший (т.е. кратчайший) путь в i. Другими словами, parent[i] — это предыдущая вершина на кратчайшем пути от стартовой до i.

Массив parent обновляется в процессе релаксации рёбер: если расстояние до вершины t удаётся улучшить через вершину v, то выполняется не только обновление расстояния, но и присваивание parent[t] = v.

После завершения алгоритма мы можем восстановить кратчайший путь от стартовой вершины s до любой вершины i, просто двигаясь в обратном порядке — от i к parent[i], затем к parent[parent[i]] и так далее, пока не дойдём до s. Для удобства начальной вершине задают parent[s] = -1, чтобы понимать, где остановиться.

---

Пример: пусть нужно восстановить путь от вершины 1 до вершины 4. Пусть массив parent содержит такие значения:
- parent[4] = 2
- parent[2] = 3
- parent[3] = 1
- parent[1] = -1

Тогда восстановление пути будет происходить так:

1. Начинаем с вершины 4, добавляем её в путь.
2. Переходим к parent[4] = 2, добавляем вершину 2.
3. Переходим к parent[2] = 3, добавляем вершину 3.
4. Переходим к parent[3] = 1, добавляем вершину 1.
5. parent[1] = -1, восстановление завершено.

Итог: кратчайший путь от вершины 1 до 4 — это последовательность:
1 → 3 → 2 → 4

Реализация для плотных графов

Воспользуемся чтением графа с прошлого занятия и немного модифицируем.

Вначале идет чтение входных данных и построение графа в виде списков смежности. Поскольку граф взвешенный, каждый элемент списка смежности — это
пара чисел: номер вершины, в которую ведет ребро, и вес ребра.

PythonC++

def read_graph():
    vertex_count, edge_count = map(int, input().split())
    adj_list = [[] for _ in range(vertex_count)]
    for _ in range(edge_count):
        vertex_from, vertex_to, price = map(int, input().split())
        vertex_from -= 1
        vertex_to -= 1
        adj_list[vertex_from].append((vertex_to, price))
return adj_list, vertex_count

#include <iostream>
#include <vector>
#include <utility>
#include <algorithm>
using namespace std;

using Edge = pair<int, int>;
using Graph = vector<vector<Edge>>;

Graph read_graph(int& vertex_count, int& edge_count) {
    cin >> vertex_count >> edge_count;
    Graph adj_list(vertex_count);
    for (int i = 0; i < edge_count; ++i) {
        int from, to, weight;
        cin >> from >> to >> weight;
        --from; --to;  // 0-based indexing
        adj_list[from].emplace_back(to, weight);
    }
    return adj_list;
}

Далее происходит инициализация переменных для алгоритма Дейкстры.

PythonC++

dist = [None] * vertex_count
visited = [False] * vertex_count
parent = [None] * vertex_count
dist[start] = 0

int n = adj_list.size();
vector<int> dist(n, -1);
vector<char> visited(n, false);
vector<int> parent(n, -1);
dist[start] = 0;

Задание реализуйте алгоритм Дейсктры

PythonC++

def dijkstra(adj_list, vertex_count, start):
dist = [None] * vertex_count
visited = [False] * vertex_count
parent = [None] * vertex_count
dist[start] = 0

# ВАШ КОД

return dist, parent

pair<vector<int>, vector<int>> dijkstra(const Graph& adj_list, int start) {
int n = adj_list.size();
vector<int> dist(n, -1);
vector<char> visited(n, false);
vector<int> parent(n, -1);
dist[start] = 0;

// ваш код

return {dist, parent};
}

Функция для восстановления путей

PythonC++

def restore_path(parent, finish):
    path = []
    v = finish
    while v is not None:
        path.append(v + 1)  # +1 для вывода в 1-индексации
        v = parent[v]
    return list(reversed(path))

vector<int> restore_path(const vector<int>& parent, int finish) {
    vector<int> path;
    for (int v = finish; v != -1; v = parent[v])
        path.push_back(v);
    reverse(path.begin(), path.end());
    return path;
}

Асимптотика такого алгоритма составит $O(n^2)$: на каждой итерации мы находим аргминимум за $O(n)$ и проводим $O(n)$ релаксаций.

Заметим также, что мы можем делать не $n$ итераций, а чуть меньше. Во-первых, последнюю итерацию можно никогда не делать (оттуда ничего уже не прорелаксируешь). Во-вторых, можно сразу завершаться, когда мы доходим до недостижимых вершин ($d_v = \infty$).

Реализация для разреженных графов

Для разрежённых графов, где количество рёбер $t$ значительно меньше, чем $n^2$, использование предыдущей реализации алгоритма Дейкстры будет неэффективным. Основной проблемой является операция выбора вершины $v$ на каждой итерации.

Чтобы ускорить этот процесс, нужна структура данных, которая эффективно поддерживает операции извлечения минимального элемента, добавления и удаления элементов. В стандартной библиотеке C++ для этого подходят структуры данных std::set (основанная на красно-чёрных деревьях) и std::priority_queue (использующая двоичную кучу).

В Python для аналогичных задач используется модуль heapq, который реализует двоичную кучу.

Эти структуры данных позволяют выполнять нужные операции за время $O(\log t)$, что приводит к асимптотике алгоритма Дейкстры $O(t \log t)$. Однако основным ограничением остаётся выполнение релаксаций: в худшем случае будет выполнено $t$ релаксаций, каждая из которых потребует обновления структуры данных за $O(\log n)$.

Что такое двоичная куча?

Двоичная куча (пирамида, сортирующее дерево) — структура данных, представляющая собой двоичное дерево, для которого выполнены три условия:

1. Значение в любой вершине не больше, чем значения её потомков.
2. У любой вершины не более двух сыновей.
3. Слои заполняются последовательно сверху вниз и слева направо, без «дырок».

Реализация для разреженных графов (с использованием двоичной кучи)

Для более эффективной реализации алгоритма Дейкстры с использованием двоичной кучи, мы будем хранить в куче пары вида:

(dist[i], i)

где $i$ — это номер вершины, для которой ещё не определено минимальное расстояние, то есть $visited[i] = \text{false}$.

Двоичная куча — это структура данных, которая поддерживает операции добавления элементов и извлечения минимального элемента. Однако стандартная реализация кучи не предоставляет возможности напрямую изменить значение какого-либо элемента. Это означает, что при релаксации, когда значение $dist[i]$ для вершины $i$ уменьшается, мы не можем просто удалить старую пару из кучи.

Тем не менее, эта проблема не критична, поскольку лишние элементы в куче не повлияют на асимптотику алгоритма. При извлечении минимального элемента мы просто будем игнорировать устаревшие пары, и это не ухудшит производительность.

1. Изначально в куче содержится только одна пара:
   

   (0, s)
   

   
   где $s$ — это стартовая вершина.

2. Для выбора вершины $v$ на каждой итерации алгоритма необходимо извлекать минимальные элементы из кучи до тех пор, пока не найдём пару с актуальным значением расстояния для вершины $v$.

3. При успешной релаксации, когда значение $dist[i]$ для вершины $i$ уменьшается, добавляем в кучу новую пару:
   

   (dist[i], i)
   

В этой реализации нет необходимости в массиве visited, так как сам процесс работы с кучей и извлечение актуальных элементов уже выполняет необходимую роль.

PythonC++

def dijkstra_opt(vertex_count, adj_list, start):
    dist = [None] * vertex_count
    parent = [None] * vertex_count
    dist[start] = 0
    order = []
    heapq.heappush(order, (0, start))

    while order:
        saved_dist, v = heapq.heappop(order)
        if saved_dist != dist[v]:
            continue
        for to, price in adj_list[v]:
            new_d = dist[v] + price
            if dist[to] is None or new_d < dist[to]:
                dist[to] = new_d
                parent[to] = v
                heapq.heappush(order, (dist[to], to))

    return dist, parent

void dijkstra_opt(int vertex_count, const vector<vector<Edge>>& adj_list, int start) {
    // Очередь с приоритетом (min-heap) для хранения пар (расстояние, вершина)
    priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> order;

    // Вектор для хранения минимальных расстояний, инициализация -1 (неопределено)
    vector<int> dist(vertex_count, -1);
    dist[start] = 0; // Начальная вершина имеет расстояние 0
    order.push({0, start}); // Добавляем начальную вершину в очередь

    // Вектор для хранения родителей (предков) каждой вершины
    vector<int> parent(vertex_count, -1);

    while (!order.empty()) {
        int saved_dist = order.top().first;  // Текущее минимальное расстояние
        int v = order.top().second;          // Текущая вершина
        order.pop();

        // Если извлеченный элемент устарел, пропускаем его
        if (dist[v] != saved_dist)
            continue;

        // Проходим по всем соседям вершины v
        for (const Edge& e : adj_list[v]) {
            int to = e.first;     // Соседняя вершина
            int price = e.second; // Стоимость ребра
            int new_d = dist[v] + price;

            // Если найдено лучшее расстояние, обновляем и добавляем в очередь
            if (dist[to] == -1 || new_d < dist[to]) {
                dist[to] = new_d;
                parent[to] = v;
                order.push({new_d, to});
            }
        }
    }

    // Выводим результаты
    for (int i = 0; i < vertex_count; ++i) {
        cout << "Расстояние до вершины " << i << ": " << dist[i] << endl;
    }
    cout << "Массив предков: ";
    for (int i = 0; i < vertex_count; ++i) {
        cout << parent[i] << " ";
    }
    cout << endl;
}

Задание сделать замеры для графа с количеством вершин [100, 200, 300, 400, 500, 600, 700, 800, 900, 1000] и плотностью 0.4

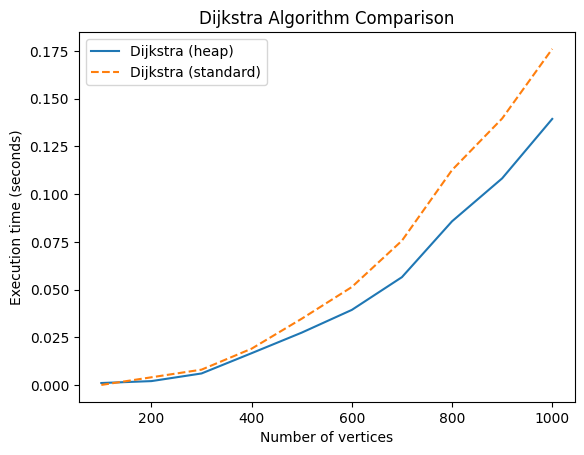
Почему лучше использовать кучу (heap)?

Куча — это структура данных, которая поддерживает приоритеты и идеально подходит для задач, где необходимо часто извлекать минимальные (или максимальные) элементы. В нашем случае, мы всегда ищем вершину с минимальным расстоянием, что делает кучу хорошим выбором.

При применении релаксации (обновлении расстояний до соседних вершин), стандартная версия алгоритма требует перебора всех вершин, чтобы обновить минимальное расстояние, что также может занимать O(V) времени.

С использованием кучи эта операция ограничена O(log V) для каждой вершины, благодаря чему алгоритм становится гораздо быстрее.

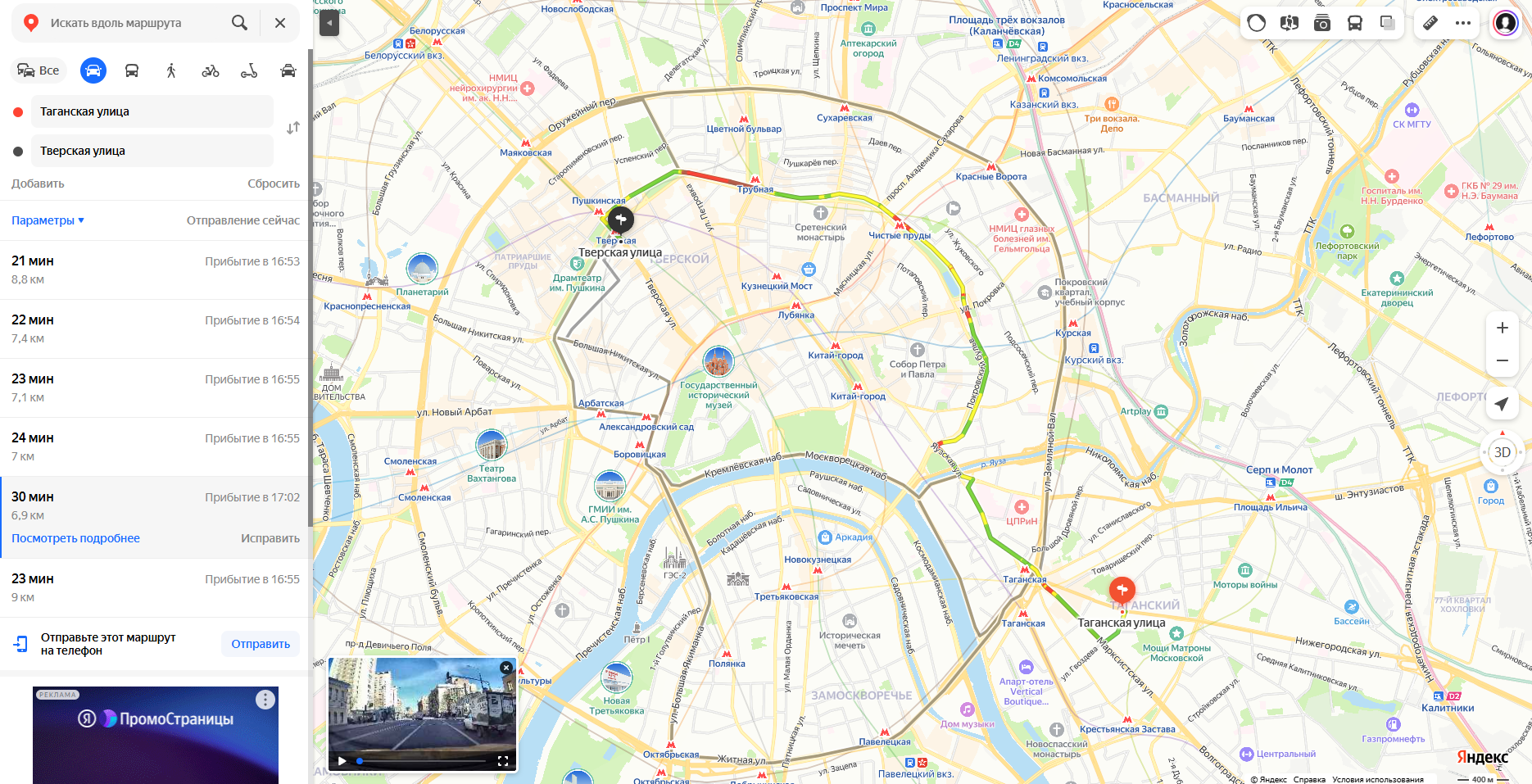
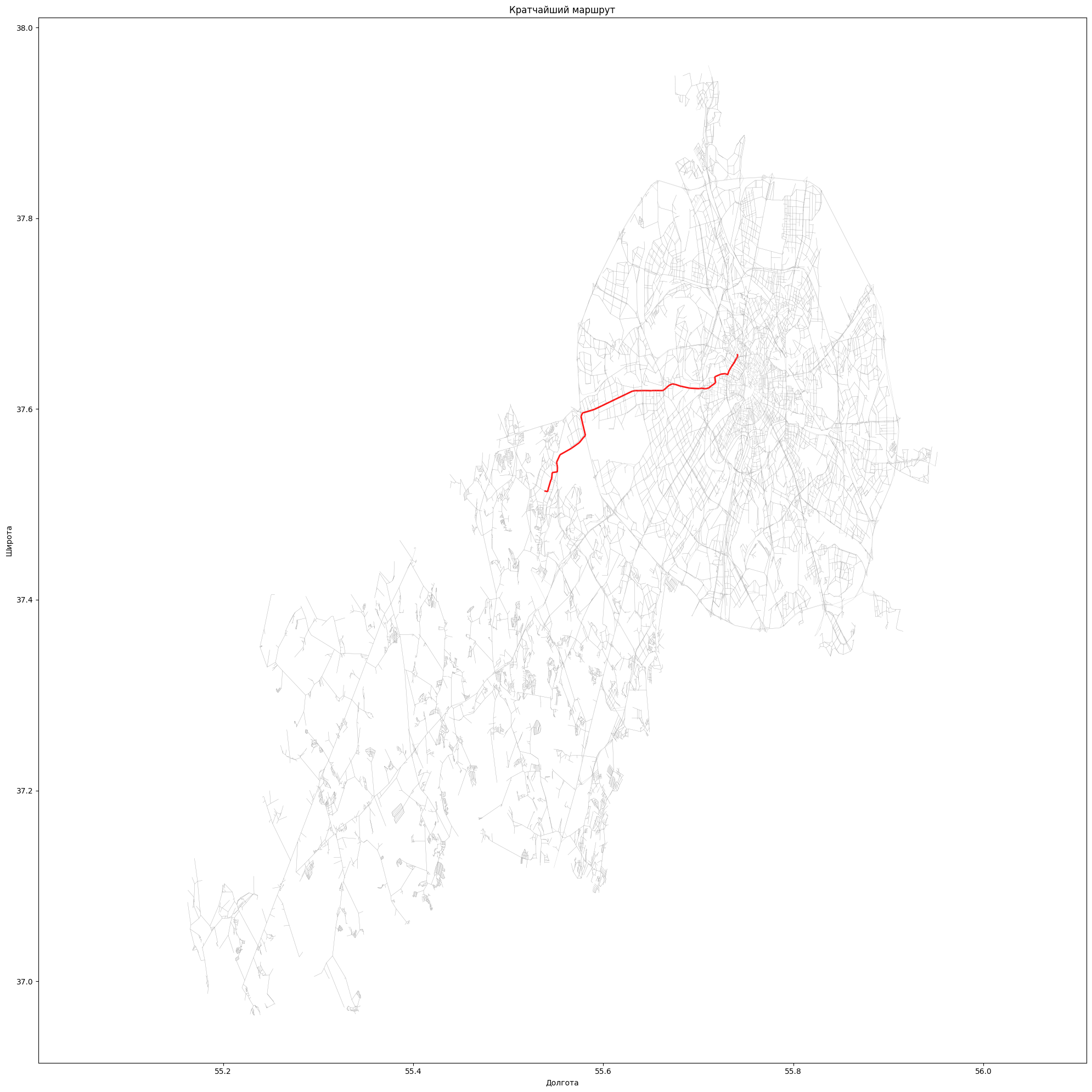
Приложение к реальным данным (Пример Москва)

Представим, что нужно посчитать маршрут от одной точки города до другой. Один из вариантов — это вручную отрисовать все дороги Москвы на Яндекс.Картах, но, как вы понимаете, это решение не очень удобное и трудозатратное.

Но существует гораздо более эффективное решение, использующее данные OpenStreetMap (OSM) — открытого картографического проекта, который предоставляет подробные карты мира, создаваемые и поддерживаемые сообществом пользователей. Этот проект обеспечивает доступ к картографической информации совершенно бесплатно, и можно использовать её для решения задач, таких как нахождение кратчайшего маршрута.

С помощью OpenStreetMap мы можем извлечь все необходимые данные, включая информацию о дорогах, улицах и перекрёстках, и на основе этих данных найти кратчайший маршрут, используя соответствующие алгоритмы.

Таким образом, вместо того чтобы вручную рисовать карту, можно воспользоваться уже готовыми и точными данными, что значительно ускоряет процесс разработки и повышения точности вычислений.

Подробнее о проекте OpenStreetMap:

OpenStreetMap (дословно "открытая карта улиц") — это некоммерческий веб-картографический проект, цель которого — создание подробной, свободной и бесплатной географической карты мира. Карты составляются силами сообщества пользователей интернета, что делает их актуальными и точными.

Пример данных OpenStreetMap:

Запрос данных

Для выполнения дальнейших задач, таких как нахождение кратчайшего маршрута, воспользуемся уже скачанными данными, сформированными при помощи библиотеки Python.
Пример кода для загрузки данных и их сохранения в файл:

import osmnx as ox

# Скачиваем граф по названию города
G = ox.graph_from_place('Москва, Россия', network_type='drive')

# Сохраняем в файл для последующего использования
ox.save_graphml(G, 'moscow_road_network.graphml')

Что такое osmx

OSMnx — пакет для языка Python, который позволяет скачивать, моделировать, анализировать и визуализировать уличные сети и другие геопространственные объекты из OpenStreetMap.

В этом коде мы скачиваем граф уличной сети города Москвы, где учтены только автомобильные дороги (network_type='drive'). После чего сохраняем полученный граф в формате GraphML для последующего использования в анализах и вычислениях. Сохранение данных позволяет избежать повторных загрузок и ускоряет процесс работы с картографической информацией.

Откройте файл moscow_road_network.graphml

О формате graphml

Формат GraphML представляет собой стандарт для обмена графами, который используется для хранения и передачи информации о сетевых структурах, таких как дороги, узлы и связи между ними. Он широко используется благодаря своей гибкости и возможности интеграции с различными программами для анализа графов. GraphML представляет данные в виде XML, что позволяет легко их читать и обрабатывать с использованием различных инструментов.

GraphML включает несколько основных элементов:
- — корневой элемент, который содержит описание графа.
- — элементы, представляющие узлы графа (например, перекрёстки или остановки).
- — элементы, представляющие рёбра графа (например, дороги или маршруты между точками).
- Атрибуты — дополнительные данные, такие как длина дороги, скорость движения, тип дороги и т.д., которые могут быть добавлены как атрибуты для рёбер и узлов.

GraphML является удобным форматом для обмена данными о графах между различными системами и программами, такими как QGIS, Gephi, NetworkX и другие.

Парсим данные

Для парсинга данных воспользуемся библиотеками.
Изучите структуру файла и подставьте что нужно.

PythonC++

import xml.etree.ElementTree as ET

def read_graphml(file_path: str) -> Tuple[Dict[str, Tuple[float, float]], List[Tuple[Tuple[float, float], Tuple[float, float], str]]]:
"""
Читает GraphML файл и возвращает узлы и ребра с названиями улиц

Args:
    file_path: путь к файлу .graphml

Returns:
    Кортеж (nodes, edges), где:
    - nodes: словарь {node_id: (x, y)}
    - edges: список [((x1, y1), (x2, y2), название_улицы), ...]
"""
tree = ET.parse(file_path)
root = tree.getroot()
ns = {'g': 'http://graphml.graphdrawing.org/xmlns'}

nodes = {}
for node in root.findall('.//g:node', ns):
    node_id = node.get('Подставьте что нужно')
    x, y = None, None
    for data in node.findall('.//g:data', ns):
        if data.get('key') == 'Подставьте что нужно':  # x координата (обычно longitude)
            x = float(data.text)
        elif data.get('key') == 'Подставьте что нужно':  # y координата (обычно latitude)
            y = float(data.text)
    if x is not None and y is not None:
        nodes[node_id] = (x, y)

edges = []
for edge in root.findall('.//g:edge', ns):
    source = edge.get('Подставьте что нужно')
    target = edge.get('Подставьте что нужно')
    street_name = None

    for data in edge.findall('.//g:data', ns):
        if data.get('key') == 'Подставьте что нужно':  # название улицы
            street_name = data.text if data.text else None

    if source in nodes and target in nodes:
        edges.append((nodes[source], nodes[target], street_name))

return nodes, edges

    #include "tinyxml2.h"

    std::string utf8_to_cp1251(const std::string& utf8_str) {
        int wide_len = MultiByteToWideChar(CP_UTF8, 0, utf8_str.c_str(), -1, nullptr, 0);
        std::wstring wide_str(wide_len, L'\0');
        MultiByteToWideChar(CP_UTF8, 0, utf8_str.c_str(), -1, &wide_str[0], wide_len);

        int cp1251_len = WideCharToMultiByte(1251, 0, wide_str.c_str(), -1, nullptr, 0, nullptr, nullptr);
        std::string cp1251_str(cp1251_len, '\0');
        WideCharToMultiByte(1251, 0, wide_str.c_str(), -1, &cp1251_str[0], cp1251_len, nullptr, nullptr);

        return cp1251_str;
    }

    tuple<map<string, Coord>, vector<EdgeItem>> read_graphml(const string& file_path) {
    map<string, Coord> nodes;
    vector<EdgeItem> edges;
    SetConsoleCP(1251);
    SetConsoleOutputCP(1251);
    tinyxml2::XMLDocument doc;
    if (doc.LoadFile(file_path.c_str()) != tinyxml2::XML_SUCCESS) {
        std::cerr << "Error loading XML file: " << file_path << endl;
        return make_tuple(nodes, edges);
    }

    tinyxml2::XMLElement* graphml = doc.FirstChildElement("graphml");
    if (!graphml) {
        std::cerr << "Нет файла" << endl;
        return make_tuple(nodes, edges);
    }

    tinyxml2::XMLElement* graph = graphml->FirstChildElement("graph");
    if (!graph) {
        std::cerr << "Нет элементов графа" << endl;
        return make_tuple(nodes, edges);
    }


    for (tinyxml2::XMLElement* node = graph->FirstChildElement("Что тут?"); node; node = node->NextSiblingElement("Что тут?")) {
        const char* id = node->Attribute("Что тут?");
        if (!id) continue;

        double x = 0, y = 0;
        bool has_coords = false;

        for (tinyxml2::XMLElement* data = node->FirstChildElement("Что тут?"); data; data = data->NextSiblingElement("Что тут?")) {
            const char* key = data->Attribute("Что тут?");
            if (!key) continue;

            if (strcmp(key, "Что тут?") == 0) { 
                x = atof(data->GetText());
                has_coords = true;
            }
            else if (strcmp(key, "Что тут?") == 0) { 
                y = atof(data->GetText());
                has_coords = true;
            }
        }

        if (has_coords) {
            nodes[id] = make_pair(x, y);
        }
    }


    for (tinyxml2::XMLElement* edge = graph->FirstChildElement("Что тут?"); edge; edge = edge->NextSiblingElement("Что тут?")) {
        const char* source_id = edge->Attribute("Что тут?");
        const char* target_id = edge->Attribute("Что тут?");
        if (!source_id || !target_id) continue;

        auto source_it = nodes.find(source_id);
        auto target_it = nodes.find(target_id);
        if (source_it == nodes.end() || target_it == nodes.end()) continue;

        string street_name;
        for (tinyxml2::XMLElement* data = edge->FirstChildElement("Что тут?"); data; data = data->NextSiblingElement("Что тут?")) {
            const char* key = data->Attribute("Что тут?");
            if (!key) continue;

            if (strcmp(key, "Что тут?8") == 0 && data->GetText()) { // street name
                street_name = utf8_to_cp1251(data->GetText());// нужно для преобразования кодировки
                // cout << "Улицы " << street_name << endl;
            }
        }

        edges.emplace_back(source_it->second, target_it->second, street_name);
    }

    cout << "Количество вершин " << nodes.size() << " ребер " << edges.size() << endl;

    return make_tuple(nodes, edges);
}

Как подсчитать расстояние?

Для расчёта расстояния между двумя точками на поверхности Земли часто используется формула гаверсинуса. Она позволяет вычислить кратчайшее расстояние между двумя точками, зная их координаты (широту и долготу), и часто применяется для вычислений на глобальной карте.

Формула гаверсинуса выглядит следующим образом:

a = sin²(Δφ/2) + cos(φ1) ⋅ cos(φ2) ⋅ sin²(Δλ/2)
c = 2 ⋅ atan2( √a, √(1−a) )
d = R ⋅ c

Где:

• φ1, φ2 — широты двух точек в радианах
• λ1, λ2 — долготы двух точек в радианах
• Δφ = φ2 − φ1 — разница широт
• Δλ = λ2 − λ1 — разница долгот
• R — радиус Земли (среднее значение 6,371 км)
• d — расстояние между двумя точками

Задание Реализуйте формулу.

PythonC++

def haversine(coord1: Tuple[float, float], coord2: Tuple[float, float]) -> float:
    """
    Вычисляет расстояние между двумя точками на поверхности Земли (в километрах)
    """
    lon1, lat1 = # что тут
    lon2, lat2 = # что тут
    R = 6371  # Радиус Земли в км

    phi1, phi2 = # что тут
    dphi = # что тут
    dlambda = # что тут

    a = # что тут
    return # что тут

typedef pair<double, double> Coord;
double haversine(const Coord& coord1, const Coord& coord2) {
// Вычисляем расстояние между точками на поверхности Земли (в километрах)
double lon1 = // что тут, lat1 = // что тут;
double lon2 = // что тут, lat2 = // что тут;
double R = 6371.0;  // Радиус Земли в км

double phi1 = // что тут;
double phi2 = // что тут;
// Альтернативный вариант расчёта углов:

phi1 = // что тут
phi2 = // что тут
double dphi = // что тут
double dlambda = // что тут

double a = // что тут
return // что тут
}

Почему использовать формулу гаверсинуса, а не евклидово расстояние?

Евклидово расстояние подходит для вычисления расстояний между точками на плоскости, где можно использовать прямолинейные расчёты. Однако Земля — это сфера (или, точнее, эллипсоид), и для точных вычислений на её поверхности необходимо учитывать кривизну.

Использование формулы гаверсинуса даёт более точные результаты при вычислении расстояний на поверхности Земли, так как она учитывает её сферическую форму. Евклидово расстояние не учитывает этой кривизны, что приводит к неточным результатам при больших расстояниях.

Для желающих продолжить*

Однажды братце Кролику приснился сон, в котором Цезаря окружило 3 сенаторов Гай Кассием Лонгино, Гай Требоний и Марк Юний Брут.
И последний сказал:

Пю кгфхгелп лёугхя хздв ес Iodssb elug жс жзфвхл сънсе! Ффюонг рг лёуц: kwwsv://udwfdwfkhu.ux/phgld/doj/sudfwlfh/sudf_10/elug.kwpo

Нфхгхл, тсъзпц хгп дзжю фс ыулчхсп? Ыулчх нсхсуюм лфтсоякцзхфв 04E_19__.WWI

Список использованных источников и благодарностей

1. (Algorithmica - open-access web book, автор Максим Иванов)[https://ru.algorithmica.org/cs/shortest-paths/dijkstra/]
2. (Алгоритмы на графах. Семинар 11. 18 апреля 2019 г.)[https://eduardgorbunov.github.io/assets/files/amc_778_seminar_11.pdf]
3. Иванов М. К. Алгоритмический тренинг. Решения практических задач на Python и C++. — СПб.: БХВ-Петербург, 2023. —416 с.: ил. ISBN 978-5-9775-1168-1