ДЗ Лабораторная работа №5 "Алгоритм поиска кратчайшего пути"#

Warning

За задание можно получить до 5 баллов, соблюдая следующие условия:
- Написано на C++ ( + 2 балла)
- Задание зачтено ( +3 балла)

В отчете должно быть указано следующие:
1. Титульный лист, где указаны ФИО преподавателя, номер задания, номер варианта
2. Формулировка задания
3. Ссылка на github-репозиторий с работающим кодом
4. Привести блок-схему и формулировку алгоритма Дейкстры
5. Для своего варианта произвести расчеты графа и приложить их
6. Показать граф для города по варианту. Указать количество вершин и количество ребер в графе
7. В конце работы приводятся реальные замеры на вашем ЭВМ в виде таблицы 1

Пример таблицы 1 "Расчет кратчайших путей для города {Ваш город}"

Пункт старта	Пункт назначения	Расстояние (км)	Рисунок (результат)	Время работы алгоритма
A	B	12.5	рисунок	0.23 с
B	C	8.1	рисунок	0.19 с
A	C	20.6	рисунок	0.35 с

Ход выполнения работы#

Подготовка графа дорог#

Независимо от того, планируете реализовывать в на С++ или Python произведите следующие действия:

1) установите на Python библиотеку osmnx с помощью команды pip install osmnx

2) Испльзуйте следующую команду для формирования файла с графами дорог (замените Моосква, Россия на город вашего варианта):

import osmnx as ox

# Скачиваем граф по названию города
G = ox.graph_from_place('Москва, Россия', network_type='drive')
# Сохраняем в файл для последующего использования
ox.save_graphml(G, 'moscow_road_network.graphml')

3) В дальнейшей работе мы будем использовать файл *.graphml для работы

Алгоритм Дейкстры#

Алгоритм Дейкстры — это метод поиска кратчайшего пути от одной вершины графа ко всем остальным. Он был разработан голландским учёным Эдсгером Дейкстрой в 1959 году.

В ориентированном взвешенном графе $G = (V, E)$ , вес рёбер которого неотрицателен и определяется весовой функцией $w: E \rightarrow \mathbb{R}$ , алгоритм Дейкстры находит длины кратчайших путей из заданной вершины $s$ до всех остальных.

В алгоритме поддерживается множество вершин $U$ , для которых уже вычислены длины кратчайших путей до них из $s$ .

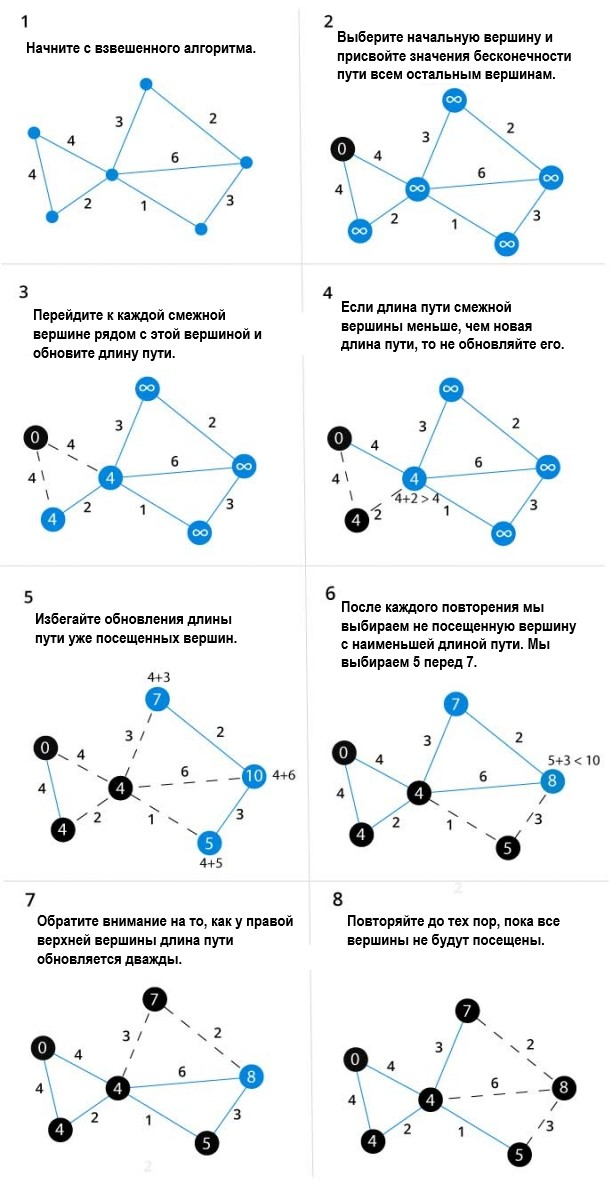
Шаг 1. Инициализируйте начальный узел с нулевой стоимостью, а остальную часть узла — с бесконечной стоимостью.

Шаг 2. Поддерживайте массив или список для отслеживания посещенных узлов.

Шаг 3. Обновите стоимость узла, указав минимальную стоимость. Это можно сделать путем сравнения текущей стоимости со стоимостью пути. (Демонстрация показана в разделе примеров)

Шаг 4. Продолжайте шаг 3, пока не будут посещены все узлы.

Игровое поле

function dijkstra(G, S)
    for each vertex V in G
        distance[V] <- infinite
        previous[V] <- NULL
        If V != S, add V to Priority Queue Q
    distance[S] <- 0

    while Q IS NOT EMPTY
        U <- Extract MIN from Q
        for each unvisited neighbour V of U
            tempDistance <- distance[U] + edge_weight(U, V)
            if tempDistance < distance[V]
                distance[V] <- tempDistance
                previous[V] <- U
    return distance[], previous[]

Игровое поле

Пример расчета Алгоритм Дейкстры#

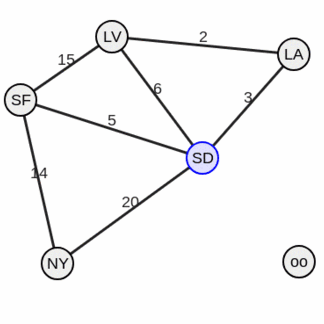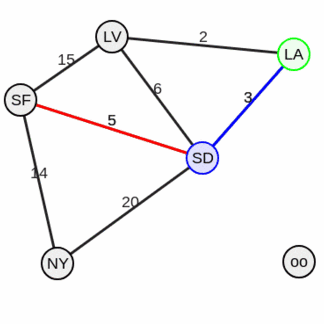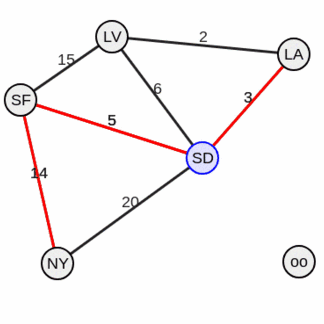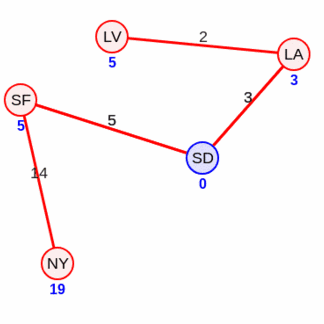
Пример гафа:

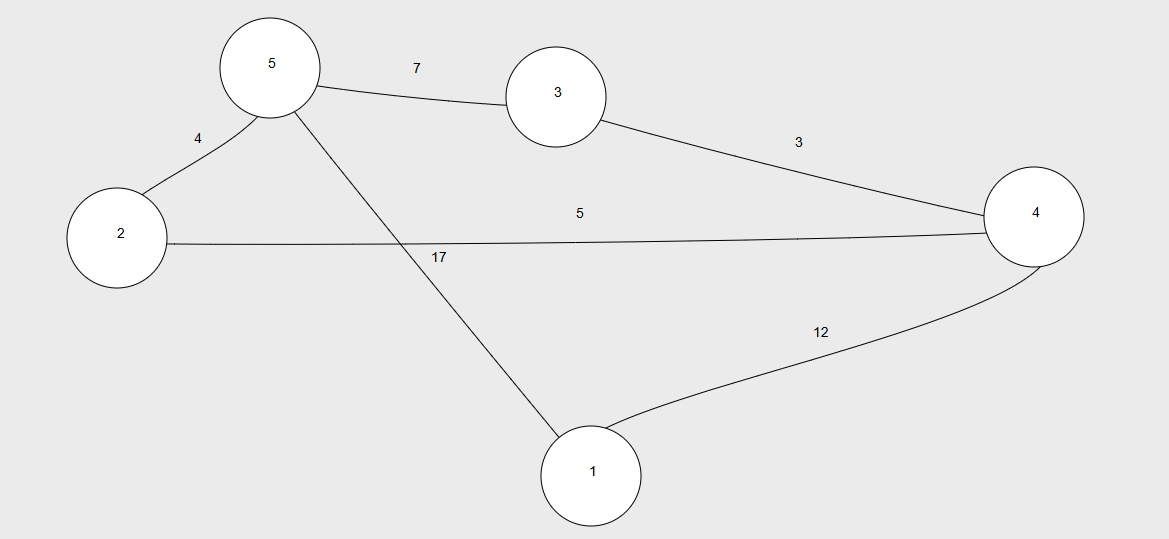
Игровое поле

Искать кратчайшее расстояние мы будем между вершинами 1 и 2

Матрица расстояний#

оставим матрицу расстояний по следующему правилу:
если между вершинами $i$ и $j$ есть ребро, то в ячейке $(i, j)$ записывается его вес,
если ребра нет — ставим символ бесконечности (обозначается как ∞).
Диагональные элементы (расстояние от вершины до самой себя) также равны 0.

	1	2	3	4	5
1	0	∞	∞	12	17
2	∞	0	∞	5	4
3	∞	∞	0	3	7
4	12	5	3	0	∞
5	17	4	7	∞	0

Шаг 1. Инициализация#

Устанавливаем расстояния D[i] от начальной вершины s = 1 до всех остальных:

D = [0, ∞, ∞, ∞, ∞]

То есть мы предполагаем, что расстояние до самой себя равно 0, а до остальных — бесконечность, потому что мы ещё не знаем пути к ним.
Создаём очередь с приоритетом, куда помещаем все вершины, начиная с s = 1.

Итерация №0#

Извлекаем вершину v = 1 (расстояние = 0).
Помещаем в множество посещённых H = {1}.
Обновляем расстояния для соседей v = 1:
D[2] = min(∞, 0 + 8) = 8
D[3] = min(∞, 0 + 17) = 17
D[4] = min(∞, 0 + 5) = 5
D[5] = min(∞, 0 + 4) = 4

D = [0, 8, 17, 5, 4]

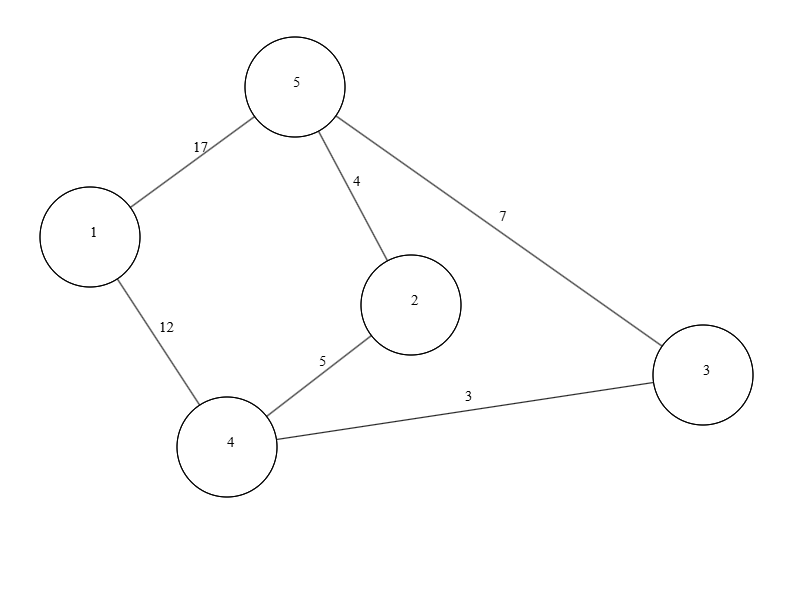
Игровое поле

Итерация №1#

Из очереди извлекаем вершину с минимальным расстоянием — v = 5 (4).
Добавляем её в H = {1, 5}.
Смотрим на её соседей:
D[2] = min(8, 4 + 7) = 8 (не меняется)
D[3] = min(17, 4 + 17) = 17 (не меняется)
D[4] = min(5, 4 + 9) = 5 (не меняется)

Поскольку все новые значения оказались не меньше текущих, значения в D не изменились.
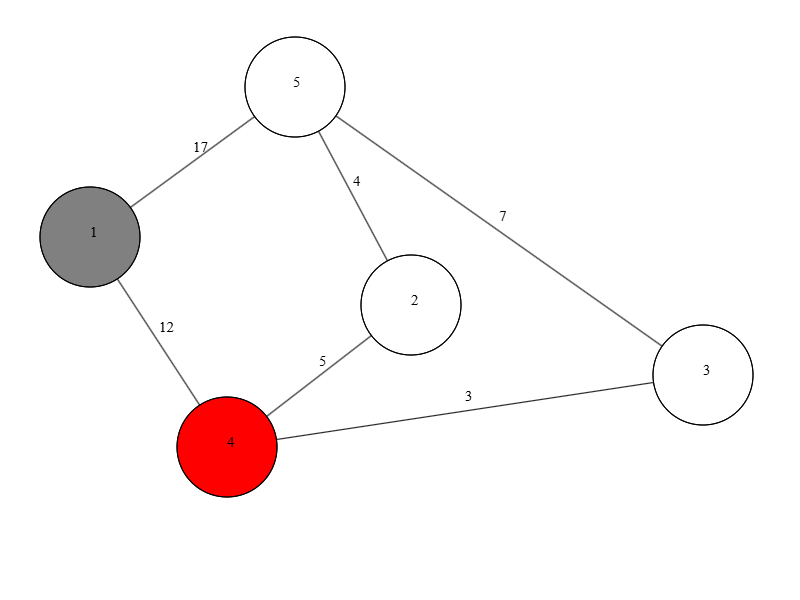
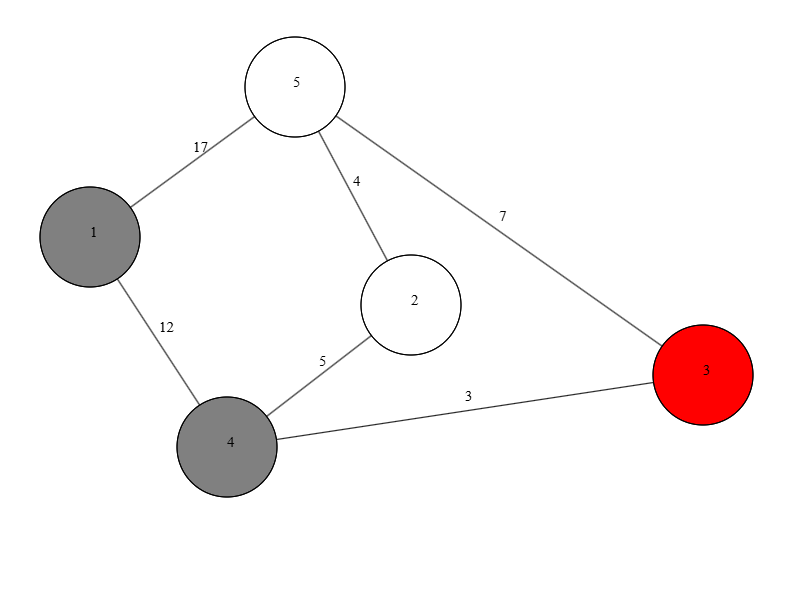
Игровое поле

Итерация №2#

Извлекаем вершину v = 4 (расстояние = 5).
H = {1, 5, 4}
Проверяем соседей:
D[2] = min(8, 5 + 3) = 8 (не меняется)
D[3] = min(17, 5 + 12) = 17 (не меняется)

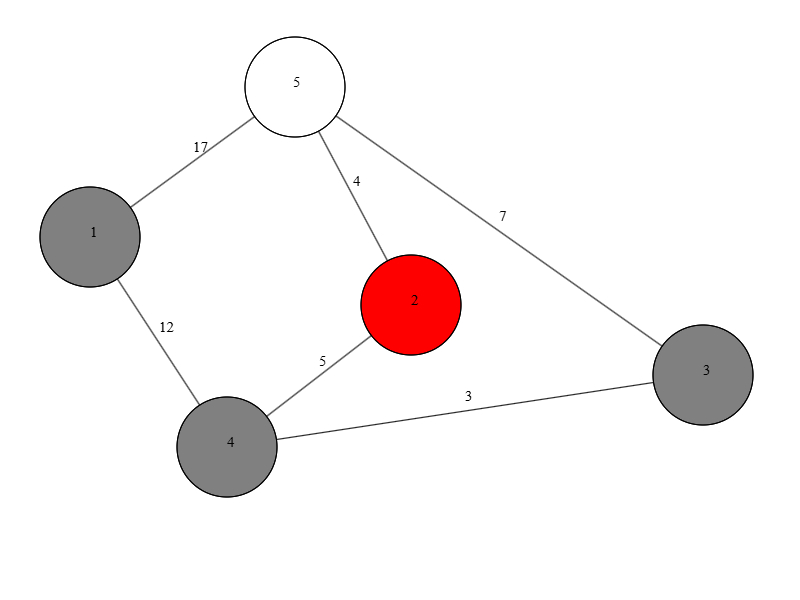
Игровое поле

Итерация №3#

Следующей извлекается вершина v = 2 (расстояние = 8).
H = {1, 5, 4, 2}
У неё сосед — v = 3:
D[3] = min(17, 8 + 15) = 17 (не меняется)

Игровое поле

Итерация №4#

Остаётся последняя вершина v = 3 (расстояние = 17).
Добавляем её в множество посещённых: H = {1, 2, 3, 4, 5}
Все вершины уже посещены — алгоритм завершён.

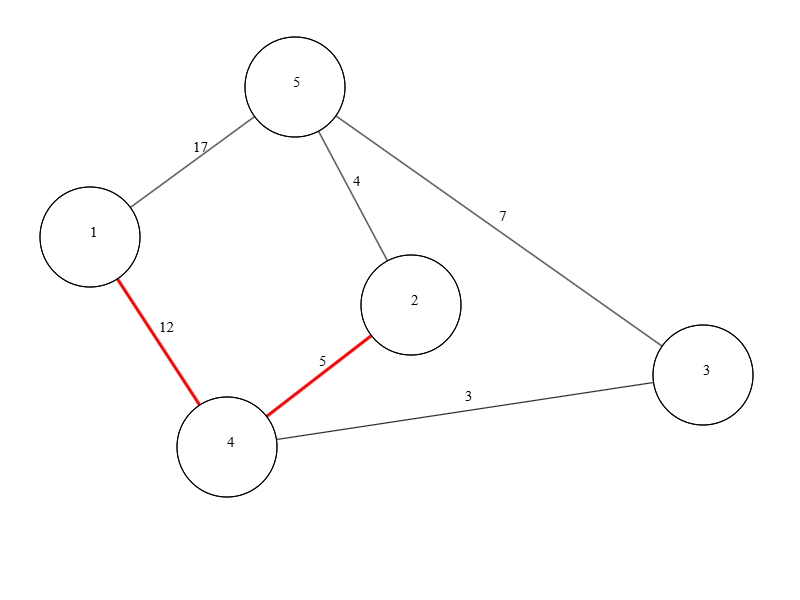
Игровое поле

Ответ#

Кратчайший путь от вершины 1 до вершины 2 можно восстановить, пройдя по "наиболее выгодным" рёбрам:
1 → 4 → 2

Длина пути: 5 (из 1 в 4) + 3 (из 4 в 2) = 8

Указания к реализации в коде#

Скачанные вами файл имеет формат GraphML

Tip

GraphML — язык описания графов, основанный на XML

Пример файла GraphML#

<?xml version="1.0" encoding="UTF-8"?>
<graphml xmlns="http://graphml.graphdrawing.org/xmlns"
         xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance"
         xsi:schemaLocation="http://graphml.graphdrawing.org/xmlns
                             http://graphml.graphdrawing.org/xmlns/1.0/graphml.xsd">

  <!-- Определения ключей (атрибутов) для данных -->
  <key id="d0" for="node" attr.name="label" attr.type="string"/>
  <key id="d1" for="edge" attr.name="weight" attr.type="double"/>

  <graph id="G" edgedefault="directed">
    <!-- Вершины -->
    <node id="n0">
      <data key="d0">A</data>
    </node>
    <node id="n1">
      <data key="d0">B</data>
    </node>
    <node id="n2">
      <data key="d0">C</data>
    </node>

    <!-- Рёбра -->
    <edge id="e0" source="n0" target="n1">
      <data key="d1">1.0</data>
    </edge>
    <edge id="e1" source="n1" target="n2">
      <data key="d1">2.0</data>
    </edge>
  </graph>
</graphml>

Корневой элемент <graphml> — содержит все данные в документе.

В нем задается пространство имен, которое указывает на спецификацию GraphML.

Элемент <key> — определяет атрибуты для рёбер и вершин. В этом примере:

d0 — атрибут для вершины, который будет хранить метку.
d1 — атрибут для рёбер, который будет хранить вес (число с плавающей точкой).

Элемент <graph> — сам граф, где:

id="G" — идентификатор графа.
edgedefault="directed" — граф ориентированный.

Вершины <node> — три вершины с уникальными идентификаторами n0, n1, n2, которые также могут содержать атрибуты, например, метку (label).

Рёбра <edge> — два рёбер:

Ребро с идентификатором e0 идет от вершины n0 к вершине n1 с весом 1.0.
Ребро с идентификатором e1 идет от вершины n1 к вершине n2 с весом 2.0.

Таким образом, нужно распарсить данную струткуру

Код python и C++#

PythonC++

Для визуализации на python будет использоваться бибилиотека matplotlib. Для парсинга файла xml.etree.ElementTree.

В коде сейчас есть функция для расчета расстония между точками haversine, функция построения графа build_graph, функция чтения из файла read_graphml, функции визхуализации и функции поиска id нужной вам улицы.

Вам осталось напишисать функцию dijkstra, которая реализует алгоритм Дейкстры для нахождения кратчайшего пути в графе. Функция должна принимать на вход граф, начальную и конечную вершины, а на выходе возвращать кратчайший путь, его длину и список названий улиц (если они имеются в графе).

Входные данные:

graph — граф, представленный в виде словаря. Ключами являются вершины графа (кортежи с координатами типа Tuple[float, float]), а значениями — списки смежных вершин, каждая из которых представлена кортежем вида (соседняя вершина, расстояние до неё). Пример:

start — начальная вершина в формате Tuple[float, float].

end — конечная вершина в формате Tuple[float, float].

Выходные данные:

path — список кортежей, представляющих кратчайший путь от начальной вершины до конечной, где каждая вершина — это кортеж с координатами.

total_distance — общее расстояние кратчайшего пути (тип float).

street_names — список названий улиц, которые были пройдены по пути (если информация о названиях улиц отсутствует в графе, вернуть пустой список).

  import xml.etree.ElementTree as ET
  import matplotlib.pyplot as plt
  from matplotlib.collections import LineCollection
  from typing import Dict, List, Tuple
  import math

  def haversine(coord1: Tuple[float, float], coord2: Tuple[float, float]) -> float:
      """
      Вычисляет расстояние между двумя точками на поверхности Земли (в километрах)
      """
      lon1, lat1 = coord1
      lon2, lat2 = coord2
      R = 6371  # Радиус Земли в км

      phi1, phi2 = math.radians(lat1), math.radians(lat2)
      dphi = math.radians(lat2 - lat1)
      dlambda = math.radians(lon2 - lon1)

      a = math.sin(dphi/2)**2 + math.cos(phi1)*math.cos(phi2)*math.sin(dlambda/2)**2
      return 2 * R * math.atan2(math.sqrt(a), math.sqrt(1 - a))

  import heapq

  def dijkstra(graph: Dict[Tuple[float, float], List[Tuple[Tuple[float, float], float]]],
              start: Tuple[float, float],
              end: Tuple[float, float]) -> Tuple[List[Tuple[float, float]], float, List[str]]:
      # Приоритетная очередь для хранения (расстояние, узел)
      # ВАШ КОД
      # Словарь для хранения кратчайшего расстояния до каждого узла и предыдущего узла
      # ВАШ КОД
      # Множество посещённых узлов
      # ВАШ КОД

      # ВАШ КОД

      # Восстановление пути
      # ВАШ КОД
      # Здесь не собираем названия улиц, так как их нет в графе, возвращаем пустой список
      # ВАШ КОД
      # ВАШ КОД
      # Реконструкция пути от конца к началу
      # ВАШ КОД
      # ВАШ КОД

      # Общее расстояние от начала до конца
      # ВАШ КОД

      return path, total_distance, street_names


  def build_graph(edges: List[Tuple[Tuple[float, float], Tuple[float, float], str]]) -> Dict[Tuple[float, float], List[Tuple[Tuple[float, float], float]]]:
      """
      Строит граф из рёбер
      """
      graph = {}
      for start, end, _ in edges:
          dist = haversine(start, end)
          graph.setdefault(start, []).append((end, dist))
          graph.setdefault(end, []).append((start, dist))  # если граф неориентированный
      return graph

  def read_graphml(file_path: str) -> Tuple[Dict[str, Tuple[float, float]], List[Tuple[Tuple[float, float], Tuple[float, float], str]]]:
      """
      Читает GraphML файл и возвращает узлы и ребра с названиями улиц

      Args:
          file_path: путь к файлу .graphml

      Returns:
          Кортеж (nodes, edges), где:
          - nodes: словарь {node_id: (x, y)}
          - edges: список [((x1, y1), (x2, y2), название_улицы), ...]
      """
      tree = ET.parse(file_path)
      root = tree.getroot()
      ns = {'g': 'http://graphml.graphdrawing.org/xmlns'}

      nodes = {}
      for node in root.findall('.//g:node', ns):
          node_id = node.get('id')
          x, y = None, None
          for data in node.findall('.//g:data', ns):
              if data.get('key') == 'd4':  # x координата (обычно longitude)
                  x = float(data.text)
              elif data.get('key') == 'd5':  # y координата (обычно latitude)
                  y = float(data.text)
          if x is not None and y is not None:
              nodes[node_id] = (x, y)

      edges = []
      for edge in root.findall('.//g:edge', ns):
          source = edge.get('source')
          target = edge.get('target')
          street_name = None

          for data in edge.findall('.//g:data', ns):
              if data.get('key') == 'd18':  # название улицы
                  street_name = data.text if data.text else None

          if source in nodes and target in nodes:
              edges.append((nodes[source], nodes[target], street_name))

      return nodes, edges

  def find_street_index(edges: List[Tuple[Tuple[float, float], Tuple[float, float], str]], 
                        street_name_query: str) -> Tuple[int, str]:
      """
      Возвращает индекс (номер) и название улицы по заданному имени

      Args:
          edges: список рёбер с названиями улиц
          street_name_query: название улицы для поиска

      Returns:
          Кортеж (индекс, название_улицы), если найдено, иначе (-1, None)
      """
      for i, (_, _, name) in enumerate(edges):
          if name and name.lower() == street_name_query.lower():
              return i, name
      return -1, None

  def visualize_path_with_network(nodes, edges, path, street_names=None, figsize=(20, 20)):
      """
      Визуализация всей дорожной сети + маршрута красным.
      Если передан список street_names, то названия улиц выводятся вдоль маршрута.
      """
      plt.figure(figsize=figsize)
      ax = plt.gca()

      # Все рёбра — серые
      all_lines = [(start, end) for start, end, _ in edges]
      lc = LineCollection(all_lines, linewidths=0.3, colors='gray', alpha=0.4)
      ax.add_collection(lc)

      # Путь — красный
      if path and len(path) > 1:
          path_lines = [(path[i], path[i+1]) for i in range(len(path)-1)]
          lc_path = LineCollection(path_lines, linewidths=2.0, colors='red', alpha=0.9)
          ax.add_collection(lc_path)

          # Отображаем названия улиц, если они заданы
          if street_names:
              for i in range(len(path)-1):
                  mid_point = ((path[i][0] + path[i+1][0]) / 2, (path[i][1] + path[i+1][1]) / 2)
                  if i < len(street_names) and street_names[i]:
                      plt.text(mid_point[0], mid_point[1], street_names[i],
                              fontsize=8, color='blue', ha='center')

      ax.autoscale()
      plt.axis('equal')
      plt.title('Кратчайший маршрут')
      plt.xlabel('Долгота')
      plt.ylabel('Широта')
      plt.grid(False)
      plt.tight_layout()
      plt.show()

  def save_visualization(filename: str, dpi: int = 300) -> None:
      """
      Сохраняет текущую визуализацию в файл

      Args:
          filename: имя файла для сохранения
          dpi: разрешение изображения
      """
      plt.savefig(filename, dpi=dpi, bbox_inches='tight')
      plt.close()


  def visualize_path_with_network(nodes, edges, path, street_names=None, figsize=(20, 20)):
      """
      Визуализация всей дорожной сети + маршрута красным.
      Если передан список street_names, то названия улиц выводятся вдоль маршрута.
      """
      plt.figure(figsize=figsize)
      ax = plt.gca()

      # Все рёбра — серые
      all_lines = [(start, end) for start, end, _ in edges]
      lc = LineCollection(all_lines, linewidths=0.3, colors='gray', alpha=0.4)
      ax.add_collection(lc)

      # Путь — красный
      if path and len(path) > 1:
          path_lines = [(path[i], path[i+1]) for i in range(len(path)-1)]
          lc_path = LineCollection(path_lines, linewidths=2.0, colors='red', alpha=0.9)
          ax.add_collection(lc_path)

          # Отображаем названия улиц, если они заданы
          if street_names:
              for i in range(len(path)-1):
                  mid_point = ((path[i][0] + path[i+1][0]) / 2, (path[i][1] + path[i+1][1]) / 2)
                  if i < len(street_names) and street_names[i]:
                      plt.text(mid_point[0], mid_point[1], street_names[i],
                              fontsize=8, color='blue', ha='center')

      ax.autoscale()
      plt.axis('equal')
      plt.title('Кратчайший маршрут')
      plt.xlabel('Долгота')
      plt.ylabel('Широта')
      plt.grid(False)
      plt.tight_layout()
      plt.show()

  def visualize_only_path(path, figsize=(10, 10)):
      """
      Визуализирует только маршрут (без остального графа)
      """
      if not path or len(path) < 2:
          print("Маршрут слишком короткий или отсутствует.")
          return

      plt.figure(figsize=figsize)
      ax = plt.gca()

      path_lines = [(path[i], path[i+1]) for i in range(len(path)-1)]
      lc_path = LineCollection(path_lines, linewidths=2.5, colors='red', alpha=0.9)
      ax.add_collection(lc_path)

      ax.autoscale()
      plt.axis('equal')
      plt.title("Кратчайший маршрут")
      plt.xlabel("Долгота")
      plt.ylabel("Широта")
      plt.grid(True)
      plt.tight_layout()
      plt.show()


  # Пример использования

  if __name__ == "__main__":
      # 1. Загрузка данных
      nodes, edges = read_graphml("moscow_road_network.graphml")

      # 2. Задаём названия улиц для начала и конца маршрута
      start_street_query = "Таганская улица"      # Название улицы для старта (пример)
      end_street_query = "улица Бунинская Аллея"      # Название улицы для финиша (пример)

      # 3. Используем find_street_index для определения нужных рёбер
      start_index, start_street = find_street_index(edges, start_street_query)
      end_index, end_street = find_street_index(edges, end_street_query)

      if start_index == -1 or end_index == -1:
          print("Не удалось найти заданную улицу для начала или конца маршрута")
      else:
          # 4. Определяем стартовый и конечный узлы:
          # Используем первую точку ребра для старта и вторую точку ребра для финиша.
          start_node = edges[start_index][0]
          end_node = edges[end_index][1]

          # 5. Строим граф и ищем кратчайший путь
          graph = build_graph(edges)
          path, distance, street_names = dijkstra(graph, start_node, end_node)

          if not path:
              print("Путь не найден")
          else:
              print(f"Найден путь длиной {distance:.2f} км")
              print("Улицы на пути:", ", ".join(filter(None, street_names)))

              # 6. Визуализация маршрута
              visualize_path_with_network(nodes, edges, path, street_names)

Для визуализации на C++ будет использоваться бибилиотека SFML. Для парсинга файла TinyXML2.

Скачать библиотеку TinyXML2 можно (тут)[https://disk.yandex.ru/d/CMjuEvbvogkltw] файлы TinyXML2.h и TinyXML3.cpp. Также там находится шрифт.

В работе по ООП мы стакливалсиь с бибилотекой TinyXML2, но на всякий случай напомню.

TinyXML2 — это простой, компактный и высокопроизводительный парсер XML, который можно легко интегрировать в другие программы.

просьба не впадать в панику от количества кода

Структура проекта (визуализация маршрутов по GraphML)

**Основные типы и структуры **:

Coord: координата узла (pair<double, double>).
EdgeItem: ребро графа с названием улицы (tuple<Coord, Coord, string>).
Graph: словарь соседей для каждой вершины (map<Coord, vector<pair<Coord, double>>>).

Основные функции
- read_graphml(file_path): загрузка узлов и рёбер из GraphML.
- build_graph(edges): создание графа из списка рёбер.
- dijkstra(graph, start, end): поиск кратчайшего пути алгоритмом Дейкстры.
- visualize_path_with_network(...): отображение сети и маршрута в окне SFML.
- haversine(coord1, coord2): вычисление расстояния между координатами на сфере (Земле).
- utf8_to_cp1251 / cp1251_to_utf8: перекодировка для работы с русскими названиями улиц.
- find_street_index(edges, name): поиск улицы по названию.

Ваша задача написать функцию dijkstra, используя следующие подсказки

Вход:
- graph: граф дорожной сети в виде списка смежности.
- start: начальная координата.
- end: конечная координата.

ВыходЖ
- Вектор координат, представляющий путь от start до end.
- Общее расстояние по кратчайшему пути.
- Вектор названий улиц вдоль маршрута (в данной реализации остаётся пустым, так как названия не извлекаются из графа).

Требования к реализации:
1. Использовать приоритетную очередь (std::priority_queue) для выбора узлов с минимальным расстоянием.
2. Хранить расстояния до узлов и их предшественников в словаре shortest_paths.
3. Обеспечить проверку уже посещённых узлов.
4. По завершении поиска восстановить путь, начиная с конечного узла, и вернуть его в правильном порядке.
5. Если путь не найден, вернуть пустой путь и бесконечное расстояние.

Дополнительно:
- Для хранения координат использовать тип Coord (обычно это pair<double, double>).
- При необходимости предусмотреть сравнение координат через оператор ==.
- Код должен быть читаемым и сопровожден комментариями, объясняющими ключевые шаги.

#include <SFML/Graphics.hpp>
#include <SFML/Window.hpp>
#include <SFML/System.hpp>
#include <iostream>
#include <fstream>
#include <sstream>
#include <cmath>
#include <map>
#include <vector>
#include <tuple>
#include <queue>
#include <limits>
#include <string>
#include <algorithm>
#include <windows.h>.

// TinyXML-2 dependency
#include "tinyxml2.h"

#ifndef M_PI
#define M_PI 3.14159265358979323846
#endif
// For convenience
using std::string;
using std::vector;
using std::map;
using std::tuple;
using std::pair;
using std::make_pair;
using std::make_tuple;
using std::cout;
using std::endl;

typedef pair<double, double> Coord;
typedef tuple<Coord, Coord, string> EdgeItem;
typedef map<Coord, vector<pair<Coord, double>>> Graph;

// Needed for using Coord as key in std::map. std::pair already has operator< defined.

// Функция haversine: вычисляет расстояние между двумя точками на поверхности Земли (в километрах)
double haversine(const Coord& coord1, const Coord& coord2) {
    // Вычисляем расстояние между точками на поверхности Земли (в километрах)
    double lon1 = coord1.first, lat1 = coord1.second;
    double lon2 = coord2.first, lat2 = coord2.second;
    double R = 6371.0;  // Радиус Земли в км

    double phi1 = std::atan2(std::sin(lat1 * M_PI / 180.0), std::cos(lat1 * M_PI / 180.0));
    double phi2 = std::atan2(std::sin(lat2 * M_PI / 180.0), std::cos(lat2 * M_PI / 180.0));
    // Альтернативный вариант расчёта углов:
    phi1 = lat1 * M_PI / 180.0;
    phi2 = lat2 * M_PI / 180.0;
    double dphi = (lat2 - lat1) * M_PI / 180.0;
    double dlambda = (lon2 - lon1) * M_PI / 180.0;

    double a = std::sin(dphi / 2.0) * std::sin(dphi / 2.0) +
        std::cos(phi1) * std::cos(phi2) *
        std::sin(dlambda / 2.0) * std::sin(dlambda / 2.0);
    return 2 * R * std::atan2(std::sqrt(a), std::sqrt(1 - a));
}

// Функция dijkstra: поиск кратчайшего пути в графе
// graph: Граф представленный в виде словаря: {координата: список {(соседняя координата, расстояние)}}
// start: стартовая координата
// end: конечная координата
// Возвращает кортеж (путь, общее расстояние, список названий улиц)
tuple<vector<Coord>, double, vector<string>> dijkstra(// ваш код тут // ) {
    // Приоритетная очередь для хранения (расстояние, узел)
    typedef pair<double, Coord> QueueItem;
    auto cmp = [](const QueueItem& left, const QueueItem& right) {
        return left.first > right.first;
        };
    std::priority_queue<QueueItem, vector<QueueItem>, decltype(cmp)> priority_queue(cmp);
    priority_queue.push(make_pair(0.0, start));

    // Словарь для хранения кратчайшего расстояния до каждого узла и предыдущего узла
    // ваш код
    // ваш код

    // Множество посещённых узлов
    // ваш код

    while (!priority_queue.empty()) {
        double current_distance = priority_queue.top().first;

        Coord current_node = // ваш код
        priority_queue.pop();

        // Если достигли конечного узла, прерываем поиск
        // ваш код

        // Если узел уже посещён, пропускаем
        if (std::find(visited.begin(), visited.end(), current_node) != visited.end()) {
            // ваш код
        }

        visited.push_back( // ваш код // );

        // Получаем список соседей, если он существует
        auto it = graph.find(current_node);
        if (it != graph.end()) {
            for (auto& neighbor_pair : it->second) {
                Coord neighbor = // ваш код 
                double distance = // ваш код 
                double total_distance = // ваш код 

                if (shortest_paths.find(neighbor) == shortest_paths.end() ||
                    total_distance < shortest_paths[neighbor].second) {
                    shortest_paths[neighbor] = make_pair(// ваш код );
                    priority_queue.push(make_pair(// ваш код ));
                }
            }
        }
    }

    // Восстановление пути
    vector<Coord> path;
    vector<string> street_names;
    if (shortest_paths.find(end) == shortest_paths.end()) {
        return make_tuple(path, std::numeric_limits<double>::infinity(), street_names);
    }

    // Реконструкция пути от конца к началу
    Coord current_node = end;
    while (true) {
        path.push_back(// ваш код );
        auto pred = shortest_paths[current_node].first;
        // Если предшественник равен (0,0) и расстояние равно 0, то это стартовый узел
        if (current_node == start)
            // ваш код 
        // ваш код 
    }
    std::reverse(path.begin(), path.end());

    // Общее расстояние от начала до конца
    double total_distance = shortest_paths[end].second;
    return make_tuple(path, total_distance, street_names);
}

// Функция build_graph: строит граф из рёбер
// edges: список рёбер формата ((x1, y1), (x2, y2), название_улицы)
Graph build_graph(const vector<EdgeItem>& edges) {
    // Строим граф
    Graph graph;
    for (const auto& edge : edges) {
        Coord start, end;
        string street;
        std::tie(start, end, street) = edge;
        double dist = haversine(start, end);
        graph[start].push_back(make_pair(end, dist));
        graph[end].push_back(make_pair(start, dist));  // если граф неориентированный
    }
    return graph;
}

// кодировка
std::string utf8_to_cp1251(const std::string& utf8_str) {
    int wide_len = MultiByteToWideChar(CP_UTF8, 0, utf8_str.c_str(), -1, nullptr, 0);
    std::wstring wide_str(wide_len, L'\0');
    MultiByteToWideChar(CP_UTF8, 0, utf8_str.c_str(), -1, &wide_str[0], wide_len);

    int cp1251_len = WideCharToMultiByte(1251, 0, wide_str.c_str(), -1, nullptr, 0, nullptr, nullptr);
    std::string cp1251_str(cp1251_len, '\0');
    WideCharToMultiByte(1251, 0, wide_str.c_str(), -1, &cp1251_str[0], cp1251_len, nullptr, nullptr);

    return cp1251_str;
}
// Функция read_graphml: читает GraphML файл и возвращает узлы и ребра с названиями улиц
// file_path: путь к файлу .graphml
// Возвращает кортеж (nodes, edges), где:
// - nodes: словарь {node_id: (x, y)}
// - edges: список [((x1, y1), (x2, y2), название_улицы), ...]


tuple<map<string, Coord>, vector<EdgeItem>> read_graphml(const string& file_path) {
    map<string, Coord> nodes;
    vector<EdgeItem> edges;
    SetConsoleCP(1251);
    SetConsoleOutputCP(1251);
    tinyxml2::XMLDocument doc;
    if (doc.LoadFile(file_path.c_str()) != tinyxml2::XML_SUCCESS) {
        std::cerr << "Error loading XML file: " << file_path << endl;
        return make_tuple(nodes, edges);
    }

    tinyxml2::XMLElement* graphml = doc.FirstChildElement("graphml");
    if (!graphml) {
        std::cerr << "Нет файла" << endl;
        return make_tuple(nodes, edges);
    }

    tinyxml2::XMLElement* graph = graphml->FirstChildElement("graph");
    if (!graph) {
        std::cerr << "Нет элементов графа" << endl;
        return make_tuple(nodes, edges);
    }


    for (tinyxml2::XMLElement* node = graph->FirstChildElement("node"); node; node = node->NextSiblingElement("node")) {
        const char* id = node->Attribute("id");
        if (!id) continue;

        double x = 0, y = 0;
        bool has_coords = false;

        for (tinyxml2::XMLElement* data = node->FirstChildElement("data"); data; data = data->NextSiblingElement("data")) {
            const char* key = data->Attribute("key");
            if (!key) continue;

            if (strcmp(key, "d5") == 0) { 
                x = atof(data->GetText());
                has_coords = true;
            }
            else if (strcmp(key, "d4") == 0) { 
                y = atof(data->GetText());
                has_coords = true;
            }
        }

        if (has_coords) {
            nodes[id] = make_pair(x, y);
        }
    }


    for (tinyxml2::XMLElement* edge = graph->FirstChildElement("edge"); edge; edge = edge->NextSiblingElement("edge")) {
        const char* source_id = edge->Attribute("source");
        const char* target_id = edge->Attribute("target");
        if (!source_id || !target_id) continue;

        auto source_it = nodes.find(source_id);
        auto target_it = nodes.find(target_id);
        if (source_it == nodes.end() || target_it == nodes.end()) continue;

        string street_name;
        for (tinyxml2::XMLElement* data = edge->FirstChildElement("data"); data; data = data->NextSiblingElement("data")) {
            const char* key = data->Attribute("key");
            if (!key) continue;

            if (strcmp(key, "d18") == 0 && data->GetText()) { // street name
                street_name = utf8_to_cp1251(data->GetText());// нужно для преобразования кодировки
                // cout << "Улицы " << street_name << endl;
            }
        }

        edges.emplace_back(source_it->second, target_it->second, street_name);
    }

    cout << "Количество вершин " << nodes.size() << " ребер " << edges.size() << endl;

    return make_tuple(nodes, edges);
}

std::string convert_cp1251_to_utf8(const std::string& input) {
    // 1. CP1251 → UTF-16 (Windows-1251 → wchar_t)
    int wlen = MultiByteToWideChar(1251, 0, input.c_str(), -1, nullptr, 0);
    if (wlen <= 0) return "";
    std::wstring wstr(wlen, L'\0');
    MultiByteToWideChar(1251, 0, input.c_str(), -1, &wstr[0], wlen);

    // 2. UTF-16 → UTF-8
    int ulen = WideCharToMultiByte(CP_UTF8, 0, wstr.c_str(), -1, nullptr, 0, nullptr, nullptr);
    if (ulen <= 0) return "";
    std::string utf8_str(ulen, '\0');
    WideCharToMultiByte(CP_UTF8, 0, wstr.c_str(), -1, &utf8_str[0], ulen, nullptr, nullptr);

    return utf8_str;
}

// Функция find_street_index: Возвращает индекс (номер) и название улицы по заданному имени
// edges: список рёбер с названиями улиц
// street_name_query: название улицы для поиска
// Возвращает кортеж (индекс, название_улицы), если найдено, иначе (-1, "")
pair<int, string> find_street_index(const vector<EdgeItem>& edges, const string& street_name_query) {
    for (size_t i = 0; i < edges.size(); i++) {
        Coord start, end;
        string name;
        std::tie(start, end, name) = edges[i];
        if (!name.empty()) {
            // Приводим к нижнему регистру для сравнения
            string lc_name = name, query = street_name_query;
            std::transform(lc_name.begin(), lc_name.end(), lc_name.begin(), ::tolower);
            std::transform(query.begin(), query.end(), query.begin(), ::tolower);
            if (convert_cp1251_to_utf8(lc_name) == convert_cp1251_to_utf8 (query)){
                return make_pair(static_cast<int>(i), name);
            }
        }
    }
    return make_pair(-1, "");
}

// Функция visualize_path_with_network: Визуализация всей дорожной сети + маршрута красным.
// Если передан список street_names, то названия улиц выводятся вдоль маршрута.
// Используется SFML для визуализации
void visualize_path_with_network(const map<string, Coord>& nodes,
    const vector<EdgeItem>& edges,
    const vector<Coord>& path,
    const vector<string>& street_names = vector<string>(),
    const sf::Vector2u& figsize = sf::Vector2u(800, 800)) {
    // Создаём окно с заданным размером
    sf::RenderWindow window(sf::VideoMode(figsize.x, figsize.y), "Кратчайший маршрут");

    // Определяем границы для масштабирования на основе всех координат
    double minX = std::numeric_limits<double>::max(), maxX = -std::numeric_limits<double>::max();
    double minY = std::numeric_limits<double>::max(), maxY = -std::numeric_limits<double>::max();
    // Обрабатываем узлы
    for (auto& node : nodes) {
        double x = node.second.first;
        double y = node.second.second;
        if (x < minX) minX = x;
        if (x > maxX) maxX = x;
        if (y < minY) minY = y;
        if (y > maxY) maxY = y;
    }
    // Функция для преобразования координат
    auto transform_coord = [=](const Coord& c) -> sf::Vector2f {
        double scaleX = (figsize.x - 40) / (maxX - minX + 1e-6);
        double scaleY = (figsize.y - 40) / (maxY - minY + 1e-6);
        float x = static_cast<float>((c.first - minX) * scaleX + 20);
        // Инвертируем y для графического отображения
        float y = static_cast<float>(figsize.y - ((c.second - minY) * scaleY + 20));
        return sf::Vector2f(x, y);
        };

    // Основной цикл окна
    while (window.isOpen()) {
        sf::Event event;
        while (window.pollEvent(event)) {
            if (event.type == sf::Event::Closed)
                window.close();
        }

        window.clear(sf::Color::White);

        // Рисуем все рёбра — серыми
        for (const auto& edge : edges) {
            Coord start, end;
            string dummy;
            std::tie(start, end, dummy) = edge;
            sf::Vertex line[] =
            {
                sf::Vertex(transform_coord(start), sf::Color(128,128,128)),
                sf::Vertex(transform_coord(end), sf::Color(128,128,128))
            };
            window.draw(line, 2, sf::Lines);
        }

        // Рисуем путь — красным
        if (!path.empty() && path.size() > 1) {
            for (size_t i = 0; i < path.size() - 1; i++) {
                sf::Vertex line[] =
                {
                    sf::Vertex(transform_coord(path[i]), sf::Color::Red),
                    sf::Vertex(transform_coord(path[i + 1]), sf::Color::Red)
                };
                window.draw(line, 2, sf::Lines);
                // Отображаем названия улиц, если они заданы
                if (!street_names.empty() && i < street_names.size() && !street_names[i].empty()) {
                    sf::Font font;
                    if (!font.loadFromFile("arial.ttf")) {
                        // Если шрифт не найден, пропускаем отображение названия
                    }
                    else {
                        sf::Text text;
                        text.setFont(font);
                        text.setString(street_names[i]);
                        text.setCharacterSize(12);
                        text.setFillColor(sf::Color::Blue);
                        // Вычисляем среднюю точку отрезка
                        float midX = (transform_coord(path[i]).x + transform_coord(path[i + 1]).x) / 2;
                        float midY = (transform_coord(path[i]).y + transform_coord(path[i + 1]).y) / 2;
                        text.setPosition(midX, midY);
                        window.draw(text);
                    }
                }
            }
        }

        window.display();
    }
}

// Дублированная функция visualize_path_with_network (идентичная предыдущей)
// В оригинальном коде функция была определена дважды, поэтому здесь она реализована с другим именем для избежания конфликта
void visualize_path_with_network_duplicate(const map<string, Coord>& nodes,
    const vector<EdgeItem>& edges,
    const vector<Coord>& path,
    const vector<string>& street_names = vector<string>(),
    const sf::Vector2u& figsize = sf::Vector2u(800, 800)) {
    // Вызов оригинальной функции, так как реализация идентична
    visualize_path_with_network(nodes, edges, path, street_names, figsize);
}

// Функция visualize_only_path: Визуализирует только маршрут (без остального графа)
void visualize_only_path(const vector<Coord>& path, const sf::Vector2u& figsize = sf::Vector2u(400, 400)) {
    if (path.empty() || path.size() < 2) {
        std::cout << "Маршрут слишком короткий или отсутствует." << std::endl;
        return;
    }

    // Создаём окно
    sf::RenderWindow window(sf::VideoMode(figsize.x, figsize.y), "Кратчайший маршрут (только путь)");

    // Определяем границы для масштабирования
    double minX = std::numeric_limits<double>::max(), maxX = -std::numeric_limits<double>::max();
    double minY = std::numeric_limits<double>::max(), maxY = -std::numeric_limits<double>::max();
    for (const auto& c : path) {
        if (c.first < minX) minX = c.first;
        if (c.first > maxX) maxX = c.first;
        if (c.second < minY) minY = c.second;
        if (c.second > maxY) maxY = c.second;
    }
    auto transform_coord = [=](const Coord& c) -> sf::Vector2f {
        double scaleX = (figsize.x - 40) / (maxX - minX + 1e-6);
        double scaleY = (figsize.y - 40) / (maxY - minY + 1e-6);
        float x = static_cast<float>((c.first - minX) * scaleX + 20);
        float y = static_cast<float>(figsize.y - ((c.second - minY) * scaleY + 20));
        return sf::Vector2f(x, y);
        };

    while (window.isOpen()) {
        sf::Event event;
        while (window.pollEvent(event))
            if (event.type == sf::Event::Closed)
                window.close();

        window.clear(sf::Color::White);

        // Рисуем путь красным
        for (size_t i = 0; i < path.size() - 1; i++) {
            sf::Vertex line[] =
            {
                sf::Vertex(transform_coord(path[i]), sf::Color::Red),
                sf::Vertex(transform_coord(path[i + 1]), sf::Color::Red)
            };
            window.draw(line, 2, sf::Lines);
        }

        window.display();
    }
}

// Функция save_visualization: Сохраняет текущую визуализацию в файл
// filename: имя файла для сохранения
// dpi: разрешение изображения (не используется в данном варианте, так как SFML сохраняет по пикселям)
void save_visualization(const string& filename, int dpi = 300) {
    // Используем RenderTexture для сохранения визуализации
    sf::RenderTexture renderTexture;
    sf::Vector2u size(800, 800);
    if (!renderTexture.create(size.x, size.y)) {
        std::cerr << "Не удалось создать RenderTexture" << std::endl;
        return;
    }
    renderTexture.clear(sf::Color::White);
    // Здесь не реализовано рисование, так как функция save_visualization
    // сохраняет текущую визуализацию, которая должна быть вызвана после завершения отрисовки.
    renderTexture.display();

    sf::Texture texture = renderTexture.getTexture();
    sf::Image screenshot = texture.copyToImage();
    if (!screenshot.saveToFile(filename)) {
        std::cerr << "Не удалось сохранить изображение в файл " << filename << std::endl;
    }
}
void print_edges(const std::vector<EdgeItem>& edges) {
    for (const auto& [start, end, name] : edges) {
        if (!name.empty()) {
            std::cout << "ул." << name;
        }
        std::cout << std::endl;
    }
}

// Основной блок использования
int main() {
    SetConsoleCP(1251);
    SetConsoleOutputCP(1251);
    // 1. Загрузка данных
    map<string, Coord> nodes;
    vector<EdgeItem> edges;
    std::tie(nodes, edges) = read_graphml("moscow_road_network.graphml");
  //  print_edges(edges);
    // 2. Задаём названия улиц для начала и конца маршрута
    Coord start, end;
    string name;
    std::tie(start, end, name) = edges[edges.size() - 1];
    string start_street_query = "Таганская улица";      // Название улицы для старта (пример)
    string end_street_query = "улица Бунинская Аллея";      // Название улицы для финиша (пример)

    // 3. Используем find_street_index для определения нужных рёбер
    pair<int, string> start_result = find_street_index(edges, start_street_query);
    std::cout << start_result.second << std::endl;
    pair<int, string> end_result = find_street_index(edges, end_street_query);
    std::cout << end_result.second << std::endl;
    int start_index = start_result.first;
    int end_index = end_result.first;
    string start_street = start_result.second;
    string end_street = end_result.second;

    if (start_index == -1 || end_index == -1) {
        std::cout << "Не удалось найти заданную улицу для начала или конца маршрута" << std::endl;
    }
    else {
        // 4. Определяем стартовый и конечный узлы:
        // Используем первую точку ребра для старта и вторую точку ребра для финиша.
        Coord start_node = std::get<0>(edges[start_index]);
        Coord end_node = std::get<1>(edges[end_index]);

        // 5. Строим граф и ищем кратчайший путь
        Graph graph = build_graph(edges);
        vector<Coord> path;
        double distance;
        vector<string> street_names;
        std::tie(path, distance, street_names) = dijkstra(graph, start_node, end_node);

        if (path.empty()) {
            std::cout << "Путь не найден" << std::endl;
        }
        else {
            std::cout << "Найден путь длиной " << distance << " км" << std::endl;
            std::cout << "Улицы на пути: ";
            bool first = true;
            for (const auto& s : street_names) {
                if (!s.empty()) {
                    if (!first)
                        std::cout << ", ";
                    std::cout << s;
                    first = false;
                }
            }
            std::cout << std::endl;

            // 6. Визуализация маршрута
            visualize_path_with_network(nodes, edges, path, street_names);
        }
    }

    return 0;
}

Варианты#

№	Граф (полный, A–B, A–C, ..., + маршрут)	Город, страна
1	A–B: 3, A–C: 5, A–D: 2, B–C: 4, B–D: 6, C–D: 1. Найти путь: A → C	Москва, Россия
2	A–B: 6, A–C: 2, A–D: 7, B–C: 3, B–D: 5, C–D: 4. Найти путь: B → D	Париж, Франция
3	A–B: 4, A–C: 3, A–D: 5, B–C: 2, B–D: 6, C–D: 1. Найти путь: A → D	Берлин, Германия
4	A–B: 2, A–C: 6, A–D: 4, B–C: 5, B–D: 3, C–D: 7. Найти путь: C → B	Рим, Италия
5	A–B: 7, A–C: 4, A–D: 6, B–C: 5, B–D: 2, C–D: 3. Найти путь: A → B	Мадрид, Испания
6	A–B: 1, A–C: 5, A–D: 3, B–C: 4, B–D: 6, C–D: 2. Найти путь: C → D	Лондон, Великобритания
7	A–B: 3, A–C: 6, A–D: 2, B–C: 1, B–D: 5, C–D: 4. Найти путь: B → C	Афины, Греция
8	A–B: 5, A–C: 2, A–D: 4, B–C: 3, B–D: 6, C–D: 1. Найти путь: D → A	Стокгольм, Швеция
9	A–B: 4, A–C: 3, A–D: 6, B–C: 2, B–D: 5, C–D: 1. Найти путь: A → B	Осло, Норвегия
10	A–B: 6, A–C: 5, A–D: 1, B–C: 2, B–D: 3, C–D: 4. Найти путь: C → A	Хельсинки, Финляндия
11	A–B: 2, A–C: 4, A–D: 5, B–C: 3, B–D: 6, C–D: 1. Найти путь: D → B	Варшава, Польша
12	A–B: 5, A–C: 1, A–D: 6, B–C: 2, B–D: 3, C–D: 4. Найти путь: A → D	Будапешт, Венгрия
13	A–B: 3, A–C: 6, A–D: 2, B–C: 5, B–D: 1, C–D: 4. Найти путь: B → A	Вена, Австрия
14	A–B: 4, A–C: 2, A–D: 3, B–C: 1, B–D: 5, C–D: 6. Найти путь: C → B	Прага, Чехия
15	A–B: 2, A–C: 6, A–D: 4, B–C: 3, B–D: 5, C–D: 1. Найти путь: B → D	Бухарест, Румыния
16	A–B: 6, A–C: 3, A–D: 5, B–C: 4, B–D: 1, C–D: 2. Найти путь: A → C	Загреб, Хорватия
17	A–B: 3, A–C: 5, A–D: 2, B–C: 6, B–D: 4, C–D: 1. Найти путь: C → A	Любляна, Словения
18	A–B: 1, A–C: 4, A–D: 6, B–C: 3, B–D: 2, C–D: 5. Найти путь: D → C	Белград, Сербия
19	A–B: 5, A–C: 3, A–D: 4, B–C: 2, B–D: 1, C–D: 6. Найти путь: A → D	Сараево, Босния
20	A–B: 2, A–C: 1, A–D: 6, B–C: 3, B–D: 5, C–D: 4. Найти путь: B → C	Скопье, Македония
21	A–B: 4, A–C: 2, A–D: 5, B–C: 3, B–D: 1, C–D: 6. Найти путь: A → B	Тирана, Албания
22	A–B: 6, A–C: 3, A–D: 4, B–C: 1, B–D: 5, C–D: 2. Найти путь: D → A	София, Болгария
23	A–B: 5, A–C: 2, A–D: 3, B–C: 6, B–D: 4, C–D: 1. Найти путь: C → D	Братислава, Словакия
24	A–B: 1, A–C: 4, A–D: 2, B–C: 3, B–D: 6, C–D: 5. Найти путь: A → C	Кишинёв, Молдова
25	A–B: 2, A–C: 3, A–D: 5, B–C: 6, B–D: 1, C–D: 4. Найти путь: D → B	Киев, Украина
26	A–B: 4, A–C: 5, A–D: 3, B–C: 2, B–D: 6, C–D: 1. Найти путь: B → A	Минск, Беларусь
27	A–B: 3, A–C: 2, A–D: 6, B–C: 4, B–D: 1, C–D: 5. Найти путь: C → A	Астана, Казахстан
28	A–B: 6, A–C: 4, A–D: 2, B–C: 1, B–D: 5, C–D: 3. Найти путь: A → D	Бишкек, Кыргызстан
29	A–B: 5, A–C: 3, A–D: 6, B–C: 2, B–D: 4, C–D: 1. Найти путь: B → C	Ташкент, Узбекистан
30	A–B: 1, A–C: 6, A–D: 4, B–C: 5, B–D: 2, C–D: 3. Найти путь: A → B	Ереван, Армения