Практика 9 Графы. Обход в ширину. Обход в глубину. Проверка связности.

Граф – совокупность точек, соединенных линиями.
- Точки называются вершинами (или узлами),
- Линии – ребрами (или дугами).

Note

Граф -  это множество вершин и ребер

Степень входа вершины – количество входящих в нее ребер.
Степень выхода – количество исходящих ребер.

Полный граф – граф, содержащий ребра между всеми парами вершин.

Взвешенный граф – граф, в котором ребрам поставлено в соответствие конкретное числовое значение.
- Это значение называется весом ребра.

Петля – ребро, у которого оба конца совпадают, то есть оно выходит и входит в одну и ту же вершину.

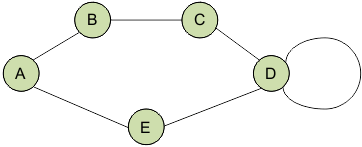
Классификация графов по кратности рёбер и наличию петель

Обыкновенный граф — структура, где между двумя вершинами может быть не более одного ребра, и петли отсутствуют.
Подходит для ситуаций, где важна единственная связь между элементами.
Пример: логистическая сеть с двусторонними дорогами, каждая пара точек соединена одним ребром.

Мультиграф — допускает кратные рёбра и петли.
Используется для моделирования систем с разными видами связей между одними и теми же вершинами.
Примеры:
- транспортные сети с автобусными, железнодорожными и авиамаршрутами;
- компьютерные сети с несколькими каналами связи.

Граф с петлями — разрешает наличие рёбер, соединяющих вершину саму с собой.
Актуален, если важно учитывать самоотношения.
Пример: рекомендательные системы, где петля означает повторное взаимодействие (например, повторная покупка).

Пустой граф — содержит только вершины, без рёбер.
Редко используется на практике, но важен в теоретических исследованиях.
Применяется для анализа крайних случаев и как отправная точка для построения других графов.

По связности:

• Связные графы – между любой парой вершин существует как минимум один путь.
• Несвязные графы – существует хотя бы одна вершина, не связанная с другими.

По направленности:

• Ориентированные графы – ребра направленные,
  переход возможен только в одном направлении между вершинами.

• Неориентированные графы – по ребрам возможен переход в обоих направлениях.

• Смешанные графы – содержат как ориентированные, так и неориентированные ребра.

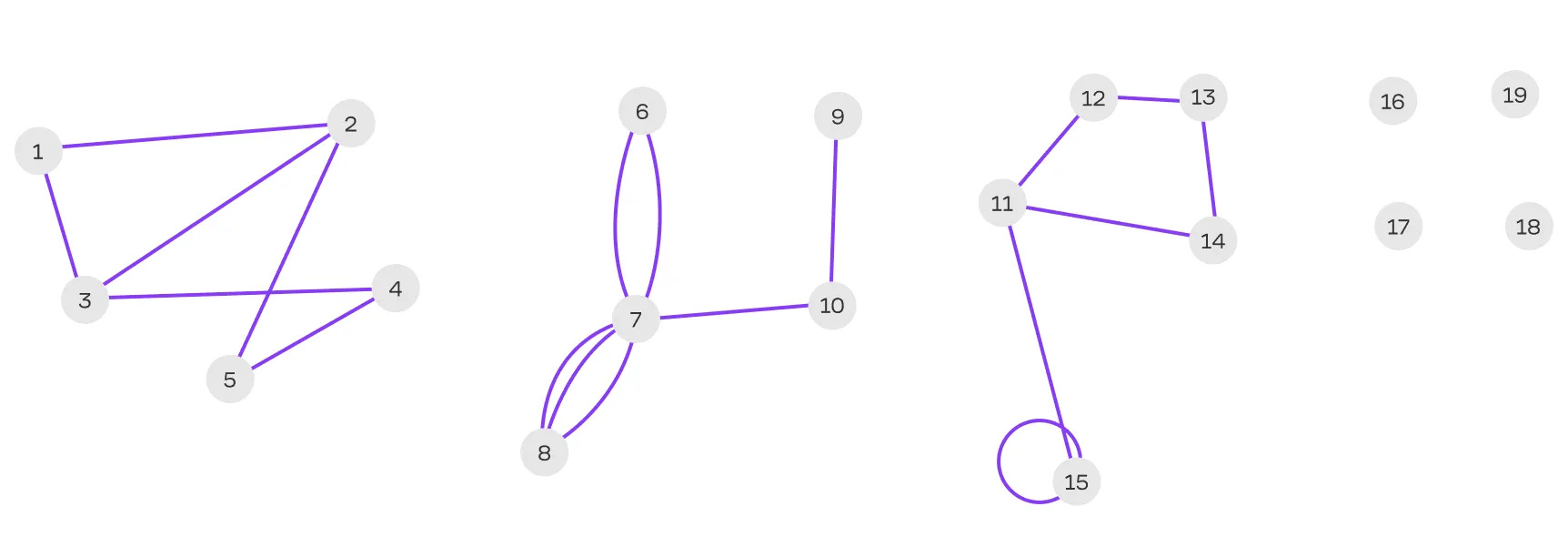
Направленность рёбер как характеристика графа

Неориентированный граф — граф, в котором рёбра не имеют направления.
Связь между вершинами — двусторонняя: если вершина A соединена с вершиной B, то и B соединена с A.

✅ Подходит для симметричных отношений, где взаимосвязи равноправны.
📌 Пример: социальный граф знакомств, в котором связь означает взаимное согласие на общение.

Ориентированный граф — граф, где каждое ребро имеет направление.
Если ребро направлено от A к B, это означает, что A связана с B, но не наоборот.

✅ Используется для моделирования односторонних взаимодействий.
📌 Пример: сюжетные линии в видеоиграх, где направление отражает выбор игрока.

Неориентированный граф можно представить как частный случай ориентированного,
в котором каждое ребро дублируется в обоих направлениях.

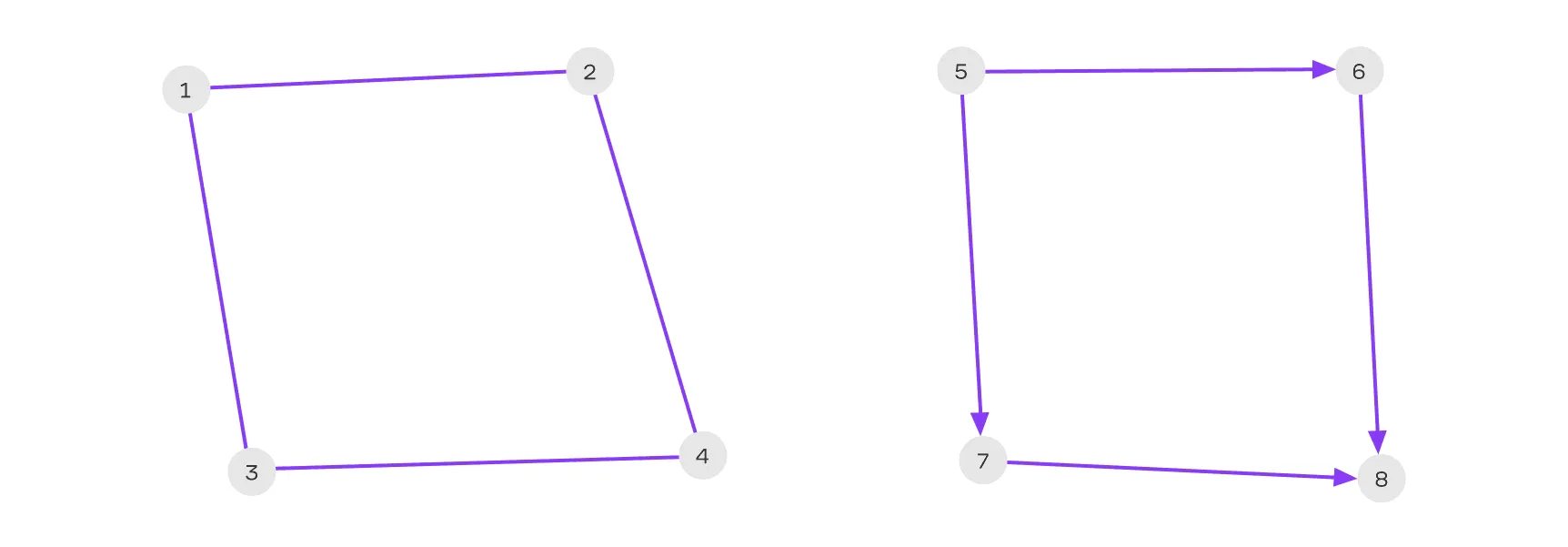
Связность графов

Связный неориентированный граф — из любой вершины можно добраться до любой другой по последовательности рёбер.
Граф образует единую компоненту связности.

✅ Применим в задачах, где все элементы должны быть взаимосвязаны.
📌 Пример: логистическая сеть города —
вершины — пункты доставки, рёбра — дороги.
Такой граф гарантирует, что груз можно доставить из любого города в любой другой.

---

Сильно связный ориентированный граф — из любой вершины можно попасть в любую другую, учитывая направление рёбер.

✅ Используется в моделях двустороннего обмена.
📌 Пример: внутренняя почтовая система организации —
вершины — сотрудники, рёбра — возможность отправить сообщение.
Сильная связность обеспечивает полную коммуникацию внутри структуры.

---

Слабо связный ориентированный граф — становится связным, если игнорировать направление рёбер.

✅ Подходит для анализа структуры односторонних связей.
📌 Пример: граф подписок в соцсетях —
вершины — пользователи, рёбра — подписки.
Даже если подписка односторонняя, можно изучать цепочки подписок и выявлять структурную связность.

⚠️ Однако слабая связность ≠ сильная связность —
достижимость всех вершин в обоих направлениях не гарантируется.

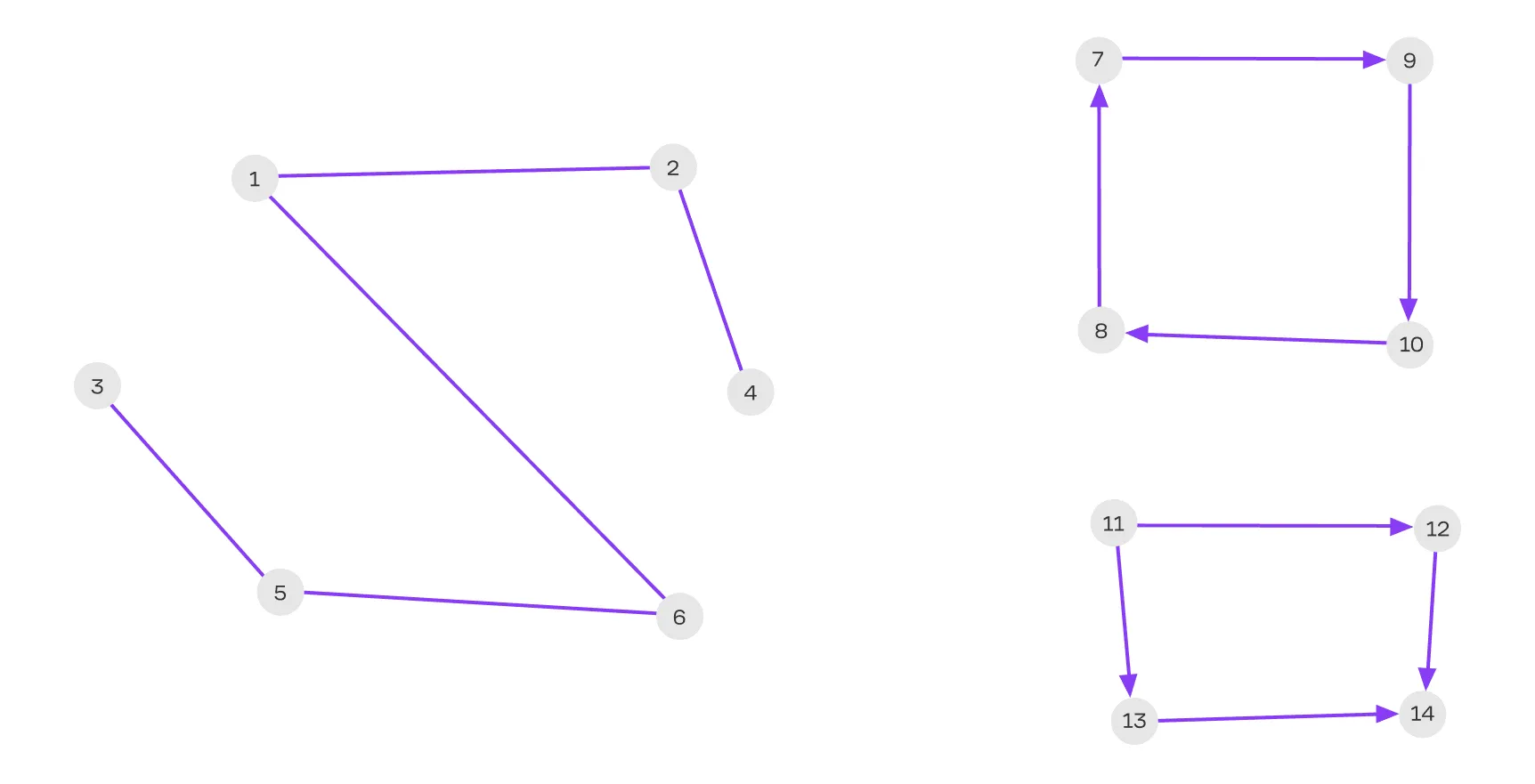
На иллюстрации выше:
Граф 1–6 — связный неориентированный.
Граф 7–10 — сильно связный ориентированный.
Граф 11–14 — слабо связный ориентированный.

Представление графов

Граф может быть представлен (сохранён) разными способами:

• Матрица смежности
• Матрица инцидентности
• Список смежности (инцидентности)
• Список рёбер

Матрица смежности и матрица инцидентности — представляют граф в виде двумерного массива (матрицы).
Размер такой матрицы зависит от количества вершин и/или рёбер в графе.

✅ Эти методы удобны для алгоритмов на матрицах и при необходимости быстрого доступа к информации о связях между вершинами.

Список рёбер

Список рёбер — это представление графа, в котором каждая строка описывает две смежные вершины и вес рёбер (для взвешенных графов).
Количество строк в списке рёбер соответствует общему количеству рёбер в графе:
- Для ориентированных рёбер — каждая пара рёбер считается отдельно.
- Для неориентированных рёбер — каждое ребро учитывается дважды (с обеих сторон).

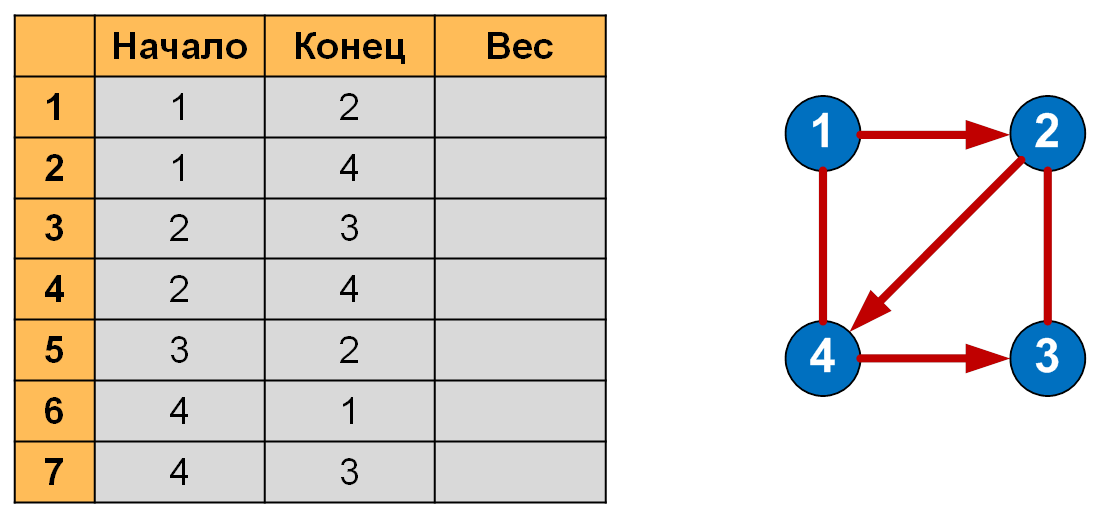
Пример для взвешенного графа:

Для графа с рёбрами A->B (вес 3) и B->C (вес 4) список рёбер будет выглядеть так:

(A, B, 3)
(B, C, 4)

Реализация Список рёбер

Рассмотрим реализацию в виде кода

PythonC++

# Ввод числа вершин и рёбер
vertex_count, edge_count = map(int, input("Введите количество вершин и рёбер (через пробел): ").split())

# Инициализация списка рёбер
edge_list = []

# Ввод рёбер и добавление их в список рёбер
print(f"Введите {edge_count} рёбер (по одному на строку, с номерами вершин):")
for _ in range(edge_count):
    vertex_from, vertex_to = map(int, input().split())

    # Добавляем ребро в список
    edge_list.append((vertex_from - 1, vertex_to - 1))  # Индексация с 1

# Вывод списка рёбер
print("\nСписок рёбер:")
for edge in edge_list:
    print(f"{edge[0] + 1} -> {edge[1] + 1}")  # Возвращаем индексацию к 1

#include <iostream>
#include <vector>

using namespace std;

int main() {
    int vertex_count, edge_count;

    // Ввод числа вершин и рёбер
    cout << "Введите количество вершин и рёбер (через пробел): ";
    cin >> vertex_count >> edge_count;

    // Инициализация списка рёбер
    vector<pair<int, int>> edge_list;

    // Ввод рёбер и добавление их в список рёбер
    cout << "Введите " << edge_count << " рёбер (по одному на строку, с номерами вершин):\n";
    for (int i = 0; i < edge_count; ++i) {
        int vertex_from, vertex_to;
        cin >> vertex_from >> vertex_to;

        // Уменьшаем индексы на 1, так как индексация вершин начинается с 1
        vertex_from -= 1;
        vertex_to -= 1;

        edge_list.push_back(make_pair(vertex_from, vertex_to));
    }

    // Вывод списка рёбер
    cout << "\nСписок рёбер:\n";
    for (const auto& edge : edge_list) {
        cout << edge.first + 1 << " -> " << edge.second + 1 << endl;  // Возвращаем индексацию к 1
    }

    return 0;
}

Список смежности (инцидентности)

Список смежности используется, когда количество рёбер графа относительно небольшое, и большинство элементов матрицы смежности равны 0. В таких случаях матрица смежности становится неэффективной, а использование списка смежности является более оптимальным.

По отношению к памяти список смежности менее требователен, чем матрица смежности. Он представляется в виде таблицы с двумя столбцами:
- Первый столбец: вершина, из которой выходят рёбра.
- Второй столбец: список вершин, в которые входят рёбра из текущей вершины.

Для взвешенных графов список смежности усложняется, так как каждый элемент списка должен содержать два значащих поля:
- Номер вершины, с которой соединяется текущая вершина.
- Вес ребра.

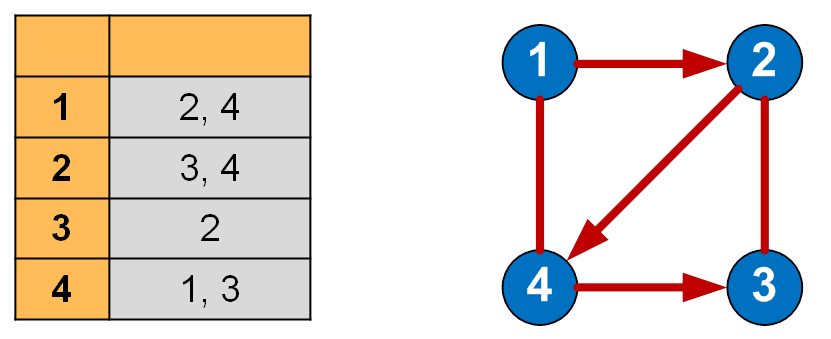
Пример: Для графа с вершинами A, B, C и рёбрами A->B и B->C список смежности будет выглядеть так:

A -> [B]
B -> [A, C]
C -> [B]

Здесь в первой строке указано, что из вершины A выходит ребро в вершину B, во второй — что из B выходят рёбра в A и C, а в третьей — что из C выходит ребро в B.

Преимущества списка смежности:
- Рациональное использование памяти.
- Быстрый перебор соседей вершины.
- Удобство проверки наличия рёбер и их удаления.

Недостатки списка смежности:
- При работе с насыщенными графами (где много рёбер) скорость может быть недостаточной.
- Нет быстрого способа проверить наличие ребра между двумя вершинами.
- Требуется заранее знать количество вершин графа.

Реализация Список смежности

PythonC++

# Ввод числа вершин и рёбер
vertex_count, edge_count = map(int, input("Введите количество вершин и рёбер (через пробел): ").split())

# Инициализация списка смежности
adj_list = [[] for _ in range(vertex_count)]

# Ввод рёбер и заполнение списка смежности
print(f"Введите {edge_count} рёбер (по одному на строку, с номерами вершин):")
for _ in range(edge_count):
    vertex_from, vertex_to = map(int, input().split())
    vertex_from -= 1
    vertex_to -= 1
    adj_list[vertex_from].append(vertex_to)

# Вывод списка смежности
print("\nСписок смежности:")
for i in range(vertex_count):
    print(f"Вершина {i + 1}: {adj_list[i]}")

#include <iostream>
#include <vector>

using namespace std;

int main() {
    int vertex_count, edge_count;

    // Ввод числа вершин и рёбер
    cout << "Введите количество вершин и рёбер (через пробел): ";
    cin >> vertex_count >> edge_count;

    // Инициализация списка смежности
    vector<vector<int>> adj_list(vertex_count);

    // Ввод рёбер и заполнение списка смежности
    cout << "Введите " << edge_count << " рёбер (по одному на строку, с номерами вершин):\n";
    for (int i = 0; i < edge_count; ++i) {
        int vertex_from, vertex_to;
        cin >> vertex_from >> vertex_to;

        // Уменьшаем индексы на 1, так как индексация вершин начинается с 1
        vertex_from -= 1;
        vertex_to -= 1;

        adj_list[vertex_from].push_back(vertex_to);
    }

    // Вывод списка смежности
    cout << "\nСписок смежности:\n";
    for (int i = 0; i < vertex_count; ++i) {
        cout << "Вершина " << i + 1 << ": ";
        for (int v : adj_list[i]) {
            cout << v + 1 << " ";  // Возвращаем индексацию к 1
        }
        cout << endl;
    }

    return 0;
}

Задание Выводите списки смежности в отсортированном виде для c++ используйте #include // Для использования функции sort, для python используйте sort (по умолчанию есть для list)

Матрица смежности

Матрица смежности — квадратная матрица, отображающая структуру графа.

• Количество строк и столбцов равно числу вершин графа.
• Значения элементов:
• 1 — между вершинами есть ребро;
• 0 — ребра нет.

Если из вершины A в вершину B есть ребро, то матрица[A][B] = 1.
Если граф не содержит петель, то элементы главной диагонали равны нулю.

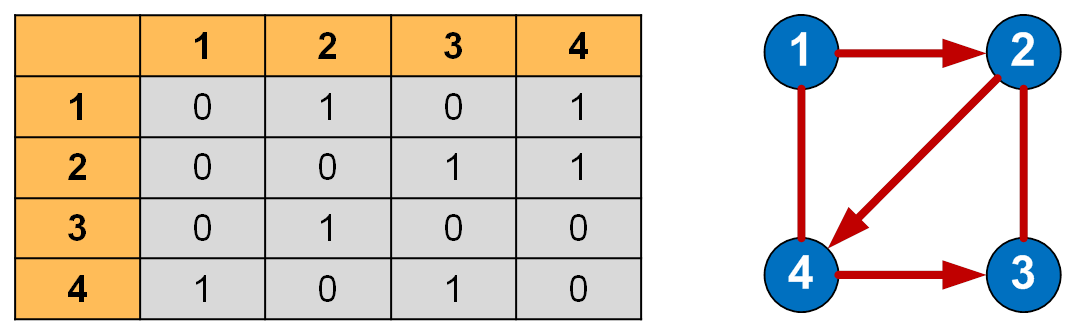
Пример

Граф с вершинами A, B, C и рёбрами между A–B и B–C:

   A B C
A [0 1 0]
B [1 0 1]
C [0 1 0]

В неориентированном графе матрица всегда симметрична относительно главной диагонали.

Наличие ребра или наличие пути?

Обратите внимание: матрица смежности определяется информацией о ребрах, а не о путях

Реализация матрицы смежности

Рассмотрим реализацию в виде кода (ориентированный граф)

PythonC++

# Ввод числа вершин и рёбер
V, E = map(int, input("Введите количество вершин и рёбер (через пробел): ").split())

# Инициализация матрицы смежности
adj_matrix = [[0] * V for _ in range(V)]

# Ввод рёбер и заполнение матрицы смежности
print("Введите рёбра (по одному на строку, с номерами вершин):")
for _ in range(E):
    u, v = map(int, input().split())
    adj_matrix[u - 1][v - 1] = 1  # Заполняем матрицу смежности для орграфа

# Вывод матрицы смежности
print("\nМатрица смежности:")
for row in adj_matrix:
    print(' '.join(map(str, row)))

#include <iostream>
#include <vector>
using namespace std;

int main() {
    int V, E;

    // Ввод числа вершин и рёбер
    cout << "Введите количество вершин и рёбер (через пробел): ";
    cin >> V >> E;

    // Инициализация матрицы смежности
    vector<vector<int>> adj_matrix(V, vector<int>(V, 0));

    // Ввод рёбер и заполнение матрицы смежности
    cout << "Введите рёбра (по одному на строку, с номерами вершин):" << endl;
    for (int i = 0; i < E; ++i) {
        int u, v;
        cin >> u >> v;
        adj_matrix[u - 1][v - 1] = 1;  // Заполняем матрицу смежности для орграфа
    }

    // Вывод матрицы смежности
    cout << "\nМатрица смежности:" << endl;
    for (int i = 0; i < V; ++i) {
        for (int j = 0; j < V; ++j) {
            cout << adj_matrix[i][j] << " ";
        }
        cout << endl;
    }

    return 0;
}

Задание : Проверьте работоспособность кода. Приведите изменения для неориентированных графов

Матрица инцидентности (инциденции) графа

Матрица инцидентности — матрица, в которой количество строк соответствует числу вершин, а количество столбцов — числу рёбер. В этой матрице указываются связи между инцидентными элементами графа (рёбрами и вершинами).

• В неориентированном графе:
• Если вершина инцидентна ребру, то соответствующий элемент матрицы равен 1;

• Если вершина не инцидентна ребру, то элемент равен 0.

• В ориентированном графе:

• Если ребро выходит из вершины, то элемент равен 1;
• Если ребро входит в вершину, то элемент равен -1;
• Если ребро отсутствует, то элемент равен 0.

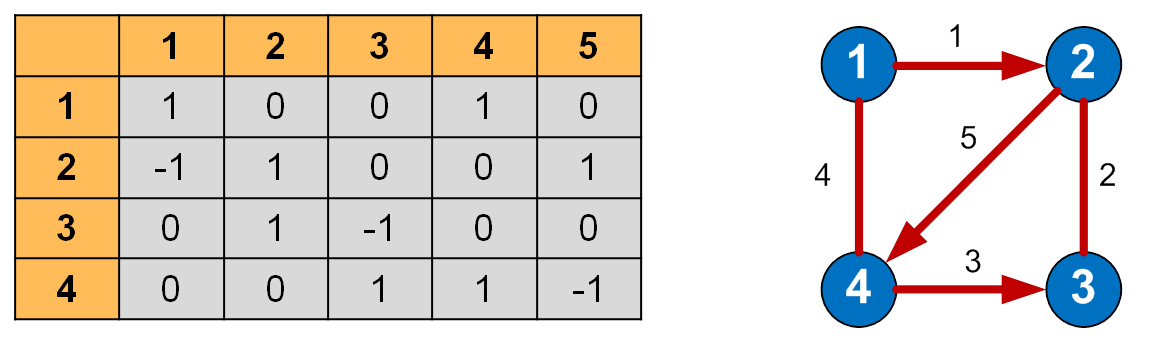
Пример:

Для ориентированного графа с вершинами A, B, C и рёбрами A->B и B->C, матрица инцидентности будет:

   A B C
1 [1 0 0]
2 [0 1 0]
3 [0 0 1]

Здесь:
- Строки — вершины (A, B, C),
- Столбцы — рёбра (A->B, B->C),
- В ячейках указано направление инцидентности.

Примечание: Для представления матрицы инцидентности требуется нумерация рёбер, что может быть неудобно в некоторых случаях.

Рассмотрим реализацию в виде кода

PythonC++

# Ввод числа вершин и рёбер
vertex_count, edge_count = map(int, input("Введите количество вершин и рёбер (через пробел): ").split())

# Инициализация матрицы инцидентности
# Матрица размера vertex_count x edge_count, все элементы изначально равны 0
inc_matrix = [[0] * edge_count for _ in range(vertex_count)]

# Ввод рёбер и заполнение матрицы инцидентности
print(f"Введите {edge_count} рёбер (по одному на строку, с номерами вершин):")
for i in range(edge_count):
    vertex_from, vertex_to = map(int, input().split())
    vertex_from -= 1  # Приводим к индексации с 0
    vertex_to -= 1    # Приводим к индексации с 0

    # Для ориентированного графа, инцидентность:
    # - 1 для вершины, из которой выходит ребро
    # - -1 для вершины, в которую входит ребро
    inc_matrix[vertex_from][i] = 1
    inc_matrix[vertex_to][i] = -1

# Вывод матрицы инцидентности
print("\nМатрица инцидентности:")
for row in inc_matrix:
    print(' '.join(map(str, row)))

#include <iostream>
#include <vector>

using namespace std;

int main() {
    int vertex_count, edge_count;

    // Ввод числа вершин и рёбер
    cout << "Введите количество вершин и рёбер (через пробел): ";
    cin >> vertex_count >> edge_count;

    // Инициализация матрицы инцидентности
    // Матрица размера vertex_count x edge_count, все элементы изначально равны 0
    vector<vector<int>> inc_matrix(vertex_count, vector<int>(edge_count, 0));

    // Ввод рёбер и заполнение матрицы инцидентности
    cout << "Введите " << edge_count << " рёбер (по одному на строку, с номерами вершин):" << endl;
    for (int i = 0; i < edge_count; ++i) {
        int vertex_from, vertex_to;
        cin >> vertex_from >> vertex_to;

        // Приводим к индексации с 0
        vertex_from -= 1;
        vertex_to -= 1;

        // Для ориентированного графа, инцидентность:
        // - 1 для вершины, из которой выходит ребро
        // - -1 для вершины, в которую входит ребро
        inc_matrix[vertex_from][i] = 1;
        inc_matrix[vertex_to][i] = -1;
    }

    // Вывод матрицы инцидентности
    cout << "\nМатрица инцидентности:" << endl;
    for (const auto& row : inc_matrix) {
        for (int val : row) {
            cout << val << " ";
        }
        cout << endl;
    }

    return 0;
}

Разница между матрицей смежности и списком смежности

Параметр	Матрица смежности	Список смежности
Использование памяти	Требует O(V^2) памяти	Требует O(V + E) памяти
Запрос на существование рёбер	Быстрая проверка O(1)	Проверка O(степени(v)) для соседей вершины v
Эффективность по памяти	Неэффективен для разрежённых графов	Эффективен для разрежённых графов
Добавление/удаление рёбер	O(1) для добавления/удаления рёбер	Зависит от структуры данных, обычно O(1)
Итерация по рёбрам	Неэффективно, возможно O(V^2) при обходе	Эффективно, O(V + E) при обходе
Подходящий для	Подходит для плотных графов	Подходит для разрежённых графов

Заметки о выборе метода представления графа

Выбор метода представления графа зависит от отношения между числом вершин и числом рёбер. Графы могут быть:
- Плотными (с большим количеством рёбер);
- Разреженными (с малым количеством рёбер).

• Плотные графы (где количество рёбер близко к максимальному) удобнее хранить в матрице смежности.
• Разрежённые графы (где количество рёбер значительно меньше количества вершин) лучше хранить в списке смежности.

Этот выбор зависит от структуры графа и того, какие операции должны быть выполнены с графом. Например, для быстрого поиска всех соседей вершины удобнее использовать список смежности, а для эффективных операций с рёбрами и проверок наличия рёбер между вершинами — матрицу смежности.

Алгоритмы обхода графов

Основными алгоритмами обхода графов являются:
- Поиск в глубину
- Поиск в ширину

Поиск в глубину

Обход в глубину (DFS) — один из самых простых алгоритмов обхода графа. Входными параметрами для него являются граф и стартовая вершина. Алгоритм заключается в следующем:

1. Перебираем все рёбра, исходящие из стартовой вершины, и рекурсивно запускаем себя из каждой.
2. По окончании работы алгоритм обойдёт все вершины и рёбра, достижимые из стартовой вершины.
3. Ключевая деталь, делающая этот алгоритм быстрым, — пропуск уже посещённых вершин. Для этого вводится дополнительный массив из n булевых переменных, в которых хранится информация о том, посещал ли обход в глубину каждую вершину или нет.
4. Рекурсивные запуски будем производить только из тех вершин, которые ещё не помечены как посещённые.

Время работы алгоритма обхода в глубину зависит от способа представления графа. Однако важно отметить, что обход в глубину посещает каждую вершину не более одного раза, и при каждом посещении просматривает список исходящих рёбер только один раз.

Рассмотрим иллюстрацию:
Каждая вершина может находиться в одном из 3 состояний:

0 — оранжевый – необнаруженная вершина;
1 — зеленый – обнаруженная, но не посещенная вершина;
2 — серый – обработанная вершина;
Фиолетовый – рассматриваемая вершина.

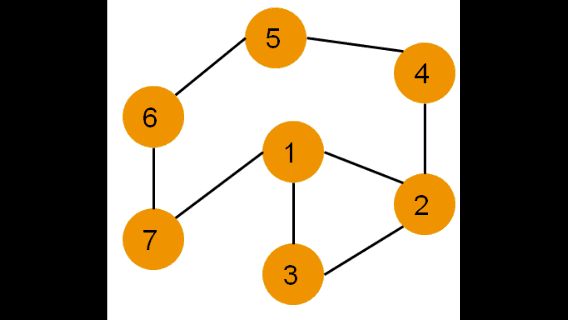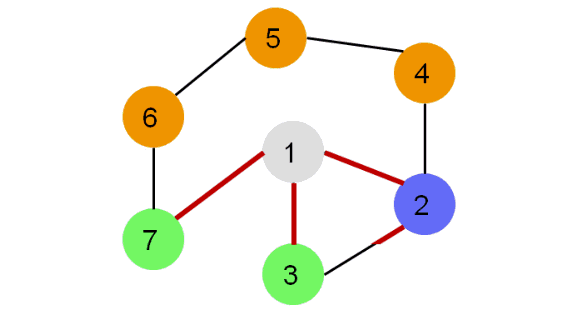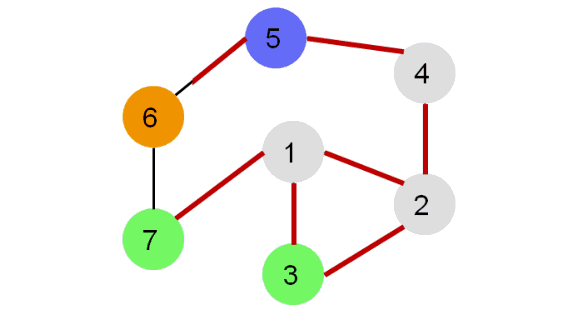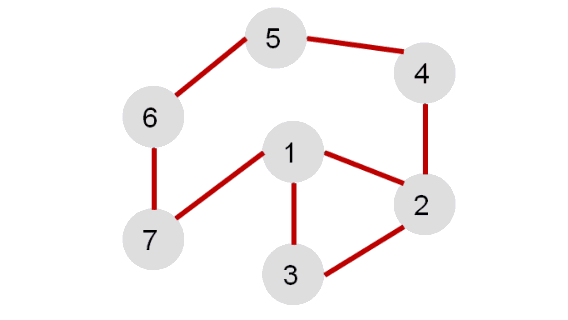
Для реализации алгоритма удобно использовать стек или рекурсию.

Реализация поиска в глубину

Обход в глубину на матрице смежности

PythonC++

def dfs(vertex):
    visited[vertex] = True  # Помечаем вершину как посещённую
    for to in range(vertex_count):  # Перебираем все вершины
        # Если есть ребро между текущей вершиной и вершиной to, и вершина to ещё не посещена
        if adj_matr[vertex][to] and not visited[to]:
            dfs(to)  # Рекурсивно вызываем dfs для вершины to

# Чтение количества вершин и рёбер
vertex_count, edge_count = map(int, input("Введите количество вершин и рёбер: ").split())

# Инициализация матрицы смежности
adj_matr = [[False] * vertex_count for _ in range(vertex_count)]

# Ввод рёбер и заполнение матрицы смежности
print("Введите рёбра (по одному на строку, с номерами вершин):")
for _ in range(edge_count):
    u, v = map(int, input().split())
    u -= 1  # Индексация с 0
    v -= 1  # Индексация с 0
    adj_matr[u][v] = True  # Заполняем матрицу смежности

# Массив для отслеживания посещённых вершин
visited = [False] * vertex_count

# Запуск DFS начиная с вершины 0 (вершина №1)
dfs(0)

# Вывод результатов
print("Вершины, которые были посещены:")
print(visited)  

#include <iostream>
#include <vector>

using namespace std;

// Рекурсивная функция для обхода в глубину
void dfs(int vertex, vector<vector<bool>>& adj_matr, vector<bool>& visited) {
    visited[vertex] = true;  // Помечаем вершину как посещённую
    for (int to = 0; to < adj_matr.size(); ++to) {  // Перебираем все вершины
        // Если есть ребро между текущей вершиной и вершиной to, и вершина to ещё не посещена
        if (adj_matr[vertex][to] && !visited[to]) {
            dfs(to, adj_matr, visited);  // Рекурсивно вызываем dfs для вершины to
        }
    }
}

int main() {
    int vertex_count, edge_count;

    // Чтение количества вершин и рёбер
    cout << "Введите количество вершин и рёбер: ";
    cin >> vertex_count >> edge_count;

    // Инициализация матрицы смежности
    vector<vector<bool>> adj_matr(vertex_count, vector<bool>(vertex_count, false));

    // Ввод рёбер и заполнение матрицы смежности
    cout << "Введите рёбра (по одному на строку, с номерами вершин):\n";
    for (int i = 0; i < edge_count; ++i) {
        int u, v;
        cin >> u >> v;
        u -= 1;  // Индексация с 0
        v -= 1;  // Индексация с 0
        adj_matr[u][v] = true;  // Заполняем матрицу смежности
    }

    // Массив для отслеживания посещённых вершин
    vector<bool> visited(vertex_count, false);

    // Запуск DFS начиная с вершины 0 (вершина №1)
    dfs(0, adj_matr, visited);

    // Вывод результатов
    cout << "Вершины, которые были посещены:\n";
    for (bool v : visited) {
        cout << (v ? "1" : "0") << " ";
    }
    cout << endl;

    return 0;
}

Обход в глубину на списках смежности

PythonC++

def dfs(vertex):
    visited[vertex] = True  # Помечаем вершину как посещённую
    for to in adj_list[vertex]:  # Перебираем соседей вершины
        if not visited[to]:  # Если сосед не посещён
            dfs(to)  # Рекурсивно вызываем dfs для этого соседа

# Чтение количества вершин и рёбер
vertex_count, edge_count = map(int, input("Введите количество вершин и рёбер: ").split())

# Инициализация списка смежности
adj_list = [[] for _ in range(vertex_count)]

# Ввод рёбер и заполнение списка смежности
print("Введите рёбра (по одному на строку, с номерами вершин):")
for _ in range(edge_count):
    u, v = map(int, input().split())
    u -= 1  # Индексация с 0
    v -= 1  # Индексация с 0
    adj_list[u].append(v)  # Добавляем ребро в список смежности

# Массив для отслеживания посещённых вершин
visited = [False] * vertex_count

# Запуск DFS начиная с вершины 0 (вершина №1)
dfs(0)

# Вывод результатов
print("Вершины, которые были посещены:")
print(visited)

#include <iostream>
#include <vector>

using namespace std;

// Функция для выполнения обхода в глубину
void dfs(int vertex, vector<bool>& visited, const vector<vector<int>>& adj_list) {
    visited[vertex] = true;  // Помечаем вершину как посещённую
    for (int to : adj_list[vertex]) {  // Перебираем соседей вершины
        if (!visited[to]) {  // Если сосед не посещён
            dfs(to, visited, adj_list);  // Рекурсивно вызываем dfs для этого соседа
        }
    }
}

int main() {
    int vertex_count, edge_count;

    // Чтение числа вершин и рёбер
    cout << "Введите количество вершин и рёбер: ";
    cin >> vertex_count >> edge_count;

    // Инициализация списка смежности
    vector<vector<int>> adj_list(vertex_count);

    // Ввод рёбер и заполнение списка смежности
    cout << "Введите рёбра (по одному на строку, с номерами вершин):\n";
    for (int i = 0; i < edge_count; ++i) {
        int u, v;
        cin >> u >> v;
        u -= 1;  // Индексация с 0
        v -= 1;  // Индексация с 0
        adj_list[u].push_back(v);  // Добавляем ребро в список смежности
    }

    // Массив для отслеживания посещённых вершин
    vector<bool> visited(vertex_count, false);

    // Запуск DFS начиная с вершины 0 (вершина №1)
    dfs(0, visited, adj_list);

    // Вывод результатов
    cout << "Вершины, которые были посещены:\n";
    for (bool is_visited : visited) {
        cout << is_visited << " ";
    }
    cout << endl;

    return 0;
}

Ограничение на глубину рекурсии

Обход в глубину (DFS) требует значительных ресурсов стека из-за рекурсивных вызовов. 
В худшем случае, если граф связан, глубина рекурсии может достичь числа вершин. В задачах с большим количеством вершин (сотни тысяч) это может привести к переполнению стека и аварийному завершению программы. 
В C++ с компилятором MSVC можно увеличить размер стека с помощью директивы #pragma, но в других случаях требуется использовать флаги тестирующей системы. В Python увеличение стека напрямую невозможно, что ограничивает использование DFS для больших графов.

Задание : Определите одинаковое ли время работы алгоритма обхода в глубину на списке смежности и матрицы смежности?

Поиск в ширину

Алгоритм обхода в ширину (англ. breadth-first search, или, сокращенно, BFS) действует таким образом, что он постепенно удаляется от стартовой вершины, двигаясь от неё по всевозможным направлениям.

Поиск в ширину (BFS) подразумевает поуровневое исследование графа:

1. Вначале посещается корень – произвольно выбранный узел.
2. Затем посещаются все потомки данного узла.
3. После этого посещаются потомки потомков и т.д.
4. Вершины просматриваются в порядке возрастания их расстояния от корня.
5. Алгоритм прекращает свою работу после обхода всех вершин графа или в случае выполнения требуемого условия (например, найти кратчайший путь из вершины 1 в вершину 6).

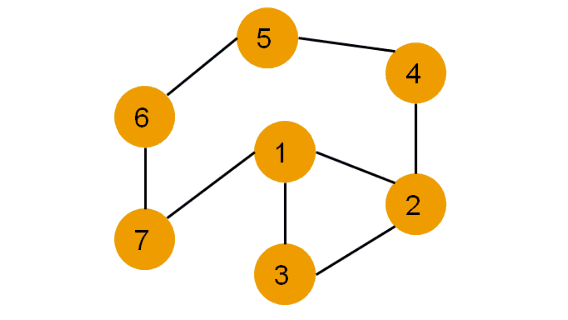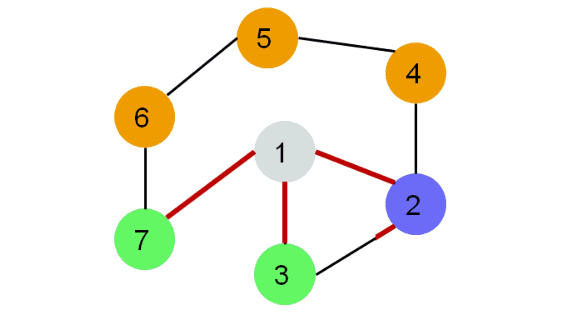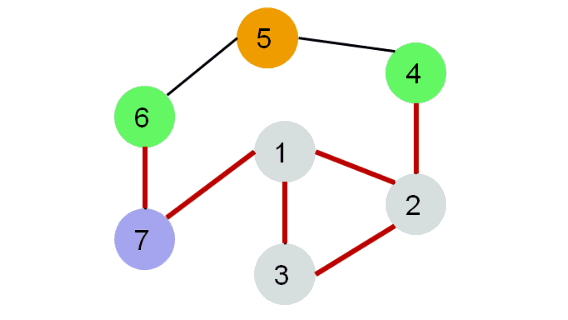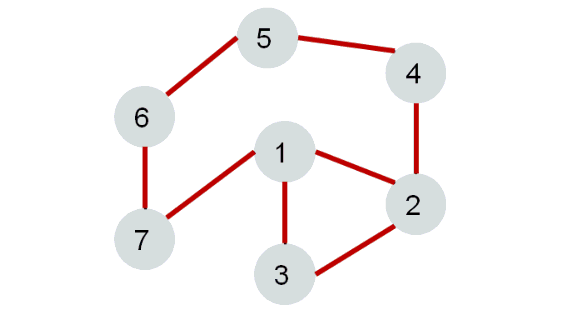
Каждая вершина может находиться в одном из 3 состояний:
- 0 — оранжевый: необнаруженная вершина.
- 1 — зеленый: обнаруженная, но не посещенная вершина.
- 2 — серый: обработанная вершина.
- Фиолетовый: рассматриваемая вершина.

Реализация поиска в ширину

Обход в ширину на матрице смежности

PythonC++

from collections import deque

# Ввод количества вершин и рёбер
vertex_count, edge_count = map(int, input("Введите количество вершин и рёбер: ").split())

# Инициализация матрицы смежности
adj_matr = [[False] * vertex_count for _ in range(vertex_count)]

# Ввод рёбер и заполнение матрицы смежности
print("Введите рёбра (по одному на строку):")
for _ in range(edge_count):
    u, v = map(int, input().split())
    u -= 1  # Индексация с 0
    v -= 1  # Индексация с 0
    adj_matr[u][v] = True  # Ориентированный граф
    adj_matr[v][u] = True  # Для неориентированного графа

# Массив для хранения расстояний
dist = [None] * vertex_count

# Стартовая вершина (в Python индекс начинается с 0, так что вершина 1 - это индекс 0)
start = 0

# Инициализация очереди и расстояния для стартовой вершины
queue = deque()
queue.append(start)
dist[start] = 0

# Обход в ширину
while queue:
    vertex = queue.popleft()
    for to in range(vertex_count):
        if adj_matr[vertex][to] and dist[to] is None:
            queue.append(to)
            dist[to] = dist[vertex] + 1

# Вывод расстояний до всех вершин
print("Расстояния от стартовой вершины:")
for i in range(vertex_count):
    print(f"До вершины {i + 1}: {dist[i]}")

#include <iostream>
#include <vector>
#include <queue>

using namespace std;

int main() {
    int vertex_count, edge_count;
    cout << "Введите количество вершин и рёбер: ";
    cin >> vertex_count >> edge_count;

    // Инициализация матрицы смежности
    vector<vector<bool>> adj_matr(vertex_count, vector<bool>(vertex_count, false));

    // Ввод рёбер и заполнение матрицы смежности
    cout << "Введите рёбра (по одному на строку, с номерами вершин):\n";
    for (int i = 0; i < edge_count; i++) {
        int u, v;
        cin >> u >> v;
        u--;  // Индексация с 0
        v--;  // Индексация с 0
        adj_matr[u][v] = true;  // Ориентированный граф
        adj_matr[v][u] = true;  // Для неориентированного графа (если нужно)
    }

    // Массив для хранения расстояний
    vector<int> dist(vertex_count, -1);  // Изначально все вершины недостижимы

    // Стартовая вершина
    int start = 0;

    // Инициализация очереди и расстояния для стартовой вершины
    queue<int> q;
    q.push(start);
    dist[start] = 0;

    // Обход в ширину
    while (!q.empty()) {
        int vertex = q.front();
        q.pop();

        for (int to = 0; to < vertex_count; to++) {
            if (adj_matr[vertex][to] && dist[to] == -1) {  // Если вершина ещё не посещена
                q.push(to);
                dist[to] = dist[vertex] + 1;
            }
        }
    }

    // Вывод расстояний до всех вершин
    cout << "Расстояния от стартовой вершины:\n";
    for (int i = 0; i < vertex_count; i++) {
        cout << "До вершины " << i + 1 << ": " << dist[i] << endl;
    }

    return 0;
}

Обход в ширину на списках смежности

PythonC++

from collections import deque

# Ввод числа вершин и рёбер
vertex_count, edge_count = map(int, input("Введите количество вершин и рёбер: ").split())

# Инициализация списка смежности
adj_list = [[] for _ in range(vertex_count)]

# Ввод рёбер
print("Введите рёбра (по одному на строку):")
for _ in range(edge_count):
    u, v = map(int, input().split())
    u -= 1  # Индексация с 0
    v -= 1  # Индексация с 0
    adj_list[u].append(v)
    adj_list[v].append(u)  # Если граф неориентированный

# Инициализация массива расстояний
dist = [None] * vertex_count

# Выбор стартовой вершины (например, вершина 0)
start = 0

# Инициализация очереди и расстояния для стартовой вершины
queue = deque([start])
dist[start] = 0

# Обход в ширину
while queue:
    vertex = queue.popleft()
    for to in adj_list[vertex]:
        if dist[to] is None:  # Если вершина ещё не посещена
            queue.append(to)
            dist[to] = dist[vertex] + 1  # Расстояние до вершины

# Вывод расстояний до всех вершин
print("Расстояния от стартовой вершины:")
print(dist)

#include <iostream>
#include <vector>
#include <queue>

using namespace std;

int main() {
    int vertex_count, edge_count;

    // Ввод числа вершин и рёбер
    cout << "Введите количество вершин и рёбер: ";
    cin >> vertex_count >> edge_count;

    // Инициализация списка смежности
    vector<vector<int>> adj_list(vertex_count);

    // Ввод рёбер
    cout << "Введите рёбра (по одному на строку):\n";
    for (int i = 0; i < edge_count; ++i) {
        int u, v;
        cin >> u >> v;
        u -= 1;  // Индексация с 0
        v -= 1;  // Индексация с 0
        adj_list[u].push_back(v);
        adj_list[v].push_back(u);  // Если граф неориентированный
    }

    // Массив для хранения расстояний
    vector<int> dist(vertex_count, -1);

    // Стартовая вершина
    int start = 0;

    // Инициализация очереди и расстояния для стартовой вершины
    queue<int> q;
    q.push(start);
    dist[start] = 0;

    // Обход в ширину
    while (!q.empty()) {
        int vertex = q.front();
        q.pop();

        for (int to : adj_list[vertex]) {
            if (dist[to] == -1) {  // Если вершина ещё не посещена
                q.push(to);
                dist[to] = dist[vertex] + 1;  // Расстояние до вершины
            }
        }
    }

    // Вывод расстояний до всех вершин
    cout << "Расстояния от стартовой вершины:\n";
    for (int i = 0; i < vertex_count; ++i) {
        cout << "До вершины " << i + 1 << ": " << dist[i] << endl;
    }

    return 0;
}

Время работы обхода в ширину при использовании списков смежности составляет О(п + m), где п — число вершин, m — число ребер, поскольку в худшем случае обход в ширину обработает каждую вершину и пройдет по всем спискам смежности.

Задание: Что такое очередь?

Примеры задач на обход графа

Далее представлены серия задач с решениями. Постарайтесь сначала прочесть формулировку и ответить на вопрос как обходить граф в данных условиях?
Ответ на этот вопрос поможем вам лучше понять различия данных методов

Задача о компьютерном кластере [1]

Постановка задачи. Представьте себе кластер серверов, состоящий из n компьютеров, соединённых сетью кабелей. Мы говорим, что два компьютера находятся на быстрой связи, если между ними можно передать данные, пройдя не более чем через к промежуточных машин. Например, при кappa = 0 только те компьютеры, которые напрямую подключены друг к другу кабелем, считаются связанными быстрой связью. Ваша задача — подсчитать, сколько машин соедено напримую с компьютера №1 через такую быструю связь.

Входные данные содержат число n (количество компьютеров), параметр V и число E (количество прямых соединений). Затем следуют E строк, каждая из которых описывает пару чисел, указывающих на два компьютера, соединённых кабелем. Необходимо вывести одно число — сколько компьютеров могут быть связаны с первым через быструю связь, соблюдая ограничения на количество промежуточных узлов.

Пример входных данных:

6 1 5 
1 2 
2 3 
1 4 
4 5 
5 6

Пример выходных данных:

4

В данном примере:
- Есть 6 компьютеров.
- Параметр кappa = 1 (разрешается не более 1 промежуточного компьютера).
- 5 прямых соединений, описанных во входных данных.

Компьютер №1 напрямую соединён с компьютерами №2 и №4.
Через один промежуточный компьютер (при к = 1) от компьютера №1 можно достичь:
- Компьютера №3 (путь: 1 → 2 → 3)
- Компьютера №5 (путь: 1 → 4 → 5)

Таким образом, с компьютера №1 можно достичь 4-х компьютеров (№2, №3, №4, №5) по быстрой связи.

Подсказки для решения задачи

• Построение графа:
  Прочитайте число компьютеров (n), параметр k (максимальное число промежуточных узлов) и число прямых соединений (t). Затем создайте список смежности, где для каждого компьютера хранится список компьютеров, с которыми он напрямую соединён.

• Обход графа:
  Используйте алгоритм обхода в ширину (BFS) начиная с компьютера №1 (индекс 0).

• При обходе фиксируйте уровень (расстояние) каждой вершины.

• Путь от компьютера №1 до другого компьютера считается допустимым, если количество ребер в пути не превышает k+1 (так как k промежуточных узлов означает k+1 ребро).

• Подсчёт результата:
  Подсчитайте количество компьютеров (за исключением стартовой вершины), для которых расстояние от компьютера №1 не больше k+1.

Задача Проверка наличия пути

Описание задачи:
Дан граф (например, в виде списка смежности). Необходимо проверить, существует ли путь между двумя заданными вершинами: начальной (s) и конечной (t). Если такой путь существует, программа должна вывести сообщение об этом, иначе – сообщение о его отсутствии.

Подсказки для решения:
- Построение графа:
Сначала считайте количество вершин и рёбер, а затем сформируйте список смежности, где для каждой вершины хранится список её соседей.

• Обход графа:
  Используйте алгоритм обхода графа (например, DFS или BFS) для проверки достижимости вершины t из вершины s. При этом важно не заходить в циклы — для этого поддерживайте массив (или множество) посещённых вершин.

• Проверка результата:
  Если вершина t была посещена в ходе обхода, значит, путь существует; иначе — его нет.

Cвязанные с темой индивидуальные проекты

Вся литература находит на яндекс диске

Алгоритм решения задачи заливки однородной области

[Алгоритм заливки](https://www.techiedelight.com/ru/flood-fill-algorithm/)

Опрный список литературы

1. Алгоритмический тренинг. Решения практических задач на Python и C++. — СПб.: БХВ-Петербург, 2023. —416 с.: ил. ISBN 978-5-9775-1168-1