Практика 8 Деревья. Идея индексирования данных.#
Деревья заслуживают отдельного и подробного рассмотрения по двум причинам:
-
Деревья являются в некотором смысле простейшим классом графов. Для них выполняются многие интересные утверждения, которые не всегда выполняются для графов в общем случае. Применительно к деревьям многие доказательства и рассуждения оказываются намного проще. Выдвигая какие-то гипотезы при решении задач теории графов, целесообразно сначала их проверять на деревьях.
-
Деревья являются самым распространённым классом графов, применяемых в программировании, причём в самых разных ситуациях. Более половины объёма этой главы посвящено рассмотрению конкретных применений деревьев в программировании.
Определение
Дерево — это связный ациклический граф
Связность означает наличие маршрута между любой парой вершин, ацикличность — отсутствие циклов.
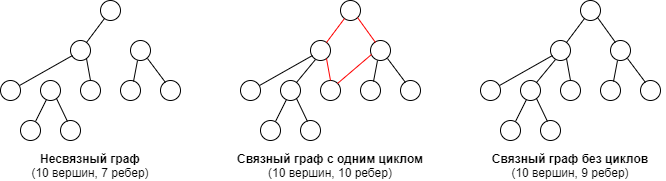
Примеры деревьев представлены ниже:
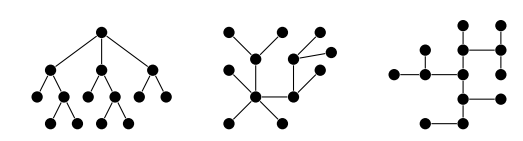
Сегодня мы будем говорить об организации хранения данных в виде дерева, что позволит обойти ограничения линейной структуры данных. Например, в последней нельзя организовать быстрыми поиск и вставку элементов одновременно. При этом в иерархической структуре данных можно эффективно выбирать и обновлять большие объемы данных.
Один из наиболее часто используемых и простых в реализации подвидов деревьев — бинарные деревья. Помимо организации поиска, бинарные деревья используют, когда разбирают математические выражения и компьютерные программы. Еще их используют, чтобы хранить данные для алгоритмов сжатия, а также они лежат в основе других структур данных, например, очереди с приоритетом, кучи и словари.
Что такое бинарные деревья#
Бинарное дерево или двоичное дерево — это дерево, в котором у каждого из его узлов не более двух дочерних узлов. При этом каждый дочерний узел тоже представляет собой бинарное дерево.
Рассмотрим примеры деревьев на следующем рисунке:
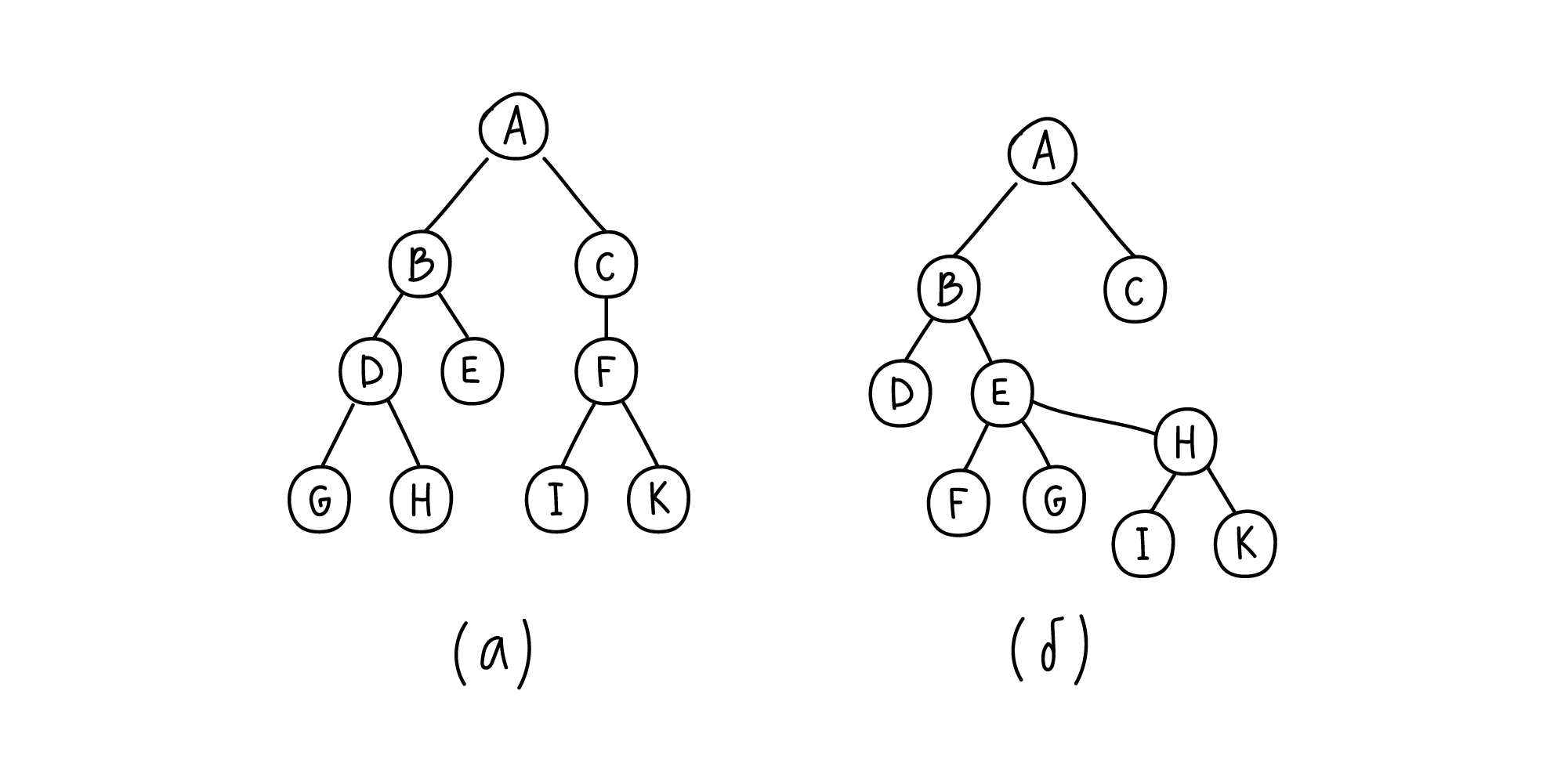
Дерево (а) — бинарное. У каждого его узла не более двух дочерних узлов, у каждого из которых тоже не более двух дочерних. Например, узлы E, G, H, I и K — листовые, значит, у них ноль дочерних узлов. У узла C только один дочерний узел, а у узлов A, B, D и F по два дочерних.
Как только правило двух дочерних нарушается, то дерево перестает относиться к классу бинарных. Так, дерево (б) не является бинарным, так как у узла E три дочерних узла.
Благодаря тому, что дочерних узлов всегда не больше двух, их называют правый и левый дочерний узел.
Напомним, что есть завершенное и полное деревья. Для бинарных деревьев они приобретают следующий вид:
-
Завершенное бинарное дерево — это бинарное дерево, в котором каждый уровень, кроме последнего, полностью заполнен, а заполнение последнего уровня производится слева направо.
-
Полное бинарное дерево — это бинарное дерево, в котором у каждого узла ноль или два дочерних узла.
На практике чаще применяются два подвида бинарных деревьев: бинарные деревья поиска и бинарные кучи. Последние разберем в следующих уроках, а в этом сосредоточимся на первых.
Question
Сколько узлов в полном бинарном дереве?
А сколько ребер?
Tip
Количество узлов: Если дерево имеет n уровней (где корень — уровень 1), то количество узлов в полном бинарном дереве можно выразить формулой:
Количество рёбер: В любом дереве количество рёбер всегда на 1 меньше, чем количество узлов. То есть:
E= N−1
Реализация бинарных деревьев#
Определим метод __init__(). Как всегда, он принимает self. Также мы передаем в него значение, которое будет храниться в узле. Установим значение узла, а затем определим левый и правый указатель (для начала поставим им значение None).
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
И… все! Если речь идет о двоичном дереве, единственное, что его отличает от связного списка, это то, что вместо next у нас тут есть left и right.
Давайте построим дерево, которое изображено на схеме в начале статьи. Верхний узел имеет значение 1. Далее мы устанавливаем левые и правые узлы, пока не получим желаемое дерево.
tree = TreeNode(1)
tree.left = TreeNode(2)
tree.right = TreeNode(3)
tree.left.left = TreeNode(4)
tree.left.right = TreeNode(5)
Для представления одной вершины (узла) двоичного дерева поиска создадим класс TreeNode. У элементов этого класса будут следующие поля:
val - данные (число), которые хранятся в этой вершине.
left - указатель на левого потомка данной вершины.
right - указатель на правого потомка данной вершины.
class TreeNode {
public:
int val; // Значение узла
TreeNode* left; // Указатель на левый дочерний узел
TreeNode* right; // Указатель на правый дочерний узел
// Конструктор класса
// Принимает значение узла и указатели на левый и правый узлы (по умолчанию nullptr, что аналог None)
TreeNode(int val = 0, TreeNode* left = nullptr, TreeNode* right = nullptr)
: val(val), left(left), right(right) {} // Инициализация членов класса
};
И… все! Если речь идет о двоичном дереве, единственное, что его отличает от связного списка, это то, что вместо next у нас тут есть left и right.
Давайте построим дерево, которое изображено на схеме в начале статьи. Верхний узел имеет значение 1. Далее мы устанавливаем левые и правые узлы, пока не получим желаемое дерево.
int main() {
// Создаем корневой узел дерева со значением 1.
TreeNode* tree = new TreeNode(1);
// Создаем левый дочерний узел от корневого узла со значением 2.
tree->left = new TreeNode(2);
// Создаем правый дочерний узел от корневого узла со значением 3.
tree->right = new TreeNode(3);
// Создаем левый дочерний узел от узла со значением 2 со значением 4.
tree->left->left = new TreeNode(4);
// Создаем правый дочерний узел от узла со значением 2 со значением 5.
tree->left->right = new TreeNode(5);
// Выводим значения узлов для проверки построенного дерева.
std::cout << "Root: " << tree->val << std::endl;
std::cout << "Левый потомок от корня " << tree->left->val << std::endl;
std::cout << "Правый потомок от корня" << tree->right->val << std::endl;
std::cout << "Левый потомок от 2 узла: " << tree->left->left->val << std::endl;
std::cout << "Правый потомок от 2 узла: " << tree->left->right->val << std::endl;
// Освобождаем память, чтобы избежать утечек памяти.
delete tree->left->left;
delete tree->left->right;
delete tree->left;
delete tree->right;
delete tree;
return 0;
}
Задание: Напишите функицю визуализации дерева в консоли, которая выведет следующее для нашего дерева:
Root: 1
L--- 2
L--- 4
R--- 5
R--- 3
Функция и её интерфейс
- Название функции: print_tree
- Аргументы:
- node – корневой узел дерева.
- level (необязательный) – текущий уровень узла в дереве (по умолчанию 0).
- prefix (необязательный) – строка, которая выводится перед значением узла (по умолчанию "Root: ").
Функция должна рекурсивно проходить по дереву, печатать значение узла с отступом, зависящим от уровня, и вызывать себя для левого и правого потомков.
- Рекурсивная реализация: Функция должна использовать рекурсию для обхода дерева.
- Уровни и отступы: Количество пробелов перед узлом должно равняться
level * 4. - Префиксы:
- Корневой узел выводится с префиксом
"Root: ". - Левые узлы – с префиксом
"L--- ". - Правые узлы – с префиксом
"R--- ". - Обработка отсутствующих узлов: Если узел отсутствует (равен
None), то выводится строка с отступом и текстом"L--- None"или"R--- None", чтобы явно показать, что дочернего узла нет. - Проверка наличия дочерних узлов: Вывод дочерних узлов осуществляется только если хотя бы один из потомков существует. Если потомков нет, можно не выводить их строки.
Обход деревьев#
Итак, вы построили дерево и теперь вам, вероятно, любопытно, как же его увидеть. Нет никакой команды, которая позволила бы вывести на экран дерево целиком, тем не менее мы можем обойти его, посетив каждый узел. Но в каком порядке выводить узлы?
Самые простые в реализации обходы дерева — прямой (Pre-Order), обратный (Post-Order) и центрированный (In-Order). Вы также можете услышать такие термины, как поиск в ширину и поиск в глубину, но их реализация сложнее, ее мы рассмотрим как-нибудь потом.
Итак, что из себя представляют три варианта обхода, указанные выше? Давайте еще раз посмотрим на наше дерево.
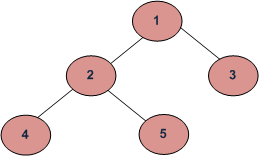
При прямом обходе мы посещаем родительские узлы до посещения узлов-потомков. В случае с нашим деревом мы будем обходить узлы в таком порядке: 1, 2, 4, 5, 3.
Обратный обход двоичного дерева — это когда вы сначала посещаете узлы-потомки, а затем — их родительские узлы. В нашем случае порядок посещения узлов при обратном обходе будет таким: 4, 5, 2, 3, 1.
При центрированном обходе мы посещаем все узлы слева направо. Центрированный обход нашего дерева — это посещение узлов 4, 2, 5, 1, 3.
Note
Прямой обход (КЛП): корень → левое поддерево → правое поддерево
Центрированный обход (ЛКП): левое поддерево → корень → правое поддерево
Обратный обход (ЛПК): левое поддерево → правое поддерево → корень
Давайте напишем методы обхода для нашего двоичного дерева.
Прямой обход (Pre-Order)#
Начнем с определения метода pre_order(). Наш метод принимает один аргумент — корневой узел (расположенный выше всех).
def pre_order(node):
pass
Дальше нам нужно проверить, существует ли этот узел. Вы можете возразить, что лучше бы проверить существование потомков этого узла перед их посещением. Но для этого нам пришлось бы написать два if-предложения, а так мы обойдемся одни
def pre_order(node):
if node:
pass
Написать обход просто. Прямой обход — это посещение родительского узла, а затем каждого из его потомков. Мы «посетим» родительский узел, выведя его на экран, а затем «обойдем» детей, вызывая этот метод рекурсивно для каждого узла-потомка.
# Выводит родителя до всех его потомков
def pre_order(node):
if node:
print(node.value)
pre_order(node.left)
pre_order(node.right)
Просто, правда? Можем протестировать этот код, совершив обход построенного ранее дерева.
Начнем с определения метода pre_order(). Наш метод принимает один аргумент — корневой узел (расположенный выше всех).
oid pre_order(TreeNode* node) {
}
Дальше нам нужно проверить, существует ли этот узел. Вы можете возразить, что лучше бы проверить существование потомков этого узла перед их посещением. Но для этого нам пришлось бы написать два if-предложения, а так мы обойдемся одним.
oid pre_order(TreeNode* node) {
if (node) {
// действия
}
}
Написать обход просто. Прямой обход — это посещение родительского узла, а затем каждого из его потомков. Мы «посетим» родительский узел, выведя его на экран, а затем «обойдем» детей, вызывая этот метод рекурсивно для каждого узла-потомка.
// Выводит родителя до всех его потомков
void pre_order(TreeNode* node) {
if (node) {
std::cout << node->val << std::endl; // Выводим значение родительского узла
pre_order(node->left); // Рекурсивно обходим левое поддерево
pre_order(node->right); // Рекурсивно обходим правое поддерево
}
}
Просто, правда? Можем протестировать этот код, совершив обход построенного ранее дерева.
Обратный (Post-Order)#
Переходим к обратному обходу. Возможно, вы думаете, что для этого нужно написать еще один метод, но на самом деле нам нужно изменить всего одну строчку в предыдущем.
Вместо «посещения» родительского узла и последующего «обхода» детей, мы сначала «обойдем» детей, а затем «посетим» родительский узел. То есть, мы просто передвинем print на последнюю строку! Не забудьте поменять имя метода на post_order() во всех вызовах.
# Выводит потомков, а затем родителя
def post_order(node):
if node:
post_order(node.left)
post_order(node.right)
print(node.value)
Для обратного обхода в C++ нужно немного изменить код, переместив вывод значения узла в конце обхода, как вы описали. Вот пример аналогичного метода post_order() на C++:
void post_order(TreeNode* node) {
if (node) {
post_order(node->left); // Рекурсивно обходим левое поддерево
post_order(node->right); // Рекурсивно обходим правое поддерево
std::cout << node->val << std::endl; // Выводим значение родительского узла
}
}
Центрированный обход(In-Order)#
Наконец, напишем метод центрированного обхода. Как нам обойти левый узел, затем родительский, а затем правый? Опять же, нужно переместить предложение print!
# выводит левого потомка, затем родителя, затем правого потомка
def in_order(node):
if node:
in_order(node.left)
print(node.value)
in_order(node.right)
Для центрированного обхода в C++ аналогично нужно переместить вывод значения узла между рекурсивными вызовами для левого и правого поддеревьев. Вот пример метода in_order() на C++:
void in_order(TreeNode* node) {
if (node) {
in_order(node->left); // Рекурсивно обходим левое поддерево
std::cout << node->val << std::endl; // Выводим значение родительского узла
in_order(node->right); // Рекурсивно обходим правое поддерево
}
}
Поиск в двоичном дереве#
Как можно понять по названию, основное преимущество бинарных деревьев поиска в том, что в них можно легко производить поиск элементов, однако перед этим нужно закрепить правила вставки.
Вставка элементов в бинарное дерево поиска (BST) основана на правилах, которые позволяют упорядочивать элементы в дереве так, чтобы для каждого узла значения в левом поддереве были меньше, а в правом — больше. Вставка происходит рекурсивно, проходя по дереву, начиная с корня, и вставляя элементы в соответствующее поддерево в зависимости от их значения.
# выводит левого потомка, затем родителя, затем правого потомка
def insert(self, value):
# Если значение меньше текущего, вставляем в левое поддерево
if value < self.value:
if self.left:
self.left.insert(value) # Рекурсивно ищем место в левом поддереве
else:
self.left = TreeNode(value) # Вставляем новый узел
# Если значение больше текущего, вставляем в правое поддерево
elif value > self.value:
if self.right:
self.right.insert(value) # Рекурсивно ищем место в правом поддереве
else:
self.right = TreeNode(value) # Вставляем новый узел
Попробуйте построить разные деревья и вывести их значения
root = TreeNode(10)
root.insert(5)
root.insert(15)
root.insert(3)
root.insert(7)
Вставка элементов в бинарное дерево поиска (BST) основана на правилах, которые позволяют упорядочивать элементы в дереве так, чтобы для каждого узла значения в левом поддереве были меньше, а в правом — больше. Вставка происходит рекурсивно, проходя по дереву, начиная с корня, и вставляя элементы в соответствующее поддерево в зависимости от их значения.
void insert(int value) {
// Если значение меньше текущего, вставляем в левое поддерево
if (value < val) {
if (left) {
left->insert(value); // Рекурсивно ищем место в левом поддереве
} else {
left = new TreeNode(value); // Вставляем новый узел
}
}
// Если значение больше текущего, вставляем в правое поддерево
else if (value > val) {
if (right) {
right->insert(value); // Рекурсивно ищем место в правом поддереве
} else {
right = new TreeNode(value); // Вставляем новый узел
}
}
}
Теперь реализуем функцию поиска элемента для дерева
def search(self, value):
# Если значение совпадает с текущим узлом, возвращаем текущий узел
if self.value == value:
return self
# Если значение меньше текущего, ищем в левом поддереве
elif value < self.value and self.left:
return self.left.search(value)
# Если значение больше текущего, ищем в правом поддереве
elif value > self.value and self.right:
return self.right.search(value)
# Если узел не найден, возвращаем None
else:
return None
Вывод надйенного значения:
result = root.search(7)
if result:
print(f"Значение {result.value} найдено в дереве.")
else:
print("Значение не найдено.")
Модифицируйте функцию таким образом, чтобы выводилось количество сравнений, выполняемых в ходе обхода дерева.
Составьте таблицу наблюдений.
// Метод поиска элемента в дереве
TreeNode* search(int value) {
// Если значение совпадает с текущим узлом, возвращаем текущий узел
if (val == value) {
return this;
}
// Если значение меньше текущего, ищем в левом поддереве
else if (value < val && left) {
return left->search(value);
}
// Если значение больше текущего, ищем в правом поддереве
else if (value > val && right) {
return right->search(value);
}
// Если узел не найден, возвращаем nullptr
return nullptr;
}
Вывод надйенного значения:
int search_value = 7;
TreeNode* result = root->search(search_value);
if (result) {
std::cout << "Значение " << result->val << " найдено в дереве." << std::endl;
} else {
std::cout << "Значение не найдено." << std::endl;
}
Модифицируйте функцию таким образом, чтобы выводилось количество сравнений, выполняемых в ходе обхода дерева.
Составьте таблицу наблюдений.
Note
Эта функция — как и многие другие основные, например, вставка или удаление элементов — работает в худшем случае за высоту дерева. Высота бинарного дерева в худшем случае может быть
O(n) («бамбук»), поэтому в эффективных реализациях поддерживаются некоторые инварианты, гарантирующие среднюю глубину вершины O(log n) и соответствующую стоимость основных операций. Такие деревья называются сбалансированными.
Деревья в практике программирования. Kd-деревья#
Note
KD-дерево (K-мерное дерево) — структура данных, которая разделяет многомерное пространство на области, связанные с определёнными точками данных
Для иллюстрации работы точечного kD-дерева будем использовать семь точек: A, B, C, D, E, F и G. Эти точки отмечены на рисунке и имеют следующие координаты:
| Точка | X | Y |
|---|---|---|
| A | 2 | 2 |
| B | 0 | 5 |
| C | 8 | 0 |
| D | 9 | 8 |
| E | 7 | 14 |
| F | 13 | 12 |
| G | 14 | 13 |
Точки добавляются в дерево по порядку: A, B, C, ..., G. Этот порядок важен для правильного построения дерева.
- Первая точка, A, используется для разбиения пространства по координате X. Это создает корень дерева с двумя ветвями.
- Вторая точка, B, используется для разбиения пространства по координате Y. Если X точки B меньше, чем X точки A, точка B вставляется в левую ветвь.
- Точка C вставляется, начиная с корня. Если X точки C больше, чем X точки A, точка C идет в правую ветвь.
Процесс повторяется, чередуя использование координат X и Y на каждом уровне дерева. Важно, что в корне всегда используется координата X.
Левая часть рисунка иллюстрирует процесс добавления точек в дерево.
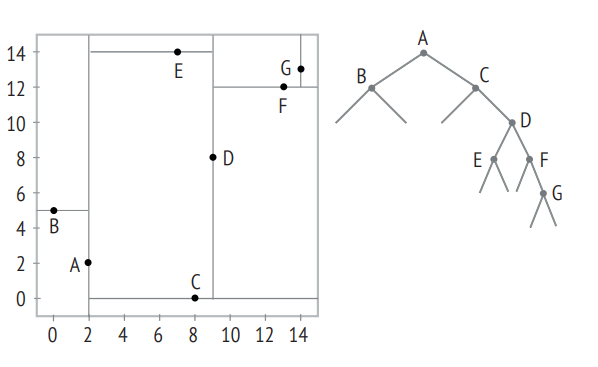
Для поиска информации о точке F на карте, мы начинаем с корня kD-дерева. Поскольку координата X точки F больше, чем у корня, идем по правой ветви, где находится точка C. Это не нужная нам точка, поэтому продолжаем поиск и сравниваем координаты Y между искомой точкой и точкой C. Поскольку Y точки F больше, чем у точки C, идем по правой ветви, которая ведет нас к точке D.
Далее сравниваем координаты X между точкой F и точкой D. Поскольку X точки F больше, продолжаем поиск по правой ветви, и находим точку F.
Если глубина корня равна 0, то в процессе поиска мы сравнивали координаты X на четных уровнях и координату Y на нечетных. Таким образом, на каждом шаге исключались половина ветвей, что делает поиск эффективным.
Задание: Давайте попытаемся реализовать. Для чего вновь перепишем код.
- Добавьте функцию
range_searchПоиск основан на обычном спуске по дереву, когда каждый узел проверяется на диапазон. Если медианы узла меньше или больше заданного диапазона в данном пространстве, то обход идет дальше по одной из ветвей дерева. Если же медиана узла входит полностью в заданный диапазон, то нужно посетить оба поддерева.
Покажем псевдокод функции range_search
Функция range_search(узел, нижняя_граница, верхняя_граница, глубина, результат)
Если узел == NULL
Вернуть
ось = глубина % размер_точки
// Проверяем, находится ли текущий узел внутри заданного диапазона
если все координаты узла находятся в пределах [нижняя_граница, верхняя_граница]
добавить узел в результат
// Рекурсивный обход поддеревьев
если узел.левый существует и нижняя_граница[ось] ≤ узел.точка[ось]
вызвать range_search(узел.левый, нижняя_граница, верхняя_граница, глубина + 1, результат)
если узел.правый существует и верхняя_граница[ось] ≥ узел.точка[ось]
вызвать range_search(узел.правый, нижняя_граница, верхняя_граница, глубина + 1, результат)
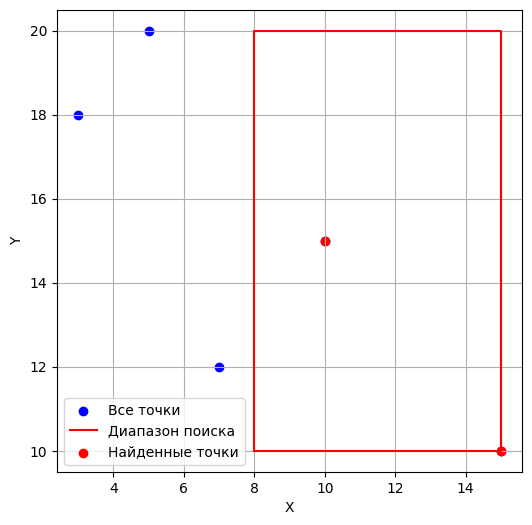
Пример для диапазона lower_bound = (8, 10), upper_bound = (15, 20) для точек points = [(10, 15), (5, 20), (15, 10), (3, 18), (7, 12)]
Повторение#
Произвеите О-оценку следующего алгоритма:
1 Линейный поиск элемента массива
def linear_search(arr, target):
for i in range(len(arr)):
if arr[i] == target:
return i
return -1
arr = [1, 3, 5, 7, 9]
target = 7
result = linear_search(arr, target)
print(f"Элемент найден. Его номер {result}" if result != -1 else "Не найдено")
#include <iostream>
using namespace std;
int linearSearch(int arr[], int size, int target) {
for (int i = 0; i < size; i++) {
if (arr[i] == target) {
return i;
}
}
return -1;
}
int main() {
int arr[] = {1, 3, 5, 7, 9};
int target = 7;
int size = sizeof(arr) / sizeof(arr[0]);
int result = linearSearch(arr, size, target);
cout << (result != -1 ? "Элемент найден. Его номер " : "Не найдено") << result << endl;
return 0;
}
2 Бинарное возведение в степень
def power(a, n):
if n == 0:
return 1
half = power(a, n // 2)
return half * half if n % 2 == 0 else half * half * a
print(power(2, 10)) # 1024
#include <iostream>
long long power(long long a, long long n) {
if (n == 0) return 1;
long long half = power(a, n / 2);
if (n % 2 == 0) return half * half;
return half * half * a;
}
int main() {
std::cout << power(2, 10); // 1024
return 0;
}
3 Поиск в возвратом для лабиринта
Tip
Для оценки надо ответить на несколько сопутвующих:
1. Какая оценка верхней границы (что есть худший случай)
2. Поиск с возратом является частным случаем полного перебора
3. Какой лучший случай?
4. Заивисит ли лучший случай от структуры лабиринта?
N = 5
maze = [
[0, 1, 0, 0, 0],
[0, 1, 0, 1, 0],
[0, 0, 0, 1, 0],
[0, 1, 1, 1, 0],
[0, 0, 0, 0, 0]
]
visited = [[False] * N for _ in range(N)]
directions = [(1, 0), (0, 1), (-1, 0), (0, -1)] # Вправо, вниз, вверх, влево
def solve(x, y):
if x == N - 1 and y == N - 1: # Достигли выхода
return True
visited[x][y] = True
for dx, dy in directions:
nx, ny = x + dx, y + dy
if 0 <= nx < N and 0 <= ny < N and maze[nx][ny] == 0 and not visited[nx][ny]:
if solve(nx, ny):
return True
visited[x][y] = False # Возврат назад
return False
if solve(0, 0):
print("Путь найден!")
else:
print("Пути нет.")
#include <iostream>
using namespace std;
const int N = 5;
int maze[N][N] = { // 0 - проход, 1 - стена
{0, 1, 0, 0, 0},
{0, 1, 0, 1, 0},
{0, 0, 0, 1, 0},
{0, 1, 1, 1, 0},
{0, 0, 0, 0, 0}
};
bool visited[N][N] = {false};
int dx[] = {1, 0, 0, -1}; // Вправо, вниз, вверх, влево
int dy[] = {0, 1, -1, 0};
bool solve(int x, int y) {
if (x == N - 1 && y == N - 1) { // Достигли выхода
return true;
}
visited[x][y] = true;
for (int i = 0; i < 4; i++) {
int nx = x + dx[i], ny = y + dy[i];
if (nx >= 0 && ny >= 0 && nx < N && ny < N && maze[nx][ny] == 0 && !visited[nx][ny]) {
if (solve(nx, ny)) return true;
}
}
visited[x][y] = false; // Возврат
return false;
}
int main() {
if (solve(0, 0)) cout << "Путь найден!\n";
else cout << "Пути нет.\n";
return 0;
}
Cвязанные с темой индивидуальные проекты#
Вся литература находит на яндекс диске
Реализации деревьев для трассировки лучей
Стр 86-109 Сяо H. Алгоритмы ГИС / пер. с англ. А. А. Слинкина. – М.: ДМК Пресс, 2021. – 328 с.: ил. ISBN 978-5-97060-908-8
Для желающих продолжить*#

Братец кролик продолжал делать странные вещи с компьютером. Однажды он решил назвать папку на компьютере невинным словом Con. Что произошло дальше никому не известно, но всем было очень страшно. Попытайтесь на Windows назвать так папку. Затем попытайтесь объясить произошедшее (Секретное слово вызывающее странное поведение системы спрятано в тексте)
Ответы о причинах необычного поведения Windows и само слово присылайте письмом.