Практика 7 Алгоритмы поиска с возвратом и обхода дерева#
Есть такие задачи, где нужно перебрать все варианты решения, чтобы убедиться, что найден нужный ответ и ничего не пропущено. Например, когда решалась кодом задача сортировки массива, то в первой версии сортировкой пузырьком перебирались все возможные комбинации.
Алгоритм поиска с возвратом тоже относится к полным переборам, но у него есть особенность, которая делает этот перебор проще:
если алгоритм понимает, что идёт по неверному пути, то все остальные варианты в этом пути тоже помечаются как неправильные и не рассматриваются.
Получается, что перебираются только те варианты, в которых потенциально есть решение, — а это сильно сокращает время перебора даже без специальной оптимизации.
Как это работает в теории#
Ключевой элемент поиска с возвратом — рекурсия, то есть функция, которая вызывает сама себя. Работа рекурсии часто требует много оперативной памяти, но из-за особенностей алгоритма памяти нужно гораздо меньше, чем при полном переборе «в лоб».
Алгоритм поиска с возвратом состоит из трёх частей:
- Рекурсия, которая получает очередную комбинацию для проверки и уходит вглубь себя, раскладывая всё по полочкам.
- Генератор вариантов, который создаёт новую цепочку данных и отправляет их в рекурсию.
- Модуль проверки, который оценивает, идёт ли рекурсия по верному пути, и если да — то нашла ли она решение в итоге или нет.
функция backtrack(текущее_решение):
если решение полное:
обработать результат
вернуть
для каждого возможного выбора:
если выбор допустим:
сделать выбор
рекурсивно продолжить поиск
отменить выбор (откат)
def backtrack(path, choices):
if not choices:
print(path) # Базовый случай: вывод готового решения
return
for i in range(len(choices)):
backtrack(path + [choices[i]], choices[:i] + choices[i+1:])
backtrack([], [1, 2, 3])
#include <iostream>
#include <vector>
void backtrack(std::vector<int> path, std::vector<int> choices) {
if (choices.empty()) {
for (int num : path) {
std::cout << num << " ";
}
std::cout << std::endl;
return;
}
for (size_t i = 0; i < choices.size(); ++i) {
std::vector<int> newPath = path;
newPath.push_back(choices[i]);
std::vector<int> newChoices = choices;
newChoices.erase(newChoices.begin() + i);
backtrack(newPath, newChoices);
}
}
int main() {
std::vector<int> nums = {1, 2, 3};
backtrack({}, nums);
return 0;
}
Разбор задачи Судоку#
Проиллюстрируем идею перебора с возвратом на примере поиска решения головоломки «Судоку». Игровое поле представляет собой квадрат 9×9, разделённый на меньшие квадраты 3×3. В начале игры в некоторых клетках уже записаны числа от 1 до 9.
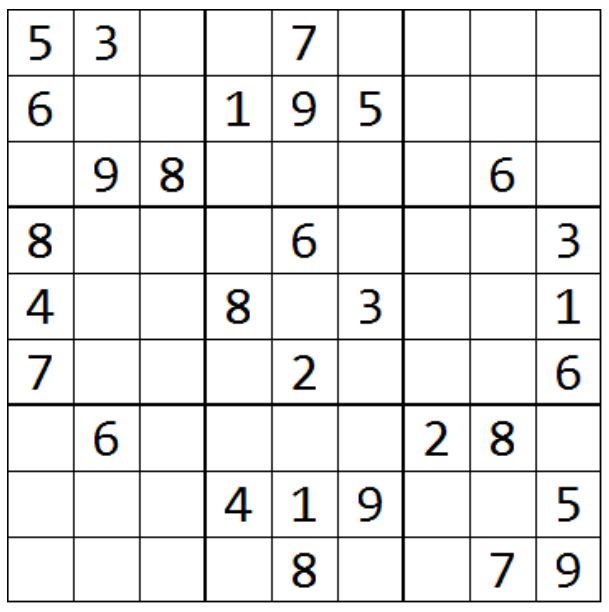
В «Судоку» есть одно правило: необходимо заполнить свободные клетки цифрами от 1 до 9 так, чтобы в каждой строке, столбце и малом квадрате 3×3 каждая цифра встречалась только один раз.
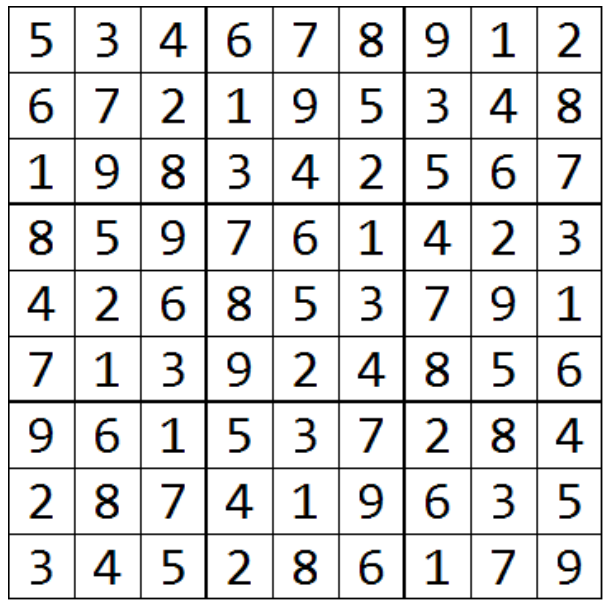
Основная идея перебора с возвратом#
На каждом шаге выбирается число для очередной клетки. Если ни одно из чисел не подходит, алгоритм возвращается назад на ближайший шаг, где ещё есть альтернативные варианты. Таким образом, перебираются только возможные решения, исключая заведомо неверные.
Формализация задачи#
Обозначим множество возможных значений для клетки как:
Решением будем считать вектор B , в котором каждый элемент соответствует числу, записанному в одной клетке. Количество элементов вектора B равно числу пустых клеток.
На i-м шаге определяем множество возможных значений S_i для клетки следующим образом:
- Включаем значение m \in M в S_i , если оно не содержится в текущей строке, столбце или малом квадрате 3×3.
- Если S_i содержит несколько элементов, упорядочиваем их в порядке множества M .
Пример работы алгоритма#
Шаг 1: Начинаем с пустого вектора:
B = ()
Шаг 2 [клетка (1,1)]:
Определяем S_1 = \{3,4,5,6\} .
Выбираем 3 → B = (3) , переходим к (1,2).
Шаг 3 [клетка (1,2)]:
Во втором столбце известны 8 из 9 клеток, оставшаяся должна иметь значение 3, но в первой строке уже есть тройка (поставленная на шаге 2), поэтому S_2 = \{\} .
Откат назад.
Шаг 4 [клетка (1,1)]:
Выбираем следующий вариант → 4 → B = (4) .
Шаг 5 [клетка (1,2)]:
S_2 = \{3\} , выбираем 3 → B = (4,3) .
Шаг 6 [клетка (1,3)]:
S_3 = \{5,6\} , выбираем 5 → B = (4,3,5) .
Шаг 7 [клетка (1,4)]:
S_4 = \{6\} , выбираем 6 → B = (4,3,5,6) .
Шаг 8 [клетка (1,6)]:
S_5 = \{8\} , выбираем 8 → B = (4,3,5,6,8) .
Текущая версия решения представлена на рисунке:
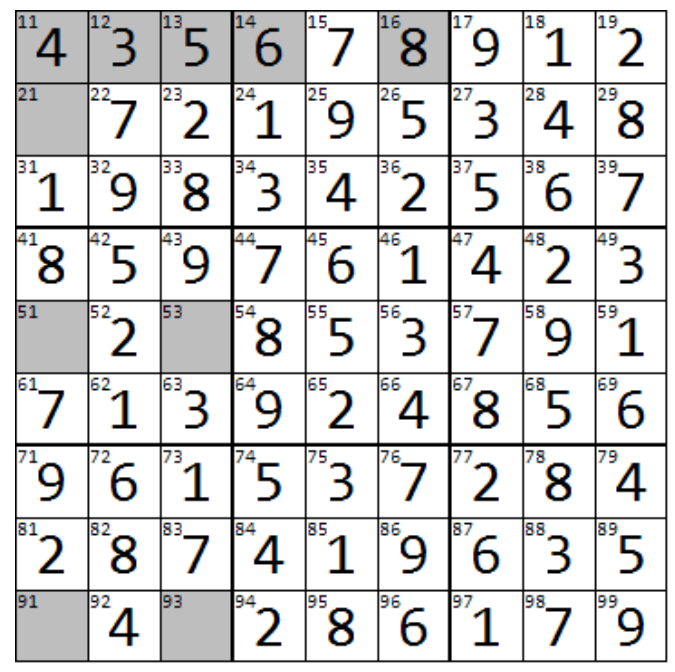
Шаг 9 [клетка (2,1)]:
S_6 = \{6\} , выбираем 6 → B = (4,3,5,6,8,6) , переходим в клетку (5,1).
Шаг 10 [клетка (5,1)]:
S_7 = \{\} — пустое множество. Возвращаемся назад в (2,1).
Так как все варианты S_6 проверены, возвращаемся в клетку (1,6) и далее до клетки, где есть ещё нерассмотренные варианты → (1,3).
Шаг 11 [клетка (1,3)]:
Выбираем следующее значение из S_3 = \{5,6\} , выбираем 6 → B = (4,3,6) .
Шаг 12 [клетка (1,4)]:
S_4 = \{\} — пустое множество. Возвращаемся назад в (1,3).
Продолжаем процесс до тех пор, пока не найдём решение или не переберём все варианты. Проиллюстрировать процесс можно в виде гиф анимации:
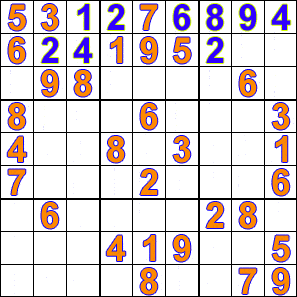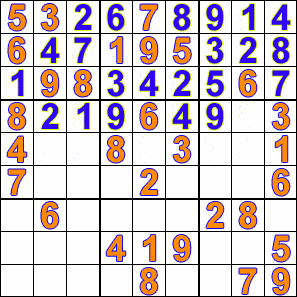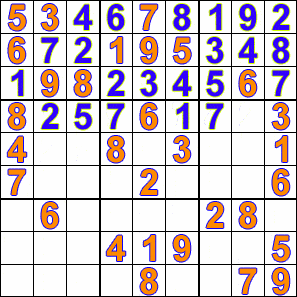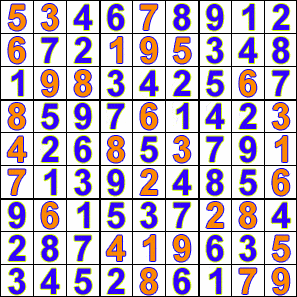
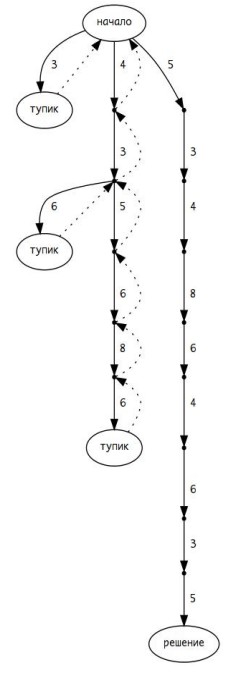
Дерево поиска с возвратом#
Решение можно представить в виде дерева, где:
- Корень — пустое частичное решение.
- Рёбра соответствуют выбору значений.
- Листья — конечные варианты.
"Сложность алгоритма"
Реализация перебора с возвратом обычно приводит к **экспоненциальным алгоритмам**, так как количество возможных решений **экспоненциально** растёт.
Заметки
Поиск с возвратом применяется в задачах комбинаторной оптимизации, например:
- для синтаксического анализа естественной речи, когда компьютеру нужно разложить текст на лексические составляющие, подобрать ответ, а потом поставить слова в ответе в правильном и естественном порядке;
- для поиска решений в задачах «про наполнение рюкзака», когда нужно найти, например, оптимальное соотношение веса, объёма и цены;
- в языках логического программирования — Prolog или Planner, которые используют этот алгоритм для создания ответов на запросы пользователя;
Задача поиска выхода из лабиринта#
Хотя лабиринты бывают разных форм и размеров, односвязные лабиринты, также называемые идеальными, не содержат замкнутых маршрутов. В этом лабиринте между любыми двумя точками (например, между входом и выходом) есть только один путь. Такие лабиринты могут быть представлены ориентированным ациклическим графом (DAG).

На рисунке показан лабиринт, который проходит наша программа, а на следующем рисунке он представлен в виде DAG. Заглавной буквой S на рисунке обозначен вход в лабиринт, а заглавной буквой E — выход из него. Несколько развилок в лабиринте, отмеченных строчными буквами, соответствуют узлам графа.
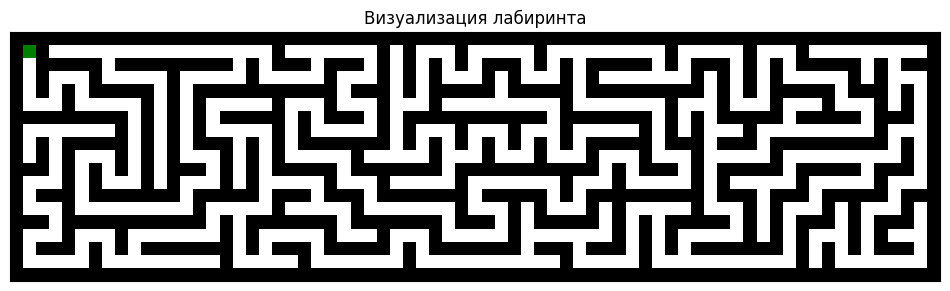
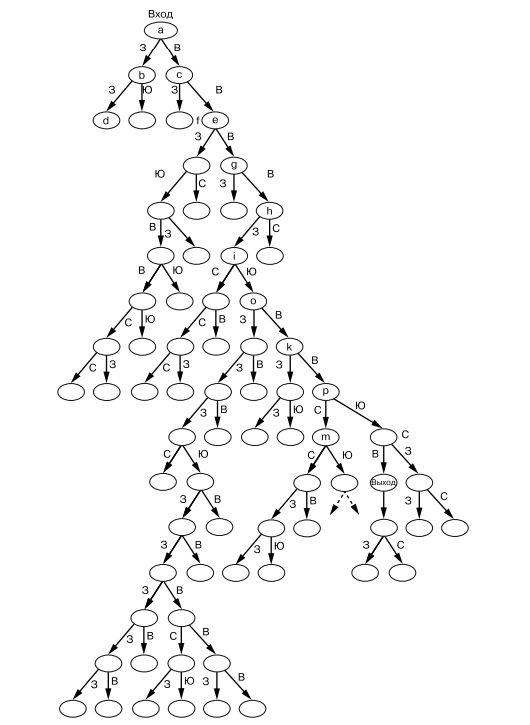
Структура данных лабиринта#
Лабиринт может быть представлен в виде многострочной строки, где каждый символ — это либо стена (#), либо свободное пространство (), либо вход (S), либо выход (E). Структура данных, содержащая лабиринт, преобразуется в список списков, что позволяет обращаться к элементам с помощью индексов.
# Создание структуры данных лабиринта:
MAZE = """
#######################################################################
#S# # # # # # # # # #
# ##### ######### # ### ### # # # # ### # # ##### # ### # # ##### # ###
# # # # # # # # # # # # # # # # # # # #
# # # ##### # ########### ### # ##### ##### ######### # # ##### ### # #
# # # # # # # # # # # # # # # # #
######### # # # ##### # ### # ########### ####### # # ##### ##### ### #
# # # # # # # # # # # # # # # # # #
# # ##### # # ### # # ####### # # # # # # # ##### ### ### ######### # #
# # # # # # # # # # # # # # # # # # #
### # # # # ### # # ##### ####### ########### # ### # ##### ##### ### #
# # # # # # # # # # # # # # # # #
# ### ####### ##### ### ### ####### ##### # ######### ### ### ##### ###
# # # # # # # # # # # # # # # # #
### ########### # ####### ####### ### # ##### # # ##### # # ### # ### #
# # # # # # # # # # # # # # # # # #
# ### # # ####### # ### ##### # ####### ### ### # # ####### # # # ### #
# # # # # # # # # E#
#######################################################################
""".split('\n')
# Константы, используемые в этой программе:
EMPTY = ' '
START = 'S'
EXIT = 'E'
PATH = '.'
# Получаем высоту и ширину лабиринта:
HEIGHT = len(MAZE)
WIDTH = 0
#include <iostream>
#include <vector>
#include <string>
using namespace std;
// Создание структуры данных лабиринта
const string MAZE[] = {
"#######################################################################",
"#S# # # # # # # # # #",
"# ##### ######### # ### ### # # # # ### # # ##### # ### # # ##### # ###",
"# # # # # # # # # # # # # # # # # # # #",
"# # # ##### # ########### ### # ##### ##### ######### # # ##### ### # #",
"# # # # # # # # # # # # # # # # #",
"######### # # # ##### # ### # ########### ####### # # ##### ##### ### #",
"# # # # # # # # # # # # # # # # # #",
"# # ##### # # ### # # ####### # # # # # # # ##### ### ### ######### # #",
"# # # # # # # # # # # # # # # # # # #",
"### # # # # ### # # ##### ####### ########### # ### # ##### ##### ### #",
"# # # # # # # # # # # # # # # # #",
"# ### ####### ##### ### ### ####### ##### # ######### ### ### ##### ###",
"# # # # # # # # # # # # # # # # #",
"### ########### # ####### ####### ### # ##### # # ##### # # ### # ### #",
"# # # # # # # # # # # # # # # # # #",
"# ### # # ####### # ### ##### # ####### ### ### # # ####### # # # ### #",
"# # # # # # # # # E#",
"#######################################################################"
};
const char EMPTY = ' ';
const char START = 'S';
const char EXIT = 'E';
const char PATH = '.';
// Получаем высоту и ширину лабиринта:
const int HEIGHT = sizeof(MAZE) / sizeof(MAZE[0]);
int WIDTH = 0;
Алгоритм обхода лабиринта#
Для нахождения пути через лабиринт используется рекурсивный алгоритм. Алгоритм работает как обход дерева, где узлы — это развилки, а листья — тупики. Алгоритм перебирает возможные пути, двигаясь по соседним клеткам, пока не найдет выход.
Базовый случай#
Базовый случай наступает, когда алгоритм достигает тупика (листа) или выходного узла. В обоих случаях алгоритм возвращается назад.
Аргументы рекурсивной функции#
- Координаты x и y — текущие координаты.
- Структура лабиринта — представление лабиринта в виде списка.
- Список visited — список посещенных точек для предотвращения зацикливания.
Шаги алгоритма:#
- Проверить, если текущая позиция — это выход (E), вернуть
True. - Пометить текущую позицию как посещенную.
- Проверить возможные соседние позиции (север, юг, восток, запад).
- Если соседняя позиция доступна (не стена и не посещена ранее), рекурсивно вызвать функцию для этой позиции.
- Если все соседние позиции не приводят к выходу, вернуть
False.
Приведем интерактивную визуализацию алгоритма и посмотрим на его поведение.
Ваша практика функция solveMaze#
Задание Дополните функцию solveMaze
# Создание структуры данных лабиринта:
MAZE = """
#######################################################################
#S# # # # # # # # # #
# ##### ######### # ### ### # # # # ### # # ##### # ### # # ##### # ###
# # # # # # # # # # # # # # # # # # # #
# # # ##### # ########### ### # ##### ##### ######### # # ##### ### # #
# # # # # # # # # # # # # # # # #
######### # # # ##### # ### # ########### ####### # # ##### ##### ### #
# # # # # # # # # # # # # # # # # #
# # ##### # # ### # # ####### # # # # # # # ##### ### ### ######### # #
# # # # # # # # # # # # # # # # # # #
### # # # # ### # # ##### ####### ########### # ### # ##### ##### ### #
# # # # # # # # # # # # # # # # #
# ### ####### ##### ### ### ####### ##### # ######### ### ### ##### ###
# # # # # # # # # # # # # # # # #
### ########### # ####### ####### ### # ##### # # ##### # # ### # ### #
# # # # # # # # # # # # # # # # # #
# ### # # ####### # ### ##### # ####### ### ### # # ####### # # # ### #
# # # # # # # # # E#
#######################################################################
""".split('\n')
# Константы, используемые в этой программе:
EMPTY = ' '
START = 'S'
EXIT = 'E'
PATH = '.'
# Получаем высоту и ширину лабиринта:
HEIGHT = len(MAZE)
WIDTH = 0
for row in MAZE: # Устанавливаем WIDTH на ширину самой широкой строки.
if len(row) > WIDTH:
WIDTH = len(row)
# Преобразуем каждую строку лабиринта в список шириной WIDTH:
for i in range(len(MAZE)):
MAZE[i] = list(MAZE[i])
if len(MAZE[i]) != WIDTH:
MAZE[i] = [EMPTY] * WIDTH # Делаем эту строку пустой.
def printMaze(maze):
for y in range(HEIGHT):
# Печатаем каждую строку.
for x in range(WIDTH):
# Печатаем каждый столбец в этой строке.
print(maze[y][x], end='')
print() # Печатаем новую строку в конце строки.
print()
def findStart(maze):
for x in range(WIDTH):
for y in range(HEIGHT):
if maze[y][x] == START:
return (x, y) # Возвращаем координаты старта.
def solveMaze(maze, x=None, y=None, visited=None):
## ваш код
return False # БАЗОВЫЙ СЛУЧАЙ
Важно отметить, что в Python функции передают списки по ссылке. Это означает, что любые изменения в структуре данных лабиринта или списка посещенных точек сохраняются и после завершения рекурсивных вызовов.
#include <iostream>
#include <vector>
#include <string>
using namespace std;
// Создание структуры данных лабиринта
const string MAZE[] = {
"#######################################################################",
"#S# # # # # # # # # #",
"# ##### ######### # ### ### # # # # ### # # ##### # ### # # ##### # ###",
"# # # # # # # # # # # # # # # # # # # #",
"# # # ##### # ########### ### # ##### ##### ######### # # ##### ### # #",
"# # # # # # # # # # # # # # # # #",
"######### # # # ##### # ### # ########### ####### # # ##### ##### ### #",
"# # # # # # # # # # # # # # # # # #",
"# # ##### # # ### # # ####### # # # # # # # ##### ### ### ######### # #",
"# # # # # # # # # # # # # # # # # # #",
"### # # # # ### # # ##### ####### ########### # ### # ##### ##### ### #",
"# # # # # # # # # # # # # # # # #",
"# ### ####### ##### ### ### ####### ##### # ######### ### ### ##### ###",
"# # # # # # # # # # # # # # # # #",
"### ########### # ####### ####### ### # ##### # # ##### # # ### # ### #",
"# # # # # # # # # # # # # # # # # #",
"# ### # # ####### # ### ##### # ####### ### ### # # ####### # # # ### #",
"# # # # # # # # # E#",
"#######################################################################"
};
const char EMPTY = ' ';
const char START = 'S';
const char EXIT = 'E';
const char PATH = '.';
// Получаем высоту и ширину лабиринта:
const int HEIGHT = sizeof(MAZE) / sizeof(MAZE[0]);
int WIDTH = 0;
// Преобразуем лабиринт в двумерный вектор:
vector<vector<char>> maze(HEIGHT);
void initializeMaze() {
for (int i = 0; i < HEIGHT; i++) {
maze[i] = vector<char>(MAZE[i].begin(), MAZE[i].end());
if (MAZE[i].length() > WIDTH) {
WIDTH = MAZE[i].length();
}
}
// Устанавливаем пустые символы для строк, длина которых меньше максимальной ширины
for (int i = 0; i < HEIGHT; i++) {
while (maze[i].size() < WIDTH) {
maze[i].push_back(EMPTY);
}
}
}
void printMaze() {
for (int y = 0; y < HEIGHT; y++) {
for (int x = 0; x < WIDTH; x++) {
cout << maze[y][x];
}
cout << endl;
}
cout << endl;
}
pair<int, int> findStart() {
for (int y = 0; y < HEIGHT; y++) {
for (int x = 0; x < WIDTH; x++) {
if (maze[y][x] == START) {
return { x, y };
}
}
}
return { -1, -1 }; // Не найдено
}
bool solveMaze(int x, int y, vector<vector<bool>>& visited) {
// ваш код
}
int main() {
initializeMaze();
printMaze();
auto [startX, startY] = findStart();
if (startX == -1 || startY == -1) {
cout << "Start point not found!" << endl;
return 1;
}
vector<vector<bool>> visited(HEIGHT, vector<bool>(WIDTH, false));
if (solveMaze(startX, startY, visited)) {
cout << "Path found:" << endl;
}
else {
cout << "No path found!" << endl;
}
printMaze();
return 0;
}
Самопроверка
Парралелизация решения#
Важное: Прошу тех, кто выполняет работу на C++ в Visual Studio найти вкладку Отладка -> Свойства проекта -> Свойства конфигурации -> Общие-> Стандарт ISO C++17 (/std:c++17)
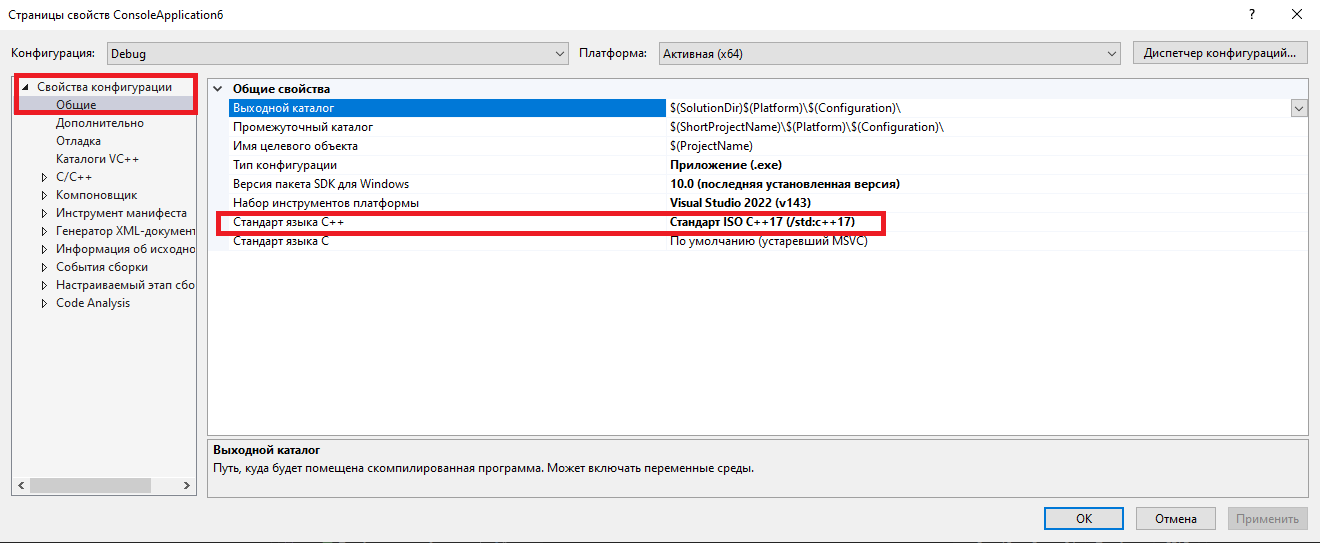
Цель: Переработать программу, использующую многозадачность для поиска пути в лабиринте с помощью потоков.
-
Изменение кода на использование потоков:
- Используйте библиотеку
threadingдля многозадачности. - Каждый рекурсивный вызов поиска пути должен выполняться в отдельном потоке.
- Используйте библиотеку
-
Работа с синхронизацией:
- Доверьте синхронизую GIL.
-
Использование массива посещённых клеток:
- Ведите учёт посещённых клеток с помощью двумерного массива, чтобы предотвратить многократное посещение одних и тех же клеток в разных потоках.
-
Параллельная проверка направлений:
- Программа должна параллельно проверять все возможные направления (север, юг, восток, запад) для каждой клетки и создавать отдельные потоки для каждого направления.
-
Завершение работы потоков:
- Потоки должны завершаться корректно.
- После завершения работы программы лабиринт должен быть выведен с помеченным путём, если путь найден.
-
Дополнительные улучшения:
- Добавьте ограничение на максимальное количество потоков, чтобы избежать слишком большого числа параллельных задач.
- Обработайте случай, когда путь не найден, и выведите соответствующее сообщение.
- Сделайте лабиринт изменяемым (например, позволяя пользователю задавать новые лабиринты или изменять размеры).
Ожидаемый результат:
- Программа должна корректно работать с многозадачностью.
- Лабиринт должен быть выведен на экран с помеченным путём, если он найден.
- Каждый поток должен обрабатывать одно направление для каждой клетки.
Цель: Переработать программу, использующую многозадачность для поиска пути в лабиринте с помощью потоков.
-
Изменение кода на использование потоков:
- Используйте библиотеку
threadingдля многозадачности. - Каждый рекурсивный вызов поиска пути должен выполняться в отдельном потоке.
- Используйте библиотеку
-
Работа с синхронизацией:
- Для синхронизации используйте
mutex
- Для синхронизации используйте
-
Использование массива посещённых клеток:
- Ведите учёт посещённых клеток с помощью двумерного массива, чтобы предотвратить многократное посещение одних и тех же клеток в разных потоках.
-
Параллельная проверка направлений:
- Программа должна параллельно проверять все возможные направления (север, юг, восток, запад) для каждой клетки и создавать отдельные потоки для каждого направления.
-
Завершение работы потоков:
- Потоки должны завершаться корректно.
- После завершения работы программы лабиринт должен быть выведен с помеченным путём, если путь найден.
-
Дополнительные улучшения:
- Добавьте ограничение на максимальное количество потоков, чтобы избежать слишком большого числа параллельных задач.
- Обработайте случай, когда путь не найден, и выведите соответствующее сообщение.
- Сделайте лабиринт изменяемым (например, позволяя пользователю задавать новые лабиринты или изменять размеры).
Ожидаемый результат:
- Программа должна корректно работать с многозадачностью.
- Лабиринт должен быть выведен на экран с помеченным путём, если он найден.
- Каждый поток должен обрабатывать одно направление для каждой клетки.
#include <iostream>
#include <vector>
#include <string>
#include <thread>
#include <mutex>
using namespace std;
// Создание структуры данных лабиринта
const string MAZE[] = {
"#######################################################################",
"#S# # # # # # # # # #",
"# ##### ######### # ### ### # # # # ### # # ##### # ### # # ##### # ###",
"# # # # # # # # # # # # # # # # # # # #",
"# # # ##### # ########### ### # ##### ##### ######### # # ##### ### # #",
"# # # # # # # # # # # # # # # # #",
"######### # # # ##### # ### # ########### ####### # # ##### ##### ### #",
"# # # # # # # # # # # # # # # # # #",
"# # ##### # # ### # # ####### # # # # # # # ##### ### ### ######### # #",
"# # # # # # # # # # # # # # # # # # #",
"### # # # # ### # # ##### ####### ########### # ### # ##### ##### ### #",
"# # # # # # # # # # # # # # # # #",
"# ### ####### ##### ### ### ####### ##### # ######### ### ### ##### ###",
"# # # # # # # # # # # # # # # # #",
"### ########### # ####### ####### ### # ##### # # ##### # # ### # ### #",
"# # # # # # # # # # # # # # # # # #",
"# ### # # ####### # ### ##### # ####### ### ### # # ####### # # ##### #",
"# # # # # # # # E#",
"#######################################################################"
};
const char EMPTY = ' ';
const char START = 'S';
const char EXIT = 'E';
const char PATH = '.';
// Получаем высоту и ширину лабиринта:
const int HEIGHT = sizeof(MAZE) / sizeof(MAZE[0]);
int WIDTH = 0;
// Преобразуем лабиринт в двумерный вектор:
vector<vector<char>> maze(HEIGHT);
mutex mazeMutex;
void initializeMaze() {
for (int i = 0; i < HEIGHT; i++) {
maze[i] = vector<char>(MAZE[i].begin(), MAZE[i].end());
if (MAZE[i].length() > WIDTH) {
WIDTH = MAZE[i].length();
}
}
// Устанавливаем пустые символы для строк, длина которых меньше максимальной ширины
for (int i = 0; i < HEIGHT; i++) {
while (maze[i].size() < WIDTH) {
maze[i].push_back(EMPTY);
}
}
}
void printMaze() {
lock_guard<mutex> lock(mazeMutex);
for (int y = 0; y < HEIGHT; y++) {
for (int x = 0; x < WIDTH; x++) {
cout << maze[y][x];
}
cout << endl;
}
cout << endl;
}
Cвязанные с темой индивидуальные проекты#
Вся литература находит на яндекс диске
Решатель «пятнашек»
264 стр - 293 стр Рекурсивная книга о рекурсии. — СПб.: Питер, 2023. — 336 с.: ил. — (Серия «Библиотека программиста»). ISBN 978-5-4461-2393-3
Генератор лабиринтов
248 стр - 264 сип Рекурсивная книга о рекурсии. — СПб.: Питер, 2023. — 336 с.: ил. — (Серия «Библиотека программиста»). ISBN 978-5-4461-2393-3
Для желающих продолжить#
Братец кролик нашел еще один древний дедушкин рецепт приготовления очень секретных и никому не нужных сообщений. Поэтому в одну из картинок, которую он заблаговременно пометил своим персональным знаком, он поместил целый архив с секретным txt файлом. Для извлечения информации вам потребуется
1. Скачать ту самую картинку
2. Переименовать расширение с *.jpg на *.rar
3. Разархивировать полученное
4. Прочитать инструкцию по методу приготовления подобных секретов
5. Прислать на почту картинку с архивом внутри
Повторение прошлого материала#
Определите алгоритм сортировки по его поведению
Вариант 1#
Дан массив: 7, 3, 9, 2, 5
Шаг 1: Сравниваем 7 и 3. Меняем местами, так как 7 > 3.
3, 7, 9, 2, 5
Шаг 2: Сравниваем 7 и 9. Не меняем местами, так как 7 < 9.
3, 7, 9, 2, 5
Шаг 3: Сравниваем 9 и 2. Меняем местами, так как 9 > 2.
3, 7, 2, 9, 5
Шаг 4: Сравниваем 9 и 5. Меняем местами, так как 9 > 5.
3, 7, 2, 5, 9
Шаг 5: Сравниваем 3 и 7. Не меняем местами, так как 3 < 7.
3, 7, 2, 5, 9
Шаг 6: Сравниваем 7 и 2. Меняем местами, так как 7 > 2.
3, 2, 7, 5, 9
Шаг 7: Сравниваем 7 и 5. Меняем местами, так как 7 > 5.
3, 2, 5, 7, 9
Шаг 8: Сравниваем 3 и 2. Меняем местами, так как 3 > 2.
2, 3, 5, 7, 9
Массив отсортирован: 2, 3, 5, 7, 9
Какой алгоритм сортировки использовался?
Вариант 2#
Дан массив: 34, 2, 10, 6, 7, 5
Шаги сортировки:
Начинаем с индекса 1 (элемент 2). Сравниваем 34 и 2. Меняем местами.
2, 34, 10, 6, 7, 5
Переходим к индексу 2 (элемент 10). Сравниваем 34 и 10. Меняем местами.
2, 10, 34, 6, 7, 5
Переходим к индексу 3 (элемент 6). Сравниваем 34 и 6. Меняем местами.
2, 10, 6, 34, 7, 5
Переходим к индексу 4 (элемент 7). Сравниваем 34 и 7. Меняем местами.
2, 10, 6, 7, 34, 5
Переходим к индексу 5 (элемент 5). Сравниваем 34 и 5. Меняем местами.
2, 10, 6, 7, 5, 34
Переходим к индексу 4 (элемент 5). Сравниваем 7 и 5. Меняем местами.
2, 10, 6, 5, 7, 34
Переходим к индексу 3 (элемент 5). Сравниваем 6 и 5. Меняем местами.
2, 10, 5, 6, 7, 34
Переходим к индексу 2 (элемент 5). Сравниваем 10 и 5. Меняем местами.
2, 5, 10, 6, 7, 34
Переходим к индексу 1 (элемент 5). Сравниваем 2 и 5. Процесс завершен, массив отсортирован.
2, 5, 6, 7, 10, 34
Вариант 3#
Дан массив: 10, 80, 30, 90, 40, 50, 70
Шаги быстрой сортировки:
Выбираем опорный элемент (например, 50). Разделяем массив на две части:
Левые: 10, 30, 40
Правые: 80, 90, 70
Сортируем левую часть (опорный элемент 30):
Левые: 10
Правые: 40
Массив после сортировки: 10, 30, 40
Сортируем правую часть (опорный элемент 80):
Левые: 70
Правые: 90
Массив после сортировки: 70, 80, 90
Собираем отсортированные части: 10, 30, 40, 50, 70, 80, 90
Какой алгоритм сортировки использовался?
Вариант 4#
Шаг 1: Формирование списков по единицам:
Список 1 (элементы, заканчивающиеся на 0, 2): 170, 802
Список 2 (элементы, заканчивающиеся на 5, 6): 45, 75, 66
Список 3 (элементы, заканчивающиеся на 4, 9): 90, 24
Список 4 (элементы, заканчивающиеся на 2): 2
Шаг 2: Формирование новых списков по десяткам:
Список 1 (элементы с десятками 0): 802, 2
Список 2 (элементы с десятками 2): 24
Список 3 (элементы с десятками 4): 45
Список 4 (элементы с десятками 5): 75
Список 5 (элементы с десятками 6): 66
Список 6 (элементы с десятками 7): 170
Список 7 (элементы с десятками 9): 90
Шаг 3: Формирование новых списков по сотням:
Список 1 (элементы с сотнями 0): 2, 24, 45, 66, 75, 90
Список 2 (элементы с сотнями 1): 170
Список 3 (элементы с сотнями 8): 802
Шаг 4: Объединение всех списков в итоговый отсортированный массив:
Итоговый отсортированный массив: 2, 24, 45, 66, 75, 90, 170, 802