ДЗ Лабораторная работа №3 "Алгоритмы сортировки"#
Warning
За задание можно получить до 5 баллов, соблюдая следующие условия:
- Написано на C++ ( + 1 балл)
- Тестрование проводилось с использованием Unit-test ( + 1 балл)
- Задание зачтено ( +3 балла)
В отчете должно быть указано следующие:
1. Титульный лист, где указаны ФИО преподавателя, номер задания, номер варианта
2. Формулировка задания
3. Ссылка на github-репозиторий с работающим кодом
4. Блок-схема каждого алгоритма отдельно с описанием алгоритма
5. После каждого описания идет листинг кода
6. Пример входных и выходных данных (таблицей)
7. Произвести асимптотическую оценку (лучший случай, худший случай, средний случай)
8. В конце работы приводятся реальные замеры на вашем ЭВМ в виде таблицы и графика
Примечание 1: Для реализации Unit-test рекомендуется произвести тестрование при помощи assertEqual и Assert::Is
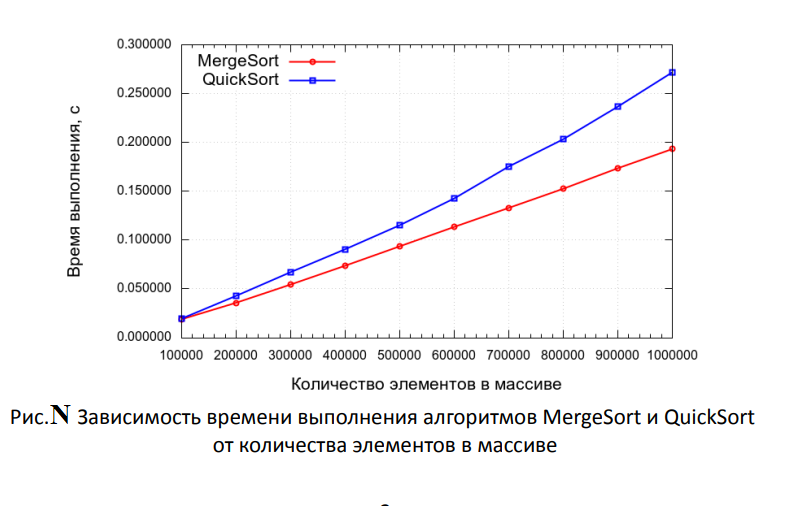
Примечание 2: Оси графиков должны быть подписаны — указаны название показателя и единицы его измерения. Например, «Время выполнения алгоритмы, с», «Количество элементов в массиве». Под графиком размещается подрисуночная подпись с пояснением зависимость какой величины от какого параметра на нем показана.
Описания алгоритмов#
Для реализации ниже дано словесное описание алгоритма и его псевдокод. Блок-схемы составляете самостоятельно, например, при помощи сервиса programforyou
Сортировка пузырьком#
Сортировка пузырьком — это простейший и один из самых известных алгоритмов сортировки. Идея заключается в последовательном сравнении значений соседних элементов. Если текущий элемент больше следующего, меняем их местами. Алгоритм необходимо повторять до тех пор, пока массив не будет отсортирован.
Функция пузырьковаяСортировка(массив):
n ← длина(массив)
для i от 0 до n - 2:
для j от 0 до n - 2:
если массив[j] > массив[j + 1] то:
поменять местами(массив[j], массив[j + 1])
конец если
конец внутреннего цикла
конец внешнего циикла
конец функции
Гномья сортировка#
Гномья сортировка — это алгоритм сортировки, основанный на идее, что мы можем перемещать элементы в массиве, как будто "гуляем" по нему, начиная с конца. Если текущий элемент больше следующего, то они меняются местами и продолжаем двигаться назад, пока не окажемся на месте, где элементы расположены в правильном порядке.
Гномья сортировка основана на технике, используемой обычным голландским садовым гномом (нидерл. tuinkabouter). Это метод, которым садовый гном сортирует линию цветочных горшков. По существу он смотрит на текущий и предыдущий садовые горшки: если они в правильном порядке, он шагает на один горшок вперёд, иначе он меняет их местами и шагает на один горшок назад. Граничные условия: если нет предыдущего горшка, он шагает вперёд; если нет следующего горшка, он закончил.
Функция гномьяСортировка(массив):
i ← 1
пока i < длина(массив):
если i > 0 и массив[i - 1] > массив[i] то:
поменять местами(массив[i - 1], массив[i])
i ← i - 1
иначе:
i ← i + 1
конец цикла
конец функции
Сортировка расческой#
Сортировка расческой — модификация пузырьковой сортировки, основанной на сравнении элементов на расстоянии.
Сортировка расческой — это улучшение сортировки пузырьком. Основная идея заключается в том, чтобы с каждым шагом уменьшать интервал, на котором происходят сравнения и обмены элементов, а не всегда сравнивать только соседние элементы, как в сортировке пузырьком. Начинаем с большого интервала (расстояния) между сравниваемыми элементами и постепенно уменьшаем его. Алгоритм продолжает работать до тех пор, пока не произойдут обмены на самом маленьком интервале, что гарантирует завершение сортировки.
Функция сортировкаРасческой(массив):
n ← длина(массив)
шаг ← n - 1 # Начальный шаг
пока шаг > 1:
шаг ← шаг // 1.3 # Уменьшаем шаг
i ← 0
пока i + шаг < n:
если массив[i] > массив[i + шаг] то:
поменять местами(массив[i], массив[i + шаг])
конец если
i ← i + 1
конец цикла
конец цикла
конец функции
Сортировка слиянием#
Сортировка слиянием — это эффективный алгоритм сортировки, который использует метод "разделяй и властвуй". Алгоритм рекурсивно делит массив на два подмассива, сортирует их и затем сливает их обратно в один отсортированный массив. Это деление продолжается до тех пор, пока каждый подмассив не станет содержать только один элемент, после чего начинается процесс слияния.
Функция сортировкаСлиянием(массив):
если длина(массив) > 1 то:
середина ← длина(массив) // 2
леваяПоловина ← массив[0:середина]
праваяПоловина ← массив[середина:конец]
сортировкаСлиянием(леваяПоловина)
сортировкаСлиянием(праваяПоловина)
i ← 0 # Индекс для левой половины
j ← 0 # Индекс для правой половины
k ← 0 # Индекс для исходного массива
пока i < длина(леваяПоловина) и j < длина(праваяПоловина):
если леваяПоловина[i] < праваяПоловина[j] то:
массив[k] ← леваяПоловина[i]
i ← i + 1
иначе:
массив[k] ← праваяПоловина[j]
j ← j + 1
конец если
k ← k + 1
пока i < длина(леваяПоловина):
массив[k] ← леваяПоловина[i]
i ← i + 1
k ← k + 1
пока j < длина(праваяПоловина):
массив[k] ← праваяПоловина[j]
j ← j + 1
к ← к + 1
конец если
конец функции
Сортировка вставками#
Сортировка вставками — это один из простейших алгоритмов сортировки, который работает по принципу пошагового построения отсортированной части массива, где каждый новый элемент вставляется в нужное место в уже отсортированной части. Этот алгоритм эффективно работает на малых объемах данных, но его производительность значительно ухудшается на больших объемах.
Идея работы алгоритма:
- Начинаем с второго элемента массива и сравниваем его с предыдущим.
- Если текущий элемент меньше предыдущего, перемещаем его на нужную позицию в отсортированную часть массива, сдвигая остальные элементы вправо.
- Повторяем эти шаги для всех элементов массива, постепенно расширяя отсортированную часть.
Функция сортировкаВставками(массив):
для i от 1 до длина(массив) - 1:
текущий ← массив[i]
j ← i - 1
пока j >= 0 и массив[j] > текущий:
массив[j + 1] ← массив[j]
j ← j - 1
конец пока
массив[j + 1] ← текущий
конец цикла
конец функции
Сортировка Шелла#
Сортировка Шелла — это улучшение сортировки вставками, которое делает ее более эффективной за счет использования шагов для сравнения и перемещения элементов, что позволяет значительно ускорить процесс сортировки. В отличие от стандартной сортировки вставками, которая сравнивает только соседние элементы, сортировка Шелла использует интервалы (шаги) между элементами для более быстрого сдвига элементов в правильное положение.
Идея заключается в том, чтобы сначала отсортировать элементы с большими интервалами, а затем постепенно уменьшать шаг, пока не достигнем единичного шага, что приведет к окончательной сортировке.
Функция сортировкаШелла(массив):
n ← длина(массив)
шаг ← n // 2 # Начальный шаг
пока шаг > 0:
для i от шаг до n - 1:
временный ← массив[i]
j ← i
пока j >= шаг и массив[j - шаг] > временный:
массив[j] ← массив[j - шаг]
j ← j - шаг
конец пока
массив[j] ← временный
конец цикла
шаг ← шаг // 2 # Уменьшаем шаг
конец цикла
конец функции
Поразрядная сортировка#
Поразрядная сортировка (Radix Sort) — это алгоритм сортировки, который работает путем обработки элементов по разрядам (цифрам, буквам и т. д.), начиная с наименее значимого разряда (или наоборот — с наиболее значимого).
Основные этапы алгоритма:
- Алгоритм обрабатывает числа или строки по разрядам.
- Сортирует элементы на каждом разряде с использованием другого алгоритма сортировки (чаще всего сортировки подсчетом).
- Повторяет процесс для каждого разряда, начиная с младшего и заканчивая старшим.
- После завершения сортировки элементов по всем разрядам массив становится отсортированным.
Функция поразряднаяСортировка(массив):
максимальноеЧисло ← максимальное(массив)
разряд ← 1
пока максимальноеЧисло // разряд > 0:
сортироватьПоРазряду(массив, разряд)
разряд ← разряд * 10
конец цикла
конец функции
Функция сортироватьПоРазряду(массив, разряд):
# Используем сортировку по подсчету для данного разряда
корзины ← [пустой список для 10 разрядов]
для числа в массиве:
индексКорзины ← (число // разряд) % 10
корзины[индексКорзины].добавить(число)
конец цикла
массив ← объединитьКорзины(корзины)
конец функции
Функция объединитьКорзины(корзины):
объединенныйМассив ← пустой список
для корзины в корзинах:
объединенныйМассив.расширить(корзина)
конец цикла
вернуть объединенныйМассив
Быстрая сортировка#
Быстрая сортировка (Quick Sort) — это один из самых быстрых алгоритмов сортировки. Она также использует метод "разделяй и властвуй", но отличается от сортировки слиянием тем, что данные не нужно копировать в дополнительные массивы. Алгоритм основывается на выборе опорного элемента, который затем используется для разделения массива на две части — элементы меньшие опорного и элементы большие опорного. После этого рекурсивно сортируются эти части.
Основные этапы алгоритма:
- Выбирается опорный элемент.
- Массив переставляется так, чтобы все элементы, меньшие опорного, оказались слева от него, а все элементы, большие — справа.
- Рекурсивно повторяем сортировку для левой и правой части массива.
Функция быстраяСортировка(массив, низ, высокий):
если низ < высокий то:
опорныйИндекс ← разделить(массив, низ, высокий)
быстраяСортировка(массив, низ, опорныйИндекс - 1)
быстраяСортировка(массив, опорныйИндекс + 1, высокий)
конец если
Функция разделить(массив, низ, высокий):
опорный ← массив[высокий]
i ← низ - 1
для j от низ до высокий - 1:
если массив[j] <= опорный то:
i ← i + 1
поменять местами(массив[i], массив[j])
поменять местами(массив[i + 1], массив[высокий])
вернуть i + 1
Варианты#
| № | Алгоритм 1 | Алгоритм 2 | Алгоритм 3 |
|---|---|---|---|
| 1 | Поразрядная сортировка | Гномья сортировка | Быстрая сортировка |
| 2 | Сортировка пузырьком | Поразрядная сортировка | Быстрая сортировка |
| 3 | Поразрядная сортировка | Сортировка слиянием | Быстрая сортировка |
| 4 | Поразрядная сортировка | Сортировка расческой | Быстрая сортировка |
| 5 | Сортировка Шелла | Поразрядная сортировка | Быстрая сортировка |
| 6 | Сортировка вставками | Поразрядная сортировка | Быстрая сортировка |
| 7 | Поразрядная сортировка | Сортировка пузырьком | Быстрая сортировка |
| 8 | Сортировка слиянием | Поразрядная сортировка | Быстрая сортировка |
| 9 | Поразрядная сортировка | Сортировка Шелла | Быстрая сортировка |
| 10 | Гномья сортировка | Поразрядная сортировка | Быстрая сортировка |
| 11 | Сортировка пузырьком | Сортировка слиянием | Быстрая сортировка |
| 12 | Сортировка расческой | Сортировка Шелла | Быстрая сортировка |
| 13 | Сортировка вставками | Сортировка пузырьком | Быстрая сортировка |
| 14 | Сортировка слиянием | Сортировка расческой | Быстрая сортировка |
| 15 | Сортировка Шелла | Сортировка вставками | Быстрая сортировка |
| 16 | Поразрядная сортировка | Поразрядная сортировка | Быстрая сортировка |
| 17 | Поразрядная сортировка | Сортировка пузырьком | Быстрая сортировка |
| 18 | Сортировка слиянием | Поразрядная сортировка | Быстрая сортировка |
| 19 | Поразрядная сортировка | Сортировка Шелла | Быстрая сортировка |
| 20 | Сортировка вставками | Поразрядная сортировка | Быстрая сортировка |
| 21 | Поразрядная сортировка | Гномья сортировка | Быстрая сортировка |
| 22 | Поразрядная сортировка | Сортировка пузырьком | Быстрая сортировка |
| 23 | Сортировка слиянием | Поразрядная сортировка | Быстрая сортировка |
| 24 | Поразрядная сортировка | Сортировка расческой | Быстрая сортировка |
| 25 | Сортировка Шелла | Поразрядная сортировка | Быстрая сортировка |
| 26 | Поразрядная сортировка | Сортировка вставками | Быстрая сортировка |
| 27 | Поразрядная сортировка | Сортировка слиянием | Быстрая сортировка |
| 28 | Сортировка пузырьком | Поразрядная сортировка | Быстрая сортировка |
| 29 | Поразрядная сортировка | Сортировка Шелла | Быстрая сортировка |
| 30 | Гномья сортировка | Поразрядная сортировка | Быстрая сортировка |