Практика 4 Методы оптимизации "Разделяй и влавствуй"

Одна большая задача может казаться трудной. Но если разделить её на две задачи в два раза меньше, она станет намного проще. Для таких случаев хорошо подходят алгоритмы «разделяй и властвуй». Они так и работают: разделяют задачу на более мелкие подзадачи, независимо находят решения для них и соединяют результаты в решение изначальной задачи.

Конечно, реальные ситуации бывают более сложными, чем мы описали. После разделения одной задачи на подзадачи, алгоритм обычно делит их на ещё более мелкие под-подзадачи и так далее. Он продолжает это делать, пока не дойдёт до точки, где в рекурсии уже нет необходимости.

Важнейший шаг в работе с алгоритмами «разделяй и властвуй» — это соединить решения подзадач в решение изначальной задачи.

ПАРАДИГМА РАЗДЕЛЯЙ И ВЛАСТВУЙ

1. Разделить входные данные на более мелкие подзадачи.
2. Решить подзадачи рекурсивным методом.
3. Объединить решения подзадач в решение исходной задач

Бинарное возведение в степень

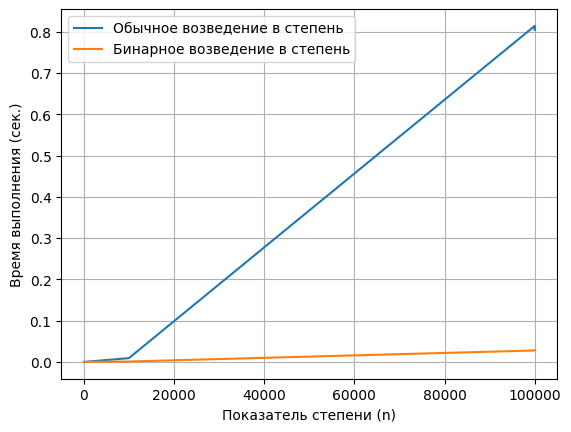
Бинарное возведение в степень — приём, позволяющий возводить любое число в $n$-ую степень за $O(\log n)$ умножений (вместо $n$ умножений при обычном подходе).

Заметим, что для любого числа $a$ и чётного числа $n$ выполняется тождество:

$$a^n = (a^{n/2})^2 = a^{n/2} \cdot a^{n/2}$$

Получается, что для любого чётного $n$ мы можем свести задачу к вдвое меньшей ($n' = \frac{n}{2}$), потратив всего одну операцию умножения.

Если же $n$ нечётно, то верно следующее:

$$a^n = a^{n-1} \cdot a$$

Получается, для нечётных $n$ мы можем сделать сведение к задаче размера $(n-1)$, которая уже будет чётной.

Мы фактически нашли рекуррентную формулу для подсчёта $a^n$:

$$a^n = f(a, n) = \begin{cases} 1, & n = 0 \\ f(a, \frac{n}{2})^2, & 2 \mid n \\ f(a, n - 1) \cdot a, & 2 \nmid n \end{cases}$$

Так как каждые два перехода $n$ гарантированно уменьшается хотя бы в два раза, всего будет не более $2 \cdot \log_2 n$ переходов, прежде чем мы придём к $n = 0$. Каждый переход требует ровно одно умножение, и таким образом, мы получили алгоритм, работающий за $O(\log n)$ умножений.

Сразу напрашивается рекурсивная реализация этого алгоритма:

PythonC++

    def binpow(a, n):
        if n == 0:
            return 1
        if n % 2 == 1:
            return binpow(a, n - 1) * a
        else:
            b = binpow(a, n // 2)
            return b * b

    int binpow(int a, int n) {
        if (n == 0)
            return 1;
        if (n % 2 == 1)
            return binpow(a, n - 1) * a;
        else {
            int b = binpow(a, n / 2);
            return b * b;
        }
    }

Наша рекурсия хороша всем, кроме того, что затраты на её построение многократно больше, чем проведение самих операций. Попробуем «развернуть» рекурсию и получить итеративную.

Рассмотрим двоичное представление числа $n$. Результат $a^n$ можно представить как произведение $a$ в степенях каких-то степеней двоек. Например, если $n = 42 = 32 + 8 + 2$, то

$$a^{42} = a^{32+8+2} = a^{32} \cdot a^8 \cdot a^2$$

Чтобы посчитать это произведение итеративно, пройдемся по всем битам числа $n$, поддерживая две переменные: непосредственно результат и текущее значение $a^{2^k}$, где $k$ — это номер текущей итерации.

На каждом шаге будем домножать $a^{2^k}$ на текущий результат, если $k$-тый бит числа $n$ единичный, и в любом случае возводить её в квадрат, получая

$$a^{2^k \cdot 2} = a^{2^{k+1}}$$

для следующей итерации.

Посмотрим на поведение алгоритма в режиме реального времени при помощи следующей реализации на js:

Наконец реализуем сами подобную функцию и проверим её корректность:

PythonC++

    def binpow(a, n):
        res = 1
        while n != 0:
            if n & 1:  # Если показатель степени нечётный
                res *= a
            a *= a  # Умножаем основание на себя
            n >>= 1  # Сдвигаем показатель степени на 1 вправо
        return res

    int binpow(int a, int n) {
        int res = 1;
        while (n != 0) {
            if (n & 1) // если показатель степени нечетный
                res = res * a;
            a = a * a; // Умножаем основание на себя
            n >>= 1; // Сдвигаем показатель степени на 1 вправо
        }
        return res;
    }

Note

Стоит отметить, что во многих языках программирования бинарное возведение в степень уже реализовано. 
Однако в C++ это не так: функция `pow` из стандартной библиотеки реализована только для действительных чисел и использует приближенные методы, поэтому не дает точных результатов для целочисленных аргументов.

Обобщение

Бинарное возведение в степень применимо не только к умножению чисел, но и к любым ассоциативным операциям — таким, для которых для любых $a$, $b$ и $c$ выполняется:

$$(a \circ b) \circ c = a \circ (b \circ c)$$

Наиболее очевидное обобщение — на остатки по модулю:

$a^n \mod b$

Дополните функцию таким образом, чтобы она считала при помощи данного трюка формулу выше. Обратите внимание, что операция взятия остатка ассоциативна, следовательно, от вас не потребуется изменять существенно код.

Вторым самым «популярным» обобщением является произведение матриц, однако работа с ними выходит за рамки нашего ознакомительного курса.

Алгоритм Карацубы

В 1960-м году Андрей Колмогоров вместе с другими пионерами советской информатики собрались на научном семинаре и выдвинули «гипотезу $n^2$»: невозможно перемножить два $n$-значных числа быстрее, чем за $O(n^2)$. Это подразумевает, что умножение «в столбик», придуманное шумерами как минимум четыре тысячи лет назад и никем на тот момент не побитое, является асимптотически оптимальным алгоритмом умножения двух чисел.

Через неделю 23-летний аспирант Анатолий Карацуба предложил метод умножения с оценкой времени работы $O(n^{\log_2 3})$ и тем самым опроверг гипотезу.

Основная идея алгоритма очень простая: в нём умножение двух чисел длины $n$ небольшим алгебраическим трюком сводится к трём умножениям чисел длины $\frac{n}{2}$. Число элементов на каждом уровне рекурсии будет расти, но на самом нижнем будет суммарно всего $O(n^{\log_2 3})$ элементов, чем и объясняется такая странная асимптотика.

Умножение многочленов

В нашей версии алгоритма мы будем перемножать не числа, а многочлены. Любое число можно можно представить в виде многочлена, если вместо x подставить основание системы счисления, а в качестве коэффициентов можно взять последовательность цифр числа:

$$A(x) = a_0 + a_1 \cdot x + a_2 \cdot x^2 + \dots + a_n \cdot x^n$$
$$= a_0 + a_1 \cdot 10 + a_2 \cdot 10^2 + \dots + a_n \cdot 10^n$$

Реализуем функцию перевода числа в такое представление чуть позже. Перед этим поговорим про еще один способ оценки алгоритма.

Мастер-теорема

Основная схема алгоритма очень простая: в нём умножение двух чисел длины $n$ небольшим алгебраическим трюком сводится к трём умножениям чисел длины $\frac{n}{2}$. Примечательно, что нужные формулы были ещё у Чарльза Бэббиджа, работавшего в начале XIX века над механическим компьютером для подсчета налогов для британской короны, однако он не обратил внимания на возможность использования лишь трёх рекурсивных умножений вместо четырех.

То, почему он работает за такую странную асимптотику, весьма неочевидно, и для этого мы сначала докажем более мощную теорему, которая говорит об асимптотике большого класса алгоритмов вида «разделяй-и-властвуй», заменяющих исходную задачу на $a$ задач размера $\frac{n}{b}$.

Мастер-теорема. Пусть имеется рекуррента:

$$T(n) = \begin{cases} a T\left(\frac{n}{b}\right) + \Theta(n^c), & n > n_0 \\ \Theta(1), & n \leq n_0 \end{cases}$$

Тогда:

• A. Если $c > \log_b a$, то $T(n) = \Theta(n^c)$.
• B. Если $c = \log_b a$, то $T(n) = \Theta(n^c \log n)$.
• C. Если $c < \log_b a$, то $T(n) = \Theta(n^{\log_b a})$.

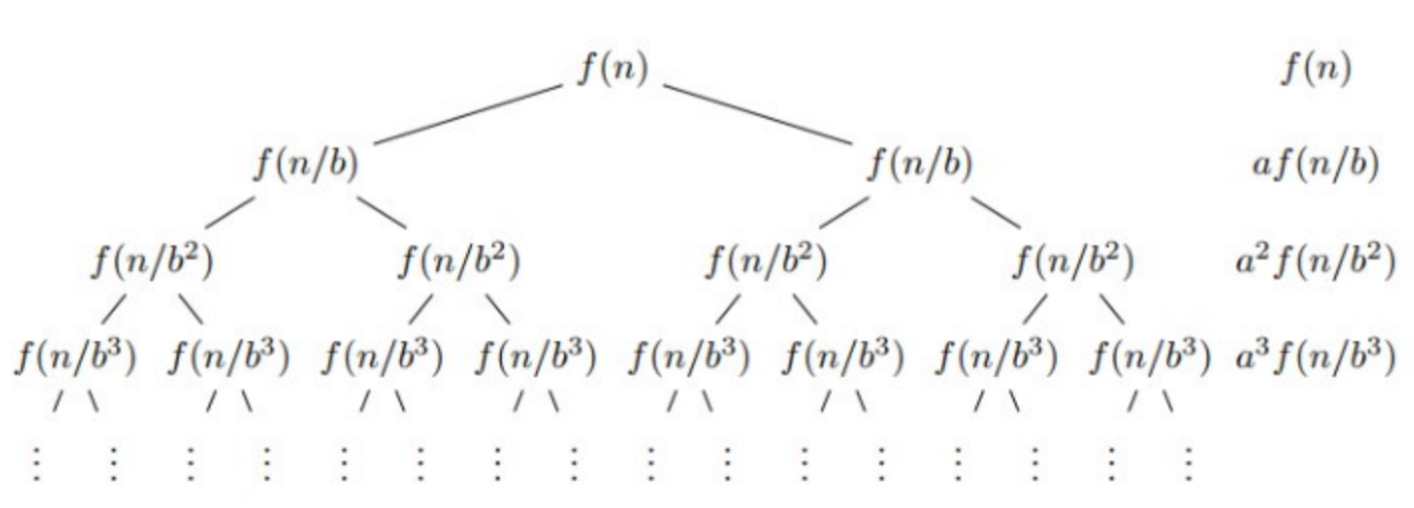
Доказательство. Рассмотрим «дерево рекурсии» этого соотношения. В нём будет $\log_b n$ уровней. На $k$-том уровне будет $a^k$ вершин, каждая из которых будет стоить $\left(\frac{n}{b^k}\right)^c$ операций. Просуммируем значения во всех вершинах по всем уровням:

$$T(n) = \sum_{k=0}^{\log_b n} a^k \left(\frac{n}{b^k}\right)^c = n^c \sum_{k=0}^{\log_b n} \left(\frac{a}{b^c}\right)^k$$

A. Если $c > \log_b a$, то $\sum \left(\frac{a}{b^c}\right)^k$ — это сумма убывающей геометрической прогрессии, которая не зависит от $n$ и просто равна какой-то константе. Значит, $T(n) = \Theta(n^c)$.

B. Если $c = \log_b a$, то

$$T(n) = n^c \sum_{k=0}^{\log_b n} \left(\frac{a}{b^c}\right)^k = n^c \sum_{k=0}^{\log_b n} 1^k = \Theta(n^c \log_b n)$$

C. Если $c < \log_b a$, то так как сумма прогрессии асимптотически эквивалентна своему старшему элементу,

$$T(n) = n^c \sum_{k=0}^{\log_b n} \left(\frac{a}{b^c}\right)^k = \Theta\left(n^c \left(\frac{a}{b^c}\right)^{\log_b n}\right) = \Theta\left(n^c \cdot \frac{a^{\log_b n}}{n^c}\right) = \Theta\left(a^{\log_b n}\right) = \Theta(n^{\log_b a})$$

Примечание. Для более точных оценок асимптотики «мерджа» теорема ничего не говорит. Например, если мердж занимает $\Theta(n \log n)$ и задача разбивается каждый раз на две части, то асимптота будет равна:

$$\sum_{k=0}^{\log n} n \log \frac{n}{2^k} = \sum_{k=0}^{\log n} n (\log n - k) = n \sum_{k=0}^{\log n} k = \Theta(n \log^2 n)$$

В то же время эта рекуррента под условия теоремы не попадает. Можно лишь получить неточные границы $\Omega(n \log n)$ и $O(n^{1+\epsilon})$, если подставить $c = 1$ и $c = 1 + \epsilon$ соответственно. Заметим, что $n \log n$ и $n \log^2 n$ асимптотически меньше $n^{1+\epsilon}$, каким бы маленьким $\epsilon$ ни был.

Примененеие Мастер-теоремы для оценки Алгоритма Карацубы

Пусть у нас есть два многочлена $a(x)$ и $b(x)$ длины $n = 2k$, и мы хотим их перемножить. Разделим их коэффициенты на две равные части и представим как:

$$a(x) = a_1(x) + x^k a_2(x)$$
$$b(x) = b_1(x) + x^k b_2(x)$$

Теперь рекурсивно вычислим многочлены-произведения $p_1$ и $p_2$:

$$p_1(x) = a_1(x) \cdot b_1(x)$$
$$p_2(x) = a_2(x) \cdot b_2(x)$$

А также многочлен $t$:

$$t(x) = (a_1(x) + a_2(x)) \cdot (b_1(x) + b_2(x))$$

Результат умножения исходных многочленов теперь можно посчитать по следующей формуле — внимание, алгебра:

$$c(x) = a(x) \cdot b(x) = p_1(x) + x^k \cdot (t(x) - p_1(x) - p_2(x)) + x^{2k} \cdot p_2(x)$$

Корректность формулы можно проверить, просто выполнив нужные подстановки.

Обратим внимание, что результат умножения — многочлен размера $2n$.

Анализ

Если посчитать необходимые операции, то выясняется, что для перемножения двух многочленов размера /n/ нам нужно посчитать три произведения — /p_1/, /p_2/ и /t/ — размера /n/2/ и константное количество сложений, вычитаний и сдвигов (домножений на /x^k/), которые суммарно можно выполнить за /O(n)/.

Пролистав пол-экрана выше, можно убедиться, что асимптотика всего алгоритма будет /Theta(n^{log_2 3}) ≈ Theta(n^{1.58})/: в данном случае наша задача разбивается на /a = 3/ части в /b = 2/ раз меньшего размера, а объединение происходит за /O(n)/.

Реализация

Для простоты будем предполагать, что /n/ это степень двойки. Если это не так, то в зависимости от обстоятельств это можно исправить одним из двух костылей:

1. Можно дополнить коэффициенты многочлена нулями до ближайшей степени двойки — в худшем случае это будет работать в /2^{1.58} ≈ 3/ раза дольше.
2. Можно «отщепить» последний коэффициент от многочленов и свести задачу размера /2k + 1/ к задаче размера /2k/ и константному количеству сложений.

В этой статье мы будем использовать первый метод.

Основные соображения по поводу эффективной реализации:

• Нужно выделять как можно меньше лишней памяти, для чего нужно переиспользовать имеющиеся массивы.
• Все арифметические операции нужно реализовать как простые линейные проходы по массивам, чтобы компилятор смог их векторизовать.
• Вместо использования базы вида if (n == 1) c[0] = a[0] * b[0], имеет смысл, начиная с какого-то размера задачи, использовать более эффективное наивное умножение за квадрат.

Выделение массива, инциализация нулями С++

const int k = 2;
new int[k]() // массив размер 2 [0,0]

Алтернативно:

int a[65] = { 0 };  // массив размер 65

Код основной рекурсивной процедуры:

PythonC++

def karatsuba(a, b, n):
    c = [0] * (2 * n)  # Размер результата всегда 2 * n

    if n <= 64:
        # Базовый случай: обычное умножение
        for i in range(n):
            for j in range(n):
                c[i + j] += a[i] * b[j]
    else:
        k = n // 2
        l = [0] * k
        r = [0] * k
        t = [0] * n

        for i in range(k):
            l[i] = a[i] + a[k + i]
            r[i] = b[i] + b[k + i]

        # Рекурсивные вычисления для t, p1, p2
        t = karatsuba(l, r, k)  
        p1 = karatsuba(a, b, k)  
        p2 = karatsuba(a[k:], b[k:], k) 

        t1 = t[:k]
        t2 = t[k:]
        s1 = p1[:k]
        s2 = p1[k:2*k]
        s3 = p2[:k]
        s4 = p2[k:2*k]

        # Применяем корректные сдвиги
        for i in range(k):
            c1 = s2[i] + t1[i] - s1[i] - s3[i]
            c2 = s3[i] + t2[i] - s2[i] - s4[i]
            c[k + i] += c1  # сдвиг для второго произведения
            c[n + i] += c2  # сдвиг для третьего произведения

    return c  # возвращаем результат

void karatsuba(int* a, int* b, int* c, int n) {
    if (n <= 64) {
        // Base case: direct multiplication for small arrays
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                c[i + j] += a[i] * b[j];
            }
        }
    }
    else {
        const int k = n / 2;


        int* l = new int[k]();
        int* r = new int[k]();
        int* t = new int[n]();


        for (int i = 0; i < k; i++) {
            l[i] = a[i] + a[k + i];
            r[i] = b[i] + b[k + i];
        }


        karatsuba(l, r, t, k);  // t = (a + b) * (a + b)
        karatsuba(a, b, c, k);   // c = a * b
        karatsuba(a + k, b + k, c + n, k);  // c = (a + k) * (b + k)


        for (int i = 0; i < k; i++) {
            int c1 = c[i + k] + t[i] - c[i] - c[i + 2 * k];
            int c2 = c[i + 2 * k] + t[i + k] - c[i + k] - c[i + 3 * k];


            if (c1 >= 10) {
                c1 -= 10;  
                c[k + i + 1] += 1; 
            }

            if (c2 >= 10) {
                c2 -= 10;  
                c[k + i + 2] += 1;  
            }

            c[k + i] = c1;
            c[n + i] = c2;
        }


        delete[] l;
        delete[] r;
        delete[] t;
    }
}

После трёх рекурсивных вызовов массив $c$ — это конкатенация $p_1$ и $p_2$.

После этого, для подсчёта самого многочлена $c$ проще всего мысленно разделить его на четыре равные части, а многочлен $t$ — на две половины $t_1$ и $t_2$, а затем посмотреть на формулу и подумать, как изменится каждая часть:

• $s_1$: не меняется — это первая половина $p_1$.
• $s_2$: выражается как $s_2 + t_1 - s_1 - s_3$, то есть изменяется на «первую» половину $t - p_1 - p_2$.
• $s_3$: выражается как $s_3 + t_2 - s_2 - s_4$, то есть изменяется на «вторую» половину $t - p_1 - p_2$.
• $s_4$: не меняется — это вторая половина $p_2$.

Task

- Реализовать метод to_number() принимающий на вход  массив со значениями разложения и основание и число'
- Реализовать метод to_polinom() принимающий на вход число и основание и возвращющий массив со значениями разложения'
- Реализовать метод carry_over() исправляющий массив после алгоритма карацубы для Python, этот метод переводит массив примерно по такому правилу (перенос разрядов): [64,0,0] в [6,4,0,0]'
- Реализовать метод print_large_number() для программистов на С++ для вывода массива без пропусков;

Проблема с большими числами в Python

Python начинает себя плохо чувствовать при очень больших числах.
Например, при умножени 10^65 *10^65 у него выйдет 10000000000000000597830782460516151851749290252338090708736359498322008205751130936310560341066601403445681992244323541365884452864
Очевидно, что это неверный ответ и связан с известными нами эффектами ошибок округления.
По этой причне рекуомендуемые вараинты a и b следующие
a = 9**67 
b = 9**67
Ответ 73874790939762171563984554767672159520401727385386379365358192581197851301497627794324640971004103380045519482931909029097635840
a = 9**66 
b = 9**66
Ответ 12034456046446549528857749197467573159437284243992482729042107040377150921373735159197502711845934670473681562413951491244032

Домашнее задание

Воспользуйтесь мастер-теоремой и оцените алгоритм бинарного вовзедения в степень
Повторите как объявлять массивы в С++ И Python, заполнять их случайными числами,  выводить в консоль. Определите, какими командами вы хотите работать на паре.

Примечание для желающих продолжить

Братец кролик продолжает тестировать все поряд. Особенно он любит вбивать вместо чисел какие-нибудь буквы. Когда-то давно братец кролик читал медицинский трактат De Medicina Praecepta Саммоника, врача императора Септимия Севера, где вычитал оригинальный рецепт лечения сенной лихорадки при помощи заклинания. Слово abracadabra предписывалось использовать следующим образом: оно выписывалось столбиком на дощечке 11 раз, при этом последняя буква каждый раз отсекалась. Получался треугольник. Такое постепенное укорачивание этого слова должно было уничтожать силу злого духа, и больной, надевая амулет, должен был постепенно выздоравливать. В большинстве современных языков слово приобрело значение полной бессмыслицы, набора случайных и непонятных символов, не имеющих смысла. Поскольку сам процесс вбивания заведомо неправильных данных в пользовательский интерфейс ему кажется порой процессом бессмысленным, то он стал частенько использовать данное слово.
В качестве доказательства принимается скрин того, что вы найдете.