Практика 3 Побитовые операторы & Модулярная алгербра#

Битовое представление чисел#

Все целые числа можно записать в двоичной системе счисления:

$5_{10} = 101_2 = 4 + 1$

$42_{10} = 101010_2 = 32 + 8 + 2$

$256_{10} = 100000000_2 = 2^8$

Так как на уровне схем почти вся логика бинарная, именно такое представление и используется для хранения чисел в компьютерах: каждая целочисленная переменная указывает на какую-то ячейку из 8 (char), 16 (short), 32 (int) или 64 (long long) бит.

Порядок хранения битов в компьютерах#

Единственная неоднозначность в таком формате возникает с порядком хранения битов — также называемый порядок байт. В зависимости от архитектуры он может быть разным:

При схеме little-endian сначала идут младшие биты. Например, число $42_{10}$ будет храниться так:
010101010101.
При записи в формате big-endian сначала идут старшие биты. Все примеры из начала статьи даны в big-endian формате.

Хотя big-endian более естественен для понимания — на бумаге мы обычно и записываем бинарные числа — по разным причинам на большинстве современных процессоров по умолчанию используется little-endian.

Иными словами, « $i$ -ый бит» означает « $i$ -ый младший» или « $i$ -ый справа», но на бумаге мы ничего не инвертируем и записываем двоичные числа стандартным образом.

Основные побитовые операторы#

Помимо арифметических операций, с числами можно делать и битовые, которые интерпретируют их просто как последовательность битов.

Побитовые операторы играют важную роль в низкоуровневом программировании и манипуляции данными. Они позволяют выполнять операции на уровне отдельных битов, что может быть полезно для оптимизации производительности и работы с аппаратным обеспечением.

Cуществует несколько основных побитовых операторов:

Побитовое И (AND)- &: Этот оператор сравнивает каждый бит двух операндов и возвращает 1, если оба бита равны 1. В противном случае возвращает 0.
Побитовое ИЛИ (OR) - |: Этот оператор сравнивает каждый бит двух операндов и возвращает 1, если хотя бы один из битов равен 1. В противном случае возвращает 0.
Побитовое исключающее ИЛИ (XOR) - ^: Этот оператор сравнивает каждый бит двух операндов и возвращает 1, если один из битов равен 1, а другой - 0. Если оба бита одинаковы, возвращает 0.
Побитовое отрицание (NOT) - ~: Этот оператор инвертирует все биты операнда, превращая 1 в 0 и 0 в 1.
Побитовый сдвиг влево - «: Этот оператор сдвигает биты операнда влево на указанное количество позиций. Освободившиеся справа биты заполняются нулями.
Побитовый сдвиг вправо- »: Этот оператор сдвигает биты операнда вправо на указанное количество позиций. Освободившиеся слева биты заполняются нулями (или знаковыми битами в случае знакового типа).

Примеры использования побитовых операторов#

Побитовое И (AND)

PythonC++

    a = 5  # 0101
    b = 3  # 0011
    result = a & b  # какой будет результат?
    print(f"Побитовое И: {result}")

    unsigned int a = 5;  // 0101 в двоичном виде
    unsigned int b = 3;  // 0011 в двоичном виде
    unsigned int result = a & b;  // какой будет результат?

Побитовое ИЛИ (OR)

PythonC++

    a = 5  # 0101
    b = 3  # 0011
    result = a | b  # какой будет результат?
    print(f"Побитовое ИЛИ: {result}")

    unsigned int a = 5;  // 0101 в двоичном виде
    unsigned int b = 3;  // 0011 в двоичном виде
    unsigned int result = a | b;  // какой будет результат?

Побитовое исключающее ИЛИ (XOR)

PythonC++

    a = 5  # 0101
    b = 3  # 0011
    result = a ^ b  # какой будет результат?
    print(f"Побитовое XOR: {result}")

    unsigned int a = 5;  // 0101 в двоичном виде
    unsigned int b = 3;  // 0011 в двоичном виде
    unsigned int result = a ^ b;  // какой будет результат?

Побитовое отрицание (NOT)

PythonC++

    a = 5  # 0101
    b = 3  # 0011
    result = ~a  # какой будет результат?
    print(f"Побитовое NOT: {result}")

    unsigned int a = 5;  // 0101 в двоичном виде
    unsigned int result = ~a;   // какой будет результат?

Побитовый сдвиг влево

PythonC++

    a = 5  # 0101
    b = 3  # 0011
    result = a << 1  # какой будет результат?
    print(f"Побитовый сдвиг влево: {result}")

    unsigned int a = 5;  // 0101 в двоичном виде
    unsigned int result = a << 1;  // какой будет результат?

Побитовый сдвиг вправо

PythonC++

    a = 5  # 0101
    b = 3  # 0011
    result = a >> 1  # какой будет результат?
    print(f"Побитовый сдвиг вправо: {result}")

    unsigned int a = 5;  // 0101 в двоичном виде
    unsigned int result = a >> 1;  // какой будет результат?

Целочисленные переменные: знаковые и беззнаковые#

Целочисленные переменные делятся на два типа — знаковые (signed) и беззнаковые (unsigned).

Если сложить две unsigned int переменные, сумма которых превосходит $2^{32}$ , произойдет переполнение:
сумму нельзя будет представить точно, и поэтому вместо неё результатом будут только нижние 32 бита.
Все операции с беззнаковыми числами как бы проходят по модулю степени двойки.

Знаковые типы нужны для хранения значений, которые могут быть и отрицательными.
Для этого выделяется один бит для хранения знака (отрицательное ли число или нет),
из-за чего верхняя граница представимых чисел уменьшается:

Беззнаковые числа: максимальное значение — $2^{32} - 1$ .
Знаковые числа: максимальное значение — $2^{31} - 1$ .

Представление отрицательных чисел#

Разработчики процессоров стремятся к максимальному упрощению и экономии транзисторов.
Поэтому в signed типах переполнение происходит так же, как и у unsigned.

Чтобы сохранить свойства арифметики, отрицательное число $-x$ представляется как:

$-x = 2^{32} - x$

Следствия:
1. Все неотрицательные числа записываются так же, как и раньше.
2. У всех отрицательных чисел старший бит — единица.
3. Если прибавить к $2^{31} - 1$ единицу, то результатом будет $-2^{31}$ , который представляется как 10000000 (в целях изложения будем записывать 8 бит, хотя в int их 32).
4. Зная двоичную запись положительного числа x, запись -x можно получить как:

$-x = \sim x + 1$
5. -1 записывается как:

$\sim 1 + 1 = 11111110 + 00000001 = 11111111$
6. -42 записывается как:

$\sim 42 + 1 = 11010101 + 00000001 = 11010110$

После -1 = 11111111 идет 0:

$-1 + 1 = 11111111 + 00000001 = 00000000$

Что такое битовые флаги?#

Битовые флаги – это способ использования отдельных битов в переменной для хранения булевых значений. Вместо использования отдельных переменных типа bool, мы можем использовать один целочисленный тип данных, где каждый бит отвечает за одно булевое значение. Это помогает экономить память и упрощает управление множеством булевых переменных.

PythonC++

    # Определяем флаги
    FLAG_A = 1 << 0  # 0001
    FLAG_B = 1 << 1  # 0010
    FLAG_C = 1 << 2  # 0100

    flags = 0  # Изначально все флаги сброшены

    # Устанавливаем флаг A
    flags |= FLAG_A
    print(f"Флаг A установлен: {'Да' if (flags & FLAG_A) else 'Нет'}")

    # Устанавливаем флаг B
    flags |= FLAG_B
    print(f"Флаг B установлен: {'Да' if (flags & FLAG_B) else 'Нет'}")

    # Проверяем флаг C
    print(f"Флаг C установлен: {'Да' if (flags & FLAG_C) else 'Нет'}")

    # Сбрасываем флаг A
    flags &= ~FLAG_A
    print(f"Флаг A установлен: {'Да' if (flags & FLAG_A) else 'Нет'}")

    #include <iostream>

    const unsigned int FLAG_A = 1 << 0; // 0001
    const unsigned int FLAG_B = 1 << 1; // 0010
    const unsigned int FLAG_C = 1 << 2; // 0100

    int main() {
        unsigned int flags = 0;

        // Устанавливаем флаг A
        flags |= FLAG_A;
        std::cout << "Флаг A установлен: " << ((flags & FLAG_A) ? "Да" : "Нет") << std::endl;

        // Устанавливаем флаг B
        flags |= FLAG_B;
        std::cout << "Флаг B установлен: " << ((flags & FLAG_B) ? "Да" : "Нет") << std::endl;

        // Проверяем флаг C
        std::cout << "Флаг C установлен: " << ((flags & FLAG_C) ? "Да" : "Нет") << std::endl;

        // Сбрасываем флаг A
        flags &= ~FLAG_A;
        std::cout << "Флаг A установлен: " << ((flags & FLAG_A) ? "Да" : "Нет") << std::endl;

        return 0;
    }

Маски#

Бинарные последовательности можно поставить в соответствие подмножествам какого-то фиксированного множества: если на
𝑖-той позиции стоит единица, то значит 𝑖-тый элемент входит в множество, а иначе — не входит.

Битовые операции таким образом часто используются для работы с множествами, представляемыми битовыми масками — например, в задачах на полный перебор или динамическое программирование.

PythonC++

    # Определяем маску
    MASK = 0xF0  # 11110000

    # Исходное значение
    value = 0xAA  # 10101010

    # Применяем маску для выделения старших 4 битов
    masked_value = value & MASK
    print(f"Значение после применения маски: {hex(masked_value)}")

    #include <iostream>

    const unsigned int MASK = 0xF0; // 11110000

    int main() {
        unsigned int value = 0xAA; // 10101010

        // Применяем маску для выделения старших 4 битов
        unsigned int maskedValue = value & MASK;
        std::cout << "Значение после применения маски: " << std::hex << maskedValue << std::endl;

        return 0;
    }

Задание 1: Работа с битовыми флагами#

Создайте программу, которая использует битовые флаги для управления состояниями пользователя в системе. Определите следующие флаги:

Флаг администратора (ADMIN_FLAG)
Флаг активного пользователя (ACTIVE_FLAG)
Флаг премиум пользователя (PREMIUM_FLAG)

Пример работы программы:
Введите флаги для установки (через пробел, например: 1 2): 1 2
Администратор: Да
Активный пользователь: Да
Премиум пользователь: Нет

Сбрасываем флаг администратора
Администратор: Нет
Активный пользователь: Да
Премиум пользователь: Нет

Устанавливаем флаг премиум пользователя
Администратор: Нет
Активный пользователь: Да
Премиум пользователь: Да

PythonC++

    ADMIN_FLAG = 1 << 0    # 0001
    ACTIVE_FLAG = 1 << 1   # 0010
    PREMIUM_FLAG = 1 << 2  # 0100

    def set_flags(flags, values):
        for val in values:
             #  Продолжите код 
        return flags

    def clear_flag(flags, flag):
        return  #  Продолжите код 

    def check_flag(flags, flag):
        return "Да" if (flags & flag) else "Нет"


    flags = 0
    user_input = input("Введите флаги для установки (через пробел, например: 1 2): ").split()
    flag_map = {"1": ADMIN_FLAG, "2": ACTIVE_FLAG, "3": PREMIUM_FLAG}

    flags = set_flags(flags, [flag_map[val] for val in user_input if val in flag_map])
    #  Продолжите код

    #include <iostream>

    const unsigned int ADMIN_FLAG = 1 << 0;    // 0001
    const unsigned int ACTIVE_FLAG = 1 << 1;   // 0010
    const unsigned int PREMIUM_FLAG = 1 << 2;  // 0100

    unsigned int setFlag(unsigned int flags, unsigned int flag) {
        return // дополните
    }

    unsigned int clearFlag(unsigned int flags, unsigned int flag) {
        return // дополните
    }

    std::string checkFlag(unsigned int flags, unsigned int flag) {
        return (flags & flag) ? "Да" : "Нет";
    }

    int main() {
        unsigned int flags = 0;
        int choice;
        setlocale(LC_CTYPE, "rus");
        std::cout << "Введите флаги для установки (1 - Администратор, 2 - Активный, 3 - Премиум, 0 - завершить ввод):" << std::endl;

        while (true) {
            std::cin >> choice;
            if (choice == 0) break;
            if (choice == 1) flags = setFlag(flags, ADMIN_FLAG);
            if (choice == 2) flags = setFlag(flags, ACTIVE_FLAG);
            if (choice == 3) flags = setFlag(flags, PREMIUM_FLAG);
        }
       // Продолжите код 
    }

Модулярная алгербра#

Модулярная арифметика (арифметика по модулю) часто рассматривается как концептуальный уровень, который скрывает низкоуровневые битовые операции. Однако во многих случаях можно представить её именно как абстракцию над ними. Рассмотрим несколько примеров.

Модулем числа называют остаток от его деления на некоторое фиксированное число (основание модуля).

Обозначение:
$x \mod m$
означает остаток от деления $x$ на $m$ .

Например:
$17 \mod 5 = 2, \quad 29 \mod 8 = 5$

Note

В python и C++ реализован данный оператор как %.

PythonC++

    x1, m1 = 17, 5
    x2, m2 = 29, 8

    print(f"17 mod 5 = {x1 % m1}")
    print(f"29 mod 8 = {x2 % m2}")

    #include <iostream>

    int main() {
        int x1 = 17, m1 = 5;
        int x2 = 29, m2 = 8;

        std::cout << "17 mod 5 = " << (x1 % m1) << std::endl;
        std::cout << "29 mod 8 = " << (x2 % m2) << std::endl;

        return 0;
    }

Нахождение наибольшего общего делителя (НОД)#

Даны два натуральных числа. Требуется найти их наибольший общий делитель (НОД) — максимальное из натуральных чисел, которые делят их оба нацело.
Для чисел 12 и 18:
- Делители 12: 1, 2, 3, 4, 6, 12
- Делители 18: 1, 2, 3, 6, 9, 18
- НОД(12, 18) = 6, так как 6 — наибольшее число, которое делит оба числа.

В английском языке наибольший общий делитель называется greatest common divisor (gcd), это обозначение будет использоваться в формулах и программном коде.

Тривиальный алгоритм#

Легко можно реализовать решение «в лоб», которое будет перебирать все числа, начиная с единицы, и проверять каждое из них путем взятия остатка от обоих входных чисел. Такое решение — чрезвычайно простое, однако в то же время и весьма неэффективное.
Его время работы составит $O(n)$ , где $n$ — верхняя граница для входных чисел. Хотя это решение можно оптимизировать до некоторой степени (путем отсеивания заведомо ненужных чисел-кандидатов), далее мы рассмотрим принципиально другой алгоритм,
работающий гораздо быстрее при столь же простой реализации.

Алгоритм Евклида#

Алгоритм Евклида находит gcd двух чисел a и b за O(log min(a, b)),
основываясь на следующей несложной формуле:

$\gcd(a, b) = \begin{cases} a, & \text{если } b = 0 \\ \gcd(b,\, a - b), & \text{если } b > 0 \end{cases}$

Здесь предполагается, что $a > b$ .

Доказательство корректности
- Если $g = \gcd(a, b)$ делит и $a$ , и $b$ , то их разность $(a - b)$ тоже будет делиться на $g$ .
- Никакой больший делитель $d$ числа $b$ не может делить число $(a - b)$ : если $d > g$ , то $d$ не может делить $a$ , а значит и не делит $(a - b)$ .

Этот алгоритм может работать долго — например, на паре $(10^9, 1)$ он сделает миллиард итераций.

Идея дальнейшей оптимизации в том, чтобы вычитать из $a$ не одно $b$ за раз, а столько, чтобы в следующий раз $a$ и $b$ уже поменялись местами — чтобы новое $b$ стало меньше нового $a$ . Простой способ этого достичь — просто вычесть $b$ из $a$ сразу максимально возможное число раз, то есть взять вместо нового $b$ остаток от деления $a$ на $b$ :

$\gcd(a, b) = \begin{cases} a, & \text{если } b = 0 \\ \gcd(b,\, a \mod b), & \text{если } b > 0 \end{cases}$

Доказательство алгоритма более человеко-читаемое

Вначале докажем, что алгоритм Евклида всегда завершается. Для этого достаточно заметить, что второй аргумент на каждой итерации строго убывает — поэтому, учитывая, что он неотрицательный, число итераций алгоритма обязано быть конечным.

Теперь докажем корректность алгоритма, т. е. то, что величина в правой части определения действительно равна искомому НОД. Заметим, что для этого достаточно показать, что общие делители не меняются при переходе от пары (a, b) к паре (a - b, b), потому что операция взятия остатка эквивалентна операции вычитания, повторенной некоторое количество раз. Поскольку всякий общий делитель двух чисел также делит их сумму и их разность, то и утверждение про неизменность делителей при переходе между (a, b) и (a - b, b) тоже верно в обе стороны. Для завершения доказательства остается только рассмотреть случай \( b = 0 \); в этом случае \( a \) является правильным ответом, поскольку ноль делится на любое натуральное число.

Задание 2: Реализуйте (рекурсивной) функцией, используя блок-схему#

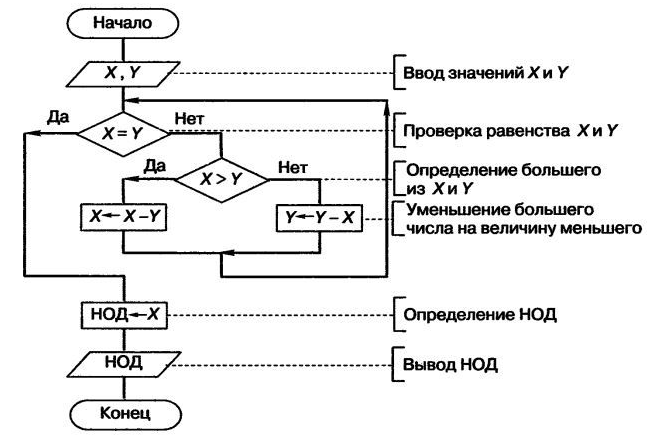
Фигура

Произведите оценку

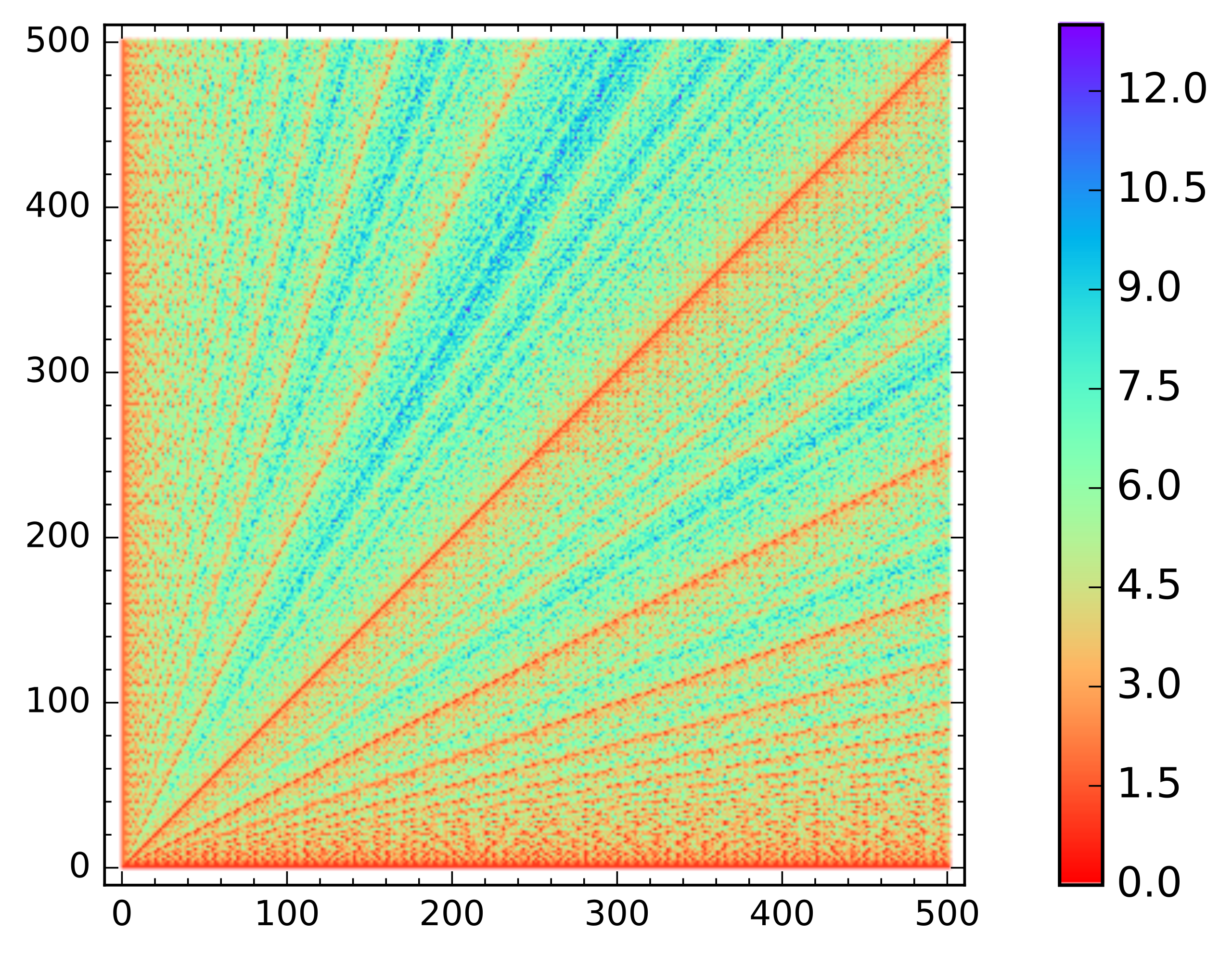
Фигура

Оценка Алгоритма Евклида

Можно показать, что каждые две итерации меньшее число уменьшится хотя бы в два раза, а следовательно алгоритм работает за

O(log(min(a, b))).

Эта оценка относится не только к худшему случаю, но и к среднему.

Примечательно, что худшие входные данные для алгоритма — это соседние числа Фибоначчи. На графике они видны как синие точки в пропорциях золотого сечения.

Также иногда полезно знать, что нахождение gcd группы из n чисел от 1 до A будет работать не за O(n log A), а за O(n + log A) — это несложно доказать по индукции.

Арфиметический бильярд#

Математический бильярд — это идеализированная модель обычного бильярда. В этой модели шар движется по тем же правилам, что и в реальном бильярде, но не обладает массой, а значит, отсутствует трение. Кроме того, на таком столе нет луз, поэтому шар будет отскакивать от бортов бесконечное количество раз и двигаться вечно.

Один из удивительных аспектов математического бильярда заключается в том, что он позволяет геометрически находить наименьшее общее кратное (НОК) и наибольший общий делитель (НОД) двух натуральных чисел.

Рассмотрите анимацию в GeoGebra (кнопка воспроизведения находится в нижнем левом углу) и попробуйте понять, как устроена эта конструкция. Чтобы запустить анимацию снова, дважды щёлкните на кнопку обновления в верхнем правом углу.

Для примера возьмём числа 40 и 15:
- НОК(40, 15) = 120
- НОД(40, 15) = 5

Базовая идея#

Рассмотрим два положительных целых числа $a$ и $b$ , ни одно из которых не является кратным другому (если одно является кратным другому, задача становится тривиальной и оставляется читателю).

Для бильярдного стола возьмём прямоугольник со сторонами длиной $a$ и $b$ . Запустим бильярдный шар из одного из углов (нижний левый на рисунке выше) под углом 45 градусов к сторонам. Шар отскакивает от стенок прямоугольника, не теряя скорости, и, согласно закону отражения, после каждого столкновения остаётся под углом 45 градусов к сторонам (то есть траектория шара состоит только из поворотов на 90 градусов влево или вправо).

Траектория движения шара представляет собой последовательность отрезков. Мы утверждаем, что в конечном итоге шар попадёт в один из углов. Кроме того, наименьшее общее кратное (НОК) чисел $a$ и $b$ равно длине пройденного пути от начальной точки до угла, делённой на $\gcd(a, b)$ .

Если разложить бильярдный стол на единичные квадраты (со стороной, равной единице), то НОК чисел $a$ и $b$ соответствует количеству единичных квадратов, которые пересекает траектория шара.

Также утверждается, что траектория шара пересекает саму себя. Первая часть траектории содержит точку самопересечения, которая расположена ближе всего к начальной точке. Наибольший общий делитель (НОД) чисел $a$ и $b$ равен расстоянию от начальной точки до этой ближайшей точки самопересечения, делённому на $\gcd(a, b)$ . Это также равно количеству единичных квадратов, через которые проходит траектория от начальной точки до первой точки самопересечения.

Зеркальное отражение#

Когда вы смотрите на объект в зеркале, создаётся впечатление, что он находится позади зеркала. Обратите внимание, что три точки лежат на одной прямой: ваша позиция, точка на зеркале, в которой виден объект, и (воображаемая) точка за зеркалом, где кажется, что объект находится. Чтобы доказать наши утверждения, мы воспользуемся этой простой идеей, рассматривая зеркало как одну из сторон бильярдного стола.

Наименьшее общее кратное (НОК) двух чисел $a$ и $b$ , обозначаемое как $\text{lcm}(a, b)$ , — это наименьшее натуральное число, которое делится и на $a$ , и на $b$ . Его можно представить в виде:

$\text{lcm}(a, b) = ka = mb$

для некоторых целых чисел $k$ и $m$ .

Если $a = 40$ и $b = 15$ , то:

$\text{lcm}(40, 15) = 120$

и его можно записать как:

$120 = 3 \times 40 = 8 \times 15.$

Рассмотрим два числа $a$ и $b$ , ни одно из которых не является кратным другому. Начнём с построения квадрата со сторонами длины $\text{lcm}(a, b)$ . Этот квадрат можно разложить на $k \times m$ прямоугольников со сторонами $a$ и $b$ .

Такое разбиение возможно, потому что:
- $a$ помещается в $\text{lcm}(a, b)$ ровно $k$ раз,
- $b$ помещается в $\text{lcm}(a, b)$ ровно $m$ раз.

Поскольку $\text{lcm}(a, b)$ является наименьшим общим кратным $a$ и $b$ , этот квадрат — наименьший, который можно полностью заполнить такими прямоугольниками.

Обозначим нижний левый угол квадрата как $A$ , а верхний правый — как $B$ . В дальнейшем эти точки помогут нам анализировать движение бильярдного шара и его отражения.

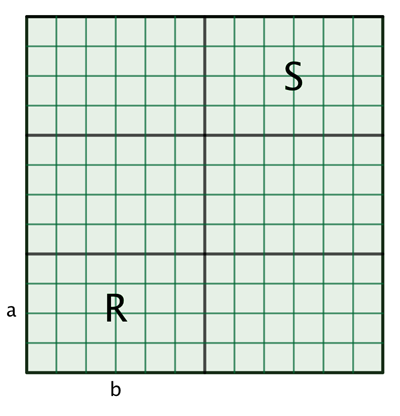
Фигура

Рассмотрим пример, где $a = 4$ и $b = 6$ . Их наименьшее общее кратное:

$\text{lcm}(4, 6) = 3 \times 4 = 2 \times 6 = 12.$

Таким образом, мы строим квадрат со сторонами длиной 12.

Этот квадрат можно разложить на $3 \times 2 = 6$ прямоугольников со сторонами $4$ и $6$ .

Теперь проведём диагональ d квадрата, начинающуюся в нижнем левом углу и заканчивающуюся в верхнем правом углу.

Эта диагональ пересечёт несколько внутренних границ прямоугольников, демонстрируя связь между разбиением квадрата и наибольшим общим делителем $\gcd(a, b)$ .

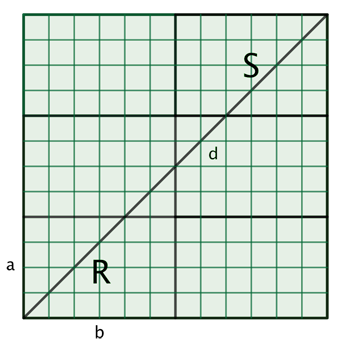
Фигура

Теперь из диагонали $d$ квадрата построим зигзагообразный путь $t$ , который полностью лежит в нижнем левом прямоугольнике $R$ . Этот путь формируется с помощью повторных отражений и в итоге совпадёт с траекторией движения бильярдного шара внутри прямоугольника.

Начнём с верхнего правого квадрата $S$ и отразим его относительно стороны, пересечённой диагональю $d$ . Эта сторона является общей границей с соседним прямоугольником $S$ (в данном случае — с прямоугольником ниже). Обозначим этот новый прямоугольник как $S'$ .

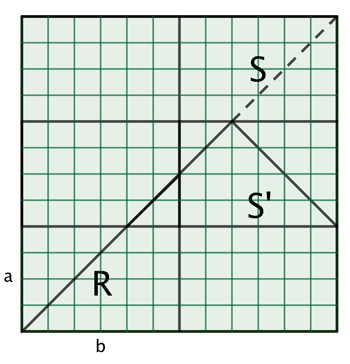
Фигура

Отражая квадрат $S$ относительно его нижней стороны, мы отражаем часть диагонали в прямоугольник ниже $S$ . Этот отражённый фрагмент диагонали будет частью пути, который будет следовать по траектории бильярдного шара, движущегося по прямоугольнику $S$ .

Теперь отразим прямоугольник $S'$ относительно другой стороны, пересекаемой диагональю $d$ (в нашем примере — это левая сторона). Это отражение не вернёт нас обратно в исходное положение, а вместо этого создаст новый прямоугольник, который продолжит путь зигзагообразного движения.

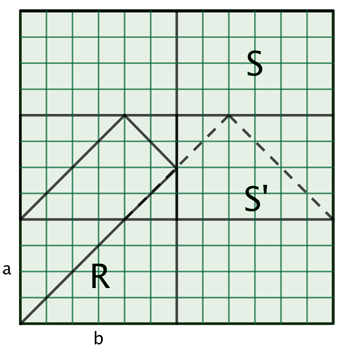
Фигура

Продолжим отражать прямоугольники по сторонам, пересекаемым диагональю $d$ , пока не дойдём до нижнего левого прямоугольника $R$ . Каждый раз, когда мы отражаем прямоугольник, мы продолжаем следовать по зигзагообразному пути, и эта траектория будет всё более точно имитировать путь бильярдного шара в пределах прямоугольника.

Повторные отражения превращают диагональ $d$ в зигзагообразный путь $t$ , который поочередно пересекает все прямоугольники, пока не вернётся в исходный прямоугольник $R$ . Этот процесс отражений позволяет нам создать путь, который полностью лежит внутри прямоугольника $R$ и будет повторяться бесконечно, если рассматривать его продолжение за пределы первоначального прямоугольника.

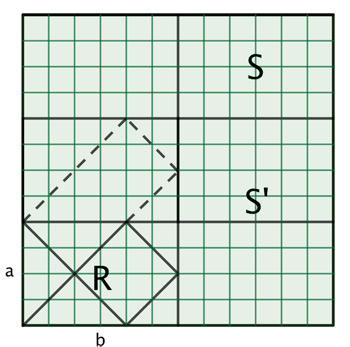
Фигура

Путь $t$ является точно тем же, что и траектория шара, выстреленного из нижнего левого угла прямоугольника $R$ под углом 45 градусов к его сторонам. Этот путь соответствует траектории бильярдного шара, который бесконечно отскакивает от стенок прямоугольника, не теряя скорости и отражаясь под углом 45 градусов.

Для того чтобы доказать, что путь $t$ действительно соответствует траектории шара, необходимо вспомнить, что шар будет совершать повороты на 90 градусов всякий раз, когда он столкнётся с боковой стороной прямоугольника $R$ .

Известно, что зигзагообразный путь $t$ , полученный через отражения, также будет следовать такому же правилу. Каждый раз, когда путь $t$ пересекает боковую сторону прямоугольника, он будет делать поворот на 90 градусов, что соответствует движению шара в бильярде.

Это проще всего объяснить с помощью картинки, где показано, как каждый сегмент траектории изменяет направление на 90 градусов при каждом отражении от стенки прямоугольника.

На картинке видно, что углы между сегментами пути составляют 90 градусов, что подтверждает, что это действительно путь, по которому движется бильярдный шар, отражаясь от стенок под углом 45 градусов.

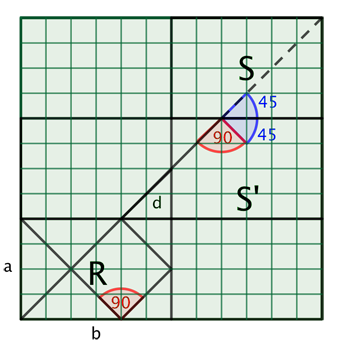
Фигура

Наш путь $t$ заканчивается в точке, которая получается из повторных отражений верхнего правого угла $S$ относительно сторон прямоугольников, поэтому конечная точка $t$ является углом прямоугольника $R$ .

Теперь длина пути $t$ равна длине диагонали $d$ . Длина диагонали любого квадрата равна $\sqrt{2}$ , умноженной на его сторону (это следует из теоремы Пифагора). Следовательно,

$|t| = \sqrt{2} \cdot \text{lcm}(a,b),$

где $|t|$ — это длина пути $t$ . Перемещая элементы, получаем,

$\text{lcm}(a,b) = \frac{|t|}{\sqrt{2}},$

что и требовалось доказать.

Наш метод прекрасно сработал в нашем примере, но можем ли мы быть уверены, что он работает для общих значений $a$ и $b$ (которые не являются кратными друг другу)? Единственное, что может пойти не так, — это если диагональ $d$ квадрата пересечёт угол прямоугольника, находящегося внутри квадрата. В этом случае мы не смогли бы определить, относительно какой из двух сторон, сходящихся в угле, проводить отражение.

Мы покажем, что это невозможно. Довольно легко убедиться, что любая точка $P$ на диагонали определяет квадрат: достаточно опустить вертикальную линию вниз до нижнего края исходного квадрата и провести горизонтальную линию влево до левого края исходного квадрата.

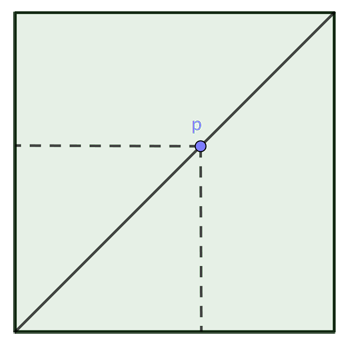
Фигура

Если бы такая точка также являлась углом одного из прямоугольников, то наш маленький квадрат был бы разложен на прямоугольники со сторонами $a$ и $b$ . Однако это невозможно: как мы отметили выше, квадрат со стороной $\text{lcm}(a, b)$ — наименьший квадрат, который можно разрезать таким образом.

Мы доказали, что $\text{lcm}(a, b)$ равен длине пути $t$ , делённой на $\sqrt{2}$ .

Перейдём теперь к единичным квадратам.

Единичные квадраты, пересекаемые траекторией#

Чтобы подсчитать количество единичных квадратов (квадратов со сторонами длины $1$ ), через которые проходит путь $t$ , мы снабжаем наш прямоугольник $R$ координатной системой. Вертикальная ось проходит вдоль левой стороны $R$ , а горизонтальная ось — вдоль нижней стороны $R$ . Координаты углов единичных квадратов являются целыми числами.

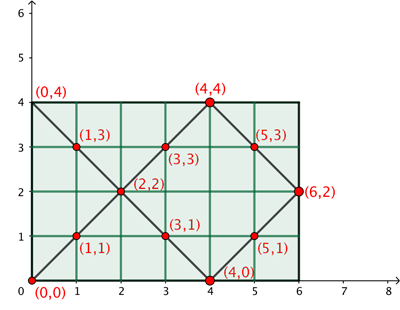
Фигура

Очевидно, что если $t$ пересекает единичный квадрат, то он делает это вдоль диагонали. Также можно убедиться, что если угол какого-либо единичного квадрата лежит на $t$ , то сумма его координат должна быть чётной. Каждый единичный квадрат имеет только две вершины, сумма координат которых чётна, и эти вершины расположены по диагонали друг к другу. Поэтому $t$ может проходить только вдоль одной из двух диагоналей единичного квадрата.

Мы оставляем вам задачу доказать, что $t$ никогда не проходит по диагонали одного и того же единичного квадрата дважды — ни в одном направлении, ни в обратном. Для этого необходимо показать, что конечная точка $t$ отличается от начальной. Обратите внимание, что хотя бы одно из чисел $m$ или $n$ должно быть нечётным, и конечная точка $t$ получается в результате многократного отражения верхнего правого угла прямоугольника $S$ .

Теперь мы знаем, что $t$ никогда не пересекает один и тот же единичный квадрат более одного раза и всегда делает это вдоль диагонали. Поскольку диагональ единичного квадрата имеет длину $\sqrt{2}$ , число квадратов, через которые проходит $t$ , равно

$\frac{|t|}{\sqrt{2}} = \frac{\sqrt{2}\, \text{lcm}(a,b)}{\sqrt{2}} = \text{lcm}(a,b),$

как и утверждалось ранее.

Наибольший общий делитель#

Мы утверждали, что наибольший общий делитель $\gcd(a,b)$ равен расстоянию от начальной точки $t$ до ближайшей точки самопересечения, делённому на $\sqrt{2}$ . Он также равен количеству единичных квадратов, через которые проходит отрезок пути от начальной точки до первой точки самопересечения.

Предположим сначала, что $\gcd(a,b)=1$ . В этом случае наименьшее общее кратное $a$ и $b$ равно их произведению $ab$ (попробуйте доказать это самостоятельно). По нашему предыдущему результату, количество единичных квадратов, пересечённых путём $t$ , также равно $ab$ .

Так как стороны прямоугольника $R$ имеют длины $a$ и $b$ , то всего в $R$ находится $ab$ единичных квадратов. А поскольку путь $t$ не пересекает ни один единичный квадрат более одного раза, он должен пройти через все $ab$ единичных квадратов в этом случае.

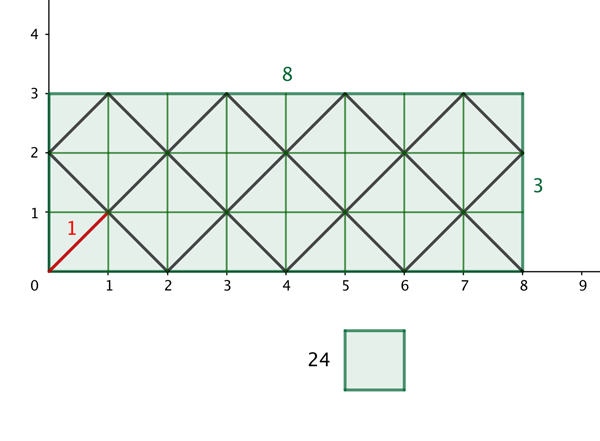
Фигура

Мы уже знаем, что углы единичных квадратов, лежащих на $t$ , имеют координаты, сумма которых является чётным числом. И наоборот, тот факт, что $t$ пересекает каждый единичный квадрат, означает, что любая точка с координатами, сумма которых чётна, лежит на $t$ .

Это означает, что точки с координатами $(0,0)$ , $(2,0)$ , $(0,2)$ и $(2,2)$ все лежат на $t$ . Такое возможно только в том случае, если точка $(1,1)$ является точкой самопересечения $t$ .

Таким образом, точка $(1,1)$ является точкой самопересечения $t$ и расположена на минимальном расстоянии от $(0,0)$ вдоль $t$ . Расстояние от $(0,0)$ до $(1,1)$ вдоль $t$ равно $\sqrt{2}$ . Разделив это расстояние на $\sqrt{2}$ , получаем $1$ — наибольший общий делитель $a$ и $b$ (по нашему предположению). Количество единичных квадратов, через которые проходит путь от $(0,0)$ до $(1,1)$ вдоль $t$ , также равно $1$ . Это доказывает наше первоначальное утверждение относительно $\gcd(a,b)$ для случая, когда $\gcd(a,b)=1$ .

Если $\gcd(a,b) \neq 1$ , то мы можем масштабировать всю фигуру с коэффициентом $\gcd(a,b)$ : разделив $a$ и $b$ на их наибольший общий делитель, получим два положительных числа, наибольший общий делитель которых равен $1$ . Затем можно повторить описанную выше конструкцию для этих чисел, а затем увеличить масштаб, умножив каждую ось нашей системы координат на $\gcd(a,b)$ . В этом случае единичные квадраты превращаются в квадраты со стороной $\gcd(a,b)$ . Все геометрические свойства, не связанные с длиной (форма пути, в какой угол попадает бильярдный шар и т.д.), остаются неизменными при таком масштабировании.

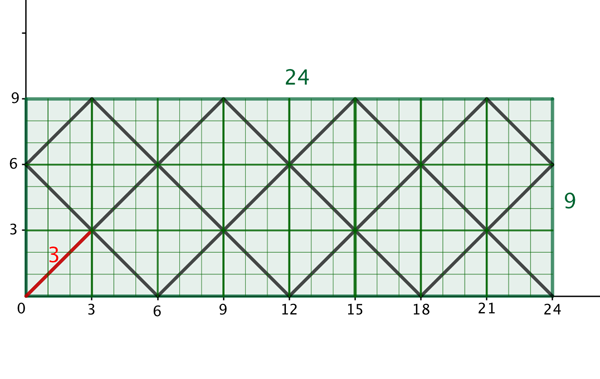
Фигура

Из этого следует, что точка самопересечения, расположенная ближе всего к начальной точке, лежит на первом отрезке пути на расстоянии $\sqrt{2} \cdot \gcd(a, b)$ от начального угла, и что $\gcd(a, b)$ — это количество единичных квадратов, пересечённых первым отрезком пути от начальной точки до ближайшей точки самопересечения.

Вопросы для закрепления

1. Если одно из двух заданных чисел кратно другому, какова форма арифметической траектории биллиарда? 
2. Для каких чисел арифметическая траектория биллиарда заканчивается в углу, противоположном начальной точке? 
3. Каковы симметрии арифметической бильярдной траектории (как геометрической фигуры)?

Примечание для желающих продолжить

Фигура

Братец кролик так долго готовил материалы к занятию, что катастрофически устал и не заметил, что пропустил номер у одной из картинок. (Каждая иллюстрация имеет свой номер, однако после иллюстрации N идет номер не N +1, а N+1. Для примера: после 7.png идет 9.,png)
Чтобы занять чем-то пропавший номер он разметил на осовбодившемся домене файл N.html, где N - пропавший номер.
Ваша задача найти и открыть неизвестную страницу и объяснить, почему вы её не видите в поисковике, но можете её открыть. Также предоставьте доказательства, что вы её нашли.