Практика 2 Как люди придумывают алгоритмы?#
Алгоритмы лежат в основе всех вычислительных процессов и являются неотъемлемой частью решения многих задач в программировании. На практике разработка алгоритма требует не только теоретических знаний, но и творческого подхода, способности искать оптимальные пути решения. Алгоритмы могут быть различными по сложности и области применения, однако все они стремятся к одной цели — эффективному решению проблемы.
Во время этой практики мы будем исследовать, как люди подходят к созданию алгоритмов, с какими трудностями сталкиваются при их разработке, и какие методы помогают найти решение. Мы изучим основные шаги создания алгоритмов, включая формулировку проблемы, выбор подходящих данных и структур, а также методы оптимизации.
Разминка#
Наше восприятие задачи сильно зависит от того, встречались ли мы раньше с чем-то похожим или нет. Зачастую мы склонны выбирать наиболее понятной интуитивное решение. Например, на прошлой практике мы говорили об оценке алгоритмов. Итуитивно многие сразу сказали, что основным критерием оценки будет время. Однако, как выяснилось, алгоритмы можно оценить по использованной памяти.
Что кроме времени выполнения и ресурсов компьютера может быть также важно? Ответ, казалось бы очевиден и в тоже время невероятен - точность алгоритма является не менее интересным критерием качества в реальной жизни.
Однако как может быть "неточным" точное устройство?
Во-первых, мы уже знаем, что точное устройство может быть неточным из-за наличия погрешностей в его работе, иначе говоря сбоях. Однако такой пример является аппаратной проблемой.
Во-вторых, для целей вычислений мы можем намеренно создавать такой алгоритм, который округляет, огрубляет значения. Причин тому великое множетсво : от невозможности решить задачу точно до проблем, связанных со временем необходимых вычислений.
Давайте рассмотрим классичекие алгоритмы вычисления Площадей фигур.
Площадь тривиальных фигур#
Постановка задачи
Пусть дан квадрат со сторонами а и b. Необходимо вычислить площадь. Ввод параметров с клавиатуры.
Хотя постановка задачи проста, вспомним некоторые важные команды: input для Python и cin для С++, которые обеспечивают чтение данных с клавиатуры.
# Ввод параметров
a = float(input("Введите длину стороны a: "))
# Вычисление площади
area = a * a
# Вывод результата
print(f"Площадь квадрата: {area}")
#include <iostream>
using namespace std;
int main() {
double a, b;
// Ввод параметров
cout << "Введите длину стороны a: ";
cin >> a;
// Вычисление площади
double area = a * a;
// Вывод результата
cout << "Площадь квадрата: " << area << endl;
return 0;
}
Можно привести еще некоторое количество подобных задач на вычисление площади: Трапеции, Треугольника, Окружности и проч.
Однако представим себе, что наша задача усложнилась.
Постановка задачи
Пусть дан квадрат, описанный точками. Необходимо вычислить площадь квадрата. Ввод параметров с клавиатуры.
Что изменилось для нас в постановке задачи? Изменились входные данные и теперь мы, как разработчики, должны понять, как вычислить расстояние между точками.
Не правда ли, что это потребует от нас некоторых знаний в области геометрии. Как программисты давай всопмним операцию возведения в степень и извлечение корня.
# Ввод координат точек квадрата
x1 = float(input("Введите координату x1: "))
y1 = float(input("Введите координату y1: "))
x2 = float(input("Введите координату x2: "))
y2 = float(input("Введите координату y2: "))
# Вычисление длины стороны квадрата через расстояние между двумя точками
side_length = # ваше предположение
# Вычисление площади
area = side_length ** 2
# Вывод результата
print(f"Площадь квадрата: {area}")
#include <iostream>
#include <cmath>
using namespace std;
int main() {
double x1, y1, x2, y2;
// Ввод координат точек
cout << "Введите координату x1: ";
cin >> x1;
cout << "Введите координату y1: ";
cin >> y1;
cout << "Введите координату x2: ";
cin >> x2;
cout << "Введите координату y2: ";
cin >> y2;
// Вычисление длины стороны квадрата через расстояние между двумя точками
double side_length = // ваше предположение
// Вычисление площади
double area = pow(side_length, 2);
// Вывод результата
cout << "Площадь квадрата: " << area << endl;
return 0;
}
Площадь криволинейных фигур#
Зададимся вопросо : часто ли мы встречаем в природе идеальный квадрат?
Обычно живые существа, да и прочие предметы вокруг нас, далеки от простых форм.
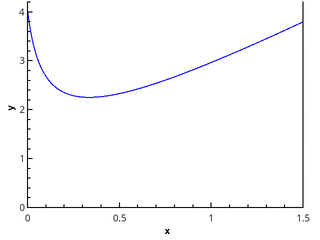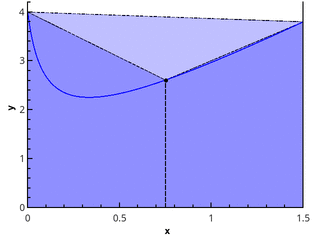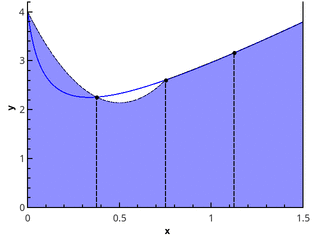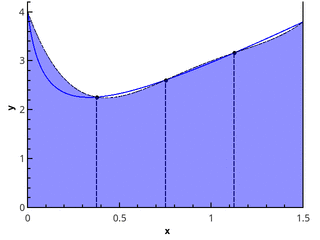
И допустим, есть у меня ужасная нужда посчитаь площадь амебы. Кстати, вот и она
Если долго смотреть на амебу, то можно заметить, что её плавные контуры жутко напоминают непрерывную функцию
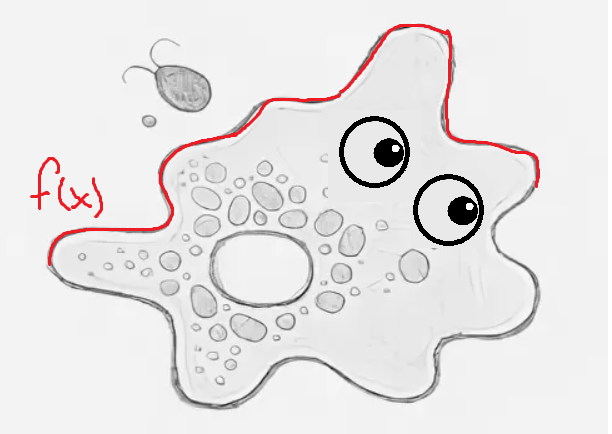
Тогда, возможно, стоит попытаться описать компьютеру такую функцию и указать, что необхожимо посчитать площадь прямо под этой кривой.
Проблема заключается в том, что компьютер не воспринимает не дискретные величины и поэтому нам нужно разбить нашу фигуру на фрагменты.
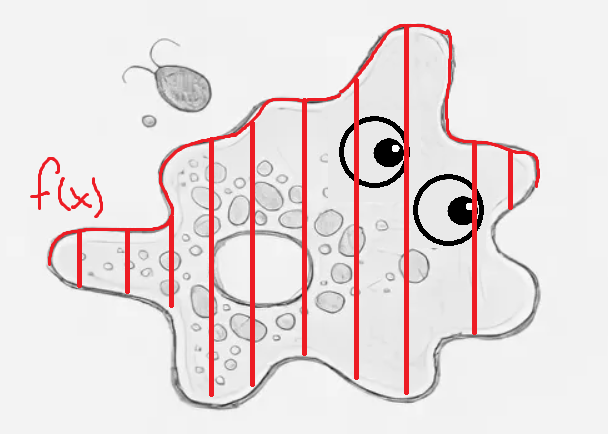
Вскоре можно заметить, что фрагменты похожи на прямоугольники, которые мы так ловко считали на разминке. Конечно, они всегда ровно совпадают с линией, особенно, если разбиение с малым числом шагов. Однако чем мельче я бужут мои линии, тем точнее у меня получится нарисовать прямоугольники, а сложим площади фигур мы получим примерную площадь амебы.
Идея целочисленного интегрирования#
Численное интегрирование (историческое название: (численная) квадратура) — вычисление значения определённого интеграла (как правило, приближённое). Под численным интегрированием понимают набор численных методов для нахождения значения определённого интеграла.
Численное интегрирование применяется, когда:
- Сама подынтегральная функция не задана аналитически. Например, она представлена в виде таблицы (массива) значений в узлах некоторой расчётной сетки.
- Аналитическое представление подынтегральной функции известно, но её первообразная не выражается через аналитические функции. Например, f(x) = \exp(-x^2) .
В этих двух случаях невозможно вычисление интеграла по формуле Ньютона — Лейбница. Также возможна ситуация, когда вид первообразной настолько сложен, что быстрее вычислить значение интеграла численным методом.
Основная идея большинства методов численного интегрирования состоит в замене подынтегральной функции на более простую, интеграл от которой легко вычисляется аналитически. При этом для оценки значения интеграла получаются формулы вида:
где n — число точек, в которых вычисляется значение подынтегральной функции. Точки x_i называются узлами метода, числа w_i — весами узлов.
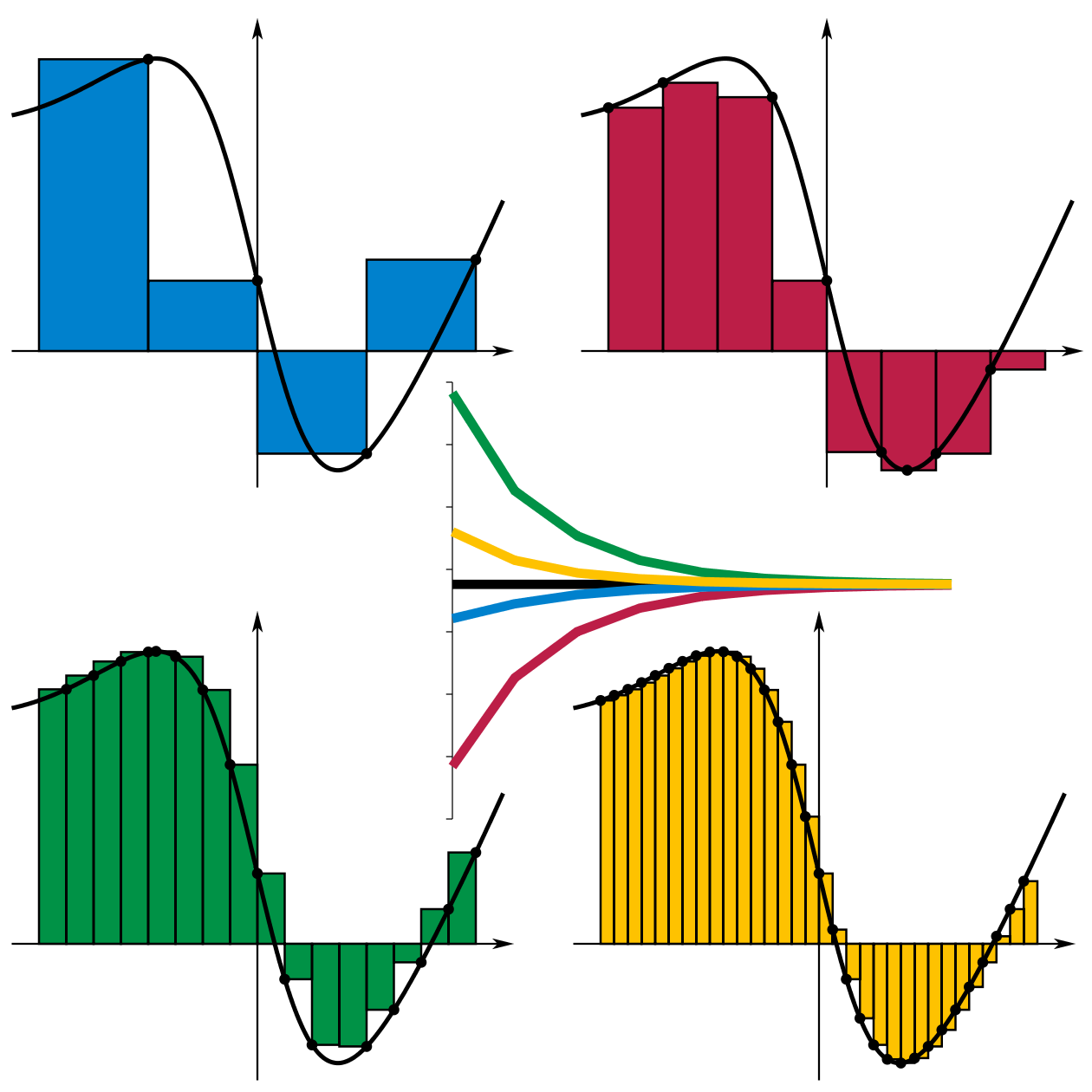
При замене подынтегральной функции на полином нулевой, первой и второй степени получаются соответственно методы прямоугольников, трапеций и парабол (Симпсона). Часто формулы для оценки значения интеграла называют квадратурными формулами.
Метод прямоугольников#
Метод прямоугольников является одним из самых простых методов численного интегрирования. Суть метода заключается в том, чтобы заменить область под графиком функции прямоугольниками, площадь которых легко вычисляется.
Для нахождения значения интеграла с помощью метода прямоугольников, подынтегральная функция f(x) аппроксимируется прямыми отрезками, соединяющими точки функции на определённых интервалах.
Квадратурная формула метода прямоугольников выглядит следующим образом:
где:
- n — количество узлов (точек),
- x_i — значения точек, в которых вычисляется функция,
- w_i — веса узлов, обычно для метода прямоугольников w_i = \Delta x , где \Delta x — шаг между узлами.
Часто метод прямоугольников применяется на равномерно расположенных точках, и шаг \Delta x вычисляется как:
где a и b — границы интегрирования, а n — количество интервалов.
# Метод прямоугольников для численного интегрирования
def rectangle_method(f, a, b, n):
# Вычисляем шаг
delta_x = (b - a) / n
# Суммируем значения функции в узловых точках
integral = 0
for i in range(n):
x_i = a + i * delta_x # Левая точка интервала
integral += f(x_i)
# Умножаем на шаг
integral *= delta_x
return integral
# Пример использования: интегрирование функции exp(-x^2) на интервале [0, 1]
import math
def func(x):
return math.exp(-x**2)
a = 0 # Начало интервала
b = 1 # Конец интервала
n = 1000 # Количество интервалов
result = rectangle_method(func, a, b, n)
print(f"Численное значение интеграла: {result}")
#include <iostream>
#include <cmath>
using namespace std;
// Метод прямоугольников для численного интегрирования
double rectangle_method(double (*f)(double), double a, double b, int n) {
// Вычисляем шаг
double delta_x = (b - a) / n;
// Суммируем значения функции в узловых точках
double integral = 0;
for (int i = 0; i < n; i++) {
double x_i = a + i * delta_x; // Левая точка интервала
integral += f(x_i);
}
// Умножаем на шаг
integral *= delta_x;
return integral;
}
// Пример использования: интегрирование функции exp(-x^2) на интервале [0, 1]
double func(double x) {
return exp(-x * x);
}
int main() {
double a = 0; // Начало интервала
double b = 1; // Конец интервала
int n = 1000; // Количество интервалов
double result = rectangle_method(func, a, b, n);
cout << "Численное значение интеграла: " << result << endl;
return 0;
}
Формула Симпсона#
Формула Симпсона является более точным методом численного интегрирования по сравнению с методами прямоугольников и трапеций. Метод Симпсона использует аппроксимацию подынтегральной функции полиномом второй степени (параболой), что позволяет значительно улучшить точность вычислений.
Формула Симпсона используется для вычисления интегралов на интервале [a, b], разбитом на чётное количество подынтервалов. Для расчёта интеграла на одном интервале формула имеет вид:
где:
- \Delta x = \frac{b - a}{2} — шаг между узлами (с учетом, что количество разбиений чётное),
- f(a) , f(b) , и f\left( \frac{a+b}{2} \right) — значения функции в точках на концах интервала и в середине.
Для вычисления интеграла на большем интервале с использованием нескольких подинтервалов, используется обобщённая формула Симпсона:
где:
- x_0 = a , x_n = b — концы интервала,
- x_i — узлы метода, которые расположены через шаг \Delta x .
Таким образом, метод Симпсона требует, чтобы количество подинтервалов было чётным, и использует более точную аппроксимацию функции, чем методы прямоугольников и трапеций.
# Метод Симпсона для численного интегрирования
def simpson_method(f, a, b, n):
# Проверяем, что n чётное
if n % 2 == 1:
n += 1
# Вычисляем шаг
delta_x = (b - a) / n
# Вычисление значений функции в узловых точках
integral = f(a) + f(b)
# Суммируем для нечётных и чётных индексов
for i in range(1, n, 2):
integral += 4 * f(a + i * delta_x)
for i in range(2, n-1, 2):
integral += 2 * f(a + i * delta_x)
# Умножаем на шаг / 3
integral *= delta_x / 3
return integral
# Пример использования: интегрирование функции exp(-x^2) на интервале [0, 1]
import math
def func(x):
return math.exp(-x**2)
a = 0 # Начало интервала
b = 1 # Конец интервала
n = 1000 # Количество разбиений (должно быть чётным)
result = simpson_method(func, a, b, n)
print(f"Численное значение интеграла: {result}")
#include <iostream>
#include <cmath>
using namespace std;
// Метод Симпсона для численного интегрирования
double simpson_method(double (*f)(double), double a, double b, int n) {
// Проверяем, что n чётное
if (n % 2 == 1) {
n += 1; // Увеличиваем n, если оно нечётное
}
// Вычисляем шаг
double delta_x = (b - a) / n;
// Вычисление значений функции в узловых точках
double integral = f(a) + f(b);
// Суммируем для нечётных и чётных индексов
for (int i = 1; i < n; i += 2) {
integral += 4 * f(a + i * delta_x);
}
for (int i = 2; i < n - 1; i += 2) {
integral += 2 * f(a + i * delta_x);
}
// Умножаем на шаг / 3
integral *= delta_x / 3;
return integral;
}
// Пример использования: интегрирование функции exp(-x^2) на интервале [0, 1]
double func(double x) {
return exp(-x * x);
}
int main() {
double a = 0; // Начало интервала
double b = 1; // Конец интервала
int n = 1000; // Количество разбиений (должно быть чётным)
double result = simpson_method(func, a, b, n);
cout << "Численное значение интеграла: " << result << endl;
return 0;
}
Прогрессирующая сложность#
Вычисление площади фигур в реальности может быть сложным из-за необходимости точного описания формы объекта. Для того чтобы вычислить площадь, его форма должна быть представлена математически, однако многие реальные объекты и фигуры не имеют простых аналитических выражений и могут быть либо нерегулярными, либо слишком сложными для точного математического представления. В некоторых случаях геометрия объектов оказывается слишком сложной для традиционных аналитических методов. Например, фигуры могут иметь изломанные, фрактальные или многогранные формы, которые трудно выразить с помощью простых формул или вычислить с использованием классических методов.
Метод Монте-Карло#
Метод Монте-Карло может быть применен для поиска площади произвольной геометрической фигуры. Пусть геометрическая фигура A находится внутри прямоугольника с размерами W \times H , и требуется найти площадь фигуры S_A .
Сгенерируем случайную точку (x, y) внутри прямоугольника равномерным образом. Тогда согласно геометрическому определению вероятности, вероятность того, что эта точка окажется внутри геометрической фигуры A , определяется соотношением:
где S_{\text{rectangle}} — площадь прямоугольника. Таким образом, чтобы найти S_A , достаточно знать вероятность P .
Применение метода Монте-Карло заключается в том, чтобы оценить эту самую вероятность эмпирически. Для этого генерируется N случайных точек внутри прямоугольника, подсчитывается количество точек N_{\text{inside}} , оказавшихся внутри фигуры A , и принимается, что если N достаточно велико, то:
Этот метод работает с любыми сложными геометрическими фигурами, где аналитические способы нахождения площади трудны или невозможны.
Tip
Генерировать выборку случайных чисел, равномерно распределенных на отрезке [low, high] можно методом numpy.random.uniform.
import random
import math
# Функция для вычисления площади круга методом Монте-Карло
def monte_carlo_circle_area(R, num_points):
points_inside = 0
for _ in range(num_points):
# Генерируем случайную точку в квадрате с центром в (0, 0) и стороной 2R
x = random.uniform(-R, R)
y = random.uniform(-R, R)
# Проверяем, попала ли точка внутри круга
if x**2 + y**2 <= R**2:
points_inside += 1
# Площадь квадрата
square_area = (2 * R) ** 2
# Приближенная площадь круга
circle_area = (points_inside / num_points) * square_area
return circle_area
# Пример использования
R = 1 # Радиус круга
num_points = 1000000 # Количество случайных точек
result = monte_carlo_circle_area(R, num_points)
print(f"Приближенная площадь круга: {result}")
#include <iostream>
#include <cstdlib>
#include <ctime>
#include <cmath>
using namespace std;
// Функция для вычисления площади круга методом Монте-Карло
double monte_carlo_circle_area(double R, int num_points) {
int points_inside = 0;
for (int i = 0; i < num_points; ++i) {
// Генерируем случайную точку в квадрате с центром в (0, 0) и стороной 2R
double x = (rand() / (RAND_MAX + 1.0)) * 2 * R - R; // Случайное число в диапазоне [-R, R]
double y = (rand() / (RAND_MAX + 1.0)) * 2 * R - R; // Случайное число в диапазоне [-R, R]
// Проверяем, попала ли точка внутри круга
if (x * x + y * y <= R * R) {
points_inside++;
}
}
// Площадь квадрата
double square_area = (2 * R) * (2 * R);
// Приближенная площадь круга
return (points_inside / static_cast<double>(num_points)) * square_area;
}
int main() {
srand(time(0)); // Инициализируем генератор случайных чисел
double R = 1; // Радиус круга
int num_points = 1000000; // Количество случайных точек
double result = monte_carlo_circle_area(R, num_points);
cout << "Приближенная площадь круга: " << result << endl;
return 0;
}
Если у нас есть формальное требование точности ответа — например, получение 3 правильных значимых знаков хотя бы в 99% случаев — возникает вопрос, сколько точек необходимо проверить.
Можно показать, что для получения k правильных значимых знаков с вероятностью, произвольно близкой к единице, необходимо:
где n — количество проверяемых точек.
Это означает, что при увеличении требуемого числа правильных знаков k число необходимых точек растёт экспоненциально. Например:
- Для k = 3 значимых знаков потребуется n = \Theta(10^6) точек.
- Для k = 4 значимых знаков уже n = \Theta(10^8) точек.
Данный факт выводится из теории оценок (теория вероятность)
