Перейти к содержанию

ДЗ Лабораторная работа №2 "Расчет площади фигуры"#

Warning

За задание можно получить до 5 баллов, соблюдая следующие условия:
- Написано на C++ ( + 1 балл)
- Тестрование проводилось с использованием Unit-test ( + 1 балл)
- Задание зачтено ( +3 балла)

В отчете должно быть указано следующие:
1. Титульный лист, где указаны ФИО преподавателя, номер задания, номер варианта
2. Формулировка задания (картинка и уравнения)
3. Ссылка на github-репозиторий с работающим кодом
4. Реализуйте Монте-Карло или Формулу Симпосона (в зависимости от варианта та или иная реализация будет удобнее) для расчета площади фигуры.
5. Вычислите расчетное значение площади криволинейной фигуры, используя интеграллы. Расчеты приведите. (Если вы не умеете еще рассчитывать, воспользуйтесь калькулятором, вбив уравнения)
5. Проведите эксперимент с расчетом площади фигуры при разном числе N. Дайте таблицу испытаний/разбиений.
6. На основе полученных данных ответьте на вопрос при каком N дальше не имеет смысла увеличивать число испытаний/разбиений?
7. Насколько точно вы смогли в ходе испытаний приблизиться к действительному значению?

Примечание: Для реализации Unit-test необходимо использовать assertAlmostEqual (assertAlmostEqual(a, b, places=7)) для Python (Проверяет, что a и b равны с точностью до places десятичных знаков) для 3 раных значений n. Для C++ для проверки приближённого равенства есть**AreEqual** с параметром точности (tolerance). Пример: Assert::AreEqual(a, b, epsilon, L"Значения совпали с точностью.");

Пример расчета интегралла криволинейной фигуры#

Необходимо определить площадь фигуры, которая ограничена параболой

и прямыми линиями

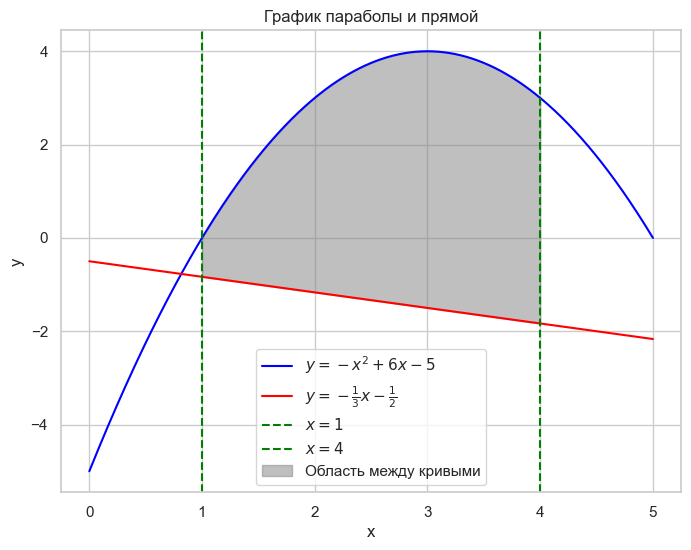
Фигура

Изобразим линии на графике в декартовой системе координат.

На отрезке [1; 4] график параболы y = -x^2 + 6x - 5 расположен выше прямой y = -\frac{1}{3}x - \frac{1}{2}. В связи с этим, для получения ответа используем формулу, полученную ранее, а также способ вычисления определенного интеграла по формуле Ньютона-Лейбница:

S(G) = \int_1^4 \left( -x^2 + 6x - 5 - \left( -\frac{1}{3}x - \frac{1}{2} \right) \right) dx
= \int_1^4 \left( -x^2 + \frac{19}{3}x - \frac{9}{2} \right) dx

Вычисляем определенный интеграл:

\left( -\frac{1}{3}x^3 + \frac{19}{6}x^2 - \frac{9}{2}x \right) \Big|_1^4

Подставляем пределы интегрирования:

= \left( -\frac{1}{3} \cdot 4^3 + \frac{19}{6} \cdot 4^2 - \frac{9}{2} \cdot 4 \right) - \left( -\frac{1}{3} \cdot 1^3 + \frac{19}{6} \cdot 1^2 - \frac{9}{2} \cdot 1 \right)
= \left( -\frac{64}{3} + \frac{152}{3} - 18 \right) - \left( -\frac{1}{3} + \frac{19}{6} - \frac{9}{2} \right)

Упрощаем:

= \frac{152}{3} - \frac{64}{3} - 18 + \frac{1}{3} - \frac{19}{6} + \frac{9}{2}

Ответ:

S(G) = 13

Метод Монте-Карло для вычисления площади фигуры#

Метод Монте-Карло — это статистический метод, использующий случайные числа для решения математических задач. Для вычисления площади фигуры можно применить этот метод следующим образом:

  1. Определение области для поиска: Укажите прямоугольную область, в которой будет заключена ваша фигура. Например, если фигура — это круг, то область может быть квадратом, в который вписан этот круг.

  2. Генерация случайных точек: Генерируйте случайные точки внутри указанной области.

  3. Проверка попадания в фигуру: Для каждой случайной точки проверяйте, попадает ли она в фигуру. Для круга, например, можно проверить, выполняется ли условие x^2 + y^2 \leq r^2, где r — радиус круга, а x и y — координаты точки.

  4. Расчет площади:

    • Общее количество случайных точек, попавших в фигуру, делится на общее количество сгенерированных точек.
    • Площадь фигуры будет пропорциональна площади всей области, умноженной на этот коэффициент:

  5. Увеличение точности: Чем больше точек будет сгенерировано, тем точнее будет результат.

Пример Вычисление площади круга

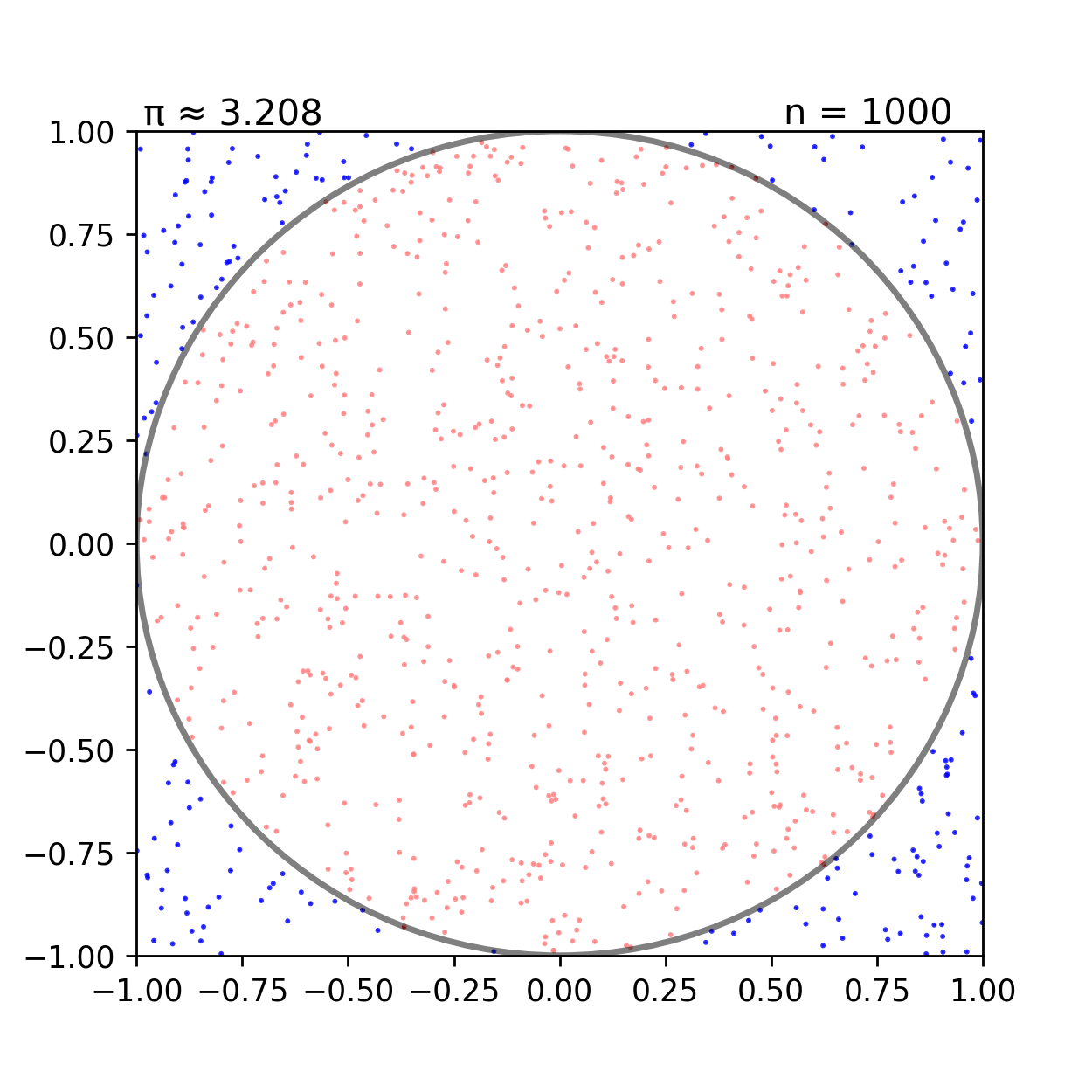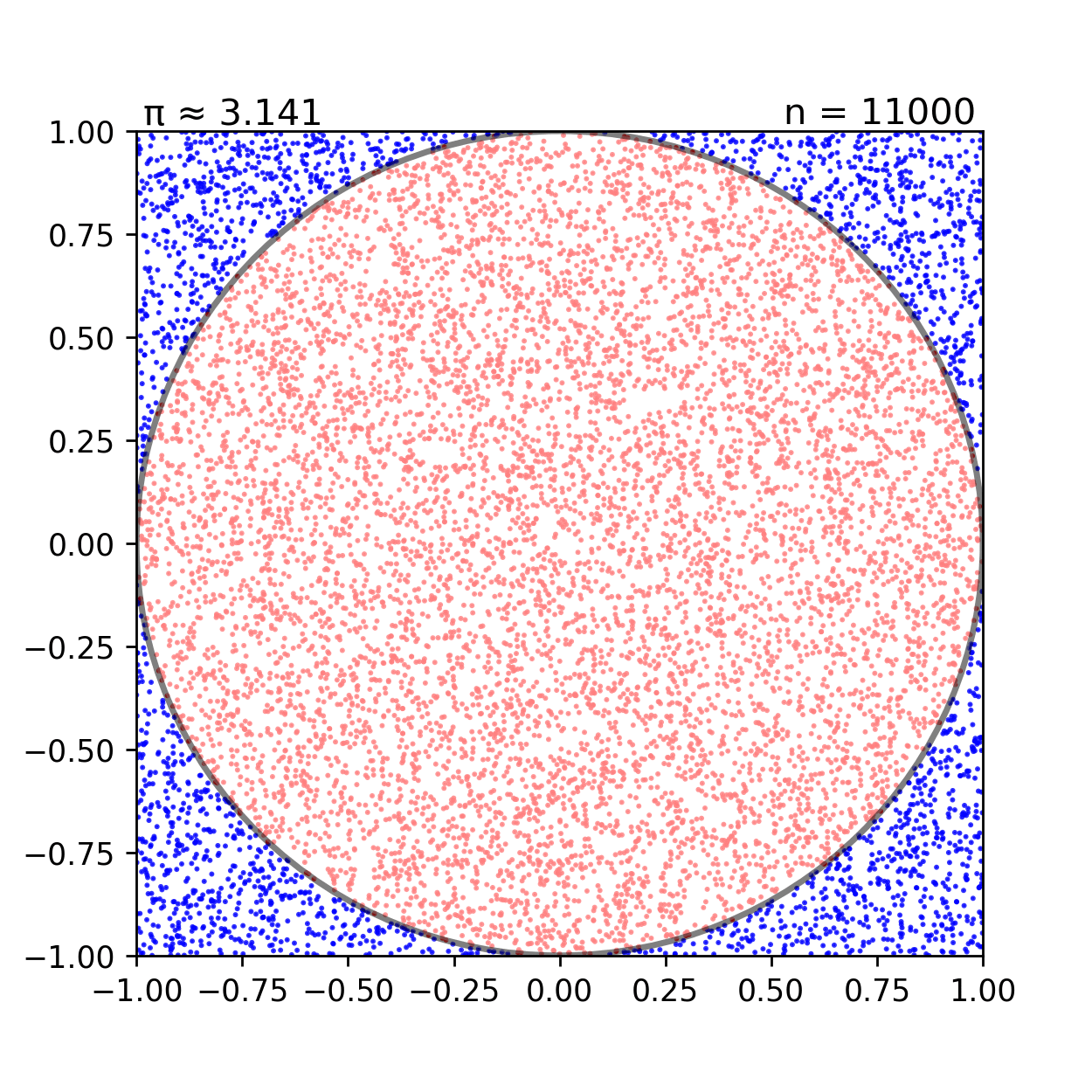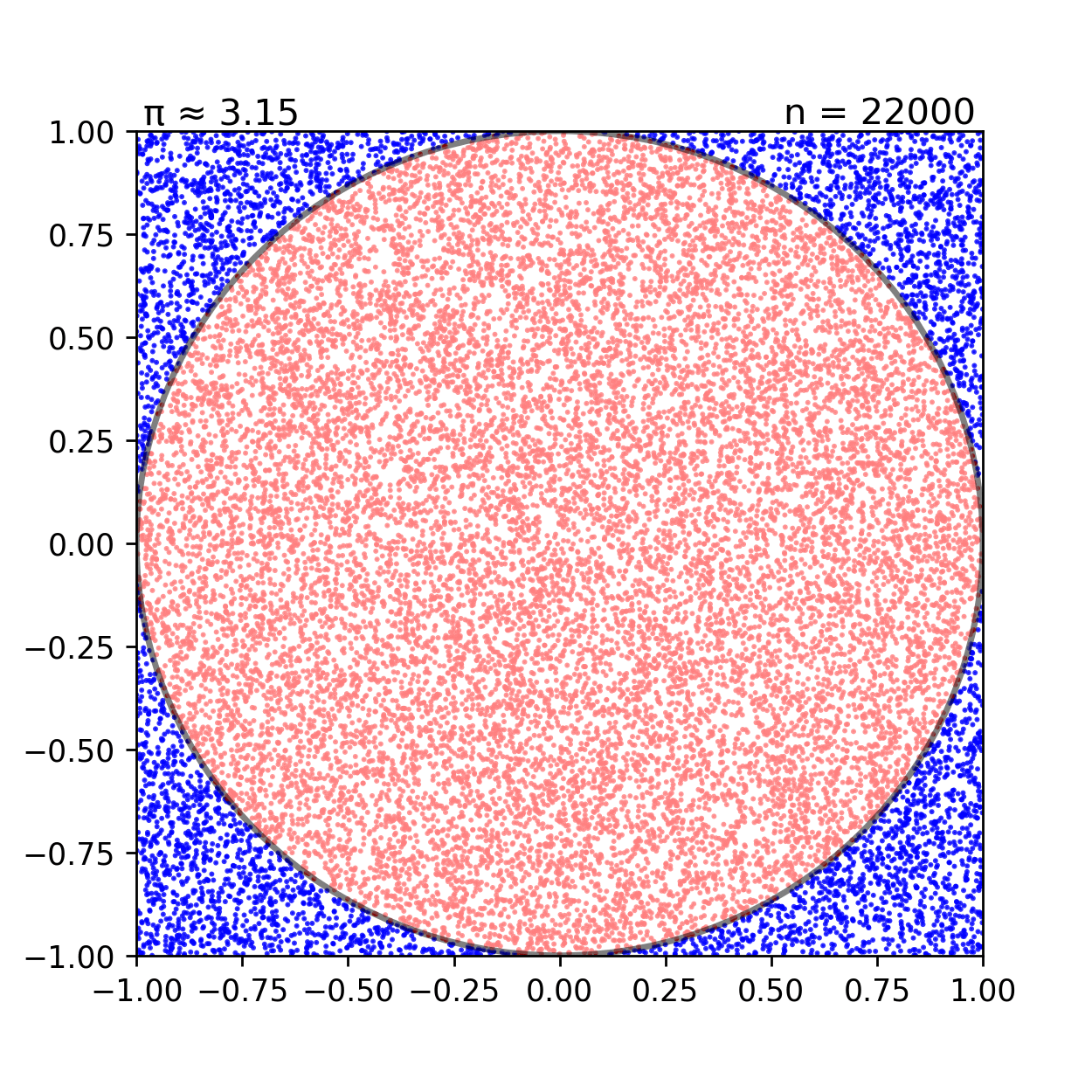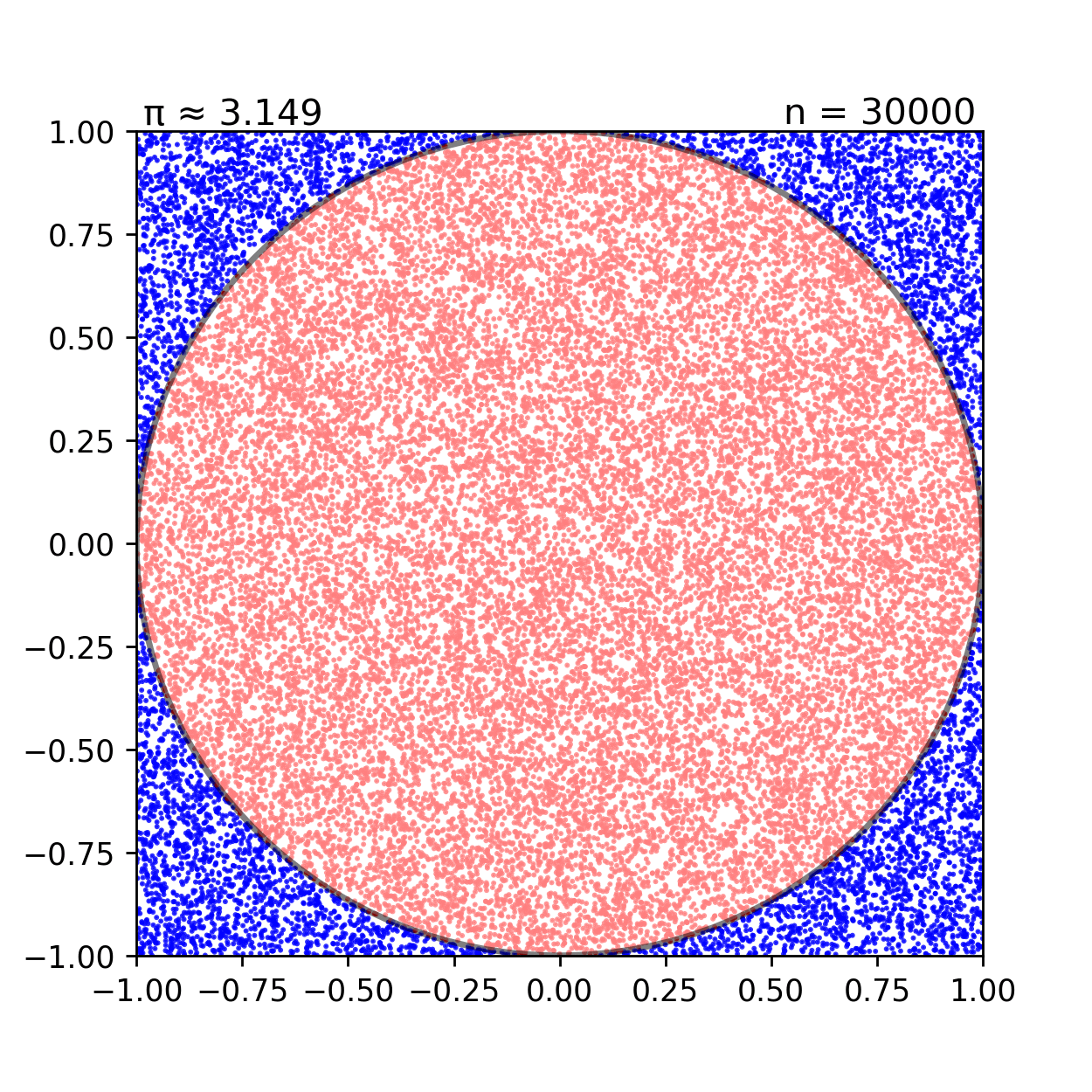
Фигура

  import random

  def monte_carlo_circle_area(radius, num_points=10000):
      inside_points = 0
      for _ in range(num_points):
          x = random.uniform(-radius, radius)
          y = random.uniform(-radius, radius)
          if x**2 + y**2 <= radius**2:
              inside_points += 1

      # Площадь квадрата, в который вписан круг = (2*radius)^2
      square_area = (2 * radius) ** 2
      circle_area = (inside_points / num_points) * square_area
      return circle_area

  # Пример использования
  radius = 5
  estimated_area = monte_carlo_circle_area(radius)
  print(f"Оцененная площадь круга с радиусом {radius}: {estimated_area}")

  #include <iostream>
  #include <vector>
  #include <cstdlib>
  #include <ctime>

  double monte_carlo_circle_area(double radius, int num_points = 10000) {
      int inside_points = 0;
      for (int i = 0; i < num_points; ++i) {
          double x = ((double)rand() / RAND_MAX) * 2 * radius - radius;
          double y = ((double)rand() / RAND_MAX) * 2 * radius - radius;
          if (x * x + y * y <= radius * radius) {
              inside_points++;
          }
      }

      // Площадь квадрата, в который вписан круг = (2*radius)^2
      double square_area = (2 * radius) * (2 * radius);
      double circle_area = (inside_points / (double)num_points) * square_area;
      return circle_area;
  }

  int main() {
      srand(time(0)); // Инициализация генератора случайных чисел
      double radius = 5;
      double estimated_area = monte_carlo_circle_area(radius);
      std::cout << "Оцененная площадь круга с радиусом " << radius << ": " << estimated_area << std::endl;
      return 0;
  }

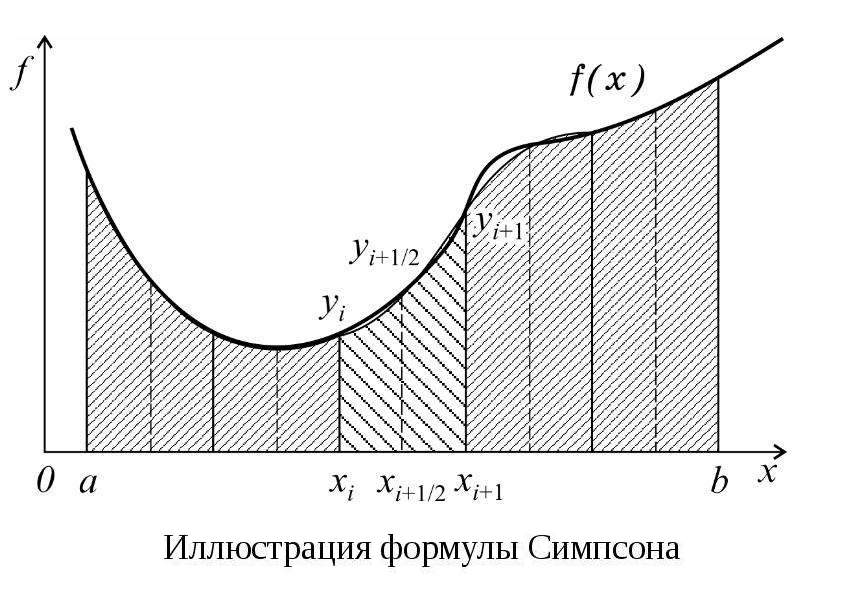
Формула Симпсона#

Формула Симпсона — это численный метод интегрирования, который основан на приближении функции квадратичной параболой. Он позволяет более точно вычислять определённые интегралы по сравнению с методом прямоугольников или трапеций.

  1. Разбиение отрезка интегрирования:
  2. Выбирается отрезок [a, b], на котором вычисляется интеграл.

  3. Делим его на n равных частей (где n — чётное число), получая узлы разбиения.

  4. Вычисление значений функции:

  5. Определяем значения функции в узлах разбиения x_0, x_1, ..., x_n .

  6. Применение формулы Симпсона:

\int_{a}^{b} f(x)dx \approx \frac{h}{3} \left( f(x_0) + 4 \sum_{i=1,3,5}^{n-1} f(x_i) + 2 \sum_{i=2,4,6}^{n-2} f(x_i) + f(x_n) \right)

где h = \frac{b - a}{n} .

  1. Уточнение результата:
  2. Увеличение числа узлов разбиения n повышает точность интегрирования.

Фигура

Пример Численное интегрирование функции:

import numpy as np

def simpson_rule(f, a, b, n):
    if n % 2 == 1:
        n += 1  # Делаем n четным
    h = (b - a) / n
    x = np.linspace(a, b, n+1)
    fx = f(x)

    integral = (h / 3) * (fx[0] + 4 * sum(fx[1:-1:2]) + 2 * sum(fx[2:-2:2]) + fx[-1])
    return integral

# Пример использования
f = lambda x: x**2  # Интегрируемая функция
result = simpson_rule(f, 0, 1, 10)
print(f"Приближённое значение интеграла: {result}")

#include <iostream>
#include <cmath>

double simpson_rule(double (*f)(double), double a, double b, int n) {
    if (n % 2 == 1) n++; // Делаем n четным
    double h = (b - a) / n;
    double sum = f(a) + f(b);

    for (int i = 1; i < n; i += 2)
        sum += 4 * f(a + i * h);

    for (int i = 2; i < n-1; i += 2)
        sum += 2 * f(a + i * h);

    return (h / 3) * sum;
}

double function(double x) {
    return x * x; // Интегрируемая функция
}

int main() {
    double result = simpson_rule(function, 0, 1, 10);
    std::cout << "Приближенное значение интеграла: " << result << std::endl;
    return 0;
}

Варианты#

Вариант Уравнения Картинка
Вариант 1 3 < x < 4
y = x^2 + 4
y = -x^2 - 4		 Вар 1
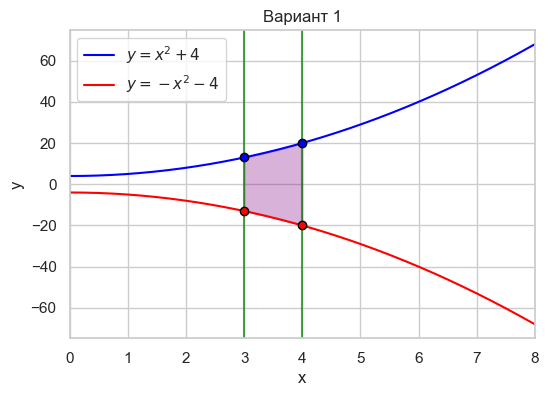Вариант 2 y = 2
y = x
y = -x + 6		 Вар 2
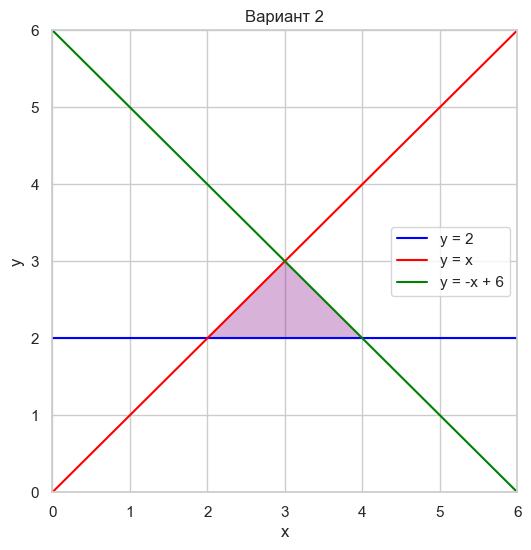Вариант 3 1 < x < 2
y = \sin(x) + 3
y = \sin(x) + 5		 Вар 3
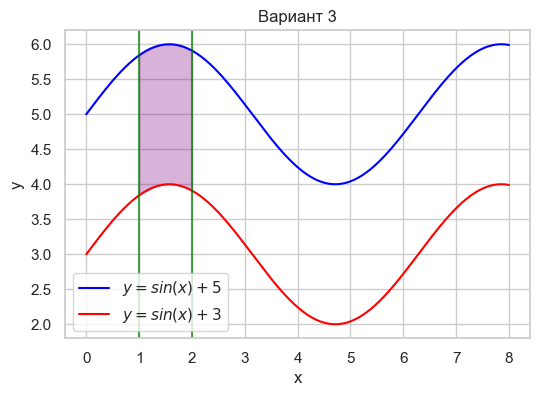Вариант 4 y = 2 - 0.5x
y = -2 + 0.5x
y = -2 - 0.5x
y = 2 + 0.5x		 Вар 4
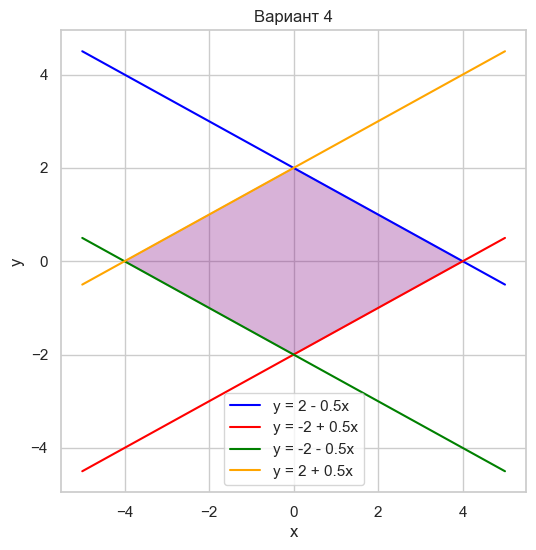Вариант 5 3 < x < 4
y = x^2 + 4x
y = -x^2 - 4x		 Вар 5
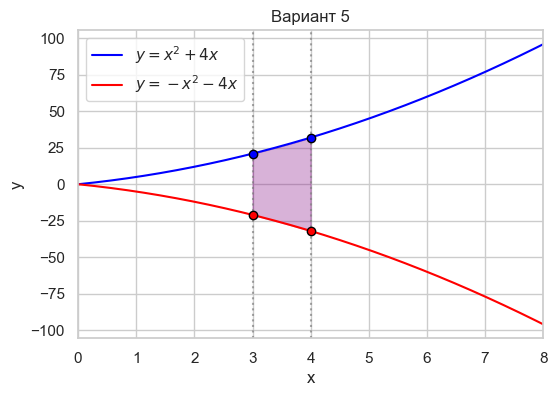Вариант 6 y = 3
y = -x + 8
y = x		 Вар 6
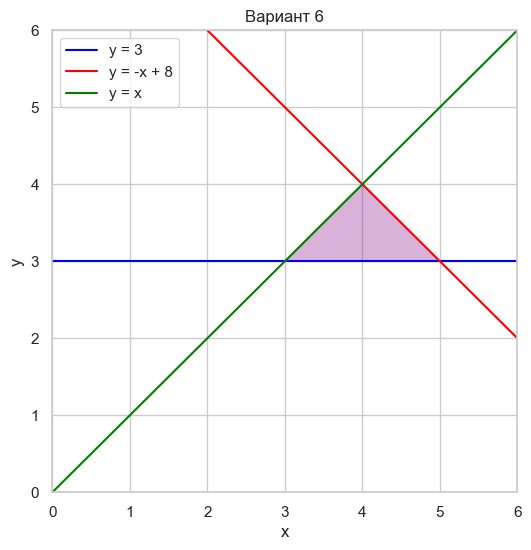Вариант 7 2 < x < 4
y = 2\sin(x) + 4
y = 0.5\cos(x) + 1		 Вар 7
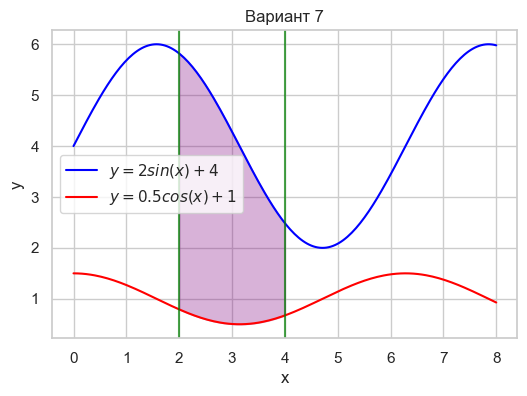Вариант 8 5 < x < 6
y = 2x^2 + 1
y = -2x^2 + 7		 Вар 8
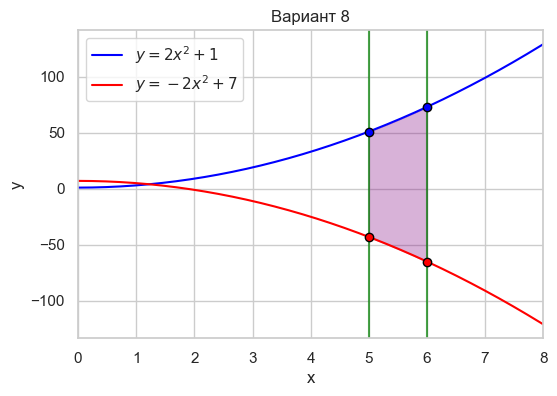Вариант 9 4 < x < 6
y = \sin(x)
y = \cos(x)
y = \sin(0.5x) - 0.5		 Вар 9
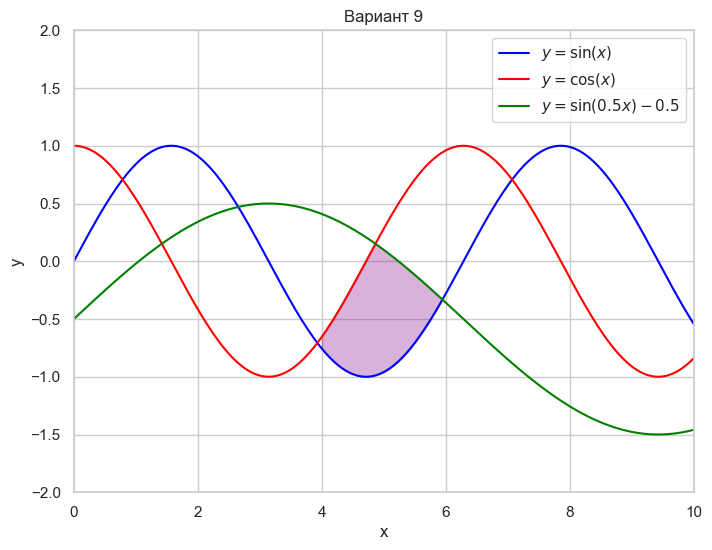Вариант 10 3 < x < 4
y = x^3 - 6x^2 + 4
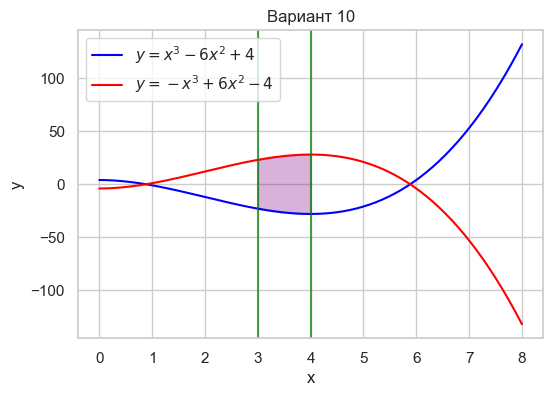y = -x^3 + 6x^2 - 4		 Вар 10
Вариант 11 y = 2x - 4
y = -2x + 12
y = 2x - 12
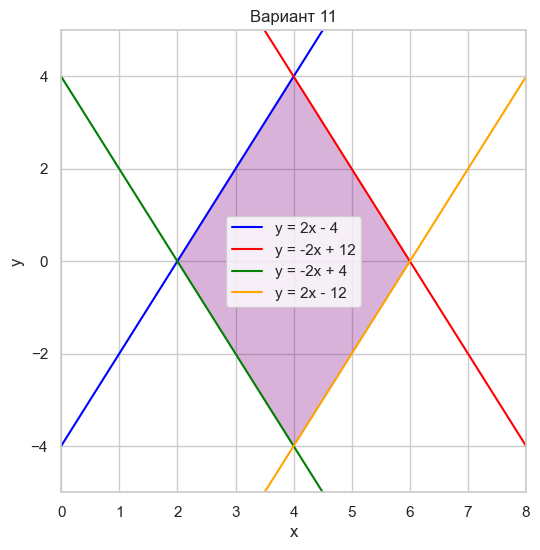y = -2x + 4		 Вар 11
Вариант 12 2 < x < 7
y = 3x^2 - 2
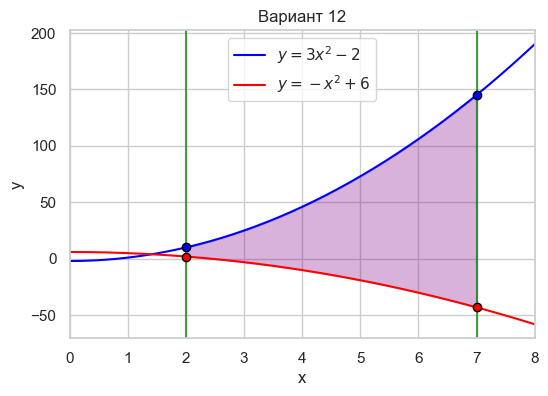y = -x^2 + 6		 Вар 12
Вариант 13 2 < x < 4
y = \sin(x)
y = \cos(x)
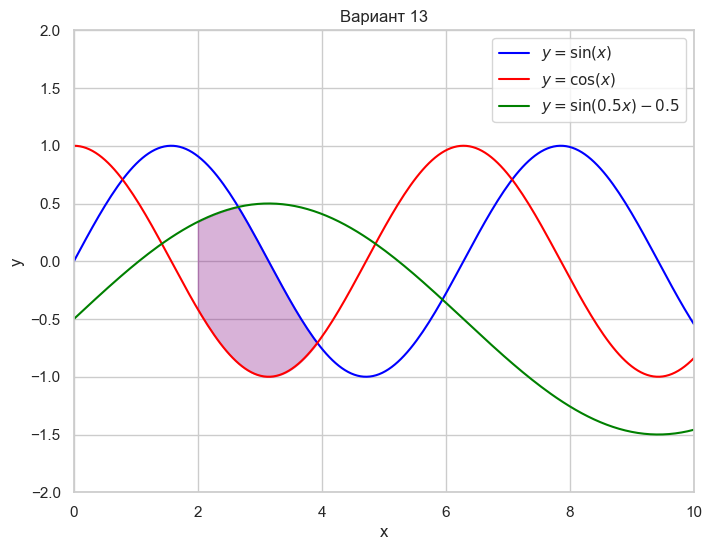y = \sin(0.5x) - 0.5		 Вар 13
Вариант 14 y = x^2
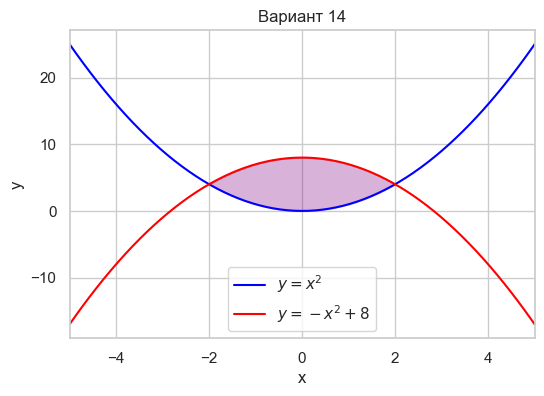y = -x^2 + 8		 Вар 14
Вариант 15 2 < x < 4
y = \cos(x) + 2
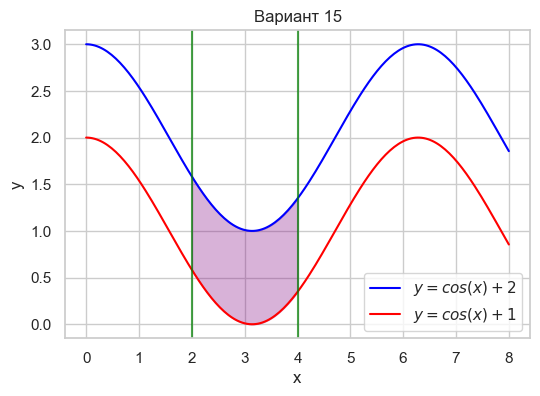y = \cos(x) + 1		 Вар 15
Вариант 16 y = 2
y = x
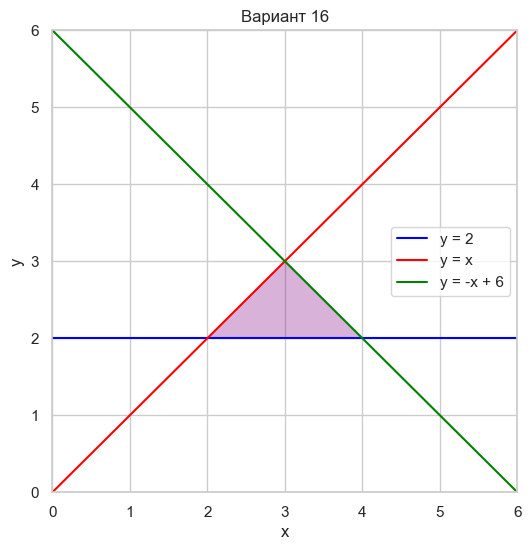y = -x + 6		 Вар 16
Вариант 17 3 < x < 6
y = x^3 - 12x^2 + 4
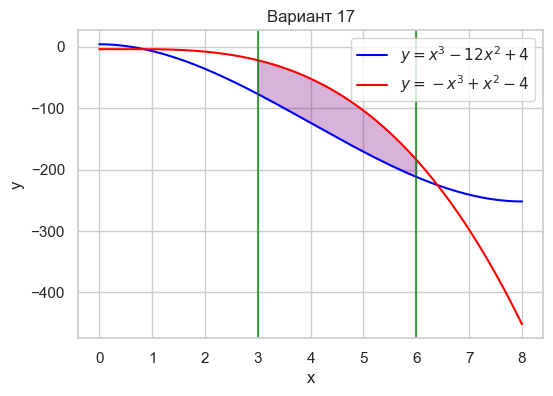y = -x^3 + x^2 - 4		 Вар 17
Вариант 18 4 < x < 5
y = \sin(x)
y = \cos(0.5x)
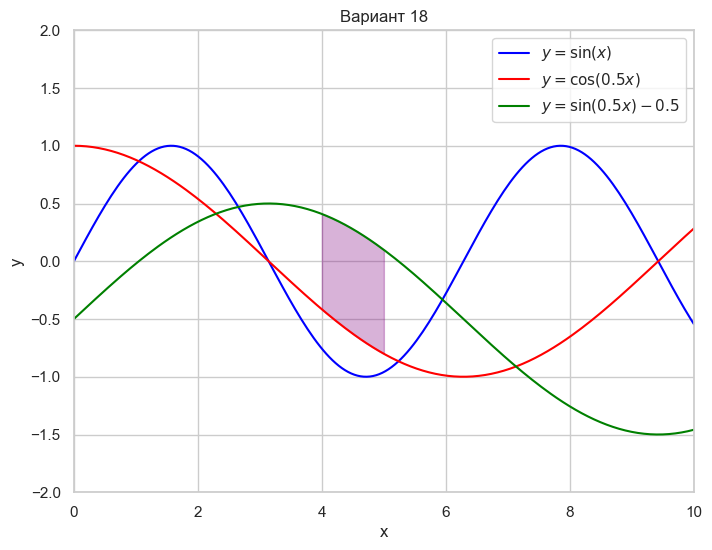y = \sin(0.5x) - 0.5		 Вар 18
Вариант 19 5 < x < 7
y = 3x^2 - 2x
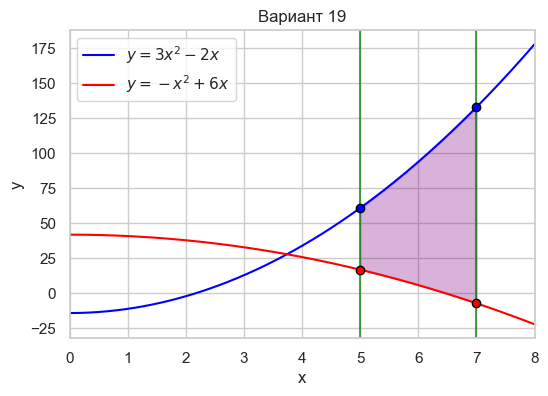y = -x^2 + 6x		 Вар 19
Вариант 20 1 < x < 2
y = 3\sin(x) + 5
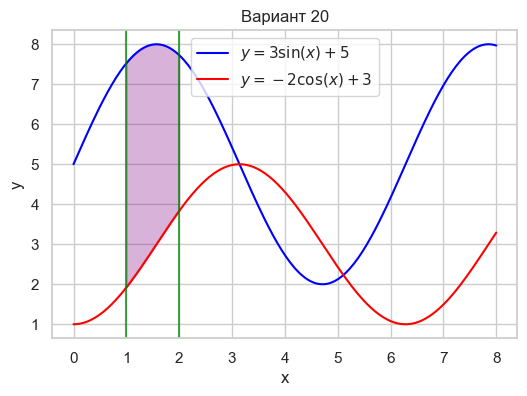y = -2\cos(x) + 3		 Вар 20
Вариант 21 x < 2
y = x^2
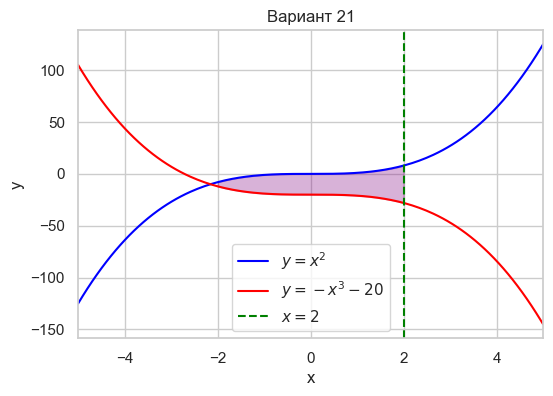y = -x^3 - 20		 Вар 21
Вариант 22 y = 3 - x
y = -3 + x
y = -3 - x
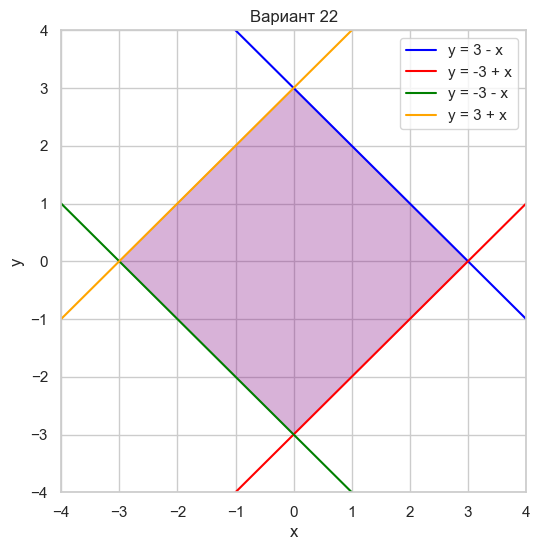y = 3 + x		 Вар 22
Вариант 23 6 < x < 8
y = \sin(x)
y = \cos(x)
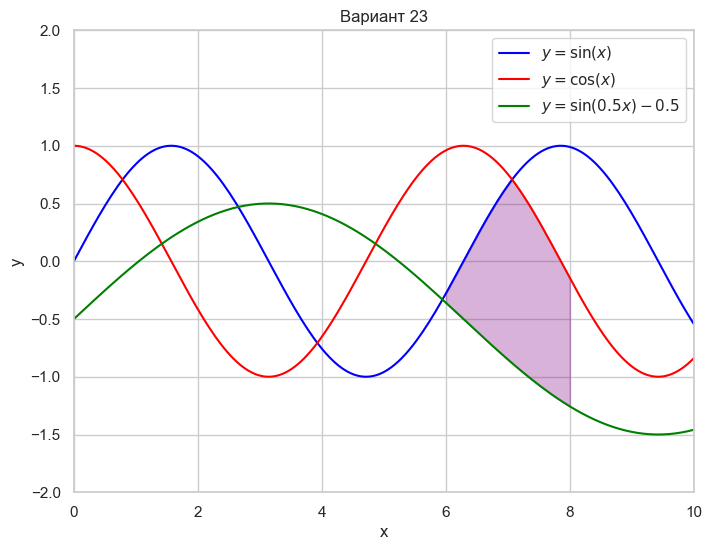y = \sin(0.5x) - 0.5		 Вар 23
Вариант 24 1 < x < 2
y = 3x^2 - 2x - 6
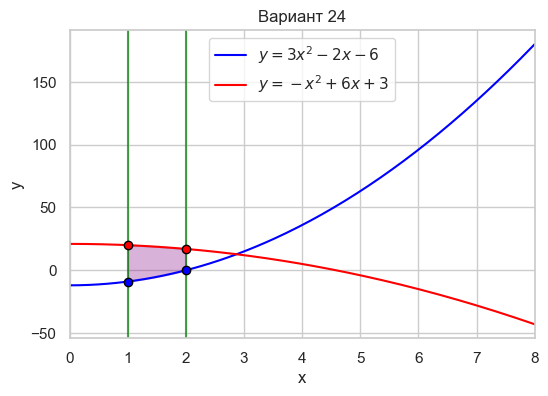y = -x^2 + 6x + 3		 Вар 24
Вариант 25 1 < x < 2
y = 3\cos(x) + 5
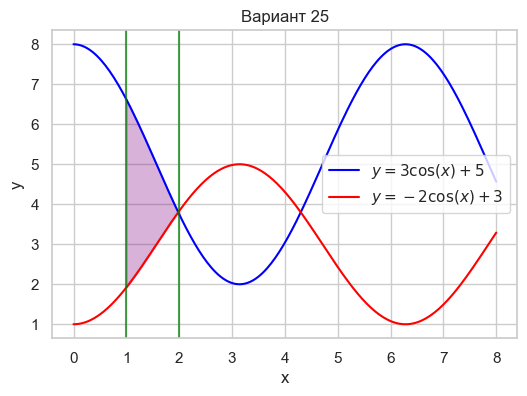y = -2\cos(x) + 3		 Вар 25
Вариант 26 y = 4
y = 3
x = 5
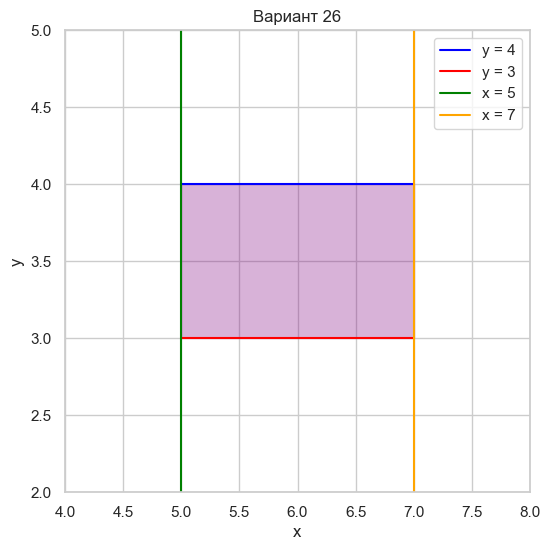x = 7		 Вар 26
Вариант 27 3 < x < 6
y = -x
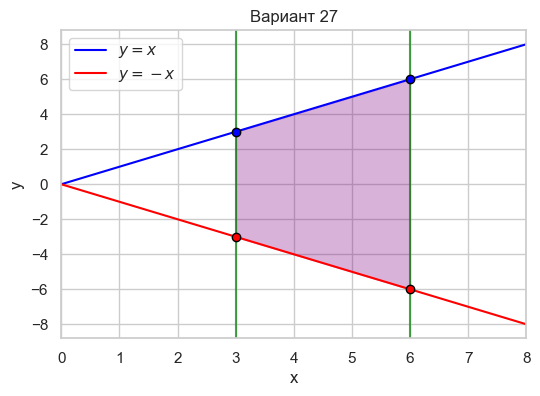y = x		 Вар 27
Вариант 28 y = 0.5x - 1
y = -0.5x + 7
y = 0.5x + 1
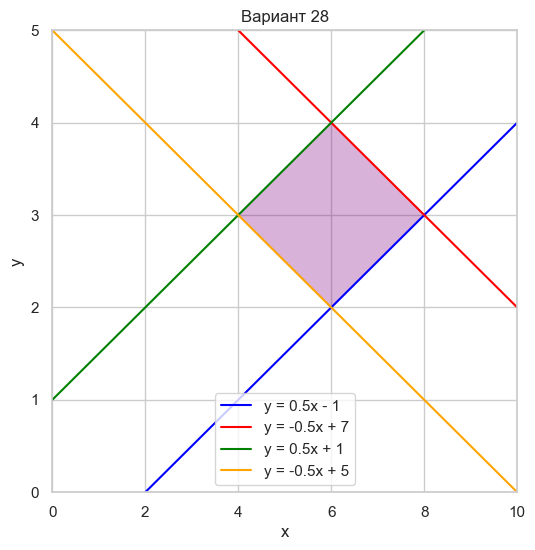y = -0.5x + 5		 Вар 28
Вариант 29 6 < x < 8
y = \sin(x)
y = \cos(0.5x)
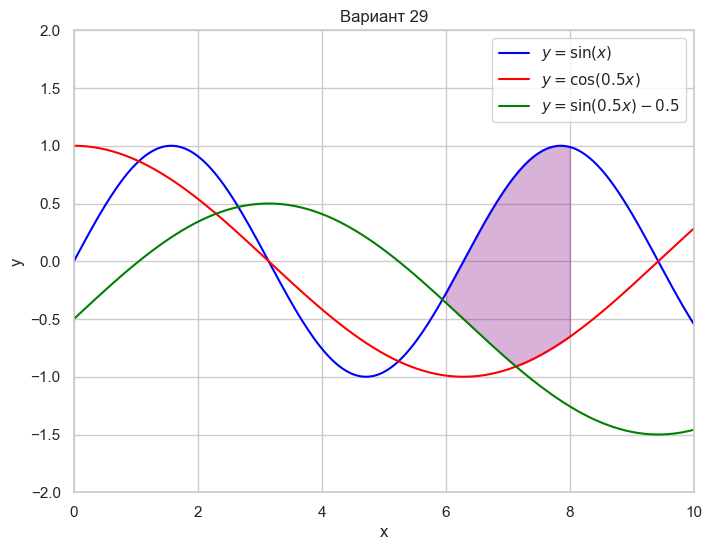y = \sin(0.5x) - 0.5		 Вар 29
Вариант 30 3 < x < 6
y = x^3 + 4x^2
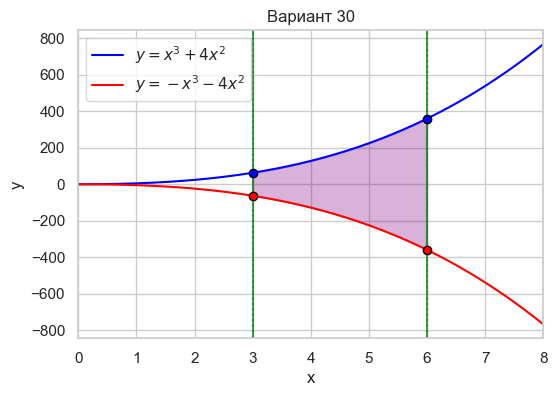y = -x^3 - 4x^2		 Вар 30