Практика 1 Оценка скорости работы алгоритмов

Оценка скорости работы алгоритма — важный навык при разработке эффективных решений. Для одной задачи обычно существует несколько вариантов решений, различающихся по скорости выполнения и сложности реализации. Основная цель — выбрать наиболее простое в реализации решение, которое укладывается в заданные ограничения по времени.

Этот процесс включает два аспекта:
- Теоретический — анализ количества абстрактных операций, выполняемых алгоритмом.
- Эмпирический — определение реального числа операций, которое может выполнить компьютер за фиксированный промежуток времени.

Тактовая частота процессора: что это такое и как она влияет на производительность?

При выборе процессора многие пользователи обращают внимание на его тактовую частоту. Это один из ключевых параметров, который часто рекламируют производители. Например, процессор с частотой 3,6 ГГц означает, что он выполняет 3,6 миллиарда тактов в секунду.

Но действительно ли чем выше тактовая частота, тем быстрее процессор? Давайте разберемся, как это работает на самом деле.

Что означает тактовая частота?

Тактовая частота — это количество синхронизирующих импульсов, поступающих в процессор за одну секунду. Эти импульсы задают ритм его работы, как метроном в музыке.

Однако тактовая частота не определяет напрямую скорость выполнения программ. Это связано с тем, что современные процессоры выполняют команды не по одной, а могут обрабатывать несколько инструкций одновременно благодаря конвейерной обработке и параллельному выполнению.

Abstract

Представьте себе конвейер на заводе. Если рабочие выполняют операции последовательно, то общая скорость работы будет зависеть от того, насколько быстро каждый выполняет свою часть задачи.  
Но если процесс можно разделить на несколько этапов и распределить работу между разными рабочими (или даже использовать несколько конвейеров одновременно), то завод сможет производить больше деталей за то же время.  
То же самое происходит в процессоре: его реальная производительность зависит не только от тактовой частоты, но и от множества других факторов.
Но если процесс можно разделить на несколько этапов и распределить работу между разными рабочими (или даже использовать несколько конвейеров одновременно), то завод сможет производить больше деталей за то же время.

То же самое происходит в процессоре: его реальная производительность зависит не только от тактовой частоты, но и от множества других факторов.

Какие факторы влияют на производительность процессора?

Рассмотрим основные факторы, которые определяют, насколько быстро процессор выполнит программу.

1 Архитектура процессора

Даже при одинаковой тактовой частоте разные поколения процессоров могут иметь разную производительность.
- Новые модели лучше оптимизированы для многозадачности и сложных вычислений.

2 Количество выполняемых команд за такт (IPC – Instructions Per Cycle)

• Одни процессоры могут выполнять 1 команду за такт, другие – 4 или больше.
• Чем выше IPC, тем больше работы процессор успевает выполнить за один тактовый цикл.

3 Количество ядер и потоков

• Современные процессоры могут иметь несколько ядер, каждое из которых выполняет свою часть программы.
• Многопоточные технологии позволяют распределять вычисления между потоками, повышая эффективность.

4 Размер и организация кэш-памяти

• Кэш-память играет ключевую роль в повышении производительности, поскольку позволяет процессору получать доступ к данным быстрее, чем из оперативной памяти.
• Больший размер кэша и улучшенная организация могут значительно ускорить выполнение задач.

5 Уровень поддержки новых наборов инструкций
- Процессоры поддерживают различные наборы инструкций (например, AVX, SSE).
- Оптимизация программного кода под новые инструкции может значительно увеличить скорость выполнения задач.

6 Технология предсказания ветвлений
- Предсказание ветвлений позволяет процессору заранее загружать нужные данные, уменьшая задержки при выполнении условных операторов и циклов.

7 Скорость работы оперативной памяти (RAM)
- Если процессор обрабатывает данные быстрее, чем получает их из RAM, возникает узкое место.
- Высокоскоростная RAM и технологии кэширования помогают избежать задержек.

Вывод

Тактовая частота – это **важный, но не единственный** показатель производительности процессора. Даже если один процессор работает на **4 ГГц**, а другой – на **3 ГГц**, это **не значит**, что первый всегда будет быстрее.

Реальная производительность зависит от архитектуры, количества ядер, скорости памяти и множества других факторов. Поэтому при выборе процессора важно учитывать **весь комплекс характеристик**, а не ориентироваться только на тактовую частоту.

Tip

Абсолютное большинство современных ПК построены на основе многоядерных процессоров. Такие процессоры физически позволяют исполнять несколько программных потоков параллельно. Благодаря этому несколько программ могут работать одновременно с минимальными задержками, а специально написанные программы могут совершать вычисления в разы быстрее (при условии, что они реализуют распределение задач по нескольким потокам). В то же время написание многопоточных программ требует специальных навыков и сопряжено с риском совершения различных ошибок.

Эмпирические показатели

Как было объяснено выше, точное предсказание того, сколько времени будет исполняться та или иная программа на конкретном компьютере, — практически невыполнимая задача. Однако можно начать с некоторых базовых ориентиров, а постепенно, с опытом, научиться «чувствовать» скорость и узкие места программ

Операция	Язык программирования	Число выполнений в секунду
Сложение 32-битных чисел	C++	5-6 млрд
	Python (РуРу)	1,8-1,9 млрд
	Python (CPython)	0,02-0,03 млрд
Перемножение 32-битных чисел	C++	0,8-0,9 млрд
	Python (РуРу)	0,6 млрд
	Python (CPython)	0,03 млрд

Примечание к таблице

Разумеется, приведенные ниже числа— лишь результат конкретных измерений на конкретных компьютерах, использованных автором книги. На других компьютерах, в том числе на тестирующих системах каких-либо соревнований, или в других условиях те же самые программы могут оказаться существенно быстрее или, наоборот, медленнее. Повторимся: эти числа даны лишь в качестве начальных ориентиров.

Из этой таблицы видно, почему при использовании языка программирования Python его реализация РуРу пользуется гораздо большей популярностью, чем CPython Более высокая скорость РуРу объясняется тем, что он содержит JIT-компилятор, преобразующий код на Python в машинный код во время его выполнения.

Асимптотическая оценка. Основы

Асимптотическая оценка — это способ оценивать вычислительную сложность алгоритмов, который абстрагируется от деталей архитектуры компьютера, от особенностей конкретной реализации и от конкретных входных данных. Ключевая идея этого подхода заключается в том, чтобы определить, с какой скоростью число операций, совершаемых конкретным алгоритмом, растет с увеличением входных данных. Этот подход не дает информации о том, сколько именно операций потребуется на конкретном входном наборе, зато он позволяет понять, какой алгоритм лучше остальных при достаточно больших входных данных

Вычислительная сложность

**Вычислительная сложность (алгоритмическая сложность)** — понятие, обозначающее функцию зависимости объема работы алгоритма от размера обрабатываемых данных.

Вычислительная сложность пытается ответить на центральный вопрос разработки алгоритмов: **как изменится время исполнения и объем занятой памяти в зависимости от размера входных данных**. С помощью вычислительной сложности также появляется возможность классификации алгоритмов согласно их производительности.

Подробнее про асиптотический анализ вы можете прочитать в конпекте лекции

Асимптотические нотация

Асимптотическая сложность алгоритма описывается соответствующей нотацией:

• О-нотация («O»-большое): описывает верхнюю границу времени (время выполнения «не более, чем…»).
• Омега-нотация («Ω»-большое): описывает нижнюю границу времени (время выполнения «не менее, чем…»).

Например,
O(n²) говорит о том, что алгоритм имеет квадратичное время выполнения относительно размера входных данных в качестве верхней оценки («O большое от эн квадрат»).

Каждая оценка может быть:

• Наилучшая: минимальная временная оценка.
• Наихудшая: максимальная временная оценка.
• Средняя: средняя временная оценка.

Допустим, имеется задача поиска элемента в массиве при полном переборе слева направо:

• Наилучшая оценка: O(1) — если искомый элемент окажется в начале списка.
• Наихудшая оценка: O(n) — если искомый элемент окажется в конце списка.
• Средняя оценка: O(n/2) ≈ O(n).

Проведем измерения на вашем компьютере воспользовавшись, следующим окошком:

Приведем код на С++ и Python для понимания процесса:

PythonC++

def linear_search(arr, target):
    for i, num in enumerate(arr):
        if num == target:
            return i
    return -1

#include <iostream>
#include <vector>

int linear_search(const std::vector<int>& arr, int target) {
    for (size_t i = 0; i < arr.size(); ++i) {
        if (arr[i] == target) {
            return i;
        }
    }
    return -1;
}

int main() {
    std::vector<int> arr = {1, 5, 3, 9, 2};
    int target = 3;
    int index = linear_search(arr, target);

    if (index != -1)
        std::cout << "Element found at index: " << index << std::endl;
    else
        std::cout << "Element not found" << std::endl;

    return 0;
}

Для асимптотической оценки необходимо проанализировать алгоритм, ответив на вопрос:
- есть ли ветвления?
- есть ли циклы? сколько раз выполняется цикл в лучшем/среднем/худшем случае?
- сколько операций следования?

Для подсчета сложности алгоритма следует пользовательстваться следующими правилами:

"Конструкция Следование"

Если несколько операций выполняются последовательно, то их общая вычислительная сложность определяется как сумма сложностей каждой операции:

$$T(n) = T_1(n) + T_2(n) + \dots + T_k(n)$$

Где $T_i(n)$ — трудоемкость $i$-го блока.

"Конструкция Ветвление"

Общая трудоемкость конструкции «ветвление» определяется с учетом вероятностей выполнения ветвей Then и Else:

$$T(n) = p \cdot T_1(n) + (1 - p) \cdot T_2(n)$$

Где:
- $T_1(n)$ — сложность выполнения блока Then,
- $T_2(n)$ — сложность выполнения блока Else,
- $p$ — вероятность выполнения блока Then.

"Конструкция Цикл"

Общая трудоемкость конструкции «цикл» определяется как сумма трудоемкостей тела цикла, выполненных заданное число раз:

$$T(n) = k \cdot T_{\text{body}}(n)$$

Где:
- $k$ — количество итераций цикла,
- $T_{\text{body}}(n)$ — трудоемкость одной итерации цикла.

Имея пример рассмотрим следующую задачу: Сформировать список всех возможных пар чисел одномерного массива

PythonC++

def generate_pairs(arr):
    pairs = []
    for i in range(len(arr)):
        for j in range(i + 1, len(arr)):
            pairs.append((arr[i], arr[j]))
    return pairs

arr = [1, 5, 3, 9, 2]
pairs = generate_pairs(arr)
print(pairs)

#include <iostream>
#include <vector>

std::vector<std::pair<int, int>> generate_pairs(const std::vector<int>& arr) {
    std::vector<std::pair<int, int>> pairs;
    for (size_t i = 0; i < arr.size(); ++i) {
        for (size_t j = i + 1; j < arr.size(); ++j) {
            pairs.push_back({arr[i], arr[j]});
        }
    }
    return pairs;
}

int main() {
    std::vector<int> arr = {1, 5, 3, 9, 2};
    std::vector<std::pair<int, int>> pairs = generate_pairs(arr);

    for (const auto& pair : pairs) {
        std::cout << "(" << pair.first << ", " << pair.second << ")" << std::endl;
    }

    return 0;
}

Асимптотическая оценка с одним параметром

Начнем с задач, сложность которых определяется одним входным параметром — обозначим его n. Например, один алгоритм может иметь асимптотическую сложность O(n), а другой — O(n²).

Но что означают эти обозначения?
- O(n) указывает на то, что алгоритм выполняется за линейное время, то есть количество операций порядка n.
- O(n²) обозначает квадратичное время работы, когда количество операций растет пропорционально n².

Приведем строгое определение.

Note

Асимптотическая сложность алгоритма — это `O(f(n))`, если существует положительная константа `c`, такая, что при любых `n` алгоритм выполняет не более `c * f(n)` операций.

Обозначение O широко используется в математике и читается как:
- O(n) — «о от эн»
- O(1) — «о от единицы»

Иногда уточняют «O большое», чтобы отличить от «o малое», но в контексте анализа алгоритмов последнее почти не используется.

Отличие от математического определения

Математическое определение `O` (введенное Бахманом в теории чисел) несколько отличается. В классическом определении вводится дополнительная константа `n₀`, и неравенство рассматривается только для `n > n₀`.  
Однако в анализе алгоритмов такое определение не всегда удобно, особенно при нескольких переменных.

Основные свойства асимптотической оценки

1. Анализируется поведение алгоритма в худшем случае
   Оценка строится для тех входных данных, на которых алгоритм выполняет максимальное число операций.

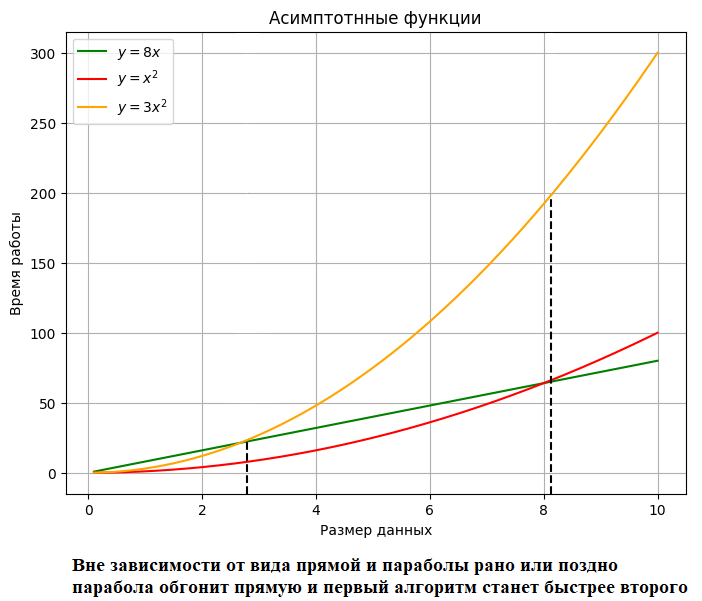
2. Оценка дается с точностью до константного множителя
   Например, O(5n) эквивалентно O(n), так как константы в асимптотическом анализе игнорируются. Это позволяет абстрагироваться от различий в архитектуре процессоров и особенностей языков программирования.

1. Учитывается поведение при больших n
   Несущественные слагаемые можно отбросить. Например, O(3n² + 2n + 1) ≡ O(n²), так как при достаточно больших n первое слагаемое доминирует.

2. Используется наиболее краткая запись

3. O(n), а не O(5n) или O(n + 10)
4. O(n²), а не O(3n² + 2n + 1)

5. O(n log n), а не O(n log n + n)

6. Асимптотическая оценка может быть неоптимальной
   Например, если алгоритм работает за O(n), его также можно записать как O(n²), но это будет избыточно. Поэтому стремятся находить наиболее точную асимптотическую оценку.

Эксперимент Практика

1 Откроем VS Studio -> Создание шаблона

2 Для python выбираете "Приложение для Python", для C++ "Консольное приложение"

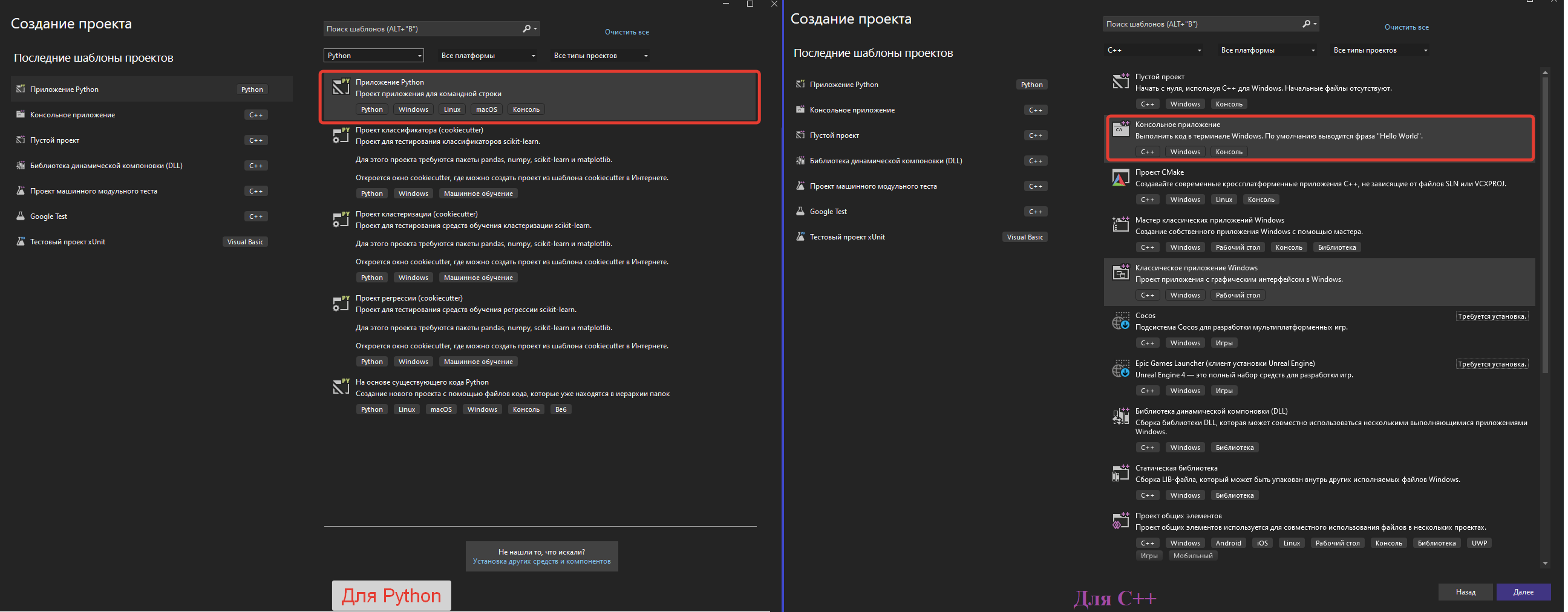
3 После создания проекта вы можете добавить Unit-tests следующим образом:
Для python в проводнике найти PythonApplication -> ПКМ -> Добавить -> Создать элемент -> Модульный тест на Python

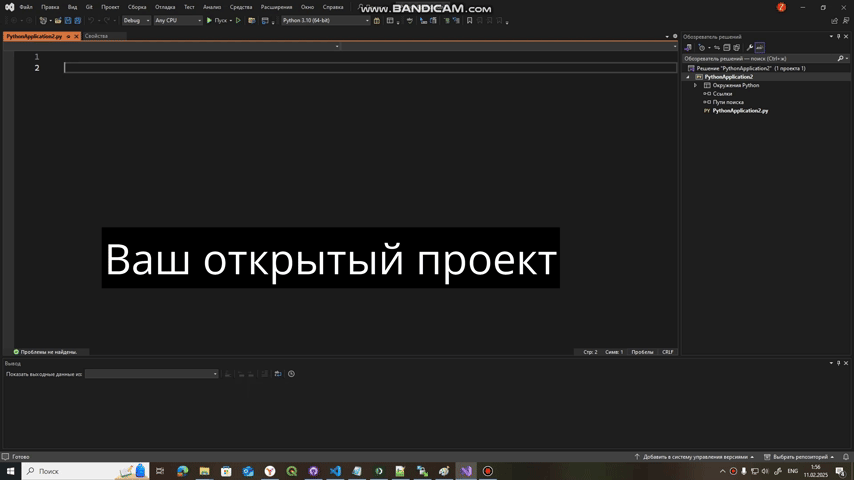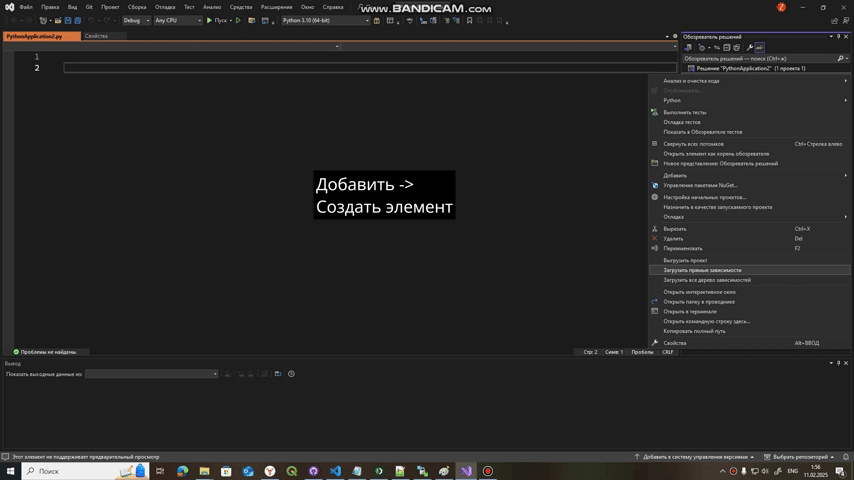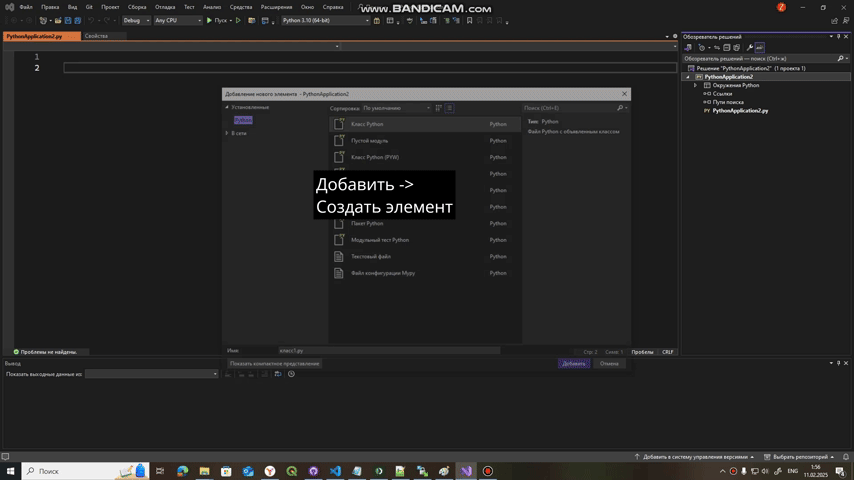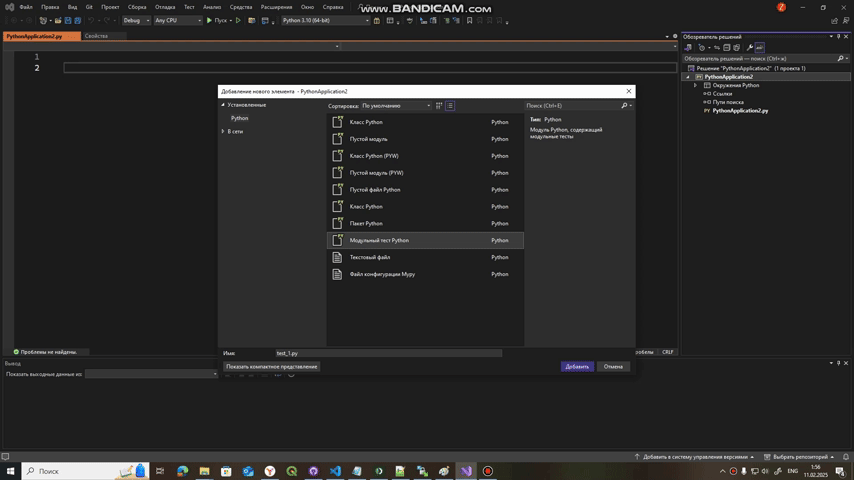
Для С++ нужно создать второй проект, поэтому вы нажимаете на Решение console application -> ПКМ-> Добавить -> Создать проект -> Проект машинного модульного теста

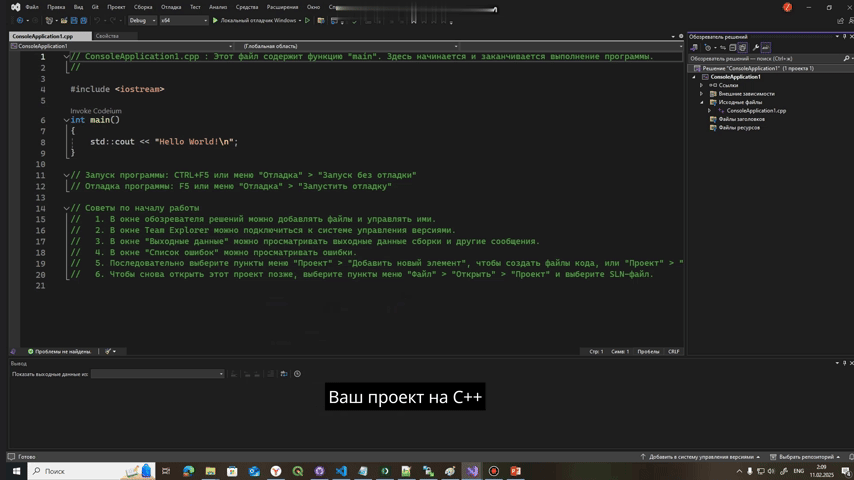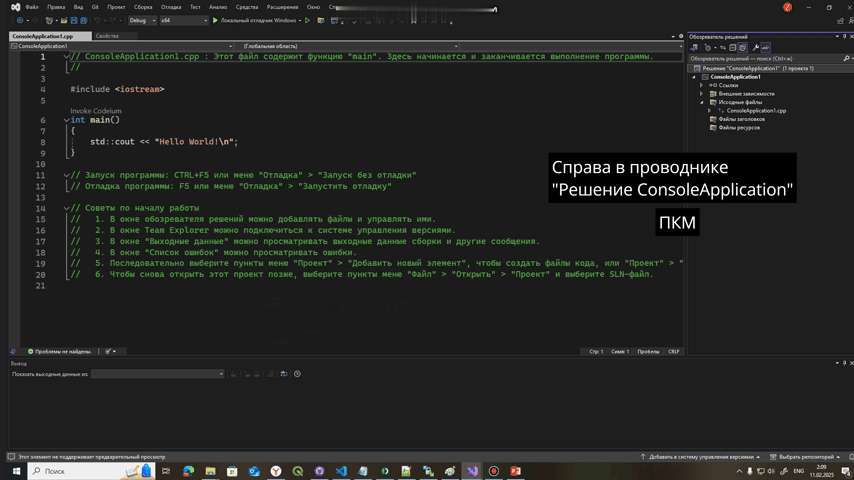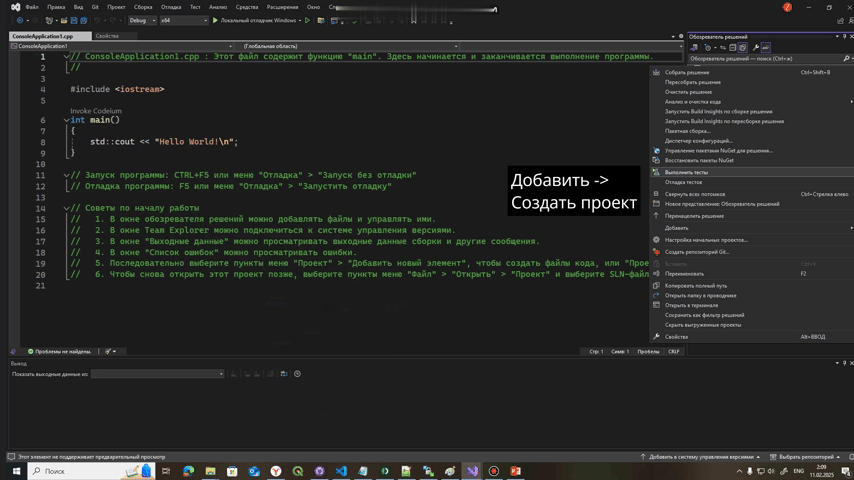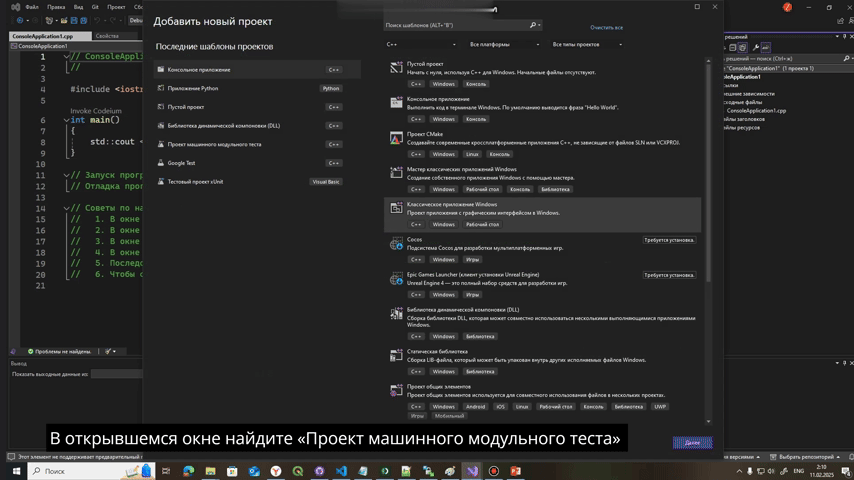
Оставим Unit-тесты в стороне, они нам еще понадобятся и напишем алгоритм поиска максимального элемента в массиве на с++ или python

Note

Реалзиовать функцию, которая ищет максимальный элемент массива (одномерного)

Note

Выполнить функицю 'func' с параметрами '*args', '**kw' и вернуть время выполнения в мс. (Поскольку ранее мы не передавали функцию внутрь функции, посмотрите как это делается)

PythonC++

def measure_execution_time(func, *args, **kw):
    start_time = time.time()  # Начинаем отсчет времени
    result = func(*args, **kw)  # Выполняем переданную функцию с аргументами
    end_time = time.time()  # Останавливаем отсчет времени
    execution_time = (end_time - start_time) * 1000  # Время в миллисекундах
    return result, execution_time

Аргументы для этой функции передаются через *args (неименованные аргументы) и **kw (именованные аргументы). Таким образом, мы можем передать любое количество аргументов и ключевых слов.

template <typename Func, typename... Args>
auto measure_execution_time(Func&& func, Args&&... args) {
    auto start_time = std::chrono::high_resolution_clock::now();  // Начинаем отсчет времени
    auto result = func(std::forward<Args>(args)...);  // Выполняем переданную функцию с аргументами
    auto end_time = std::chrono::high_resolution_clock::now();  // Останавливаем отсчет времени

    auto duration = std::chrono::duration_cast<std::chrono::milliseconds>(end_time - start_time);  // Вычисляем продолжительность в миллисекундах
    return std::make_pair(result, duration.count());  // Возвращаем результат и время выполнения
}

// Пример функции для тестирования
int example_function(int n) {
    int total = 0;
    for (int i = 0; i < n; ++i) {
        total += i;
    }
    return total;
}

int main() {
    auto [result, execution_time] = measure_execution_time(example_function, 1000000);
    std::cout << "Результат: " << result << ", Время выполнения: " << execution_time << " мс" << std::endl;
    return 0;
}

Шаблон typename... Args позволяет передавать любое количество аргументов в функцию, и они будут упакованы в пакет параметров. Внутри функции мы можем использовать их, развернув с помощью std::forward для правильной передачи аргументов в вызываемую функцию.

template: Объявление шаблона функции. В C++ шаблоны позволяют создавать функции или классы, которые могут работать с разными типами данных, не привязываясь к конкретному типу.

typename Func: Func — это параметр шаблона, который представляет тип функции (или callable объекта), который будет передан в шаблон. Когда вызывается такая функция, C++ автоматически подставит тип функции, который передан при вызове шаблона. Это позволяет функции работать с функциями или объектами, которые можно вызывать, например, функциями, лямбда-выражениями или объектами, переопределяющими оператор ().

typename... Args: Args — это параметр, который представляет собой список типов (пакет типов) для аргументов функции. ... в шаблоне обозначает параметры переменной длины. То есть, вы можете передавать любое количество параметров функции, и они будут автоматически обработаны как пакет типов.

Note

Выполните замеры для массива длины 10, 100, 1000

Unit-tests напоминание

Для проблем с Unit-tests Python

Если при запуске программы  высвечивается ошибка SyntaxError: (unicode error) 'utf-8' codec can't decode byte 0xd4 in position 5: invalid continuation byte, то впишите в начало файла следующу. строку `# coding=windows-1251`. Эта строка сообщает Python, что файл написан в кодировке windows-1251.

Чтобы пользоваться интерфейсов тестирования в VS откройте вкладку Тест -> Обозреватель тестов.

Обозреватель тестов может выполнять тесты из нескольких тестовых проектов в решении и из классов тестов, которые являются частью проектов рабочего кода. Тестовые проекты могут использовать различные платформы модульных тестов.
В обозревателе тестов можно группировать тесты в категории, фильтровать список тестов и создавать, сохранять и запускать списки воспроизведения тестов.

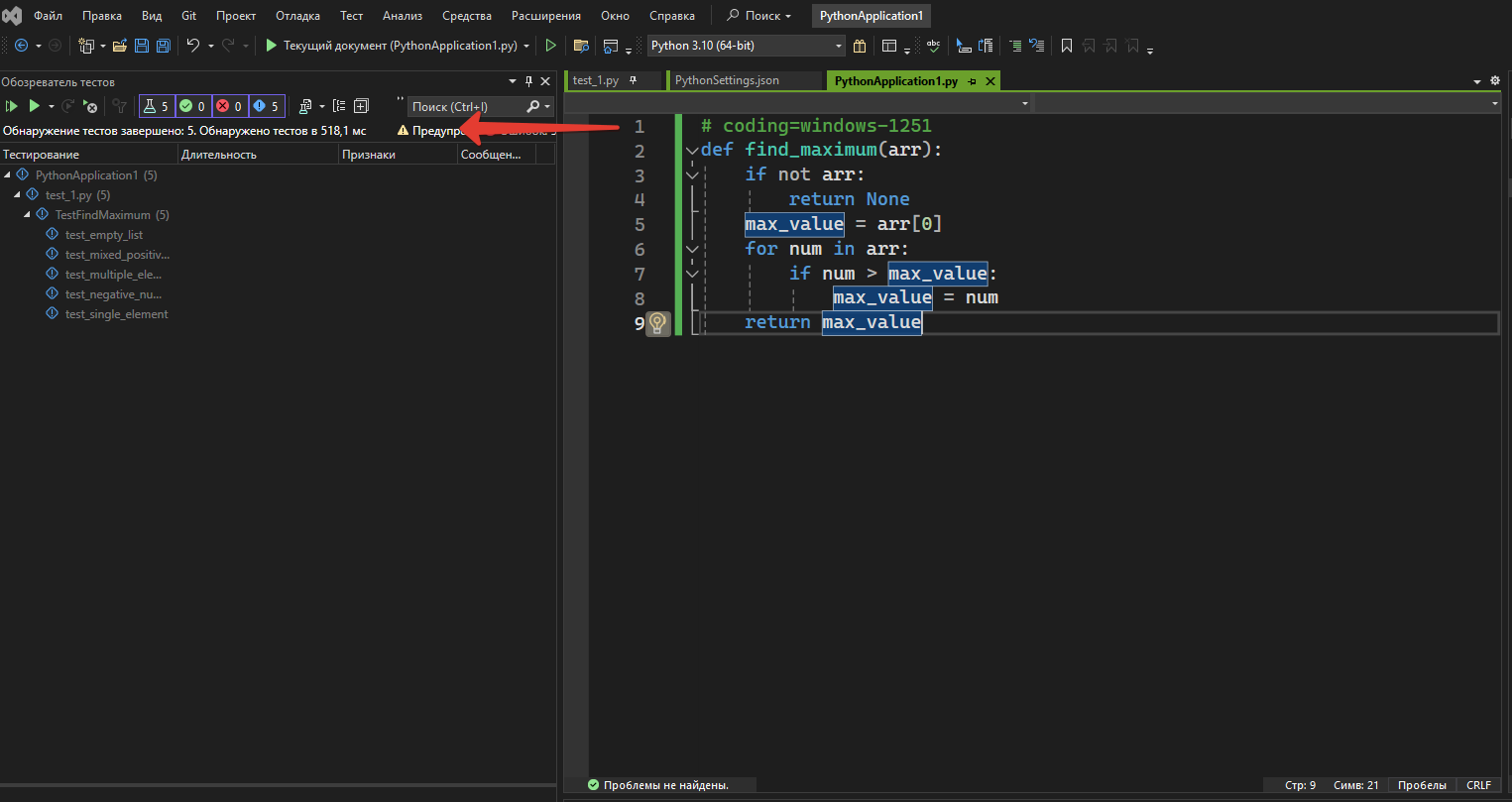
В С++ тесты начинают отображаться после Компиляции, а для Python необходимо добавить в проект файл с именем PythonSettings.json. Данный файл будет иметь следующую структуру:

    {
    "TestFramework": "unittest",
    "UnitTestRootDirectory": "./",
    "UnitTestPattern": "test_*.py"
    }

TestFramework: Указывает на фреймворк для тестирования. В этом случае, unittest — это стандартный фреймворк для Python.
UnitTestRootDirectory: Это корневая директория, где будут находиться тесты. В данном примере указано ./, что означает текущую директорию проекта.
UnitTestPattern: Шаблон имени тестовых файлов. В данном случае это test_*.py, что означает, что тесты должны быть в файлах, начинающихся с test_ и заканчивающихся на .py (например, test_example.py).
Если ваша программа на Python содержит папку src, отдельную от папки, содержащей ваши тесты, укажите путь к папке src с параметром SearchPaths в файле PythonSettings.json.

Python основные методыC++ основные методы

Основные методы

• assertEqual(a, b)
  Проверяет, равны ли значения a и b. Если не равны, тест не пройдет.

• assertNotEqual(a, b)
  Проверяет, что a не равно b. Если они равны, тест не пройдет.

• assertTrue(x)
  Проверяет, что выражение x истинно. Если оно ложно, тест не пройдет.

• assertFalse(x)
  Проверяет, что выражение x ложно. Если оно истинно, тест не пройдет.

• assertIs(a, b)
  Проверяет, что a и b указывают на один и тот же объект.

• assertIsNot(a, b)
  Проверяет, что a и b не указывают на один и тот же объект.

• assertIsNone(x)
  Проверяет, что x является None.

• assertIsNotNone(x)
  Проверяет, что x не является None.

• assertRaises(exception, callable, *args, kwargs)
  Проверяет, что при вызове callable с аргументами args и kwargs будет выброшено исключение exception.

• assertAlmostEqual(a, b, places=7)
  Проверяет, что a и b равны с точностью до places десятичных знаков.

• assertNotAlmostEqual(a, b, places=7)
  Проверяет, что a и b не равны с точностью до places десятичных знаков.

Дополнительные методы для настройки и завершения тестов

• setUp()
  Этот метод выполняется перед каждым тестом в классе. Используется для инициализации объектов или установки начальных условий.

• tearDown()
  Этот метод выполняется после каждого теста в классе. Используется для очистки или завершения работы с ресурсами.

import unittest
from PythonApplication2 import find_maximum
class TestFindMaximum(unittest.TestCase):

    def test_empty_list(self):
        self.assertIsNone(find_maximum([]), "Должно возвращать None для пустого списка")

    def test_single_element(self):
        self.assertEqual(find_maximum([5]), 5, "Должно возвращать элемент сам по себе для списка с одним элементом")

    def test_multiple_elements(self):
        self.assertEqual(find_maximum([1, 2, 3, 4, 5]), 5, "Должно возвращать максимальное значение в списке")

    def test_negative_numbers(self):
        self.assertEqual(find_maximum([-1, -2, -3, -4]), -1, "Должно возвращать максимальное значение в списке с отрицательными числами")

    def test_mixed_positive_negative(self):
        self.assertEqual(find_maximum([5, -1, 9, -3]), 9, "Должно возвращать максимальное значение в списке с положительными и отрицательными числами")

if __name__ == '__main__':
    unittest.main()

Основные методы

• aAssert::Equal(a, b)
  Проверяет, равны ли значения a и b. Если не равны, тест не пройдет.

• Assert::NotEqual(a, b)
  Проверяет, что a не равно b. Если они равны, тест не пройдет.

• Assert::True(x)
  Проверяет, что выражение x истинно. Если оно ложно, тест не пройдет.

• Assert::False(x)
  Проверяет, что выражение x ложно. Если оно истинно, тест не пройдет.

• Assert::Is(a, b)
  Проверяет, что a и b указывают на один и тот же объект.

• Assert::IsNot(a, b)*
  Проверяет, что a и b не указывают на один и тот же объект.

• Assert::IsNone(x)
  Проверяет, что x является None.

• Assert::IsNotNone(x)
  Проверяет, что x не является None.

• Assert::Raises(exception, callable, *args, kwargs)
  Проверяет, что при вызове callable с аргументами args и kwargs будет выброшено исключение exception.

#include "pch.h"
#include "CppUnitTest.h"
#include "../ConsoleApplication1/ConsoleApplication1.cpp"

using namespace Microsoft::VisualStudio::CppUnitTestFramework;

namespace UnitTest1
{
    TEST_CLASS(UnitTest1)
    {
    public:

        TEST_METHOD(TestMethod1)
        {
            // Пример теста для find_maximum
            std::vector<int> arr = { 1, 5, 3, 9, 2 };
            int result = find_maximum(arr);
            Assert::AreEqual(result, 9);  // Проверяем, что максимальное значение равно 9
        }

        TEST_METHOD(TestMethod2)
        {
            // Тест для пустого массива
            std::vector<int> arr = {};
            int result = find_maximum(arr);
            Assert::AreEqual(result, std::numeric_limits<int>::min());  // Проверяем, что возвращается минимальное значение для int
        }

        TEST_METHOD(TestMethod3)
        {
            // Тест для массива с одним элементом
            std::vector<int> arr = { 10 };
            int result = find_maximum(arr);
            Assert::AreEqual(result, 10);  // Проверяем, что максимальное значение равно 10
        }
    };
}