Задача Коммивояжера подходы и решения#

Исторический экскурс#

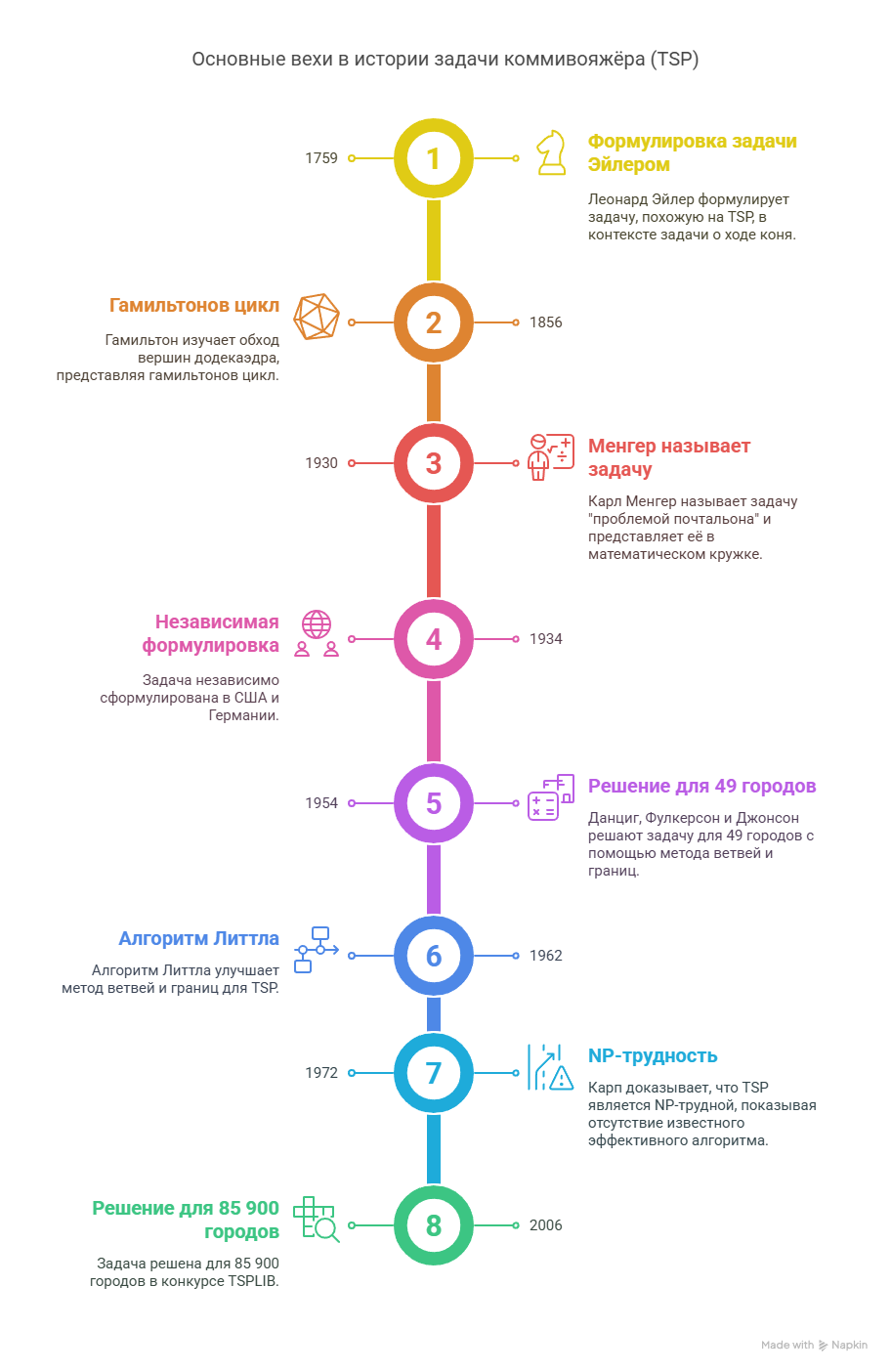
Первые идеи, схожие с задачей коммивояжёра, можно обнаружить ещё в XIX веке. В 1832 году ирландский математик Уильям Гамильтон обсуждал пути, проходящие через определённые вершины графа, что позже вылилось в изучение гамильтоновых циклов. Однако формулировка задачи о нахождении кратчайшего маршрута для обхода всех точек появилась только в XX веке.

Важный этап в развитии задачи коммивояжёра наступил в 1950–1960 гг., когда её исследованием занялись американские и европейские ученые. Здесь особенно выделяются Джордж Данциг, Делберт Рей Фалкерсон и Селмер Джонсон, работавшие в институте RAND Corporation. В 1954 году они сформулировали задачу как задачу дискретной оптимизации и применили метод отсечений (алгоритм Гомори) для решения варианта задачи коммивояжёра с 49 городами, обосновав оптимальность найденного маршрута.

В это же время появились родственные постановки. В 1962 году китайский математик Мэй-Ку Куан сформулировал так называемую задачу китайского почтальона, в которой требовалось пройти по каждой улице города хотя бы один раз минимальным путём. Это задание отличалось от классической задачи коммивояжёра, но обострило интерес к оптимизационным задачам на графах.

В 1960–1970 гг. исследование задачи коммивояжёра шло в двух направлениях: теоретическом (развитие алгоритмов, доказательство вычислительной сложности) и прикладном (оптимизация маршрутов в экономике, биологии, химии, информатике). Важнейшим теоретическим событием стало доказательство NP-полноты задачи поиска гамильтонова пути американским информатиком Ричардом Мэннингом Карпом в 1972 году, что автоматически устанавливало NP-трудность задачи коммивояжёра.

Особенно плодотворными были 1970–1980-е годы. Мартин Гретчел, Манфред Падберг, Джованни Ринальди и другие ученые добились крупных успехов в решении задачи на практике, применяя новые методы — такие как деление плоскостью и метод ветвей и границ. В результате им удалось найти оптимальное решение задачи коммивояжёра для 2392 городов.

Развитие вычислительной техники и алгоритмов позволило достигать всё больших рекордов. В апреле 2006 года было установлено решение задачи коммивояжёра для случая с 85 900 городами. Однако это далеко не предел: современные эвристические и точные методы позволяют эффективно работать с задачами, содержащими миллионы вершин.

Сегодня задача коммивояжёра остаётся не только классическим примером комбинаторной оптимизации, но и тестовой площадкой для новых вычислительных методов. Её приложения охватывают логистику, робототехнику, планирование маршрутов дронов, оптимизацию сборки цепочек в биоинформатике и многое другое.

Граф алгоритма

Формальная постановка задачи#

Задача коммивояжера (TSP) заключается в нахождении оптимального пути, который проходит через все города, посещая каждый город один раз и возвращается в исходную точку. Пусть дан граф $G = (V, E)$ , где:

$V = \{v_1, v_2, \dots, v_n\}$ — множество городов,
$E = \{e_{ij}\}$ — множество рёбер, где $e_{ij}$ — расстояние между городами $v_i$ и $v_j$ .

Задача сводится к нахождению минимального пути $C$ , который соединяет все города, то есть находит такой цикл, который минимизирует суммарное расстояние:

$C = \{v_1, v_2, \dots, v_n, v_1\}$

Задача может быть математически выражена как минимизация функции стоимости пути $f(x)$ , где $x$ — последовательность городов:

$f(x) = \sum_{i=1}^{n-1} d(x_i, x_{i+1}) + d(x_n, x_1)$

где $d(x_i, x_{i+1})$ — расстояние между городами $x_i$ и $x_{i+1}$ .

Цель задачи:

$\min_{x} f(x)$

где $x$ — это перестановка всех городов.

Задача коммивояжера является NP-трудной задачей, то есть её решение требует экспоненциального времени для поиска оптимального пути при увеличении количества городов.

Методы решения#

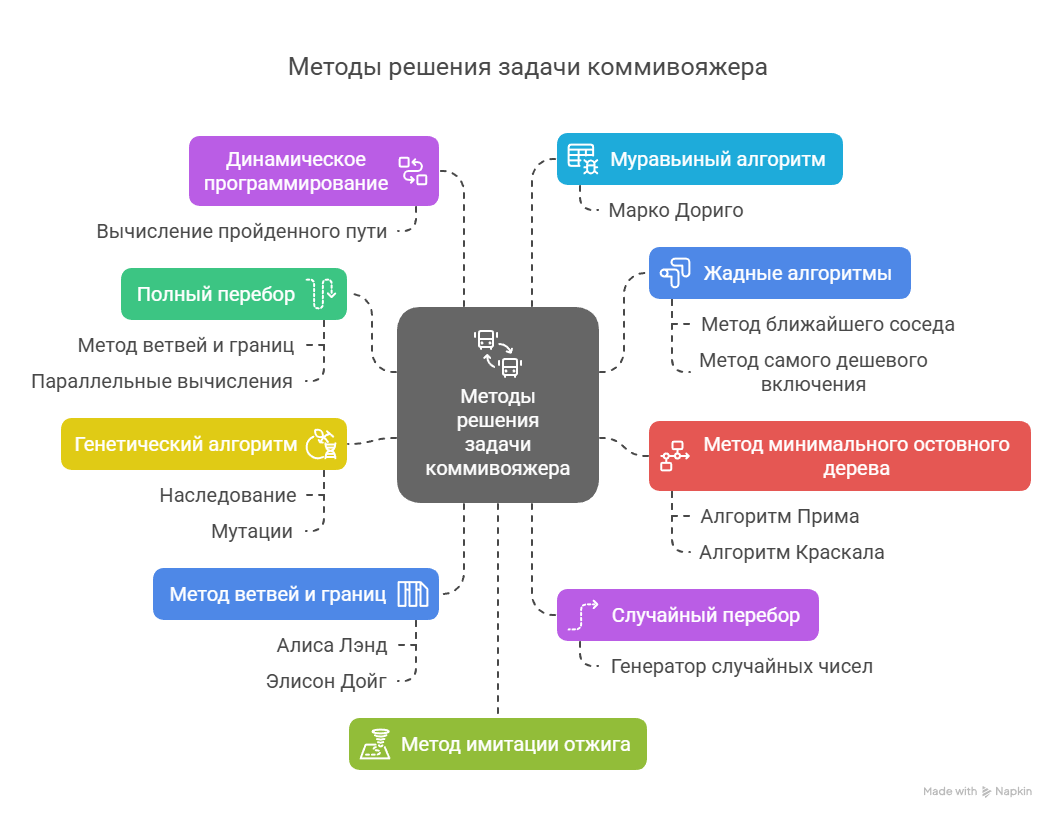
Методы решения задачи коммивояжера довольно разнообразны и различаются применяемым инструментарием, точностью находимого решения и сложностью требуемых вычислений. Вот лишь некоторые из них:

Полный перебор (метод «грубой силы», англ. «Brute Force») — заключается в последовательном рассмотрении всех возможных маршрутов и выборе из них оптимального. Метод самый простой и точный, но неэффективный и при большом количестве городов его применение становится затруднительным ввиду значительных затрат времени и ресурсов на перебор огромного количества вариантов решения задачи. Для ускорения и повышения эффективности полного перебора используются различные приемы: метод ветвей и границ, параллельные вычисления, радужные таблицы.
Случайный перебор — в этом случае вычисляются не все возможные варианты маршрута, а лишь некоторые выбранные в случайном порядке (например, с помощью генератора случайных чисел). Из рассмотренных вариантов затем выбирается наилучший. Конечно, вероятнее всего полученное решение не будет оптимальным (впрочем, оно не будет и самым худшим), но зато данный метод требует меньших затрат времени и вычислительных ресурсов, а потому в некоторых случаях его применение оправдано.
Динамическое программирование — ключевая идея заключается в вычислении и запоминании пройденного пути от исходного города до всех остальных, последующем прибавлении к нему расстояний от текущих городов до оставшихся, и так далее. По сравнению с полным перебором этот метод позволяет существенно сократить объем вычислений.
Жадные алгоритмы (англ. «Greedy») — основаны на нахождении локально оптимальных решений на каждом этапе вычислений и допущении, что найденное таким образом итоговое решение будет глобально оптимальным. Т. е. на каждой итерации выбирается лучший участок пути, который включается в итоговый маршрут. Метод простой, но его большой недостаток в том, что может возникнуть ситуация, когда окажется, что начальная и конечная точки маршрута разнесены далеко друг от друга и их придется соединять длинным отрезком пути, что значительно снизит эффективность решения. К жадным алгоритмам относятся: метод ближайшего соседа (англ. «Nearest Neighbour»), модифицированный метод ближайшего соседа (англ. «Double Ended Nearest Neighbour»), метод самого дешевого включения и т. д.
Метод минимального остовного дерева — поиск маршрута ведется на графе. Для нахождения оптимального пути применяются различные инструменты: алгоритм Прима, алгоритм Краскала, алгоритм Борувки.
Метод имитации отжига — один из численных методов Монте-Карло.
Метод эластичной сети — каждый из возможных маршрутов рассматривается как отображение окружности на плоскость.
Муравьиный алгоритм — эвристический метод, основанный на моделировании поведения муравьев, ищущих пути от своей колонии к источникам пищи. Первую версию такого алгоритма предложил доктор наук Марко Дориго в 1992 году. Этот метод позволяет относительно быстро найти хорошее, но не обязательно оптимальное решение.
Генетический алгоритм — еще один эвристический метод, заключающийся в случайном подборе и комбинировании исходных параметров с использованием механизмов имитирующих естественный отбор в процессе эволюции (наследование, мутации, кроссинговер). Несмотря на довольно широкие возможности применения (и не только в логистике), этот метод часто становится объектом критики.
Метод ветвей и границ — один из методов дискретной оптимизации, являющийся развитием метода полного перебора, но отличающийся от него отсевом в процессе вычисления подмножеств неэффективных решений. Впервые был предложен в 1960 году английским профессором Алисой Лэнд и австралийским математиком Элисон Дойг.

Граф алгоритма

Полный перебор#

from itertools import permutations

def calculate_distance(route, distance_matrix):
    return sum(distance_matrix[route[i]][route[i+1]] for i in range(len(route)-1)) + distance_matrix[route[-1]][route[0]]

def brute_force_tsp(distance_matrix):
    n = len(distance_matrix)
    cities = list(range(n))
    min_distance = float('inf')
    best_route = None

    for perm in permutations(cities):
        current_distance = calculate_distance(perm, distance_matrix)
        if current_distance < min_distance:
            min_distance = current_distance
            best_route = perm

    return best_route, min_distance

# Пример использования
distance_matrix = [
    [0, 10, 15, 20],
    [10, 0, 35, 25],
    [15, 35, 0, 30],
    [20, 25, 30, 0]
]

route, distance = brute_force_tsp(distance_matrix)
print("Лучший маршрут:", route)
print("Кратчайшее расстояние:", distance)

Разбор кода:
- Используется itertools.permutations для генерации всех возможных маршрутов.
- Функция calculate_distance() вычисляет длину маршрута, включая возвращение в начальный город.
- Перебираются все возможные перестановки городов, выбирается маршрут с минимальным расстоянием.

Сложность:
Полный перебор имеет факториальную сложность O(n!), так как рассматриваются все возможные маршруты.
Это делает алгоритм непрактичным для больших n, например, уже при n=10 количество возможных маршрутов достигает 3,628,800.

✅ Достоинства решения:
- Гарантированно находит оптимальное решение.
- Простая реализация.

❌ Недостатки решения:
- Экспоненциальная сложность — не подходит для больших входных данных.
- Требует хранения всех возможных маршрутов, что потребляет много памяти.

Жадные алгоритмы#

Простые эвристики, такие как «ближайший сосед» (Nearest Neighbor), позволяют быстро находить приближённые решения, но не гарантируют их оптимальность.

def nearest_neighbor_tsp(distance_matrix):
    n = len(distance_matrix)
    visited = [False] * n
    route = [0]  # Начинаем с первого города
    visited[0] = True

    for _ in range(n - 1):
        last_city = route[-1]
        nearest_city = min(
            [(i, distance_matrix[last_city][i]) for i in range(n) if not visited[i]],
            key=lambda x: x[1]
        )[0]
        route.append(nearest_city)
        visited[nearest_city] = True

    route.append(0)  # Возвращаемся в начальный город
    total_distance = sum(distance_matrix[route[i]][route[i+1]] for i in range(n))
    return route, total_distance

# Пример использования
route, distance = nearest_neighbor_tsp(distance_matrix)
print("Жадный маршрут:", route)
print("Приближённое расстояние:", distance)

Разбор кода

Функция nearest_neighbor_tsp(distance_matrix)
Инициализация:
visited = [False] * n – массив отслеживает, какие города уже посещены.
route = [0] – начинаем маршрут с первого города.
visited[0] = True – помечаем его как посещённый.

Основной цикл (for _ in range(n - 1)):
Находим ближайший непосещённый город:

nearest_city = min(
    [(i, distance_matrix[last_city][i]) for i in range(n) if not visited[i]],
    key=lambda x: x[1]
)[0]

Добавляем его в маршрут и помечаем как посещённый.

Завершение маршрута:

Возвращаемся в стартовый город route.append(0).
Вычисляем общее расстояние маршрута.

Возвращает:

route – полученный маршрут.
total_distance – длина маршрута.
Временная сложность: O(n^2), так как:

Каждую итерацию находим ближайший город (O(n))
Делаем n-1 итераций → O(n^2).

✅ Достоинства решения:

Быстрый алгоритм – работает за O(n^2), что намного лучше полного перебора O(n!) и ДП O(n^2 * 2^n).
Простая реализация.
Подходит для больших n (до 1000+).

❌ Недостатки решения:
- Не гарантирует оптимальный маршрут.
- Эффект жадности: может привести к "локальному минимуму", когда хороший выбор на ранних этапах приводит к плохому конечному решению.
- Зависит от стартового города: разные стартовые точки могут давать разные маршруты.

Методы ветвей и границ (Branch and Bound)#

Простой, но неэффективный метод — перебрать все возможные маршруты и выбрать оптимальный. Однако этот метод становится непрактичным при увеличении числа городов.

import heapq

def branch_and_bound_tsp(distance_matrix):
    n = len(distance_matrix)
    min_distance = float('inf')
    best_route = None
    def tsp(node, visited, cost, path):
        nonlocal min_distance, best_route
        if len(path) == n:
            cost += distance_matrix[node][0]
            if cost < min_distance:
                min_distance = cost
                best_route = path + [0]
            return
        for next_node in range(n):
            if next_node not in visited:
                tsp(next_node, visited | {next_node}, cost + distance_matrix[node][next_node], path + [next_node])
    tsp(0, {0}, 0, [0])
    return best_route, min_distance

Разбор кода

Функция branch_and_bound_tsp(distance_matrix)

Переменные:
- n = len(distance_matrix) – количество городов.
- min_distance = float('inf') – минимально найденное расстояние.
- best_route = None – лучший найденный маршрут.

Рекурсивная функция tsp(node, visited, cost, path):

Базовый случай:
- Если len(path) == n, значит обошли все города.
- Добавляем расстояние до стартового города: cost += distance_matrix[node][0].
- Если новый маршрут лучше найденного, обновляем min_distance и best_route.

Рекурсивный случай:
- Перебираем все возможные города next_node, которые ещё не посещены.
- Вызываем tsp() для следующего города с обновлённым cost и path.

Запуск алгоритма:

tsp(0, {0}, 0, [0])

Стартуем с нуля, посещён только первый город.

Возвращает:
- best_route – лучший найденный маршрут.
- min_distance – длина этого маршрута.

Временная сложность:
- В худшем случае: O(n!) (как полный перебор).
- В среднем случае: значительно быстрее, так как отсекает ненужные ветви.
- Использует нижнюю границу (bound), что сокращает количество перебираемых маршрутов.

Пространственная сложность:
- O(n) – из-за хранения visited и path.

✅ Достоинства решения:
- Находит оптимальное решение (если не прерывать алгоритм).
- Лучше, чем полный перебор (O(n!)), так как отсекает плохие маршруты.
- Не требует большого объёма памяти, как динамическое программирование (O(n * 2^n)) или ACO.

❌ Недостатки решения:
- Всё ещё экспоненциальная сложность в худшем случае.
- Может работать долго при n > 20, если не удаётся отсечь много ветвей.
- Зависит от порядка посещения городов – можно ускорить, если предварительно отсортировать рёбра.

Алгоритм Литтла или исключения подциклов#

Операция редукции по строкам
В каждой строке матрицы находят минимальный элемент d_min и вычитают его из всех элементов соответствующей строки.
Нижняя граница:
H = 3 * d_min
Операция редукции по столбцам
В каждом столбце матрицы выбирают минимальный элемент d_min и вычитают его из всех элементов соответствующего столбца.
Нижняя граница:
H = H + J * d_min
Константа приведения
Константа приведения H является нижней границей множества всех допустимых гамильтоновых контуров.
Поиск степеней нулей
Для приведенной по строкам и столбцам матрицы временно заменяют нули на знак «>» и находят сумму минимальных элементов строки и столбца, соответствующих этому нулю.
Выбор дуги с максимальной степенью нуля
Выбирают дугу (i, j), для которой степень нулевого элемента достигает максимального значения.
Разбиение множества на подмножества
Разбивают множество всех гамильтоновых контуров на два подмножества:
Подмножество контуров, содержащих дугу (i, j).
Подмножество контуров, не содержащих дугу (i, j).

Для получения матрицы контуров, включающих дугу (i, j), вычеркивают в матрице строку i и столбец j. Чтобы не допустить образования негамильтонова контура, заменяют симметричный элемент (j, i) на знак «>». Исключение дуги достигается заменой элемента в матрице на «∞».

Приведение матрицы контуров
Проводят приведение матрицы гамильтоновых контуров с поиском констант приведения H(i, j) и H(i*, j*).
Сравнение нижних границ подмножеств
Сравнивают нижние границы подмножества гамильтоновых контуров H(i, j) и H(i*, j*). Если:
H(i, j) < H(i*, j*), то дальнейшему ветвлению в первую очередь подлежит множество (i, j).
В противном случае разбиению подлежит множество (i*, j*).
Завершение ветвлений
Если в результате ветвлений получается матрица размером 2x2, то определяют полученный гамильтонов контур и его длину.
Сравнение длины гамильтонова контура с нижними границами
Сравнивают длину гамильтонова контура с нижними границами оборванных ветвей. Если длина контура не превышает их нижних границ, то задача решена.
В противном случае развивают ветви подмножеств с нижней границей, меньшей полученного контура, до тех пор, пока не получится маршрут с меньшей длиной.

Пример решения задачи коммивояжера методом ветвей и границ#

Решение будем вести с использованием калькулятора. Возьмем в качестве произвольного маршрута:

X0 = (1,2); (2,3); (3,4); (4,5); (5,1)

Тогда F(X0) = 90 + 40 + 60 + 50 + 20 = 260

Для определения нижней границы множества воспользуемся операцией редукции или приведения матрицы по строкам, для чего необходимо в каждой строке матрицы D найти минимальный элемент.

Матрица D:#

i/j	1	2	3	4	5	di
1	M	90	80	40	100	40
2	60	M	40	50	70	40
3	50	30	M	60	20	20
4	10	70	20	M	50	10
5	20	40	50	20	M	20

Затем вычитаем di из элементов рассматриваемой строки. В связи с этим во вновь полученной матрице в каждой строке будет как минимум один ноль.

Редуцированная матрица (по строкам):#

i/j	1	2	3	4	5
1	M	50	40	0	60
2	20	M	0	10	30
3	30	10	M	40	0
4	0	60	10	M	40
5	0	20	30	0	M

Теперь проводим редукцию по столбцам. Для этого в каждом столбце находим минимальный элемент.

Редуцированная матрица (по столбцам):#

i/j	1	2	3	4	5	dj
1	M	50	40	0	60	40
2	20	M	0	10	30	10
3	30	10	M	40	0	20
4	0	60	10	M	40	10
5	0	20	30	0	M	20

После вычитания минимальных элементов получаем полностью редуцированную матрицу:

Полностью редуцированная матрица:#

i/j	1	2	3	4	5
1	M	40	40	0	60
2	20	M	0	10	30
3	30	0	M	40	0
4	0	50	10	M	40
5	0	10	30	0	M

Сумма констант приведения определяет нижнюю границу H:

H = ∑di + ∑dj
H = 40 + 40 + 20 + 10 + 20 + 0 + 10 + 0 + 0 + 0 = 140

Элементы матрицы dij соответствуют расстоянию от пункта i до пункта j.

Поскольку в матрице n городов, то D является матрицей nxn с неотрицательными элементами dij >= 0.

Каждый допустимый маршрут представляет собой цикл, по которому коммивояжер посещает город только один раз и возвращается в исходный город. Длина маршрута определяется выражением:

F(Mk) = ∑dij

Причем каждая строка и столбец входят в маршрут только один раз с элементом dij.

Шаг 1

Определяем ребро ветвления и разбиваем все множество маршрутов относительно этого ребра на два подмножества (i,j) и (i*,j*).

С этой целью для всех клеток матрицы с нулевыми элементами заменяем поочередно нули на M (бесконечность) и определяем для них сумму образовавшихся констант приведения, они приведены в скобках.

Матрица с нулями, заменёнными на M:

i/j	1	2	3	4	5	di
1	M	40	40	0(40)	60	40
2	20	M	0(20)	10	30	10
3	30	0(10)	M	40	0(30)	0
4	0(10)	50	10	M	40	10
5	0(0)	10	30	0(0)	M	0

Шаг 2

Наибольшая сумма констант приведения равна (40 + 0) = 40 для ребра (1,4), следовательно, множество разбивается на два подмножества (1,4) и (1*,4*).

Нижняя граница гамильтоновых циклов этого подмножества:

H(1*,4*) = 140 + 40 = 180

Исключение ребра (1,4) проводим путем замены элемента d14 = 0 на M, после чего осуществляем очередное приведение матрицы расстояний для образовавшегося подмножества (1*,4*), в результате получим редуцированную матрицу.

Новая редуцированная матрица:

i/j	1	2	3	4	5	di
1	M	40	40	M	60	40
2	20	M	0	10	30	0
3	30	0	M	40	0	0
4	0	50	10	M	40	0
5	0	10	30	0	M	20

Итак, на каждом шаге происходит выбор оптимального ребра, исключение его из маршрута и пересчет нижней границы. Процесс продолжается до тех пор, пока не будут найдены все оптимальные ребра маршрута.

Результат:

Гамильтонов цикл образуют следующие ребра: (1,4), (4,3), (3,5), (5,2), (2,1). Длина маршрута равна:

F(Mk) = 180

Список источников#

Галяутдинов Р.Р. Задача коммивояжера — метод ветвей и границ // Сайт преподавателя экономики. [2023]. URL: https://galyautdinov.ru/post/zadacha-kommivoyazhera (дата обращения: 28.04.2025).

i/j	1	2	3	4	5	di
1	M	90	80	40	100	40
2	60	M	40	50	70	40
3	50	30	M	60	20	20
4	10	70	20	M	50	10
5	20	40	50	20	M	20

i/j	1	2	3	4	5	di
1	M	90	80	40	100	40
2	60	M	40	50	70	40
3	50	30	M	60	20	20
4	10	70	20	M	50	10
5	20	40	50	20	M	20

i/j	1	2	3	4	5	di
1	M	90	80	40	100	40
2	60	M	40	50	70	40
3	50	30	M	60	20	20
4	10	70	20	M	50	10
5	20	40	50	20	M	20