Задача поиска кратчайшего маршурта. Модификации алгоритма Дейсктры. Дельта-шаг. Алгоритм А*

Презентация Лекция 9

Параллелизация алгоритма Дейкстры[1]

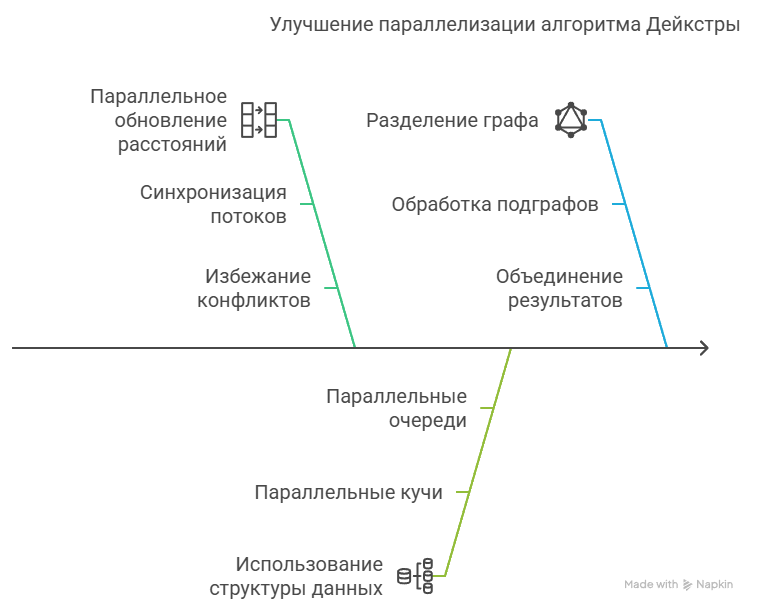
Рассмотрим алгоритм для направленного графа авторов Краузер, Мельхорн, Мейер, Сандерс, 1998 г.
Подход предполагает разделение графа на более мелкие подграфы и распараллеливание выполнения алгоритма Дейкстры на каждом подграфе с использованием подхода распараллеливания с общей памятью

Что подлежит параллелизации?

Основные компоненты алгоритма, которые можно распределить между процессами:

1. Обработка вершин
2. Распределение множества вершин V между процессами (V = V₁ ∪ V₂ ∪ ... ∪ Vₚ)

3. Локальные вычисления для "своих" вершин

4. Работа с очередями

5. Параллельное обслуживание трех типов очередей:

   • Q_d (основные расстояния)
   • Q_in (входящие ребра)
   • Q_out (исходящие ребра)

6. Обновление расстояний

7. Независимая обработка смежных вершин
8. Пакетное обновление значений

Инициализация

Для всех v ∈ Vᵢ положить:
d[v] = ∞
s — стартовая вершина
d[s] = 0
S = ∅

Добавить s в очереди Qᵈᵢ, Qᵢₙᵢ, Qₒᵤₜᵢ

---

Основной цикл

Пока хотя бы одна из очередей Qᵈᵢ не пуста:

1. На каждом процессе i:
2. Извлечь из Qₒᵤₜᵢ вершину с минимальным приоритетом → значение Lᵢ

3. Выполнить редукцию: L = min{ Lᵢ | i = 1, ..., P }

4. Аналогично:

5. Извлечь из Qᵈᵢ вершину с минимальным приоритетом → значение Mᵢ

6. Выполнить редукцию: M = min{ Mᵢ | i = 1, ..., P }

7. На каждом процессе:

8. Найти множество вершин Rᵢ, для которых d[v] ≤ L или in[v] ≤ M
9. Для этих вершин расстояние считается окончательно найденным

10. Обновить S: S = S ∪ ⋃Rᵢ

11. Удалить вершины из Rᵢ из очередей Qᵈᵢ, Qᵢₙᵢ, Qₒᵤₜᵢ

12. Сформировать множество пар (z, x), где:

13. z — необработанная вершина, смежная с вершинами из Rᵢ

14. x — вес ребра, ведущего к z

15. Для каждой пары (z, x) ∈ Zᵢ × Xᵢ:

16. Если d[z] > d[u] + x, то обновить: d[z] = d[u] + x

17. Обновить приоритеты вершины z в соответствующих очередях (своего или чужого процесса):
    Qᵈᵢ, Qᵢₙᵢ, Qₒᵤₜᵢ

18. Выполнить синхронизацию и проверить критерий останова

---

Реализация в коде

1. Установка количества потоков:

   • omp_set_num_threads(num_threads); — задает количество потоков для выполнения параллельных операций в OpenMP.

2. Инициализация данных:

   • Создаются вектора dist (для хранения расстояний) и visited (для отслеживания посещенных вершин).
   • Каждому потоку выделяется очередь с приоритетом (priority_queue), которая используется для обработки вершин графа.

3. Основной цикл обработки в параллельном блоке:

   • #pragma omp parallel — обозначает начало параллельного блока, в котором выполняются все потоки.
   • В каждом потоке идет извлечение вершины из очереди текущего потока с помощью local_queues[tid].top().
   • Если очередь текущего потока пуста, то происходит проверка очередей других потоков для нахождения работы.

4. Критическая секция для извлечения данных:

   • Для синхронизации доступа к общим данным используется #pragma omp critical, чтобы избежать одновременного доступа нескольких потоков к одной очереди.

5. Блокировка и синхронизация:

   • В случае, если работы нет, используется #pragma omp barrier для ожидания завершения работы всех потоков, после чего через #pragma omp single проверяется, есть ли еще задачи в других очередях.
   • Если все очереди пусты, выполнение завершается.

6. Обработка вершин:

   • Вершины, которые еще не были посещены, помечаются как "в процессе обработки".
   • Входные данные для обработки — это вершины графа и их соседи, которые добавляются в очереди для последующего обновления.

7. Обновление расстояний и добавление соседей в очереди:

   • Для каждого соседа проверяется, нужно ли обновить расстояние. Если расстояние обновляется, сосед добавляется в очередь соответствующего потока.

8. Завершение работы:

   • В конце каждого потока, после обработки всех вершин, посещенная вершина помечается как "обработанная" с помощью #pragma omp atomic write, что гарантирует корректное обновление данных в многопоточном окружении.

9. Измерение времени выполнения:

   • auto start = high_resolution_clock::now(); — начало измерения времени.
   • auto end = high_resolution_clock::now(); — завершение измерения времени.
   • Время выполнения измеряется в миллисекундах с использованием duration_cast<milliseconds>.

#include <iostream>
#include <vector>
#include <queue>
#include <limits>
#include <random>
#include <chrono>
#include <omp.h>
#include <fstream>
#include <algorithm>

using namespace std;
using namespace std::chrono;

struct QueueNode {
    int vertex;
    double distance;

    bool operator>(const QueueNode& other) const {
        return distance > other.distance;
    }
};

struct CRSGraph {
    vector<int> row_ptr;
    vector<int> col_ind;
    vector<double> weights;
    int n = 0;

    CRSGraph() = default;
    explicit CRSGraph(int size) : n(size) {}
};

CRSGraph generate_random_graph(int n, double density) {
    CRSGraph graph(n);
    graph.row_ptr.resize(n + 1);
    graph.row_ptr[0] = 0;

    random_device rd;
    mt19937 gen(rd());
    uniform_real_distribution<> weight_dist(1.0, 100.0);
    bernoulli_distribution edge_dist(density);

    for (int i = 0; i < n; ++i) {
        vector<int> cols;
        vector<double> wts;

        for (int j = 0; j < n; ++j) {
            if (i != j && edge_dist(gen)) {
                cols.push_back(j);
                wts.push_back(weight_dist(gen));
            }
        }

        graph.row_ptr[i + 1] = graph.row_ptr[i] + cols.size();
        graph.col_ind.insert(graph.col_ind.end(), cols.begin(), cols.end());
        graph.weights.insert(graph.weights.end(), wts.begin(), wts.end());
    }

    return graph;
}

double run_sequential_dijkstra(const CRSGraph& graph, int source) {
    const int n = graph.n;
    vector<double> dist(n, numeric_limits<double>::max());
    dist[source] = 0;

    priority_queue<QueueNode, vector<QueueNode>, greater<QueueNode>> pq;
    pq.push({ source, 0 });

    auto start = high_resolution_clock::now();

    while (!pq.empty()) {
        QueueNode node = pq.top();
        pq.pop();

        int u = node.vertex;
        if (node.distance > dist[u]) continue;

        for (int i = graph.row_ptr[u]; i < graph.row_ptr[u + 1]; ++i) {
            int v = graph.col_ind[i];
            double weight = graph.weights[i];

            if (dist[v] > dist[u] + weight) {
                dist[v] = dist[u] + weight;
                pq.push({ v, dist[v] });
            }
        }
    }

    auto end = high_resolution_clock::now();
    return duration_cast<milliseconds>(end - start).count();
}

double run_parallel_dijkstra(const CRSGraph& graph, int source, int num_threads) {
    omp_set_num_threads(num_threads);

    const int n = graph.n;
    vector<double> dist(n, numeric_limits<double>::max());
    vector<char> visited(n, 0);
    dist[source] = 0;

    int max_threads = num_threads;
    vector<priority_queue<QueueNode, vector<QueueNode>, greater<QueueNode>>> local_queues(max_threads);
    local_queues[0].push({ source, 0 });

    auto start = high_resolution_clock::now();

#pragma omp parallel
    {
        int tid = omp_get_thread_num();

        while (true) {
            QueueNode current;
            bool has_work = false;

            if (!local_queues[tid].empty()) {
#pragma omp critical
                {
                    if (!local_queues[tid].empty()) {
                        current = local_queues[tid].top();
                        local_queues[tid].pop();
                        has_work = true;
                    }
                }
            }

            if (!has_work) {
                for (int i = 0; i < max_threads; ++i) {
                    if (i == tid) continue;

#pragma omp critical
                    {
                        if (!local_queues[i].empty()) {
                            current = local_queues[i].top();
                            local_queues[i].pop();
                            has_work = true;
                        }
                    }
                    if (has_work) break;
                }
            }

            if (!has_work) {
#pragma omp barrier
#pragma omp single
                {
                    bool any_work = false;
                    for (auto& q : local_queues) {
                        if (!q.empty()) any_work = true;
                    }
                    if (!any_work) {
#pragma omp flush
                    }
                }
                break;
            }

            if (visited[current.vertex] == 2) continue;

            bool should_process = false;
#pragma omp critical
            {
                if (visited[current.vertex] == 0) {
                    visited[current.vertex] = 1;
                    should_process = true;
                }
            }

            if (!should_process) continue;

            int row_start = graph.row_ptr[current.vertex];
            int row_end = graph.row_ptr[current.vertex + 1];

            for (int i = row_start; i < row_end; ++i) {
                int neighbor = graph.col_ind[i];
                double weight = graph.weights[i];
                double new_dist = dist[current.vertex] + weight;

                bool updated = false;
#pragma omp critical
                {
                    if (new_dist < dist[neighbor]) {
                        dist[neighbor] = new_dist;
                        updated = true;
                    }
                }

                if (updated) {
                    int target_thread = neighbor % max_threads;
#pragma omp critical
                    {
                        local_queues[target_thread].push({ neighbor, dist[neighbor] });
                    }
                }
            }

#pragma omp atomic write
            visited[current.vertex] = 2;
        }
    }

    auto end = high_resolution_clock::now();
    return duration_cast<milliseconds>(end - start).count();
}

void run_benchmark_and_save_results() {
    vector<int> sizes = { 1000, 5000, 10000, 20000 };
    vector<double> densities = { 0.1, 0.3, 0.5 };
    vector<int> thread_counts = { 1, 2, 4, 8 };
    int repeats = 3;

    ofstream out("speedup_results.csv");
    out << "Size,Density,Threads,SeqTime(ms),ParTime(ms),Speedup\n";

    for (int size : sizes) {
        for (double density : densities) {
            // Генерация графа
            auto gen_start = high_resolution_clock::now();
            CRSGraph graph = generate_random_graph(size, density);
            auto gen_end = high_resolution_clock::now();
            cout << "Generated graph: size=" << size << ", density=" << density
                << " in " << duration_cast<milliseconds>(gen_end - gen_start).count() << " ms\n";

            // Выбор исходной вершины
            int source = 0;
            while (graph.row_ptr[source + 1] - graph.row_ptr[source] == 0) {
                source = (source + 1) % size;
            }

            // Последовательная версия
            double seq_time = 0;
            for (int i = 0; i < repeats; ++i) {
                seq_time += run_sequential_dijkstra(graph, source);
            }
            seq_time /= repeats;

            // Параллельные версии
            for (int threads : thread_counts) {
                double par_time = 0;
                for (int i = 0; i < repeats; ++i) {
                    par_time += run_parallel_dijkstra(graph, source, threads);
                }
                par_time /= repeats;

                double speedup = seq_time / par_time;
                out << size << "," << density << "," << threads << ","
                    << seq_time << "," << par_time << "," << speedup << "\n";
                cout << "Size: " << size << ", Density: " << density
                    << ", Threads: " << threads << ", Speedup: " << speedup << "\n";
            }
        }
    }
    out.close();
}

int main() {
    run_benchmark_and_save_results();
    cout << "Benchmark completed. Results saved to speedup_results.csv\n";

    return 0;
}

Алгоритм дельта-шага

Note

Алгоритм дельта-шаган предназначен для решения задачи поиска кратчайшего пути на графе. Для заданного ориентированного взвешенного графа с неотрицательными весами алгоритм находит кратчайшие расстояния от выделенной вершины-источника до всех остальных вершин графа. Алгоритм изначально проектировался с целью эффективной параллелизации.

Идея: модифицировать алгоритм Дейкстры, сгруппировав вершины с близкими значениями расстояний, чтобы пересчитывать их одновременно.

• Вводится параметр Δ > 0 для разделения рёбер:
• Лёгкие: вес < Δ
• Тяжёлые: вес ≥ Δ
• Вершины группируются в "карманы" (buckets) по текущей оценке расстояния:
• 𝐵[𝑖] содержит вершины с 𝑑[𝑣] ∈ [𝑖Δ, (𝑖+1)Δ)

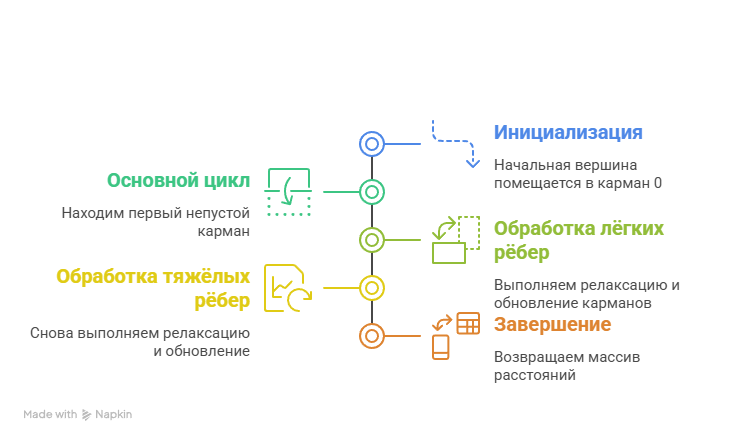
Псевдокод алгоритма

1. Предобработка:

2. Для каждой вершины 𝑣:

   • 𝐿[𝑣] ← все рёбра с весом < Δ
   • 𝐻[𝑣] ← все рёбра с весом ≥ Δ

3. Инициализация:

4. ∀𝑣 ∈ 𝑉: 𝑑[𝑣] ← ∞
5. 𝑑[𝑠] ← 0
6. 𝐵[0] ← {𝑠}

7. 𝑖 ← 0

8. Основной цикл (пока ∃ непустые карманы):

9. 𝑆 ← ∅
10. Пока 𝐵[𝑖] ≠ ∅:
    • Req ← {(𝑢, 𝑥) | 𝑣 ∈ 𝐵[𝑖], (𝑣,𝑢) ∈ 𝐿[𝑣], 𝑥 = 𝑑[𝑣] + 𝑤(𝑣,𝑢)}
    • 𝑆 ← 𝑆 ∪ 𝐵[𝑖]
    • 𝐵[𝑖] ← ∅
    • Для каждого (𝑢, 𝑥) ∈ Req:
    • Если 𝑑[𝑢] > 𝑥:
      • Удалить 𝑢 из 𝐵[⌊𝑑[𝑢]/Δ⌋]
      • 𝑑[𝑢] ← 𝑥
      • Добавить 𝑢 в 𝐵[⌊𝑥/Δ⌋]
11. Req ← {(𝑢, 𝑥) | 𝑣 ∈ 𝑆, (𝑣,𝑢) ∈ 𝐻[𝑣], 𝑥 = 𝑑[𝑣] + 𝑤(𝑣,𝑢)}
12. Для каждого (𝑢, 𝑥) ∈ Req:
    • Если 𝑑[𝑢] > 𝑥:
    • Удалить 𝑢 из 𝐵[⌊𝑑[𝑢]/Δ⌋]
    • 𝑑[𝑢] ← 𝑥
    • Добавить 𝑢 в 𝐵[⌊𝑥/Δ⌋]

Или более алгоритмически:

Входные данные:
  граф с вершинами V, рёбрами E с весами W;
  вершина-источник u;
  параметр Δ > 0.
Выходные данные: расстояния d(v) до каждой вершины v ∈ V от вершины u.

procedure DeltaStepping(V, E, W, u, Δ):
     LightEdges := { e ∈ E | W(e) ≤ Δ }
     HeavyEdges := { e ∈ E | W(e) > Δ }
     for each v ∈ V do d(v) := ∞
     Relax(u, 0)
     while any({ Buckets(i) ≠ ∅ }):
         Bucket := first({ Buckets(i) ≠ ∅ })
         Deleted := ∅
         while Bucket ≠ ∅:
             Requests := FindRequests(Bucket, LightEdges)
             Deleted := Deleted ∪ Bucket
             Bucket := ∅
             RelaxAll(Requests)
         RelaxAll(FindRequests(Deleted, HeavyEdges))

procedure Relax(v, x):
    if x < d(v):
        OldBucket := B(⌊d(v) / Δ⌋)
        NewBucket := B(⌊x / Δ⌋)
        OldBucket := OldBucket \ {v}
        NewBucket := NewBucket ∪ {v}
        d(v) := x

procedure RelaxAll(R):
    for each (v, x) ∈ R do Relax(v, x)

function FindRequests(V', E'):
    return { (w, d(w) + W(v, w)) | v ∈ V' and (v, w) ∈ E'}

Анализ сложности

Для случайных графов с весами ∈ [0,1] и Δ = Θ(1/𝑚):

Среднее время работы = O(n + m + dL)

где:
- 𝑑 — максимальная степень вершины
- 𝐿 — длина максимального кратчайшего пути

Особенности реализации

1. Структуры данных:
2. Карманы: динамические массивы с O(1) на вставку/удаление

3. Множество Req:

   • Основной массив пар (𝑢, 𝑥)
   • Массив меток для проверки принадлежности

4. Выбор Δ:

5. Оптимально: Δ ≈ среднему весу рёбер
6. Крайние случаи:
   • Δ → ∞ → Дейкстра
   • Δ → 0 → Bellman-Ford

Пример работы алгоритм дельта-шага

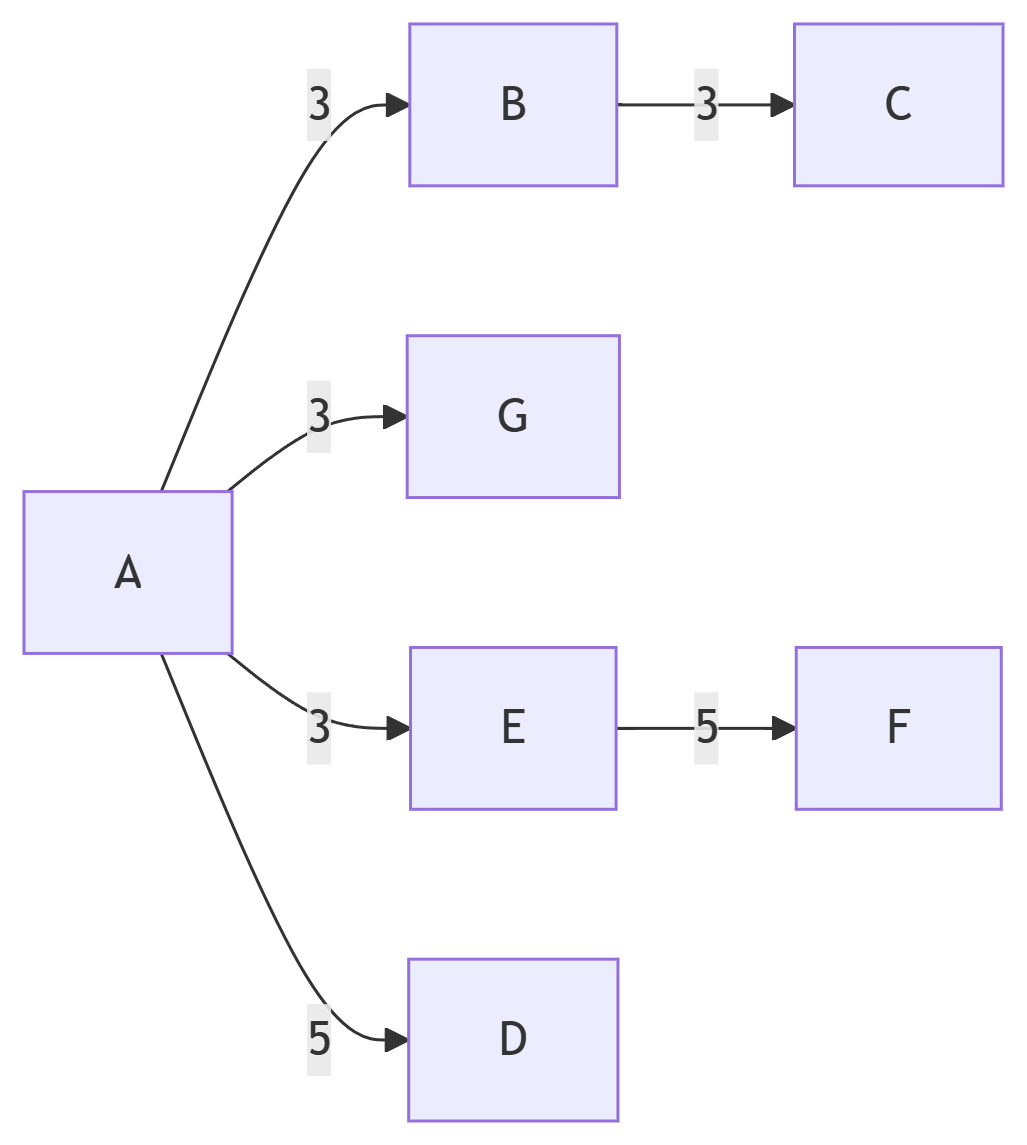
Пошаговая демонстрация работы алгоритма Δ-Шага

Рассмотрим выполнение алгоритма на небольшом графе. Вершина-источник — A, параметр Δ = 3.

В начале алгоритма все вершины, кроме источника, имеют бесконечные оценки расстояний:

Вершина	A	B	C	D	E	F	G
Расстояние	0	∞	∞	∞	∞	∞	∞

Карманы:

• B[0] охватывает диапазон [0, 2]
• B[1] охватывает диапазон [3, 5]
• B[2] охватывает диапазон [6, 8]

Начальное состояние:
- B[0] = {A}
- Остальные карманы пусты

---

Шаг 1. Обработка легких ребер из B[0]

Обрабатываются легкие ребра, инцидентные вершине A:
- A — B, A — G, A — E

Результат:
- B, G, E помещаются в B[1]

Поскольку B[0] опустел, обрабатывается тяжелое ребро:
- A — D

Новые расстояния:

Вершина	A	B	C	D	E	F	G
Расстояние	0	3	∞	5	3	∞	3

---

Шаг 2. Обработка легких ребер из B[1]

Обрабатываются легкие ребра от B, E, G:
- G — C

Результат:
- C добавляется в B[2]

Поскольку B[1] опустел, обрабатывается тяжелое ребро:
- E — F

Обновленные расстояния:

Вершина	A	B	C	D	E	F	G
Расстояние	0	3	6	5	3	8	3

---

Шаг 3. Обработка кармана B[2]

Обработка B[2] не приводит к улучшению расстояний.

---

Завершение

Алгоритм завершает работу, так как все карманы пусты.

Преимущества и недостатки

Преимущества	Недостатки
Эффективен для разреженных графов	Зависит от выбора Δ
Возможность параллелизации	Доп. расходы на управление карманами
Уменьшает число операций с очередью	Сложность реализации структур

Примечание: За счет разбиения на легкие и тяжелые ребра по карманам возможна параллелизация

Реализация последовательного дельта-шага

#include <iostream>
#include <vector>
#include <queue>
#include <limits>
#include <cmath>
#include <unordered_map>
#include <unordered_set>

using namespace std;

const int INF = numeric_limits<int>::max();

class DeltaStepping {
    struct Edge {
        int to;
        int weight;
    };

    int delta;
    vector<vector<Edge>> light_edges;
    vector<vector<Edge>> heavy_edges;
    vector<int> dist;
    vector<unordered_set<int>> buckets;
    int max_bucket;

public:
    DeltaStepping(const vector<vector<pair<int, int>>>& graph, int delta) 
        : delta(delta) {
        int n = graph.size();
        light_edges.resize(n);
        heavy_edges.resize(n);
        dist.assign(n, INF);

        // Предобработка: разделяем ребра на легкие и тяжелые
        for (int u = 0; u < n; ++u) {
            for (const auto& [v, w] : graph[u]) {
                if (w <= delta) {
                    light_edges[u].push_back({v, w});
                } else {
                    heavy_edges[u].push_back({v, w});
                }
            }
        }

        // Инициализация карманов
        max_bucket = 0;
        buckets.resize(1);
    }

    void relax(int v, int x, unordered_set<int>& new_bucket) {
        if (x < dist[v]) {
            // Удаляем из старого кармана (если был там)
            if (dist[v] != INF) {
                int old_bucket = dist[v] / delta;
                if (old_bucket < buckets.size()) {
                    buckets[old_bucket].erase(v);
                }
            }

            // Обновляем расстояние
            dist[v] = x;

            // Добавляем в новый карман
            int new_bucket_idx = x / delta;

            // Увеличиваем количество карманов при необходимости
            if (new_bucket_idx >= buckets.size()) {
                buckets.resize(new_bucket_idx + 1);
                max_bucket = new_bucket_idx;
            }

            // Помечаем для добавления
            new_bucket.insert(v);
        }
    }

    vector<int> shortest_path(int source) {
        dist[source] = 0;
        buckets[0].insert(source);

        while (true) {
            // Находим первый непустой карман
            int current_bucket = -1;
            for (int i = 0; i <= max_bucket; ++i) {
                if (!buckets[i].empty()) {
                    current_bucket = i;
                    break;
                }
            }

            if (current_bucket == -1) break;

            unordered_set<int> new_bucket;
            unordered_set<int> S;

            // Обрабатываем легкие ребра
            while (!buckets[current_bucket].empty()) {
                unordered_set<int> current_vertices = move(buckets[current_bucket]);
                S.insert(current_vertices.begin(), current_vertices.end());

                // Релаксация легких ребер
                for (int v : current_vertices) {
                    for (const Edge& e : light_edges[v]) {
                        relax(e.to, dist[v] + e.weight, new_bucket);
                    }
                }
            }

            // Добавляем вершины в карман
            for (int v : new_bucket) {
                buckets[dist[v] / delta].insert(v);
            }
            new_bucket.clear();

            // Обрабатываем тяжелые ребра
            for (int v : S) {
                for (const Edge& e : heavy_edges[v]) {
                    relax(e.to, dist[v] + e.weight, new_bucket);
                }
            }

            // Добавляем вершины после обработки тяжелых ребер
            for (int v : new_bucket) {
                buckets[dist[v] / delta].insert(v);
            }
        }

        return dist;
    }
};

int main() {
    // Пример графа: список смежности {вершина, вес}
    vector<vector<pair<int, int>>> graph = {
        {{1, 2}, {2, 6}},       // 0
        {{2, 3}, {3, 5}},        // 1
        {{3, 2}, {4, 4}},        // 2
        {{4, 1}},                // 3
        {}                       // 4
    };

    int delta = 3; // Выбираем порог delta
    DeltaStepping ds(graph, delta);

    int source = 0;
    vector<int> distances = ds.shortest_path(source);

    cout << "Кратчайшие расстояния от вершины " << source << ":\n";
    for (int i = 0; i < distances.size(); ++i) {
        cout << "До " << i << ": " << distances[i] << endl;
    }

    return 0;
}

Параллельный алгоритм дельта-шага

Синхронизация: потоки (процессы) обмениваются подмножествами $\text{Req}$, чтобы каждый обрабатывал запросы только для своих локальных вершин. Дубли удаляются при формировании $\text{Req}$.
Дополнительно синхронизируются:
- переход к следующему непустому карману,
- проверка критерия останова.

Предобработка (в параллель): для всех $v \in V$ сформировать списки $L[v]$ и $H[v]$

Инициализация (в параллель): для всех $v \in V$: $d[v] = \infty$, $B[0] = \{s\}$

Основной цикл:

1. На каждом потоке $k$: $S[k] = ∅$
2. Пока карман $B[i]$ не пуст:
3. Параллельно: для локальных вершин из $B[i]$ построить $\text{Req}[k]$ без дублей
4. $S[k] = S[k] ∪ B[i]$, $B[i] = ∅$
5. Обменяться $\text{Req}[k]$, выполнить релаксацию локально
6. Параллельно: построить $\text{Req}[k]$ из рёбер $H[v]$, где $v \in S[k]$
7. Обменяться $\text{Req}[k]$, выполнить релаксацию
8. Синхронизация: найти следующий непустой карман

Пример тестирования кода:

#include <iostream>
#include <vector>
#include <queue>
#include <limits>
#include <algorithm>
#include <set>
#include <memory>
#include <cmath>
#include <omp.h>
#include <random>
#include <chrono>

using namespace std;

const int INF = numeric_limits<int>::max();

// Graph class for Dijkstra's implementation
class Graph {
    int V;
    vector<vector<pair<int, int>>> adj;

public:
    Graph(int V) : V(V), adj(V) {}

    void addEdge(int u, int v, int w) {
        adj[u].push_back({ v, w });
        adj[v].push_back({ u, w });
    }

    void dijkstra(int src) {
        priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
        vector<int> dist(V, INF);

        pq.push({ 0, src });
        dist[src] = 0;

        while (!pq.empty()) {
            int u = pq.top().second;
            pq.pop();

            for (auto& edge : adj[u]) {
                int v = edge.first;
                int weight = edge.second;

                if (dist[v] > dist[u] + weight) {
                    dist[v] = dist[u] + weight;
                    pq.push({ dist[v], v });
                }
            }
        }

        // Commented out to reduce output clutter during measurements
        // cout << "Dijkstra Results:\nVertex\tDistance\n";
        // for (int i = 0; i < V; ++i)
        //     cout << i << "\t" << dist[i] << "\n";
    }
};

// Delta-Stepping implementation
void relax(int u, int v, int weight, vector<int>& distances, int delta, vector<set<int>>& buckets) {
    int old_distance = distances[v];
    int new_distance = distances[u] + weight;
    if (new_distance < old_distance) {
        distances[v] = new_distance;
        int old_bucket = old_distance / delta;
        int new_bucket = new_distance / delta;
        if (old_distance != INF) {
            buckets[old_bucket].erase(v);
        }
        buckets[new_bucket].insert(v);
    }
}

void delta_stepping(int source, const vector<vector<pair<int, int>>>& graph, vector<int>& distances, int delta) {
    int n = graph.size();
    distances.assign(n, INF);
    distances[source] = 0;

    int max_buckets = 3 * n;
    vector<set<int>> buckets(max_buckets);
    buckets[0].insert(source);

    for (int i = 0; i < max_buckets; ++i) {
        while (!buckets[i].empty()) {
            set<int> S = buckets[i];
            buckets[i].clear();

            // Light edges
#pragma omp parallel for schedule(dynamic)
            for (int u : S) {
                for (const auto& edge : graph[u]) {
                    if (edge.second <= delta) {
#pragma omp critical
                        relax(u, edge.first, edge.second, distances, delta, buckets);
                    }
                }
            }

            // Heavy edges
#pragma omp parallel for schedule(dynamic)
            for (int u : S) {
                for (const auto& edge : graph[u]) {
                    if (edge.second > delta) {
#pragma omp critical
                        relax(u, edge.first, edge.second, distances, delta, buckets);
                    }
                }
            }
        }
    }
}

// Function to generate a random graph with given size and density
vector<vector<pair<int, int>>> generateRandomGraph(int size, double density) {
    vector<vector<pair<int, int>>> graph(size);
    random_device rd;
    mt19937 gen(rd());
    uniform_int_distribution<> weight_dist(1, 100);
    uniform_real_distribution<> prob_dist(0.0, 1.0);

    for (int u = 0; u < size; ++u) {
        for (int v = u + 1; v < size; ++v) {
            if (prob_dist(gen) < density) {
                int weight = weight_dist(gen);
                graph[u].push_back({ v, weight });
                graph[v].push_back({ u, weight });
            }
        }
    }

    // Ensure the graph is connected by adding at least one edge per vertex
    for (int u = 0; u < size; ++u) {
        if (graph[u].empty()) {
            int v = (u + 1) % size;
            int weight = weight_dist(gen);
            graph[u].push_back({ v, weight });
            graph[v].push_back({ u, weight });
        }
    }

    return graph;
}

void runComparison(int n, double density) {
    cout << "\n=== Comparing algorithms for n = " << n << ", density = " << density << " ===\n";

    // Generate random graph
    auto adjList = generateRandomGraph(n, density);

    // Create Graph object for Dijkstra
    Graph g(n);
    for (int u = 0; u < adjList.size(); u++) {
        for (const auto& edge : adjList[u]) {
            if (u < edge.first) { // Avoid adding edges twice
                g.addEdge(u, edge.first, edge.second);
            }
        }
    }

    // Run Dijkstra's algorithm
    double start = omp_get_wtime();
    g.dijkstra(0);
    double dijkstra_time = omp_get_wtime() - start;
    printf("Dijkstra's time: %f seconds\n", dijkstra_time);

    // Run Delta-Stepping algorithm
    vector<int> distances;
    int delta = 10; // Fixed delta value for simplicity
    start = omp_get_wtime();
    delta_stepping(0, adjList, distances, delta);
    double delta_time = omp_get_wtime() - start;

    // Commented out to reduce output clutter during measurements
    // cout << "Delta-Stepping Results:\nVertex\tDistance\n";
    // for (int i = 0; i < distances.size(); ++i)
    //     cout << i << "\t" << distances[i] << "\n";
    printf("Delta-Stepping time: %f seconds\n", delta_time);

    cout << "\nSpeedup: " << dijkstra_time / delta_time << "x\n";
}

int main() {
    omp_set_num_threads(4); // Use 4 threads for parallel sections

    // Test parameters
    vector<int> sizes = { 10000, 20000, 30000, 50000 };
    vector<double> densities = { 0.1, 0.3, 0.5, 0.7, 0.9 };

    // Run comparisons for all combinations
    for (int n : sizes) {
        for (double d : densities) {
            runComparison(n, d);
        }
    }

    return 0;
}

Алгоритм А зведочка

Алгоритм A* является одним из наиболее популярных и эффективных алгоритмов поиска пути, используемых в различных областях, таких как робототехника, игры и навигационные системы. Он сочетает в себе преимущества алгоритмов поиска по ширине и жадного поиска, что позволяет ему находить оптимальные решения с минимальными затратами времени и ресурсов.

A* — это модификация алгоритма Дейкстры, оптимизированная для единственной конечной точки. Алгоритм Дейкстры может находить пути ко всем точкам, A* находит путь к одной точке. Он отдаёт приоритет путям, которые ведут ближе к цели.

A* пошагово просматривает все пути, ведущие от начальной вершины в конечную, пока не найдёт минимальный. Как и все информированные алгоритмы поиска, он просматривает сначала те маршруты, которые «кажутся» ведущими к цели. Он использует эвристическую функцию, которая помогает выбрать наиболее перспективное направление поиска.

• g(n) — стоимость пути от начальной вершины до вершины n.
• h(n) — эвристическая оценка расстояния от n до цели.
• f(n) = g(n) + h(n) — общая оценка стоимости пути через вершину n.

Алгоритм выбирает вершины с наименьшим значением f(n).

A*(start, goal):
    openSet ← {start}
    gScore[start] ← 0
    fScore[start] ← h(start)

    while openSet is not empty:
        current ← вершина в openSet с наименьшим fScore[current]
        if current == goal:
            return восстановить путь

        openSet.remove(current)
        for каждый сосед neighbor of current:
            tentative_gScore ← gScore[current] + расстояние(current, neighbor)
            if tentative_gScore < gScore[neighbor]:
                cameFrom[neighbor] ← current
                gScore[neighbor] ← tentative_gScore
                fScore[neighbor] ← gScore[neighbor] + h(neighbor)
                if neighbor not in openSet:
                    openSet.add(neighbor)

    return "Путь не найден"

Список источников

1. А А. Аль-саиди, И О. Темкин, В И. Алтай, А Ф. Алмунтафеки, А Н. Мохедхуссин Повышение эффективности алгоритма Дейкстры с помощью технологий параллельных вычислений с библиотекой OpenMP // ИВД. 2023. №8 (104). URL: https://cyberleninka.ru/article/n/povyshenie-effektivnosti-algoritma-deykstry-s-pomoschyu-tehnologiy-parallelnyh-vychisleniy-s-bibliotekoy-openmp (дата обращения: 21.04.2025).