Парраллелизм графовых задач. Задача поиска кратчайшего маршурта#
Почему навыки параллельного программирования станут актуальнее?#
В марте 2025 года на конференции GTC компания NVIDIA объявила о внедрении нативной поддержки языка Python в программную платформу CUDA. Это событие можно рассматривать как важный поворотный момент в развитии высокопроизводительных вычислений, поскольку оно знаменует собой переход от узкоспециализированного и труднодоступного GPU-программирования к более демократичному и широкодоступному формату, ориентированному на сообщество разработчиков, использующих Python.
До настоящего времени программирование под CUDA требовало глубокого знания языка C++ и особенностей архитектуры GPU. Теперь, благодаря интеграции Python, становится возможной разработка параллельных алгоритмов, включая графовые, средствами высокоуровневого синтаксиса, привычного для специалистов в области анализа данных, машинного обучения и научных вычислений.
Вместо ручного управления потоками, как в C++, NVIDIA предлагает модель CuTile, которая оперирует массивами, а не отдельными элементами. Это упрощает отладку и делает код читаемым, не жертвуя скоростью. По сути, разработчики получают высокоуровневую абстракцию, скрывающую сложности железа, но сохраняющую гибкость.
Пока (CuTile)[https://pypi.org/project/cutile-python/] доступен только для Python, но в планах — расширение для C++. Это часть стратегии NVIDIA по поддержке новых языков: Rust и Julia уже на походе.
Графовые задачи и потенциал распараллеливания#
Значительная часть задач на графах обладает высокой степенью параллелизма. В частности, к ним относятся:
- Поиск кратчайших путей (алгоритмы Dijkstra, Delta-Stepping);
- Поиск компонент связности;
- Вычисление центральности, PageRank и другие задачи сетевого анализа.
Современные реализации таких алгоритмов с использованием GPU позволяют добиться значительного ускорения по сравнению с классическим подходом на CPU, особенно при работе с крупными графами.
Формат хранения матрицы Compressed Row Storage, CRS#
CRS использует три массива:
weights— значения ненулевых элементов (весов ребер).adjncy— номера столбцов, соответствующих значениям изweights.xadj— индексы начала каждой строки (вершины) в массивахweightsиadjncy.
Пусть задан граф с 4 вершинами и следующей матрицей смежности (весовой):
0 1 2 3
+------------
0 | 0 5 0 0
1 | 0 0 3 0
2 | 0 0 0 1
3 | 2 0 0 0
Сначала сформируем списки смежности по строкам матрицы:
- Вершина 0 → 1 (вес 5)
- Вершина 1 → 2 (вес 3)
- Вершина 2 → 3 (вес 1)
- Вершина 3 → 0 (вес 2)
Запишем все ребра последовательно в adjnc. Чтобы ориентироваться, какой элемент нашего списка относится к какой вершине, заведём отдельный массив с указателями на начало подсписков — xadjr.
Теперь сформируем три массива CRS:
-
weights = [5, 3, 1, 2]
(веса ребер, считанные по строкам: 0→1, 1→2, 2→3, 3→0) -
adjncy = [1, 2, 3, 0]
(столбцы, в которых находятся ненулевые значения) -
xadj = [0, 1, 2, 3, 4]
(индексы начала каждой строки вvaluesиadjncy: - строка 0 — элементы с индекса 0 до 1,
- строка 1 — элементы с индекса 1 до 2,
- строка 2 — элементы с индекса 2 до 3,
- строка 3 — элементы с индекса 3 до 4)
Иллюстрация для другого графа
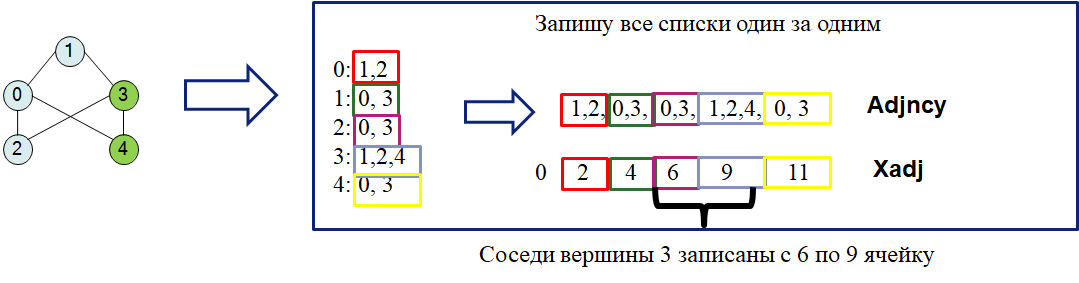
Реализация CRS#
Формат CRS удобен не только для компактного хранения, но и для распараллеливания вычислений. Все данные (веса и смежные вершины) хранятся в линейных массивах weights и adjncy, а доступ к подспискам обеспечивается через xadj. Это позволяет эффективно распределять работу между потоками или процессами, не дублируя данные.
Поскольку при обработке графа каждый процесс может обрабатывать только свою подгруппу вершин, достаточно знать, какие строки CRS относятся к какому процессу. Для этого вводится дополнительный массив:
vertex_dist— массив размера(P + 1), гдеP— число процессов.
Элементvertex_dist[i]указывает на глобальный индекс вершины, с которой начинается диапазон, обрабатываемый процессомi.
Таким образом, процессiобрабатывает вершины отvertex_dist[i]доvertex_dist[i+1] - 1.
Если в системе 3 процесса (P = 3) и 6 вершин, можно распределить их так:
vertex_dist = [0, 2, 4, 6]
- Процесс 0 обрабатывает вершины 0 и 1
- Процесс 1 — вершины 2 и 3
- Процесс 2 — вершины 4 и 5
Каждый процесс хранит только свой диапазон строк массива xadj, и соответствующие элементы из weights и adjncy. Это удобно для распределённых алгоритмов поиска путей, вычисления степени центральности и других задач на графах.
Такой подход минимизирует пересылку данных и повышает эффективность параллельной обработки.
import numpy as np
class CRSGraph:
def __init__(self, vertex_dist, adjncy, xadj, eweights=None):
"""
Инициализация графа в формате CRS
Параметры:
vertex_dist - массив распределения вершин между процессами (P+1 элементов)
adjncy - массив смежных вершин (2*M элементов)
xadj - массив индексов начала списков смежности (N+1 элементов)
eweights - (опционально) массив весов ребер (2*M элементов)
"""
self.vertex_dist = np.array(vertex_dist, dtype=np.int32)
self.adjncy = np.array(adjncy, dtype=np.int32)
self.xadj = np.array(xadj, dtype=np.int32)
self.eweights = np.array(eweights, dtype=np.float32) if eweights is not None else None
self.num_processes = len(vertex_dist) - 1
self.num_vertices = len(xadj) - 1
self.num_edges = len(adjncy) // 2
def get_local_vertices(self, process_id):
"""Возвращает диапазон вершин для указанного процесса"""
if process_id < 0 or process_id >= self.num_processes:
raise ValueError("Неверный ID процесса")
return range(self.vertex_dist[process_id], self.vertex_dist[process_id + 1])
def get_adjacent_vertices(self, vertex):
"""Возвращает смежные вершины для указанной вершины"""
if vertex < 0 or vertex >= self.num_vertices:
raise ValueError("Неверный ID вершины")
start_idx = self.xadj[vertex]
end_idx = self.xadj[vertex + 1]
return self.adjncy[start_idx:end_idx]
def get_edge_weights(self, vertex):
"""Возвращает веса ребер для указанной вершины (если есть)"""
if self.eweights is None:
return None
if vertex < 0 or vertex >= self.num_vertices:
raise ValueError("Неверный ID вершины")
start_idx = self.xadj[vertex]
end_idx = self.xadj[vertex + 1]
return self.eweights[start_idx:end_idx]
def memory_usage(self):
"""Возвращает оценку использования памяти в байтах"""
mem = 4 * (len(self.adjncy)) * 2 # adjncy (int32) и eweights (float32)
mem += 4 * len(self.xadj) # xadj (int32)
mem += 4 * len(self.vertex_dist) # vertex_dist (int32)
return mem
@staticmethod
def from_edge_list(vertex_dist, edge_list, weighted=False):
"""
Создает граф в формате CRS из списка ребер
Параметры:
vertex_dist - распределение вершин между процессами
edge_list - список ребер в формате [(u1, v1, w1), ...] или [(u1, v1), ...]
weighted - флаг, указывающий на наличие весов
"""
num_vertices = vertex_dist[-1]
num_edges = len(edge_list)
# Сортируем ребра по исходным вершинам
edge_list_sorted = sorted(edge_list, key=lambda x: x[0])
# Инициализация массивов
xadj = np.zeros(num_vertices + 1, dtype=np.int32)
adjncy = np.zeros(2 * num_edges, dtype=np.int32)
eweights = np.zeros(2 * num_edges, dtype=np.float32) if weighted else None
# Заполняем xadj и adjncy
current_vertex = 0
xadj[0] = 0
edge_idx = 0
for u, v, *rest in edge_list_sorted:
# Добавляем прямое ребро
adjncy[edge_idx] = v
if weighted:
eweights[edge_idx] = rest[0]
edge_idx += 1
# Добавляем обратное ребро (если граф неориентированный)
adjncy[edge_idx] = u
if weighted:
eweights[edge_idx] = rest[0]
edge_idx += 1
# Обновляем xadj для вершин, которые мы пропустили
while current_vertex < u:
current_vertex += 1
xadj[current_vertex] = edge_idx - 1
# Заполняем xadj для оставшихся вершин
for v in range(current_vertex + 1, num_vertices + 1):
xadj[v] = edge_idx
return CRSGraph(vertex_dist, adjncy, xadj, eweights)
Пример использования
vertex_dist = [0, 2, 4] # 2 процесса: 0-1 на процессе 0, 2-3 на процессе 1
edge_list = [(0, 1, 5), (1, 2, 3), (2, 3, 2)] # (u, v, weight)
# Создаем граф
graph = CRSGraph.from_edge_list(vertex_dist, edge_list, weighted=True)
# Получаем смежные вершины для вершины 1
print("Смежные с вершиной 1:", graph.get_adjacent_vertices(1))
print("Веса ребер для вершины 1:", graph.get_edge_weights(1))
# Получаем вершины для процесса 0
print("Вершины процесса 0:", list(graph.get_local_vertices(0)))
# Использование памяти
print("Использование памяти (байт):", graph.memory_usage())
#include <iostream>
#include <vector>
#include <algorithm>
#include <stdexcept>
#include <numeric>
class CRSGraph {
private:
std::vector<int> vertex_dist;
std::vector<int> adjncy;
std::vector<int> xadj;
std::vector<float> eweights;
int num_processes;
int num_vertices;
int num_edges;
bool weighted;
public:
// Конструктор
CRSGraph(const std::vector<int>& vertex_dist,
const std::vector<int>& adjncy,
const std::vector<int>& xadj,
const std::vector<float>& eweights = {})
: vertex_dist(vertex_dist), adjncy(adjncy), xadj(xadj), eweights(eweights) {
this->num_processes = vertex_dist.size() - 1;
this->num_vertices = xadj.size() - 1;
this->num_edges = adjncy.size() / 2;
this->weighted = !eweights.empty();
}
// Получить локальные вершины для процесса
std::pair<int, int> get_local_vertices(int process_id) const {
if (process_id < 0 || process_id >= num_processes) {
throw std::out_of_range("Invalid process ID");
}
return { vertex_dist[process_id], vertex_dist[process_id + 1] };
}
// Получить смежные вершины
std::vector<int> get_adjacent_vertices(int vertex) const {
if (vertex < 0 || vertex >= num_vertices) {
throw std::out_of_range("Invalid vertex ID");
}
int start_idx = xadj[vertex];
int end_idx = xadj[vertex + 1];
return std::vector<int>(adjncy.begin() + start_idx, adjncy.begin() + end_idx);
}
// Получить веса ребер
std::vector<float> get_edge_weights(int vertex) const {
if (!weighted) {
return {};
}
if (vertex < 0 || vertex >= num_vertices) {
throw std::out_of_range("Invalid vertex ID");
}
int start_idx = xadj[vertex];
int end_idx = xadj[vertex + 1];
return std::vector<float>(eweights.begin() + start_idx, eweights.begin() + end_idx);
}
// Оценка использования памяти
size_t memory_usage() const {
size_t mem = adjncy.size() * sizeof(int); // adjncy
mem += eweights.size() * sizeof(float); // eweights
mem += xadj.size() * sizeof(int); // xadj
mem += vertex_dist.size() * sizeof(int); // vertex_dist
return mem;
}
// Создание графа из списка ребер
static CRSGraph from_edge_list(const std::vector<int>& vertex_dist,
const std::vector<std::tuple<int, int, float>>& edge_list,
bool weighted = false) {
int num_vertices = vertex_dist.back();
int num_edges = edge_list.size();
// Сортируем ребра по исходным вершинам
std::vector<std::tuple<int, int, float>> edge_list_sorted = edge_list;
std::sort(edge_list_sorted.begin(), edge_list_sorted.end(),
[](const auto& a, const auto& b) { return std::get<0>(a) < std::get<0>(b); });
// Инициализация массивов
std::vector<int> xadj(num_vertices + 1, 0);
std::vector<int> adjncy;
std::vector<float> eweights;
if (weighted) {
adjncy.reserve(2 * num_edges);
eweights.reserve(2 * num_edges);
}
else {
adjncy.reserve(2 * num_edges);
}
// Заполняем xadj и adjncy
int current_vertex = 0;
xadj[0] = 0;
for (const auto& edge : edge_list_sorted) {
int u = std::get<0>(edge);
int v = std::get<1>(edge);
// Добавляем прямое ребро
adjncy.push_back(v);
if (weighted) {
eweights.push_back(std::get<2>(edge));
}
// Добавляем обратное ребро
adjncy.push_back(u);
if (weighted) {
eweights.push_back(std::get<2>(edge));
}
// Обновляем xadj для пропущенных вершин
while (current_vertex < u) {
current_vertex++;
xadj[current_vertex] = adjncy.size() - 1;
}
}
// Заполняем xadj для оставшихся вершин
for (int v = current_vertex + 1; v <= num_vertices; ++v) {
xadj[v] = adjncy.size();
}
return CRSGraph(vertex_dist, adjncy, xadj, weighted ? eweights : std::vector<float>());
}
};
Пример использования
int main() {
// Пример графа с 4 вершинами и 3 ребрами
std::vector<int> vertex_dist = { 0, 2, 4 }; // 2 процесса: 0-1 на процессе 0, 2-3 на процессе 1
std::vector<std::tuple<int, int, float>> edge_list = {
{0, 1, 5.0f},
{1, 2, 3.0f},
{2, 3, 2.0f}
}; // (u, v, weight)
// Создаем граф
CRSGraph graph = CRSGraph::from_edge_list(vertex_dist, edge_list, true);
// Получаем смежные вершины для вершины 1
auto adjacent = graph.get_adjacent_vertices(1);
std::cout << "Смежные с вершиной 1: ";
for (int v : adjacent) {
std::cout << v << " ";
}
std::cout << std::endl;
auto weights = graph.get_edge_weights(1);
std::cout << "Веса ребер для вершины 1: ";
for (float w : weights) {
std::cout << w << " ";
}
std::cout << std::endl;
// Получаем вершины для процесса 0
auto local_vertices = graph.get_local_vertices(0);
std::cout << "Вершины процесса 0: ";
for (int v = local_vertices.first; v < local_vertices.second; ++v) {
std::cout << v << " ";
}
std::cout << std::endl;
// Использование памяти
std::cout << "Использование памяти (байт): " << graph.memory_usage() << std::endl;
return 0;
}
Параллельный поиск в ширину на графе#
В классическом алгоритме BFS вершины графа обрабатываются по уровням, где каждый уровень представляет собой набор вершин, находящихся на одинаковом расстоянии от начальной вершины.
- Начальный уровень: Начинаем с вершины, которая является начальной.
- Следующий уровень: После того как все вершины текущего уровня обработаны, переходим к следующему уровню, который состоит из всех соседей вершин текущего уровня, которые ещё не были посещены.
В синхронизированном по уровням подходе весь уровень вершин обрабатывается одновременно, и переход к следующему уровню возможен только после завершения обработки текущего. Важно отметить, что такая синхронизация обеспечивается, например, с использованием очереди, где каждый элемент хранит информацию о текущем уровне.
Предположим, у нас есть граф, и мы начинаем обход с вершины 0. Ожидаем следующий порядок обработки:
- Уровень 0: Обрабатываем начальную вершину 0.
- Уровень 1: После обработки уровня 0 переходим к соседям вершины 0 (вершины 1 и 2).
- Уровень 2: После завершения уровня 1, обрабатываем соседей вершин 1 и 2 (например, вершина 3).
Этот процесс продолжается до тех пор, пока не будут обработаны все вершины
Препятствия для эффективной параллельной реализации#
Графы, используемые в практических приложениях, часто обладают нерегулярным шаблоном доступа к памяти. Это затрудняет их эффективную параллельную обработку, особенно когда данные распределены по нескольким узлам. В графах с малым диаметром, где вершины и ребра сильно связаны, значительные накладные расходы связаны с передачей данныхмежду процессом и потоком.
Прямой и обратный обходы#
В параллельных реализациях BFS важное место занимает выбор подхода к обходу графа. Рассмотрим два подхода: прямой обход и обратный обход.
Прямой обход#
В прямом обходе алгоритм начинает с начальной вершины и обрабатывает её соседей, а затем переходит к их соседям, продолжая процесс до тех пор, пока все вершины не будут посещены. Такой подход схож с традиционным алгоритмом BFS.
- Начальный уровень: Начинаем с вершины 0.
- Обработка уровня: На каждом уровне все вершины обрабатываются одновременно, в случае параллельной реализации — каждый поток отвечает за обработку части уровня.
- Переход к следующему уровню: После завершения обработки уровня, переходим к соседям, помечая их и добавляя в очередь.
void direct_bfs(const Graph& graph, int s, std::vector<int>& dist, std::vector<int>& pred) {
int N = graph.num_vertices;
std::vector<int> bitmap_current(N, 0); // Битмап для текущего уровня
std::vector<int> bitmap_next(N, 0); // Битмап для следующего уровня
dist.assign(N, -1); // Инициализация расстояний
pred.assign(N, -1); // Инициализация предшественников
dist[s] = 0; // Начальная вершина
bitmap_current[s] = 1; // Начальная вершина активна
int level = 0; // Уровень BFS
while (!check_end(dist)) {
for (int vert = 0; vert < N; ++vert) {
if (dist[vert] == -1 && bitmap_current[vert] == 1) { // Если вершина не была посещена
for (int neighb : graph.neighbors[vert]) { // Для каждого соседа
if (bitmap_current[neighb] == 1) { // Если сосед активен
dist[vert] = level + 1; // Устанавливаем расстояние
pred[vert] = neighb; // Устанавливаем предшественника
bitmap_next[vert] = 1; // Отмечаем вершину как активную на следующем уровне
break; // Прерываем, чтобы не проверять других соседей
}
}
}
}
// Обновляем битмапы для следующего уровня
bitmap_current = bitmap_next;
bitmap_next.assign(N, 0); // Сбрасываем битмап для следующего уровня
level++;
}
}
Обратный обход#
В обратном обходе задача меняет направление: неактивные вершины пытаются найти активные вершины среди своих соседей. Этот подход позволяет инвертировать традиционный процесс и, возможно, улучшить производительность на определённых типах графов.
- Активизация вершин: На каждом шаге неактивные вершины пытаются найти среди своих соседей активные вершины.
- Синхронизация: Как и в прямом обходе, переход к следующему уровню возможен только после того, как все вершины текущего уровня найдены.
Ресурс парраллелизации#
В приведенном вами коде потенциально можно параллелизовать несколько участков. Наиболее очевидная возможность для параллелизации — это обход вершин и обработка их соседей, так как эти операции можно выполнить независимо для каждой вершины. Рассмотрим подробнее, как это можно сделать.
Цикл по вершинам на текущем уровне: Внутри этого цикла для каждой вершины проверяется, если она активна и если её соседи активны. Поскольку для каждой вершины выполняется независимая операция, эту часть можно параллелизовать.
for (int vert = 0; vert < N; ++vert) {
if (dist[vert] == -1 && bitmap_current[vert] == 1) { // Если вершина не была посещена
for (int neighb : graph.neighbors[vert]) { // Для каждого соседа
if (bitmap_current[neighb] == 1) { // Если сосед активен
dist[vert] = level + 1; // Устанавливаем расстояние
pred[vert] = neighb; // Устанавливаем предшественника
bitmap_next[vert] = 1; // Отмечаем вершину как активную на следующем уровне
break; // Прерываем, чтобы не проверять других соседей
}
}
}
}
Этот цикл можно распараллелить, потому что операции для каждой вершины не зависят от других вершин. Например, можно использовать параллельный цикл с помощью OpenMP:
void direct_bfs(const Graph& graph, int s, std::vector<int>& dist, std::vector<int>& pred) {
int N = graph.num_vertices;
std::vector<int> bitmap_current(N, 0); // Битмап для текущего уровня
std::vector<int> bitmap_next(N, 0); // Битмап для следующего уровня
dist.assign(N, -1); // Инициализация расстояний
pred.assign(N, -1); // Инициализация предшественников
dist[s] = 0; // Начальная вершина
bitmap_current[s] = 1; // Начальная вершина активна
int level = 0; // Уровень BFS
while (!check_end(dist)) {
#pragma omp parallel for
for (int vert = 0; vert < N; ++vert) {
if (dist[vert] == -1 && bitmap_current[vert] == 1) { // Если вершина не была посещена
for (int neighb : graph.neighbors[vert]) { // Для каждого соседа
if (bitmap_current[neighb] == 1) { // Если сосед активен
dist[vert] = level + 1; // Устанавливаем расстояние
pred[vert] = neighb; // Устанавливаем предшественника
bitmap_next[vert] = 1; // Отмечаем вершину как активную на следующем уровне
break; // Прерываем, чтобы не проверять других соседей
}
}
}
}
// Обновляем битмапы для следующего уровня
bitmap_current = bitmap_next;
bitmap_next.assign(N, 0); // Сбрасываем битмап для следующего уровня
level++;
}
}
Гибридизация обхода [1]#
Для решения проблемы передачи данных можно использовать подоход, который чередует [1] прямой и обратный обход графа.
- Первые две итерации – “top-down”
- Следующие три итерации – “bottom-up”
- Остальные итерации – “top-down”
Код для тестирования приведен ниже
#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
#include <chrono>
#include <omp.h>
#include <cmath>
#include <iomanip>
enum State { TOP_DOWN, BOTTOM_UP };
struct CSRGraph {
std::vector<int> x; // offsets
std::vector<int> a; // adjacency list
int N; // number of vertices
int M; // number of edges (undirected)
CSRGraph(int n, int m) : N(n), M(m) {
x.resize(N + 1);
a.resize(2 * M);
}
};
// Generate RMAT graph (simplified)
CSRGraph generateRMATGraph(int scale, int edgeFactor) {
int N = 1 << scale;
int M = N * edgeFactor;
CSRGraph graph(N, M);
// Simplified RMAT generation (in practice use Graph500 generator)
#pragma omp parallel for
for (int i = 0; i < N; i++) {
graph.x[i] = i * edgeFactor;
for (int j = 0; j < edgeFactor; j++) {
graph.a[i * edgeFactor + j] = rand() % N;
}
}
graph.x[N] = 2 * M;
return graph;
}
void sequentialBFS(const CSRGraph& graph, int start, std::vector<int>& levels, std::vector<int>& parents) {
std::fill(levels.begin(), levels.end(), -1);
std::fill(parents.begin(), parents.end(), -1);
std::queue<int> q;
q.push(start);
levels[start] = 0;
while (!q.empty()) {
int current = q.front();
q.pop();
for (int i = graph.x[current]; i < graph.x[current + 1]; i++) {
int neighbor = graph.a[i];
if (levels[neighbor] == -1) {
levels[neighbor] = levels[current] + 1;
parents[neighbor] = current;
q.push(neighbor);
}
}
}
}
void parallelHybridBFS(const CSRGraph& graph, int start, std::vector<int>& levels,
std::vector<int>& parents, int num_threads) {
omp_set_num_threads(num_threads);
std::fill(levels.begin(), levels.end(), -1);
std::fill(parents.begin(), parents.end(), -1);
std::vector<int> q_curr, q_next;
q_curr.push_back(start);
levels[start] = 0;
State state = TOP_DOWN;
int level = 1;
const double alpha = 0.2, beta = 0.5;
const int factor = graph.M / graph.N / 2;
while (!q_curr.empty()) {
int visited = 0, in_level = 0;
q_next.clear();
if (state == TOP_DOWN) {
#pragma omp parallel for reduction(+:visited, in_level)
for (size_t i = 0; i < q_curr.size(); i++) {
int current = q_curr[i];
for (int j = graph.x[current]; j < graph.x[current + 1]; j++) {
int neighbor = graph.a[j];
in_level++;
#pragma omp critical
{
if (levels[neighbor] == -1) {
levels[neighbor] = level;
parents[neighbor] = current;
q_next.push_back(neighbor);
visited++;
}
}
}
}
}
else { // BOTTOM_UP
#pragma omp parallel for reduction(+:visited, in_level)
for (int current = 0; current < graph.N; current++) {
if (levels[current] == -1) {
for (int j = graph.x[current]; j < graph.x[current + 1]; j++) {
int neighbor = graph.a[j];
in_level++;
if (levels[neighbor] == level - 1) {
#pragma omp critical
{
levels[current] = level;
parents[current] = neighbor;
q_next.push_back(current);
visited++;
}
break;
}
}
}
}
}
// State transition logic
if (q_curr.size() < q_next.size()) { // Growing phase
if (state == TOP_DOWN && in_level < ((graph.N - visited) * factor + graph.N) / alpha) {
state = TOP_DOWN;
}
else {
state = BOTTOM_UP;
}
}
else { // Shrinking phase
if (q_next.size() < ((graph.N - visited) * factor + graph.N) / (factor * beta)) {
state = TOP_DOWN;
}
else {
state = BOTTOM_UP;
}
}
q_curr = q_next;
level++;
}
}
void testPerformance(int scale, int edgeFactor, int max_threads) {
CSRGraph graph = generateRMATGraph(scale, edgeFactor);
int N = graph.N;
std::cout << "\nScale: " << scale << " (N=" << N << ", M=" << graph.M << ")\n";
std::cout << "========================================\n";
std::vector<int> levels_seq(N, -1), parents_seq(N, -1);
auto start_seq = std::chrono::high_resolution_clock::now();
sequentialBFS(graph, 0, levels_seq, parents_seq);
auto end_seq = std::chrono::high_resolution_clock::now();
std::chrono::duration<double> seq_time = end_seq - start_seq;
std::cout << std::fixed << std::setprecision(4);
std::cout << "Sequential BFS time: " << seq_time.count() << " sec\n";
for (int threads = 1; threads <= max_threads; threads++) {
std::vector<int> levels_par(N, -1), parents_par(N, -1);
auto start_par = std::chrono::high_resolution_clock::now();
parallelHybridBFS(graph, 0, levels_par, parents_par, threads);
auto end_par = std::chrono::high_resolution_clock::now();
std::chrono::duration<double> par_time = end_par - start_par;
// Verify results
bool correct = (levels_seq == levels_par);
std::cout << "Parallel BFS (" << std::setw(2) << threads << " threads): "
<< par_time.count() << " sec, Speedup: "
<< seq_time.count() / par_time.count()
<< (correct ? "" : " [INCORRECT]") << "\n";
}
}
int main() {
const int max_threads = omp_get_max_threads();
std::cout << "System supports up to " << max_threads << " threads\n";
for (int scale = 10; scale <= 20; scale += 2) {
testPerformance(scale, 70, max_threads);
}
return 0;
}
Таблица тестирования
| Threads | Time (sec) | Speedup |
|---|---|---|
| Sequential | 0.0349 | - |
| 1 thread | 0.0242 | 1.4448 |
| 2 threads | 0.0247 | 1.4105 |
| 3 threads | 0.0248 | 1.4055 |
| 4 threads | 0.0241 | 1.4503 |
| 5 threads | 0.0248 | 1.4080 |
| 6 threads | 0.0246 | 1.4192 |
| 7 threads | 0.0244 | 1.4278 |
| 8 threads | 0.0238 | 1.4690 |
| 9 threads | 0.0245 | 1.4227 |
| 10 threads | 0.0241 | 1.4469 |
| 11 threads | 0.0233 | 1.4976 |
| 12 threads | 0.0237 | 1.4715 |
| 13 threads | 0.0243 | 1.4377 |
| 14 threads | 0.0244 | 1.4318 |
| 15 threads | 0.0251 | 1.3901 |
| 16 threads | 0.0236 | 1.4801 |
| 17 threads | 0.0243 | 1.4345 |
| 18 threads | 0.0246 | 1.4185 |
| 19 threads | 0.0246 | 1.4196 |
| 20 threads | 0.0239 | 1.4586 |
| 21 threads | 0.0248 | 1.4065 |
| 22 threads | 0.0245 | 1.4272 |
| 23 threads | 0.0238 | 1.4691 |
| 24 threads | 0.0242 | 1.4427 |
Поиск кратчайшего пути в графе#
Алгоритмы поиска кратчайшего пути в графе#
Алгоритм Дейкстры (Dijkstra)#
Теорема о высоте бинарного ориентированного дерева#
Бинарное ориентированное дерево с n листьями имеет высоту, не меньшую \log_{2}n.
Эта теорема имеет одно весьма интересное приложение. Предположим, что необходимо расположить строго по возрастанию элементы конечного линейно упорядоченного множества \{a_1,\ldots,a_n\}. Эту задачу называют задачей сортировки, а любой алгоритм, её решающий, — алгоритмом сортировки. С математической точки зрения алгоритм сортировки должен найти такую перестановку \{a_{i_1},\ldots,a_{i_n}\} элементов множества, которая была бы согласована с заданным на нём отношением \leqslant линейного порядка, т.е. для любых k,l из справедливости неравенства i_k < i_l должно следовать a_{i_k} \leqslant a_{i_l}.
Первоначально сортируемые элементы могут быть расположены в произвольном порядке, т.е. исходной может быть любая перестановка элементов сортируемого множества, и мы не имеем никакой априорной информации об этой перестановке. Единственный способ получить такую информацию — проводить попарные сравнения элементов a_i (относительно рассматриваемого линейного порядка) в какой-либо последовательности. Заметим, что при этом совершенно не обязательно проводить все возможные сравнения, т.е. сравнивать a_i с a_j для всех i \ne j. Например, можно использовать транзитивность отношения порядка.
Все сравнения, которые в принципе могут быть проведены в процессе работы некоторого алгоритма, изображаются наглядно в виде ориентированного дерева, называемого деревом решений. На рис. 5.17 приведено дерево решений для трехэлементного множества \{a,b,c\}. Вершины ориентированного дерева, не являющиеся листьями, помечены проверяемыми неравенствами, а множество листьев находится во взаимно однозначном соответствии с множеством всех перестановок исходного множества.
Дерево решений для трехэлементного множества {a,b,c}
Поскольку в результате сортировки может получиться любая перестановка исходного множества и каждой такой перестановке соответствует лист дерева решений, в общем случае количество листьев будет равно n! — количеству перестановок n-элементного множества.
Следовательно, сортируя входную последовательность, алгоритм обязательно пройдет какой-то путь от корня дерева решений к одному из листьев, и, таким образом, число операций сравнения (число шагов алгоритма сортировки) будет величиной, пропорциональной высоте дерева решений, не меньшей чем \log_{2}n!, в силу теоремы 5.2.
Используя для оценки факториала при больших n формулу Стирлинга
получаем, что дерево решений имеет высоту порядка n\log_{2}n.
Таким образом, в общем случае задачу сортировки с помощью попарных сравнений нельзя решить быстрее, чем за указанное число шагов. Безусловно, конкретный путь в дереве решений из корня к одному из листов зависит от исходной перестановки. Например, в дереве решений, приведенном на рис. 5.17, есть два "коротких" пути длины 2, однако остальные пути имеют длину 3.
Заметим, что в общем случае ориентированное дерево — это не связный ориентированный граф. Компонентами ориентированного дерева являются его подграфы, порожденные множеством вершин, расположенных на некотором пути из корня в лист.
Список источников#
- Черноскутов, М. А. Параллельная высокопроизводительная обработка графов / М. А. Черноскутов // Параллельные вычислительные технологии (ПаВТ'2016) : труды международной научной конференции, Архангельск, 28 марта – 01 2016 года. – Архангельск: Издательский центр ЮУрГУ, 2016. – С. 736-742. – EDN VSRRSD.