Элементарные алгоритмы для работы с графами

Презентация Лекция 7

История возникновения теории графов

Теория графов — это область математики, которая использует абстракции для описания различных систем, состоящих из объектов, соединённых связями. Она оперирует такими понятиями, как вершины (или узлы) и рёбра (или линии), которые соединяют эти вершины. Графы стали важным инструментом для изучения взаимосвязей и структуры в самых разных областях науки и техники. Теория графов удобна для начинающих, потому что она:

• Геометрически наглядна: графы легко представлять в виде рисунков, что позволяет легко понять их структуру.
• Математически содержательна: несмотря на свою простоту, теория графов затрагивает множество фундаментальных математических идей и понятий.
• Не требует сложных математических инструментов: базовые принципы теории графов можно понять без углубленного изучения сложных математических теорий.

Как и теория чисел, теория графов концептуально проста, но порождает сложные и нерешённые проблемы. Эта область, как и геометрия, обладает визуальной привлекательностью и широким спектром приложений, что делает её идеальным предметом для включения в учебные программы по математике.

Возникновение теории графов связано с задачами, которые на первый взгляд могли показаться лишь математическими головоломками. Так же, как и теория вероятностей, она начинала своё развитие в контексте игр и развлечений, прежде чем стать серьёзной областью научных исследований. Эту параллель можно провести и с развитием других математических областей, которые также начинались с прикладных проблем, связанных с азартными играми.

Теперь давайте рассмотрим краткую хронологию ключевых событий, которые сыграли важную роль в становлении теории графов.

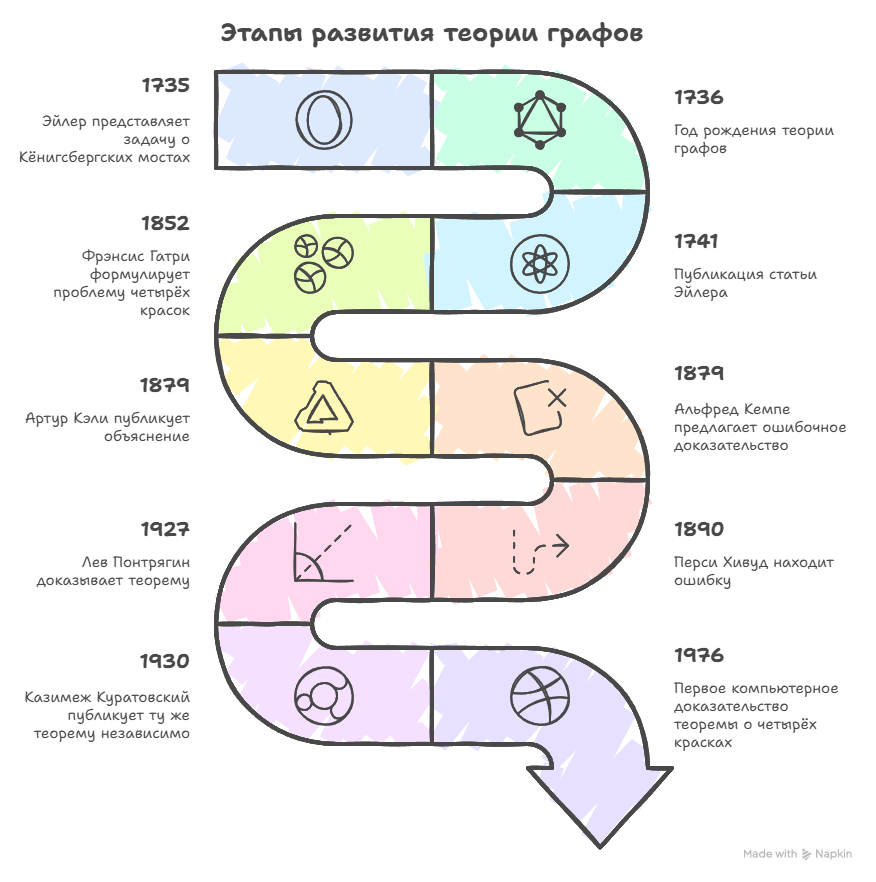
Для тех, кому удобнее читать таблицей:

Год	Событие
1735	Эйлер представляет статью по задаче Кёнигсбергских мостов в Петербургской академии наук. Эта задача считается первой задачей, решённой с использованием графов. Задача заключалась в том, чтобы пройти по всем мостам города, не переходя по одному из них дважды. Эйлер показал, что это невозможно, сформулировав основные принципы теории графов.
1736	Год рождения теории графов. Эйлер доказал, что задачу о Кёнигсбергских мостах невозможно решить, если использовать правила обхода графов, и заложил основы теории, определив графы как математическую структуру для решения подобных задач. Это событие считается началом развития теории графов.
1741	Публикация статьи Эйлера. В своей работе Эйлер подробно изложил результаты своих исследований и математические методы, которые позволяли решать задачи, подобные задаче о Кёнигсбергских мостах. Эта работа стала основой для дальнейшего развития теории графов и её применения в различных областях.
1852	Френсис Гатри формулирует проблему четырёх красок. Это стало важным моментом в теории графов, поскольку задача заключалась в доказательстве того, что любую карту можно раскрасить не более чем четырьмя цветами, так чтобы соседние области не имели одинакового цвета.
1879	Артур Кэли публикует объяснение задачи четырёх красок с использованием методов теории графов. Он предложил идею, что задачу о четырёх красках можно рассматривать через графы, где области карты — это вершины, а соседние области — рёбра.
1879	Альфред Кемпе предлагает ошибочное доказательство теоремы о четырёх красках, которое позже будет опровергнуто. Это доказательство было широко принято на протяжении нескольких десятилетий, пока не было найдено множество ошибок в его рассуждениях.
1890	Перси Хивуд находит ошибку в доказательстве Кемпе и публикует собственное объяснение задачи. Хивуд показал, что теорема о четырёх красках верна, если вместо четырёх использовать пять цветов, а также обобщил понятие карты с плоскости на другие поверхности.
1927	Лев Понтрягин доказывает теорему Понтрягина — Куратовского, связанную с планарностью графов, хотя работа не была опубликована сразу. Это доказательство имело важное значение для изучения структуры графов, которые можно разместить на плоскости без пересечений рёбер.
1930	Казимеж Куратовский публикует теорему Понтрягина — Куратовского независимо от Понтрягина. Теорема стала важной в исследовании планарности графов, предлагая критерии для определения, может ли граф быть нарисован на плоскости без пересечений рёбер.
1936	Первая книга по теории графов — Денеш Кёниг «Теория конечных и бесконечных графов». Эта работа стала основным трудом по теории графов на несколько десятилетий, в которой Кёниг систематизировал знания о графах и их свойствах.
1968	Группа математиков из разных стран доказала гипотезу Хивуда, связанную с четырёхцветной задачей. Это доказательство стало важным шагом в теории графов, решив одну из самых известных проблем в этой области.
1976	Первое компьютерное доказательство теоремы о четырёх красках. Используя компьютерные технологии, группа математиков доказала, что четыре цвета достаточно для раскраски любой карты. Это было первым случаем использования вычислительных методов для доказательства математической теоремы.
1977	Фрэнк Харари основал журнал «Теория графов», который стал важным источником для публикации новых исследований в области графов. Журнал активно развивал научные работы и публиковал инновационные подходы в решении задач с графами.

Древние прообразы графов

Считается, что графоподобные структуры использовались человечеством ещё в глубокой древности, хотя сами графы как математическая концепция ещё не существовали. Одним из самых ранних примеров графов является генеалогическое древо. Оно использовалось для наглядного отображения родственных связей и передачи знаний о происхождении и принадлежности к определённым родам или семьям. В генеалогических деревьях элементы, такие как родственные связи или поколения, изображаются в виде вершин, а линии, соединяющие эти вершины, представляют рёбра, символизирующие связи между поколениями. Эта структура схожа с современными графами, где вершины — это объекты, а рёбра — их отношения или взаимодействия.

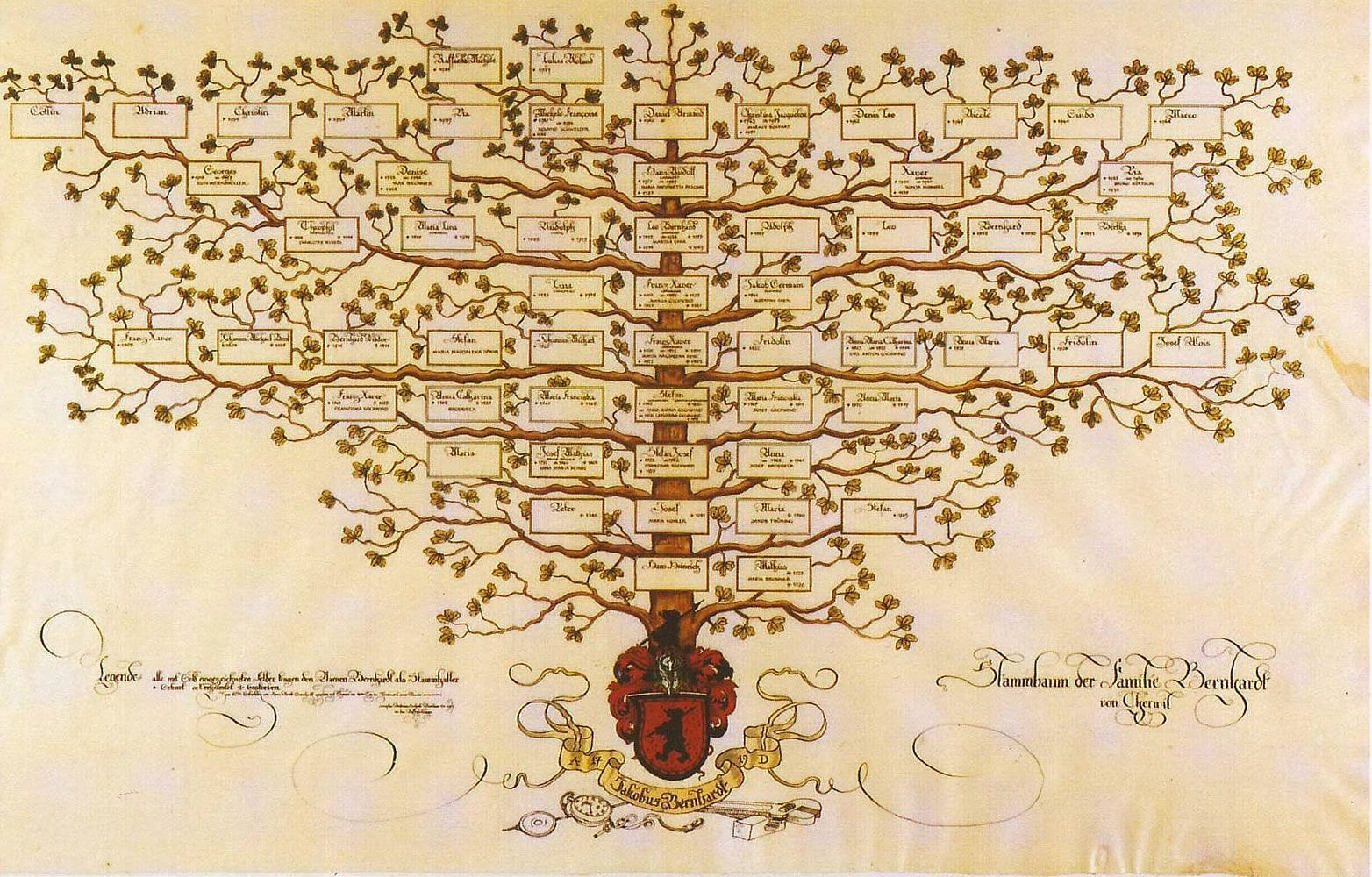
Генеалогическое древо помогало людям не только отслеживать родственные отношения, но и обозначать социальные, политические или даже религиозные связи, которые, по сути, можно рассматривать как графовые связи между различными элементами. Это наглядное представление позволило удобнее и быстрее ориентироваться в семейных отношениях, что было крайне важно для древних обществ.

Другим примером применения графоподобных структур в древности являются созвездия. Небо, усеянное звёздами, часто изображалось в виде связных объектов, которые соединялись воображаемыми линиями. Эти линии образовывали созвездия, которые, несмотря на отсутствие строгой математической формализации, являются графами, где звёзды — вершины, а соединяющие их линии — рёбра. Такие структуры использовались в астрономии для навигации, а также в мифологии, где каждое созвездие рассказывало свою историю.

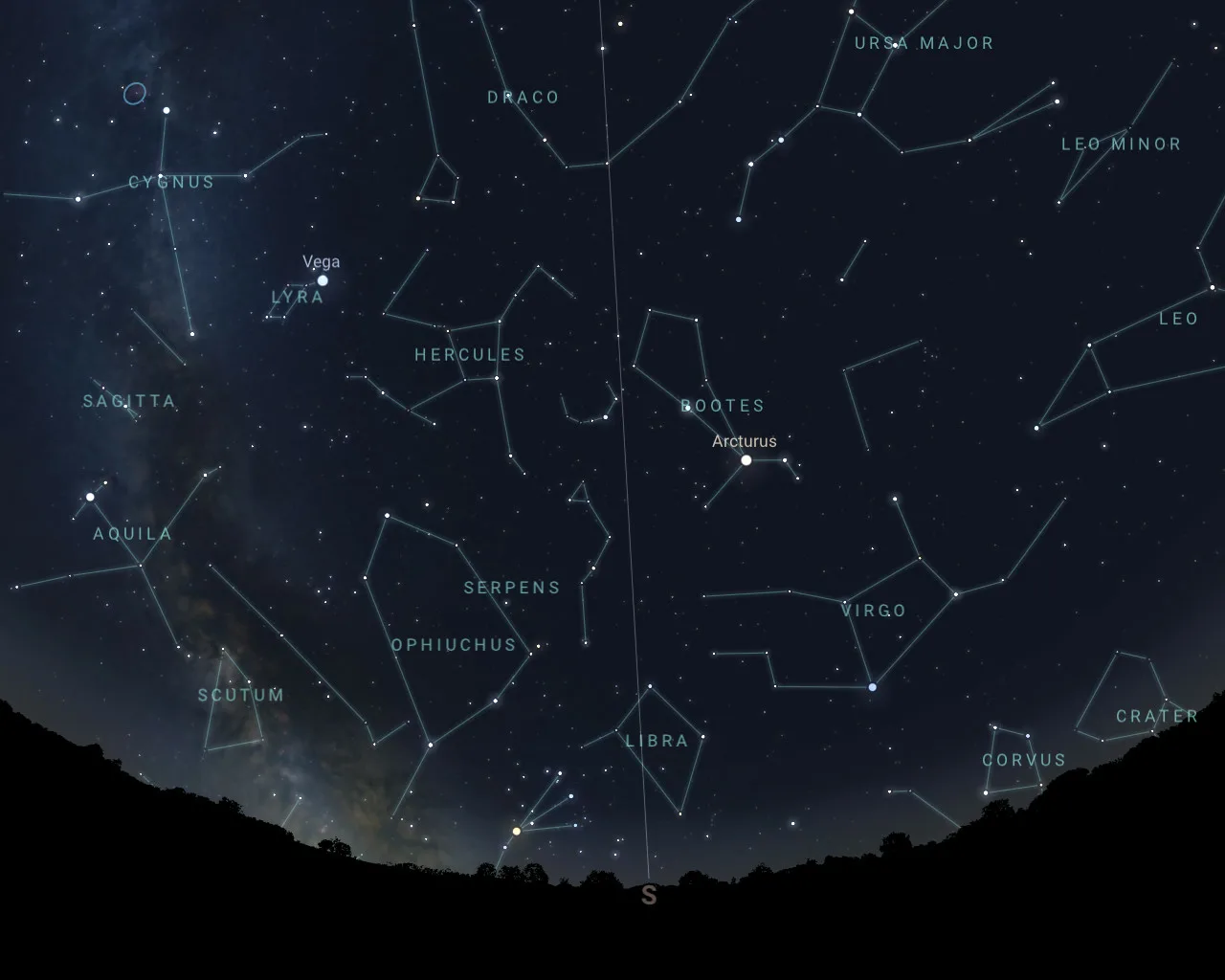
Созвездия представляли собой особую форму графа, которая была не только геометрически привлекательной, но и содержала культурные, мифологические и навигационные значения. Как и в случае с генеалогическими деревьями, созвездия иллюстрируют использование графов для организации и упорядочивания информации, несмотря на отсутствие математических понятий графов в те времена. Эти прообразы графов оказали большое влияние на развитие научных концепций и нашли своё место в дальнейшем становлении теории графов.

Первое использование и «открытие» теории графов

Задача о Кёнигсбергских мостах, предложенная в XVIII веке, стала отправной точкой для появления теории графов. Этот интересный и на первый взгляд простейший вопрос о том, можно ли пройти по всем мостам города Кёнигсберга, не переходя по одному из них дважды, привёл к значительному открытию в математике. Вопрос возник из-за того, что Кёнигсберг был разделён на несколько островов, которые соединялись семью мостами, и жители города задавались вопросом, возможно ли пройти по всем этим мостам, не повторяя путь по ним.

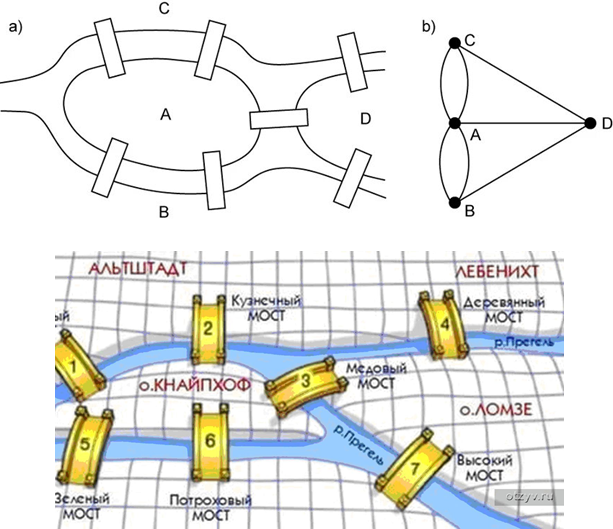
Для решения задачи требовался новый подход, который выходил за рамки традиционных геометрических методов того времени. Проблема, на первый взгляд, была исключительно практической, но на самом деле она скрывала в себе более глубокие математические принципы. Вопрос, поставленный перед горожанами, не был разрешим с помощью традиционных методов. Однако оно стало ключом к созданию новой области математики, которая будет изучать структуры, подобные сети мостов в Кёнигсберге.

В 1735 году этот вопрос привлек внимание одного из величайших математиков того времени — Леонарда Эйлера. Эйлер, работавший в Петербургской академии наук, предложил новый способ рассмотрения задачи. Он сформулировал её с помощью математической модели, которая теперь известна как граф. Эйлер предложил представить острова как вершины графа, а мосты между ними — как рёбра, соединяющие эти вершины. Задача сводилась к нахождению пути, который проходил бы по каждому ребру графа ровно один раз, что в математике называется Эйлеровым путём.

Чтобы понять, может ли такой путь существовать в данном графе, Эйлер ввёл понятие степени вершины — количества рёбер, ведущих в эту вершину. Эйлер доказал, что в графе может быть только две вершины с нечётной степенью, если по нему существует такой путь. Однако в случае с Кёнигсбергом было четыре вершины с нечётной степенью, что означало, что решить задачу невозможно.

Это решение стало важным этапом в развитии математического анализа, потому что Эйлер показал, что задачи, которые раньше решались с помощью геометрических методов, могут быть также решены с помощью абстракции, введя концепцию графов. Эйлер не только доказал невозможность решения задачи, но и сформулировал важное математическое общее правило, которое теперь является основой теории графов.

Важным событием стало представление Эйлером своей работы на конференции Петербургской академии наук 26 августа (6 сентября) 1735 года. В этот день Эйлер представил фрагмент своей статьи под названием “Solutio problematis ad geometriam situs pertinentis” («Решение одной задачи, связанной с геометрией положения»). Статья была посвящена решению задачи о Кёнигсбергских мостах, и её доклад стал первым официальным сообщением по теории графов. В конференции участвовали ведущие учёные того времени, среди которых были Христиан Гольдбах, Жозеф Никола Делиль, Георг Вольфганг Крафт, а также сам Эйлер.

Протокол заседания конференции, сохранившийся до наших дней, свидетельствует о том, как прошло это важное событие. По сообщениям протокола, перед докладом Эйлера библиотекарь Шумахер объявил присутствующим, что профессор Эйлер будет читать свою статью. После доклада, как указано в протоколе, конференц-секретарь Гольдбах оттискнул на копии статьи отметку «представлено», что означало официальное принятие работы.

Этот доклад Эйлера стал важным моментом в истории математики, так как благодаря ему была заложена основа для всей теории графов. Решение задачи о Кёнигсбергских мостах открыло новые возможности для исследования структур, которые связаны с сетями, и заложило основы для дальнейших математических и практических исследований в самых разных областях науки и техники.

Второе и третье «открытие» графов

После открытия Эйлера, теория графов продолжала развиваться, и в XIX веке произошло два важнейших шага в её становлении, которые стали значимыми для разных областей науки.

В 1847 году немецкий физик Густав Кирхгоф, исследуя проблемы электрических цепей, фактически разработал теорию деревьев. Он занимался нахождением силы тока в каждом контуре электрической цепи с помощью системы уравнений. При этом Кирхгоф не рассматривал электрическую цепь как сложную систему с множеством взаимодействующих элементов, а вместо этого использовал граф. Это позволило ему упростить задачу, так как для решения системы уравнений не было необходимости анализировать каждый цикл графа. Вместо этого Кирхгоф показал, что достаточно рассматривать независимые циклы, которые могут быть определены через любой остовное дерево графа. Этот подход стал важным шагом в развитии теории графов, так как связал её с практическими задачами в физике.

Через десять лет, в 1857 году, английский математик Артур Кэли открыл важный класс графов, а именно деревья, в контексте органической химии. Кэли занимался перечислением химических изомеров, то есть углеводородов с фиксированным числом атомов углерода, которые принадлежат к классу насыщенных углеводородов (алканов). Задача Кэли заключалась в поиске всех возможных структур этих молекул, что требовало учёта их возможных структурных изомеров. В результате своей работы он установил, что каждая молекула может быть представлена как дерево, то есть как граф, в котором отсутствуют циклы, а все вершины соединены в единую структуру. Это открытие имело важное значение не только для химии, но и для дальнейшего развития теории графов.

Таким образом, работы Кирхгофа и Кэли стали ключевыми моментами в развитии теории графов, применяя её для решения проблем в физике и химии, и значительно расширили область применения графов в различных науках.

Четвёртое «открытие» графов

В 1859 году ирландский математик сэр Уильям Гамильтон придумал игру под названием «Вокруг света», которая использовала додекаэдр — многогранник с 20 вершинами, каждая из которых соответствовала известному городу. Задача игрока заключалась в том, чтобы пройти по рёбрам додекаэдра, посетив каждую вершину ровно один раз, не повторяя пути.

Эта игра, на первый взгляд, казалась простой развлекательной задачей, однако её решение было связано с глубокими математическими принципами. Задача Гамильтона фактически сводилась к нахождению Гамильтонова пути в графе. В теории графов Гамильтонов путь — это такой путь, который проходит через все вершины графа, не посещая ни одну вершину более одного раза.

Идея Гамильтона о нахождении пути, проходящего через все вершины графа, была не только математически интересной, но и стала основой для дальнейших исследований в теории графов. Задача, предложенная Гамильтоном, привела к разработке важного понятия — Гамильтонова пути и Гамильтонова цикла (когда путь замкнут и возвращается в исходную вершину). Эти понятия стали центральными в теории графов и нашли широкое применение в различных областях, например, в задачах логистики, планирования маршрутов и даже в поисковых алгоритмах.

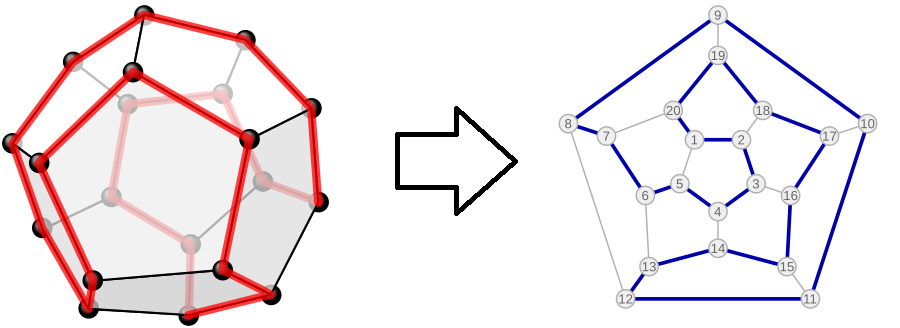
Гамильтонов подход был полезен не только в теории графов, но и в реальных задачах. Например, при планировании оптимальных маршрутов для доставки товаров или в задачах, связанных с оптимизацией транспортных сетей.

Таким образом, игра «Вокруг света» Гамильтона не только занимала воображение людей того времени, но и сыграла важную роль в развитии теории графов. Её математическая суть стала основой для изучения сложных маршрутов в графах и расширила горизонты применения теории графов в самых разных областях науки и практики.

Начало систематического использования слова «граф» и диаграмм графов

Начало систематического использования слова «граф» и диаграмм графов связано с работой венгерского математика Денеша Кёнига, который в начале XX века предложил называть различные схемы «графами» и изучать их общие свойства. Это стало важным шагом в формализации и систематизации теории графов, которая ранее использовалась в различных областях, но ещё не имела единого термина и четкой концептуальной структуры.

В 1936 году вышла первая в мире книга по теории графов на немецком языке под авторством Кёнига — «Теория конечных и бесконечных графов». Эта работа стала основополагающей для дальнейшего развития теории графов как самостоятельной области математики. Книга Кёнига описала не только основные понятия графов, такие как вершины и рёбра, но и принципы их анализа, а также важные теоремы, которые позже стали краеугольными камнями теории графов.

Кёниг ввёл систематическое использование термина «граф» для обозначения любых абстрактных структур, состоящих из множества объектов (вершин) и связей между ними (рёбер), и предложил методы их исследования. Это дало начало развитию целой области математики, в которой графы стали не просто абстракциями, а объектами, требующими глубокого математического анализа.

Работа Кёнига оказала огромное влияние на дальнейшее развитие теории графов и привела к широкому применению графов в различных научных и практических областях, таких как теория сетей, информатика, биология и многие другие.

Графовая теория в современности

В современном мире мы всё чаще сталкиваемся с необходимостью описания сложных взаимосвязей между объектами. Это касается не только IT или социальных сетей — даже привычная дорожная сеть представляет собой систему с множеством узлов и связей между ними. Как формализовать такую структуру? Как анализировать, строить маршруты, находить оптимальные пути? Ответ даёт графовая теория

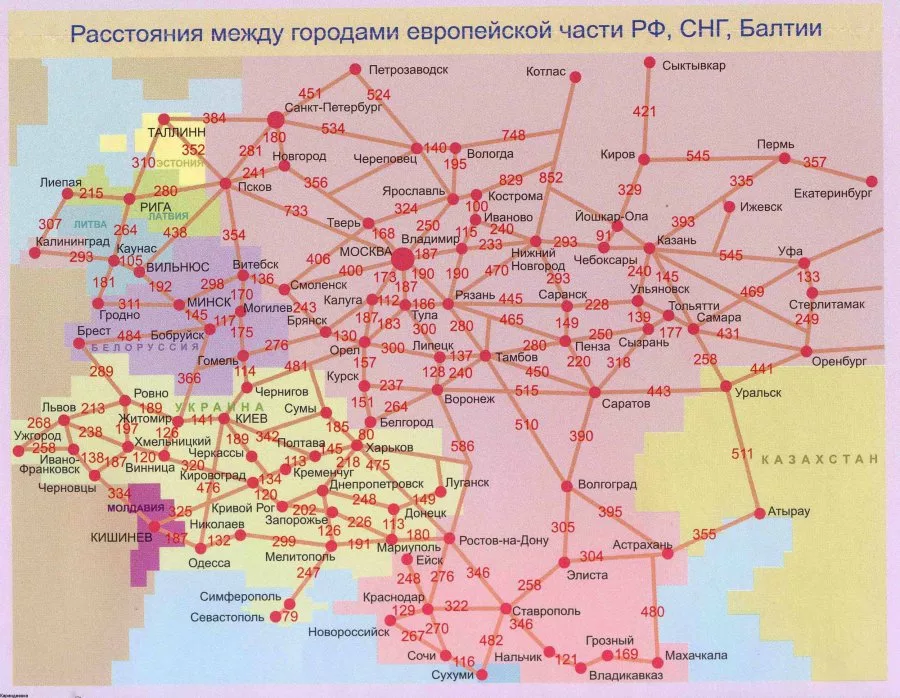
Моделирование дорожно-транспортной инфраструктуры

Один из ярких примеров её применения — моделирование дорожно-транспортной инфраструктуры. При этом транспортная система представляется в виде графа:

• Вершины графа соответствуют городам, транспортным узлам, перекрёсткам.
• Рёбра — это дороги, маршруты или другие соединения между узлами.
• Веса рёбер могут отражать расстояние, стоимость проезда, время в пути и другие параметры.

Таким образом, граф становится абстрактной, но удобной моделью, позволяющей проводить анализ транспортной сети, оценивать её эффективность, выявлять узкие места и оптимизировать маршруты.

На приведённой ниже схеме каждая вершина — это город, а ребро между ними содержит информацию о расстоянии. Такая модель может служить основой для алгоритмов поиска кратчайшего пути, анализа связности и других задач.

Социальный граф: распространение информации в сетях

Графовая теория также активно применяется в анализе социальных сетей. Пользователи платформ вроде VK, Telegram формируют сложную структуру связей: они подписываются друг на друга, обмениваются сообщениями, делятся контентом. Всё это можно представить в виде социального графа.

В социальной сети:

• Вершины — это пользователи.
• Рёбра — связи между ними (например, подписки или дружба).
• Дополнительно можно учитывать направление связи (кто на кого подписан), вес связи (частота взаимодействия, степень влияния и т. п.).

На следующей схеме изображён фрагмент социального графа. Он помогает понять, как распространяется информация — по каким путям она передаётся от одного пользователя к другому.

Особый интерес представляет механизм вирусного распространения информации — когда один пользователь публикует пост, и он начинает быстро расходиться по сети. Такой процесс можно смоделировать с помощью каскадов — цепочек репостов и пересылок.

На следующей визуализации показано, как от одного источника контент распространился по сети: пользователи пересылали его друг другу, формируя разветвлённую структуру.

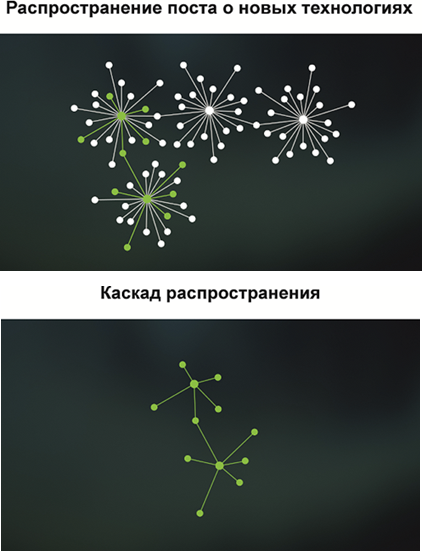
Анализ каскадов помогает понять, какие узлы графа играют ключевую роль в распространении информации, как влияют структуральные особенности графа на скорость и охват, и как можно управлять информационными потоками в сети.

Граф как инструмент научного анализа

Графовая модель — это не только способ описания физической или социальной структуры, но и мощный инструмент для анализа сложных систем и больших объёмов данных. Многие исследовательские задачи сводятся к построению графа и последующему анализу его свойств.

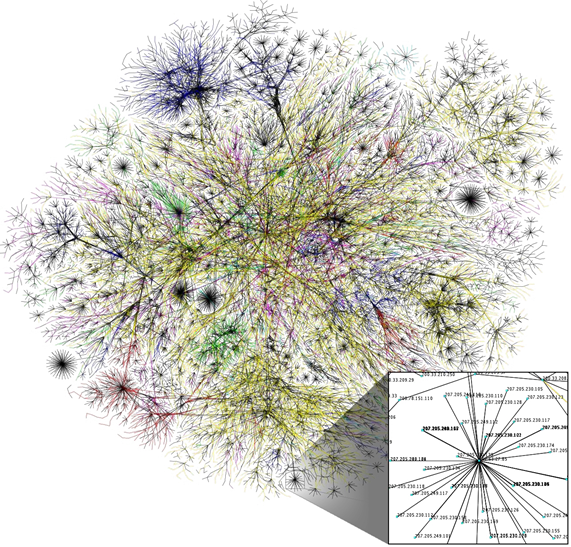
Пример 1: Граф интернета

На изображении ниже — частичная карта интернета, основанная на данных от 15 января 2005 г. (источник: opte.org).
Здесь:

• Вершины графа — IP-адреса узлов в интернете.
• Рёбра — маршруты между узлами.
• Длина рёбер — отражает временную задержку (ping) между узлами.

Такая визуализация позволяет изучать структуру интернета как распределённой сети, выявлять кластеры, узлы с высокой степенью связанности, потенциальные точки отказа.

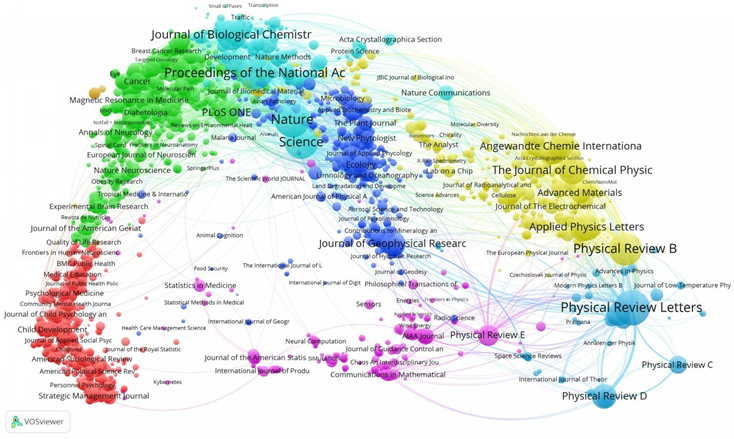
Пример 2: Граф цитирования научных публикаций

Другой пример — граф цитат между научными журналами. На визуализации (построенной с помощью VOSviewer) представлены:

• Вершины — научные журналы.
• Рёбра — факт цитирования публикаций между ними.

На изображении показано 5000 наиболее цитируемых журналов за период с 1980 по 2016 годы. Такая карта позволяет исследовать структуру научных дисциплин, выявлять влиятельные издания, отслеживать междисциплинарные связи.

Источник:
Van Eck N. J., Waltman L. Visualizing freely available citation data using VOSviewer // CWTS Blog, 2017. https://www.cwts.nl/blog?article=n-r2r294

Онтологические графы

Графы применяются не только для описания физических или социальных структур, но и для представления знаний. В таких случаях речь идёт об онтологиях — формализованных структурах, описывающих понятия и отношения между ними.

Онтология — это структура, в которой фиксируются понятия некоторой предметной области и связи между ними. Граф здесь служит средством для логической организации знаний.

В онтологическом графе:

• Вершины — это понятия (классы, термины, сущности).
• Рёбра — отношения между понятиями (например, "является", "состоит из", "входит в", "взаимодействует с").
• Такой граф, как правило, ориентированный и может содержать иерархию.

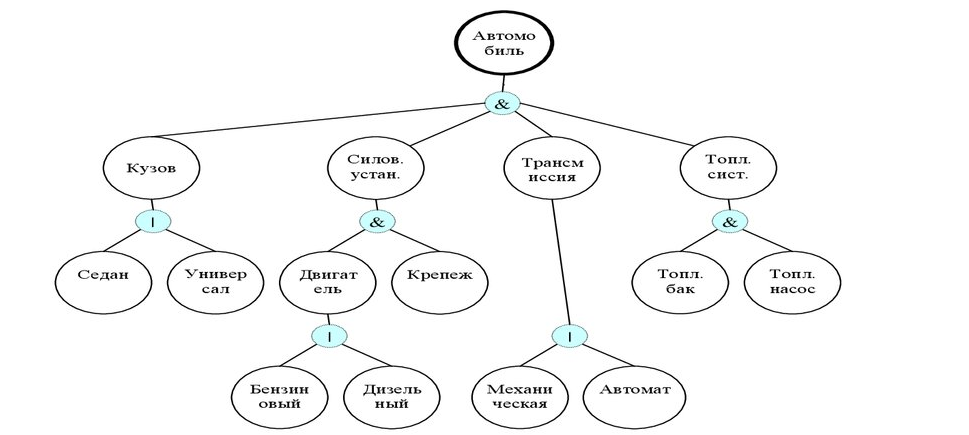
Пример: онтология автомобиля

На схеме ниже показано, как можно представить знания о транспортном средстве в виде онтологического графа. Видны ключевые компоненты (двигатель, кузов и т. п.) и связи между ними. Это позволяет систематизировать информацию и использовать её, например, в экспертных системах или системах поиска.

Пример: онтология компьютерных вирусов

Подобные графы применяются и в области информационной безопасности. Онтология компьютерных вирусов отражает классификацию типов угроз, способы распространения, механизмы заражения и защиты.

Онтологические графы применяются в семантическом вебе, системах искусственного интеллекта, классификаторах, а также при построении справочных и обучающих систем.

Графовая теория - вечно живая область математики (или почему Почему графами занимается Nvidia?)

В 2017 году компания Nvidia опубликовала технический отчёт под названием «Parallel Depth-First Search for Directed Acyclic Graphs» (NVR-2017-001).
Это может вызвать вопрос: зачем производителю видеокарт изучать алгоритмы на графах?

Ответ в том, что современные графические процессоры (GPU) используются не только для рендеринга изображений, но и как универсальные ускорители для параллельных вычислений. А многие задачи на графах плохо распараллеливаются — например, обходы графа (DFS, BFS), построение топологической сортировки, поиск компонент.

В частности, ориентированные ациклические графы (DAG) встречаются в компиляторах, системах обработки данных, задачах планирования и машинного обучения.

Чтобы эффективно решать такие задачи на GPU, Nvidia и исследует специализированные алгоритмы — с учётом архитектуры видеокарт.

Таким образом, даже такая «академическая» задача, как обход графа в глубину, становится актуальной в контексте высокопроизводительных вычислений.
Это ещё раз подчёркивает: графовая теория — не только про математику, но и про будущее вычислений.

Основы графовой теории. Основные определения

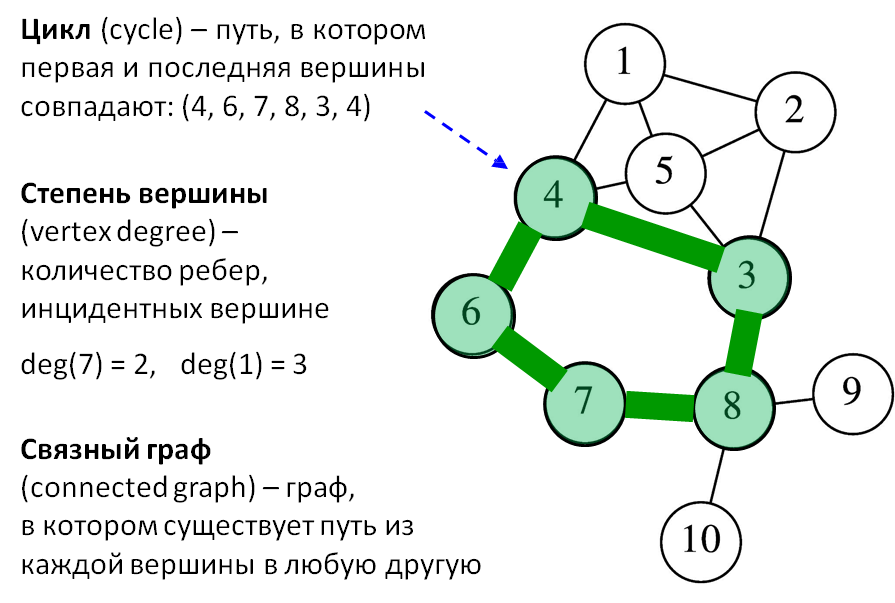
Одним из важнейших объектов в теории графов является вершина (vertex, node) — точка, обозначающая некий объект или элемент множества. Вершины соединяются между собой рёбрами (edge, link), которые показывают наличие связи между двумя объектами.

Если две вершины соединены ребром, они называются смежными (adjacent vertices). Например, если в графе есть ребро (4, 6), то оно инцидентно (incident) вершинам 4 и 6. Это означает, что вершины 4 и 6 связаны напрямую.

Когда мы говорим о пути (path) в графе, мы имеем в виду последовательность вершин, в которой каждая следующая вершина соединена с предыдущей ребром. При этом все вершины и рёбра в таком пути различны. Путь играет ключевую роль при анализе структуры графа и при решении задач на перемещение или распространение информации.

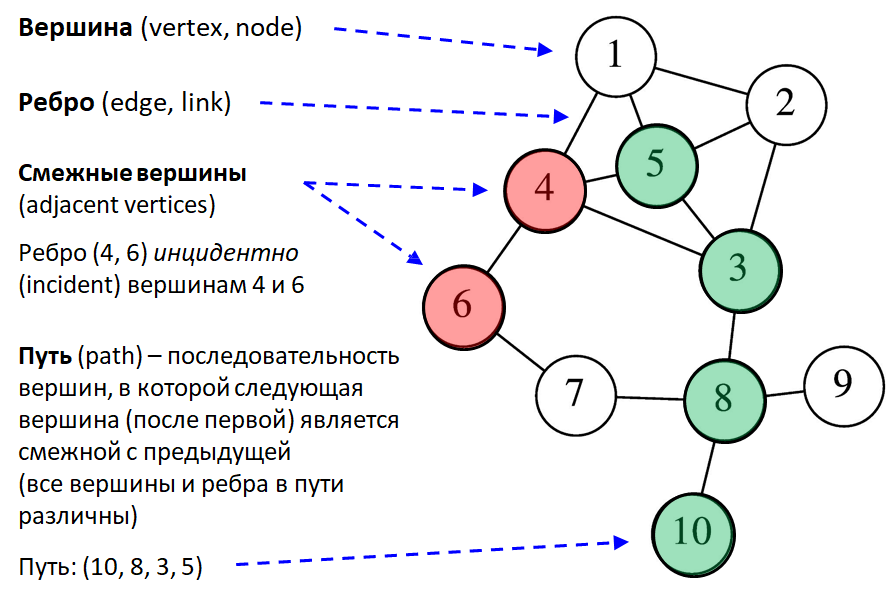
В отличие от пути, цикл (cycle) — это замкнутая последовательность вершин, в которой начальная и конечная вершины совпадают. Например, последовательность (4, 6, 7, 8, 3, 4) является циклом.

Ещё одно базовое понятие — степень вершины (vertex degree), которая показывает, сколько рёбер инцидентно данной вершине. Иными словами, это число прямых связей, идущих из вершины. Например:
- deg(7) = 2
- deg(1) = 3

Особое внимание уделяется тому, является ли граф связным (connected graph). Граф считается связным, если из любой вершины можно добраться до любой другой, то есть между каждой парой вершин существует путь.

Виды графов

Существует несколько ключевых разновидностей графов, каждая из которых используется для моделирования различных задач.

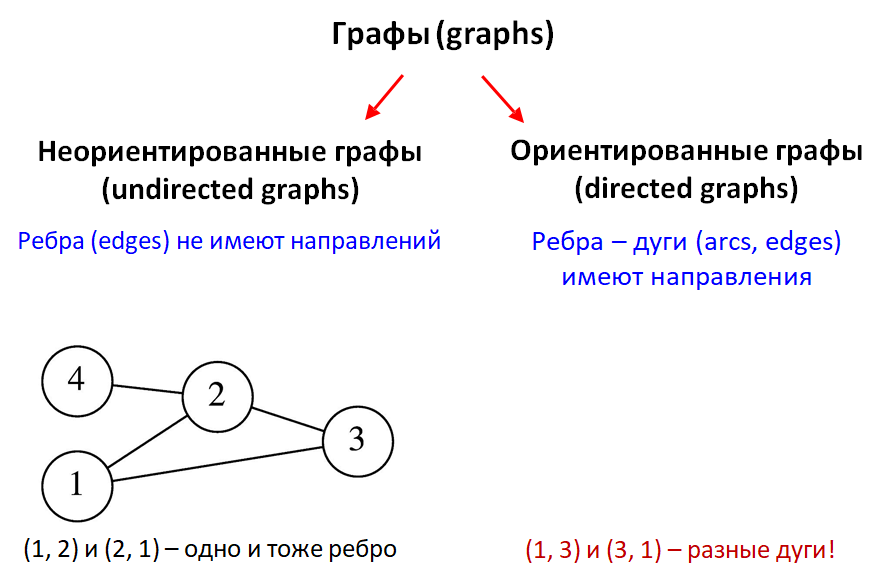
Первое различие — направленность.
Если рёбра имеют направление (указано стрелками), такой граф называется направленным графом (directed graph или орграф).
Если же направление отсутствует, и рёбра изображаются в виде обычных линий, то такой граф называется ненаправленным (undirected graph).

Следующее важное понятие — взвешенный граф (weighted graph).
В таком графе каждому ребру (или дуге) присваивается числовое значение — вес.
Вес ребра между вершинами i и j обозначается как wᵢⱼ. Вес может отражать расстояние, стоимость, время или иную величину.

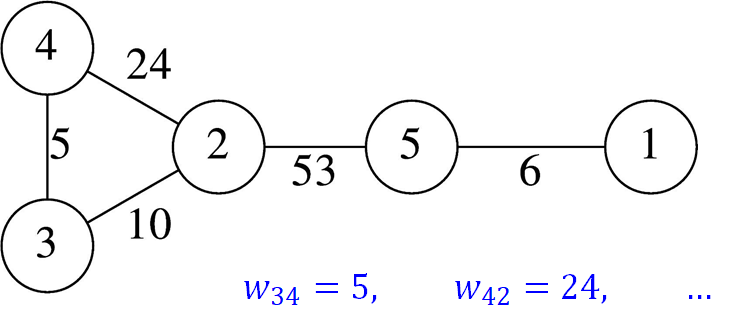
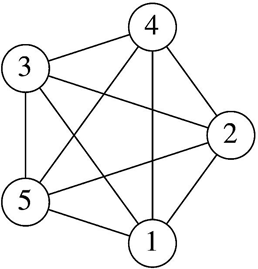
Также выделяют полный граф — граф, в котором каждая вершина соединена с каждой другой.

При изучении структуры графа важным понятием является насыщенность графа D.
Насыщенность показывает, насколько «плотно» вершины соединены рёбрами. В зависимости от количества рёбер граф может быть:

• насыщенным, если количество рёбер близко к максимальному возможному,
• разреженным, если количество рёбер существенно меньше возможного максимума.

Представление графов в памяти

Способ хранения графа в памяти напрямую влияет на эффективность выполнения алгоритмов: от него зависят как вычислительная сложность операций, так и объём используемой памяти.
Существует два основных подхода к представлению графов:

• Матрица смежности (adjacency matrix) — подходит для насыщенных графов, в которых множество рёбер почти максимально.
• Списки смежных вершин (adjacency list) — эффективны для разреженных графов, в которых рёбер гораздо меньше, чем максимально возможное количество.

Матрица смежности

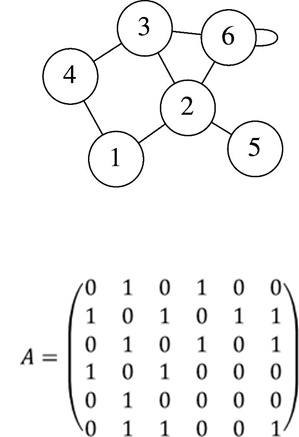
Матрица смежности представляет собой таблицу, в которой каждая строка и каждый столбец соответствуют вершинам графа. Если между двумя вершинами существует ребро, то в соответствующей ячейке матрицы стоит единица, в противном случае — ноль.
Такой способ представления позволяет моментально определить наличие или отсутствие ребра между двумя вершинами. Он особенно удобен при работе с насыщенными графами, в которых рёбер много — почти столько же, сколько могло бы быть теоретически (порядка квадрата числа вершин).

Матрица смежности требует O(V²) памяти, где V — количество вершин в графе. В случае ненаправленного графа, эта матрица будет симметричной относительно главной диагонали. Несмотря на большие затраты памяти, она позволяет получать доступ к информации о наличии рёбер за O(1) времени, что выгодно при большом количестве запросов.

Note

Пусть граф G = (V, E) содержит N вершин и M рёбер.
Матрица смежности — это квадратная матрица A размера N × N, где элемент aᵢⱼ = 1, если существует ребро между вершинами i и j, и aᵢⱼ = 0 в противном случае.

Особенности:

• Подходит для плотных графов, у которых число рёбер порядка Θ(N²)
• Для ненаправленного графа матрица смежности всегда симметрична
• Память: 4 × N² байт
• Быстрое определение наличия ребра между вершинами i и j — доступ aᵢⱼ выполняется за O(1)
• Общий объём используемой памяти: O(V²)

Эффективно используется, когда |E| ≈ |V|².

Списки смежных вершин

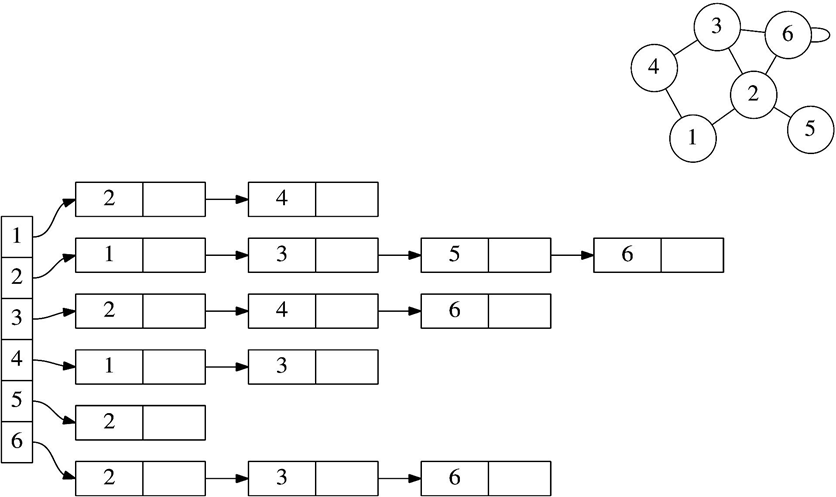
Второй способ — списки смежных вершин — представляет собой массив списков. Каждый элемент этого массива соответствует вершине графа и содержит перечень всех вершин, с которыми она соединена рёбрами.

Такой формат хранения значительно экономит память в случае разреженных графов, в которых количество рёбер значительно меньше максимального возможного. Он более гибок и позволяет эффективно выполнять обходы, такие как поиск в глубину и в ширину. При этом доступ к информации о наличии ребра требует перебора соответствующего списка, что может быть медленнее по сравнению с матрицей смежности.

Списки смежных вершин — это массив A[n], где каждый элемент A[i] содержит список всех вершин, смежных с вершиной i.

Особенности:

• Эффективны для разреженных графов, в которых |E| ≪ |V|²
• Требуют меньше памяти по сравнению с матрицей смежности
• Удобны при обходах графа (например, поиск в глубину или в ширину)

Используются, когда |E| ≈ |V|

Специализированные форматы хранения графов

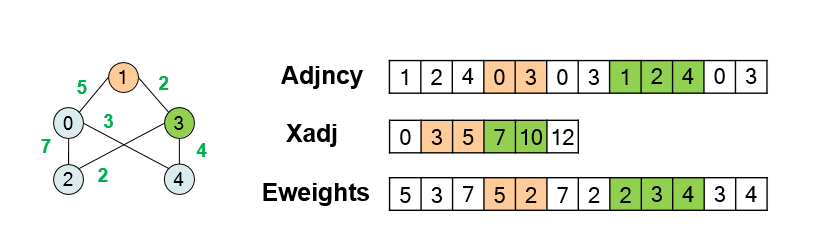
При работе с большими графами в инженерных и научных приложениях важно обеспечить эффективное хранение и быстрый доступ к структуре графа. Одним из популярных специализированных форматов хранения является формат CRS (Compressed Row Storage) — разновидность списков смежных вершин, заимствованная из методов хранения разреженных матриц.

Пусть граф G = (V, E) содержит N вершин и M рёбер. В формате CRS используется два основных массива:

• Adjncy — массив смежных вершин, хранящий последовательность всех соседей для каждой вершины. Вершины перечисляются подряд: сначала соседи вершины 0, затем вершины 1 и так далее. Размер массива — 2 * M, если граф ненаправленный.

• Xadj — массив индексов, указывающий, с какой позиции в Adjncy начинается список смежности очередной вершины. Для N вершин этот массив содержит N + 1 элемент. Последний элемент указывает на конец последнего списка.

Для получения всех соседей вершины i нужно обратиться к отрезку массива Adjncy от Xadj[i] до Xadj[i+1] - 1.

Такой способ экономит память и обеспечивает компактное хранение структуры графа, особенно эффективен для разреженных графов, где число рёбер примерно пропорционально числу вершин.

Если граф взвешенный, то дополнительно используется массив:

• Eweights — содержит веса рёбер в том же порядке, в каком рёбра перечислены в массиве Adjncy. Размер массива также 2 * M (для ненаправленного графа).

Полный объём требуемой памяти при использовании формата CRS составляет: 8 * M + 4 * N + 4 байт

где:
- 8 * M — массивы Adjncy и Eweights,
- 4 * N + 4 — массив Xadj.

Таким образом, CRS является оптимальным выбором для хранения разреженных графов, особенно если важна производительность при обходе или обработке соседей каждой вершины.

Распеделенный CRS

При хранении большого графа на /P/ процессах удобно использовать распределённый формат CRS (Compressed Row Storage). Он позволяет эффективно хранить и обрабатывать граф, распределяя вершины и рёбра между вычислительными узлами.

При хранении графа на /P/ процессах в формате CRS (Compressed Row Storage) используется следующая структура:

• Adjncy — массив всех соседей локальных вершин (аналогично обычному CRS).
• Xadj — массив индексов начала списков смежности в Adjncy для каждой локальной вершины.
• Нумерация вершин — с нуля (0-based indexing).

Дополнительно используется массив VertexDist размера /P + 1/, общий для всех процессов. Он описывает, какие вершины считаются локальными на каждом процессе:

• Для процесса /i/ локальными являются вершины с номерами от VertexDist[i] до VertexDist[i+1] – 1 включительно.
• Массив VertexDist хранится на каждом процессе.

Графическое представление:

Поиск в глубину в графе

Обход в глубину (DFS) — один из самых простых алгоритмов обхода графа. Входными параметрами для него являются граф и стартовая вершина. Алгоритм заключается в следующем:

1. Перебираем все рёбра, исходящие из стартовой вершины, и рекурсивно запускаем себя из каждой.
2. По окончании работы алгоритм обойдёт все вершины и рёбра, достижимые из стартовой вершины.
3. Ключевая деталь, делающая этот алгоритм быстрым, — пропуск уже посещённых вершин. Для этого вводится дополнительный массив из n булевых переменных, в которых хранится информация о том, посещал ли обход в глубину каждую вершину или нет.
4. Рекурсивные запуски будем производить только из тех вершин, которые ещё не помечены как посещённые.

Время работы алгоритма обхода в глубину зависит от способа представления графа. Однако важно отметить, что обход в глубину посещает каждую вершину не более одного раза, и при каждом посещении просматривает список исходящих рёбер только один раз.

Рассмотрим иллюстрацию:
Каждая вершина может находиться в одном из 3 состояний:

0 — оранжевый – необнаруженная вершина;
1 — зеленый – обнаруженная, но не посещенная вершина;
2 — серый – обработанная вершина;
Фиолетовый – рассматриваемая вершина.

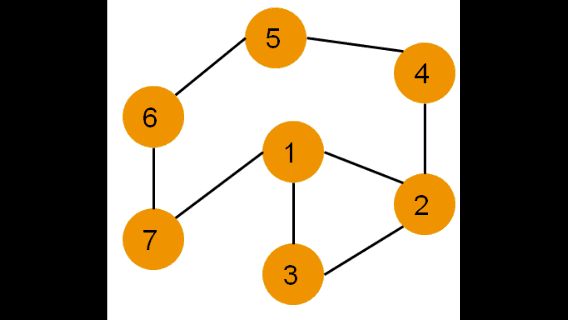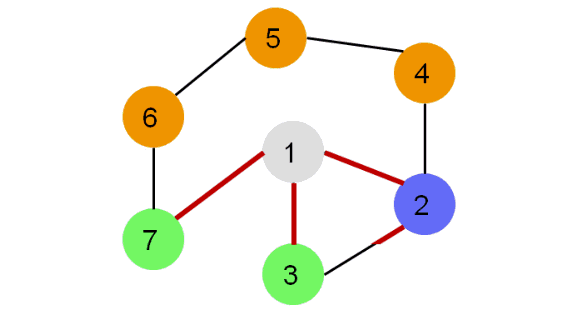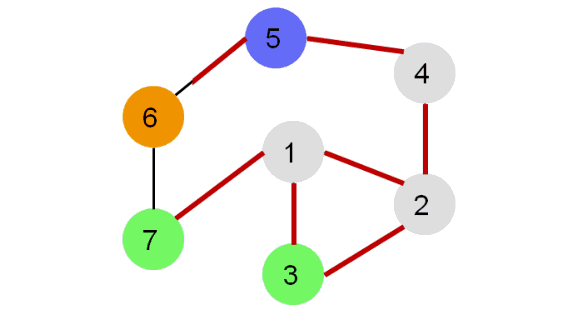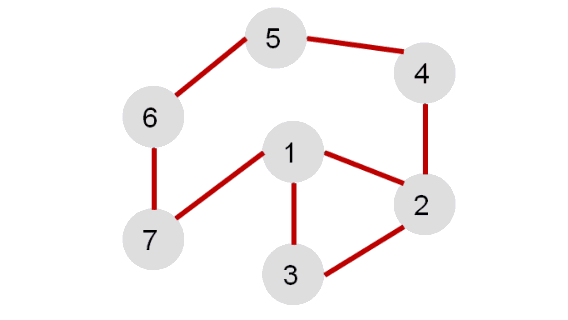
Для реализации алгоритма удобно использовать стек или рекурсию.

Реализация поиска в глубину

Обход в глубину на матрице смежности

PythonC++

def dfs(vertex):
    visited[vertex] = True  # Помечаем вершину как посещённую
    for to in range(vertex_count):  # Перебираем все вершины
        # Если есть ребро между текущей вершиной и вершиной to, и вершина to ещё не посещена
        if adj_matr[vertex][to] and not visited[to]:
            dfs(to)  # Рекурсивно вызываем dfs для вершины to

# Чтение количества вершин и рёбер
vertex_count, edge_count = map(int, input("Введите количество вершин и рёбер: ").split())

# Инициализация матрицы смежности
adj_matr = [[False] * vertex_count for _ in range(vertex_count)]

# Ввод рёбер и заполнение матрицы смежности
print("Введите рёбра (по одному на строку, с номерами вершин):")
for _ in range(edge_count):
    u, v = map(int, input().split())
    u -= 1  # Индексация с 0
    v -= 1  # Индексация с 0
    adj_matr[u][v] = True  # Заполняем матрицу смежности

# Массив для отслеживания посещённых вершин
visited = [False] * vertex_count

# Запуск DFS начиная с вершины 0 (вершина №1)
dfs(0)

# Вывод результатов
print("Вершины, которые были посещены:")
print(visited)  

#include <iostream>
#include <vector>

using namespace std;

// Рекурсивная функция для обхода в глубину
void dfs(int vertex, vector<vector<bool>>& adj_matr, vector<bool>& visited) {
    visited[vertex] = true;  // Помечаем вершину как посещённую
    for (int to = 0; to < adj_matr.size(); ++to) {  // Перебираем все вершины
        // Если есть ребро между текущей вершиной и вершиной to, и вершина to ещё не посещена
        if (adj_matr[vertex][to] && !visited[to]) {
            dfs(to, adj_matr, visited);  // Рекурсивно вызываем dfs для вершины to
        }
    }
}

int main() {
    int vertex_count, edge_count;

    // Чтение количества вершин и рёбер
    cout << "Введите количество вершин и рёбер: ";
    cin >> vertex_count >> edge_count;

    // Инициализация матрицы смежности
    vector<vector<bool>> adj_matr(vertex_count, vector<bool>(vertex_count, false));

    // Ввод рёбер и заполнение матрицы смежности
    cout << "Введите рёбра (по одному на строку, с номерами вершин):\n";
    for (int i = 0; i < edge_count; ++i) {
        int u, v;
        cin >> u >> v;
        u -= 1;  // Индексация с 0
        v -= 1;  // Индексация с 0
        adj_matr[u][v] = true;  // Заполняем матрицу смежности
    }

    // Массив для отслеживания посещённых вершин
    vector<bool> visited(vertex_count, false);

    // Запуск DFS начиная с вершины 0 (вершина №1)
    dfs(0, adj_matr, visited);

    // Вывод результатов
    cout << "Вершины, которые были посещены:\n";
    for (bool v : visited) {
        cout << (v ? "1" : "0") << " ";
    }
    cout << endl;

    return 0;
}

Обход в глубину на списках смежности

PythonC++

def dfs(vertex):
    visited[vertex] = True  # Помечаем вершину как посещённую
    for to in adj_list[vertex]:  # Перебираем соседей вершины
        if not visited[to]:  # Если сосед не посещён
            dfs(to)  # Рекурсивно вызываем dfs для этого соседа

# Чтение количества вершин и рёбер
vertex_count, edge_count = map(int, input("Введите количество вершин и рёбер: ").split())

# Инициализация списка смежности
adj_list = [[] for _ in range(vertex_count)]

# Ввод рёбер и заполнение списка смежности
print("Введите рёбра (по одному на строку, с номерами вершин):")
for _ in range(edge_count):
    u, v = map(int, input().split())
    u -= 1  # Индексация с 0
    v -= 1  # Индексация с 0
    adj_list[u].append(v)  # Добавляем ребро в список смежности

# Массив для отслеживания посещённых вершин
visited = [False] * vertex_count

# Запуск DFS начиная с вершины 0 (вершина №1)
dfs(0)

# Вывод результатов
print("Вершины, которые были посещены:")
print(visited)

#include <iostream>
#include <vector>

using namespace std;

// Функция для выполнения обхода в глубину
void dfs(int vertex, vector<bool>& visited, const vector<vector<int>>& adj_list) {
    visited[vertex] = true;  // Помечаем вершину как посещённую
    for (int to : adj_list[vertex]) {  // Перебираем соседей вершины
        if (!visited[to]) {  // Если сосед не посещён
            dfs(to, visited, adj_list);  // Рекурсивно вызываем dfs для этого соседа
        }
    }
}

int main() {
    int vertex_count, edge_count;

    // Чтение числа вершин и рёбер
    cout << "Введите количество вершин и рёбер: ";
    cin >> vertex_count >> edge_count;

    // Инициализация списка смежности
    vector<vector<int>> adj_list(vertex_count);

    // Ввод рёбер и заполнение списка смежности
    cout << "Введите рёбра (по одному на строку, с номерами вершин):\n";
    for (int i = 0; i < edge_count; ++i) {
        int u, v;
        cin >> u >> v;
        u -= 1;  // Индексация с 0
        v -= 1;  // Индексация с 0
        adj_list[u].push_back(v);  // Добавляем ребро в список смежности
    }

    // Массив для отслеживания посещённых вершин
    vector<bool> visited(vertex_count, false);

    // Запуск DFS начиная с вершины 0 (вершина №1)
    dfs(0, visited, adj_list);

    // Вывод результатов
    cout << "Вершины, которые были посещены:\n";
    for (bool is_visited : visited) {
        cout << is_visited << " ";
    }
    cout << endl;

    return 0;
}

Ограничение на глубину рекурсии

Обход в глубину (DFS) требует значительных ресурсов стека из-за рекурсивных вызовов. 
В худшем случае, если граф связан, глубина рекурсии может достичь числа вершин. В задачах с большим количеством вершин (сотни тысяч) это может привести к переполнению стека и аварийному завершению программы. 
В C++ с компилятором MSVC можно увеличить размер стека с помощью директивы #pragma, но в других случаях требуется использовать флаги тестирующей системы. В Python увеличение стека напрямую невозможно, что ограничивает использование DFS для больших графов.

Поиск в ширину в графе

Алгоритм обхода в ширину (англ. breadth-first search, или, сокращенно, BFS) действует таким образом, что он постепенно удаляется от стартовой вершины, двигаясь от неё по всевозможным направлениям.

Поиск в ширину (BFS) подразумевает поуровневое исследование графа:

1. Вначале посещается корень – произвольно выбранный узел.
2. Затем посещаются все потомки данного узла.
3. После этого посещаются потомки потомков и т.д.
4. Вершины просматриваются в порядке возрастания их расстояния от корня.
5. Алгоритм прекращает свою работу после обхода всех вершин графа или в случае выполнения требуемого условия (например, найти кратчайший путь из вершины 1 в вершину 6).

Каждая вершина может находиться в одном из 3 состояний:
- 0 — оранжевый: необнаруженная вершина.
- 1 — зеленый: обнаруженная, но не посещенная вершина.
- 2 — серый: обработанная вершина.
- Фиолетовый: рассматриваемая вершина.

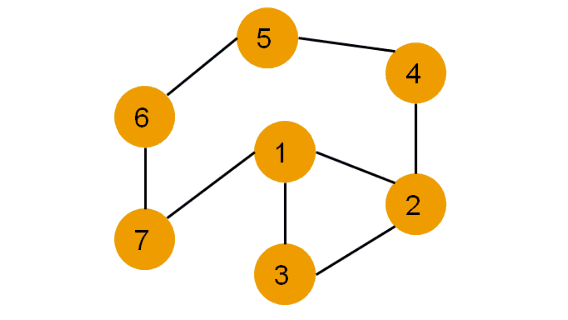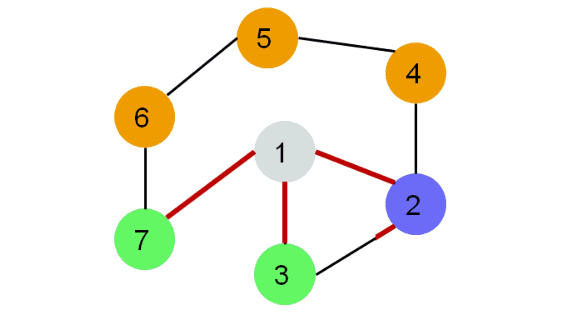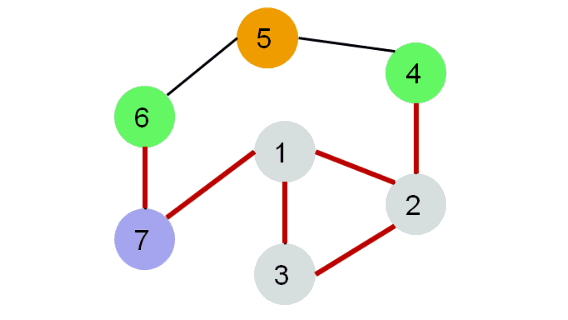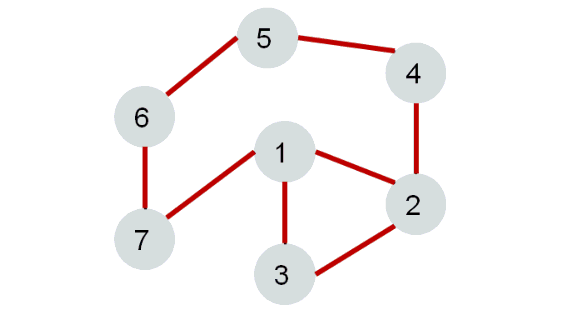
Реализация поиска в ширину

Обход в ширину на матрице смежности

PythonC++

from collections import deque

# Ввод количества вершин и рёбер
vertex_count, edge_count = map(int, input("Введите количество вершин и рёбер: ").split())

# Инициализация матрицы смежности
adj_matr = [[False] * vertex_count for _ in range(vertex_count)]

# Ввод рёбер и заполнение матрицы смежности
print("Введите рёбра (по одному на строку):")
for _ in range(edge_count):
    u, v = map(int, input().split())
    u -= 1  # Индексация с 0
    v -= 1  # Индексация с 0
    adj_matr[u][v] = True  # Ориентированный граф
    adj_matr[v][u] = True  # Для неориентированного графа

# Массив для хранения расстояний
dist = [None] * vertex_count

# Стартовая вершина (в Python индекс начинается с 0, так что вершина 1 - это индекс 0)
start = 0

# Инициализация очереди и расстояния для стартовой вершины
queue = deque()
queue.append(start)
dist[start] = 0

# Обход в ширину
while queue:
    vertex = queue.popleft()
    for to in range(vertex_count):
        if adj_matr[vertex][to] and dist[to] is None:
            queue.append(to)
            dist[to] = dist[vertex] + 1

# Вывод расстояний до всех вершин
print("Расстояния от стартовой вершины:")
for i in range(vertex_count):
    print(f"До вершины {i + 1}: {dist[i]}")

#include <iostream>
#include <vector>
#include <queue>

using namespace std;

int main() {
    int vertex_count, edge_count;
    cout << "Введите количество вершин и рёбер: ";
    cin >> vertex_count >> edge_count;

    // Инициализация матрицы смежности
    vector<vector<bool>> adj_matr(vertex_count, vector<bool>(vertex_count, false));

    // Ввод рёбер и заполнение матрицы смежности
    cout << "Введите рёбра (по одному на строку, с номерами вершин):\n";
    for (int i = 0; i < edge_count; i++) {
        int u, v;
        cin >> u >> v;
        u--;  // Индексация с 0
        v--;  // Индексация с 0
        adj_matr[u][v] = true;  // Ориентированный граф
        adj_matr[v][u] = true;  // Для неориентированного графа (если нужно)
    }

    // Массив для хранения расстояний
    vector<int> dist(vertex_count, -1);  // Изначально все вершины недостижимы

    // Стартовая вершина
    int start = 0;

    // Инициализация очереди и расстояния для стартовой вершины
    queue<int> q;
    q.push(start);
    dist[start] = 0;

    // Обход в ширину
    while (!q.empty()) {
        int vertex = q.front();
        q.pop();

        for (int to = 0; to < vertex_count; to++) {
            if (adj_matr[vertex][to] && dist[to] == -1) {  // Если вершина ещё не посещена
                q.push(to);
                dist[to] = dist[vertex] + 1;
            }
        }
    }

    // Вывод расстояний до всех вершин
    cout << "Расстояния от стартовой вершины:\n";
    for (int i = 0; i < vertex_count; i++) {
        cout << "До вершины " << i + 1 << ": " << dist[i] << endl;
    }

    return 0;
}

Обход в ширину на списках смежности

PythonC++

from collections import deque

# Ввод числа вершин и рёбер
vertex_count, edge_count = map(int, input("Введите количество вершин и рёбер: ").split())

# Инициализация списка смежности
adj_list = [[] for _ in range(vertex_count)]

# Ввод рёбер
print("Введите рёбра (по одному на строку):")
for _ in range(edge_count):
    u, v = map(int, input().split())
    u -= 1  # Индексация с 0
    v -= 1  # Индексация с 0
    adj_list[u].append(v)
    adj_list[v].append(u)  # Если граф неориентированный

# Инициализация массива расстояний
dist = [None] * vertex_count

# Выбор стартовой вершины (например, вершина 0)
start = 0

# Инициализация очереди и расстояния для стартовой вершины
queue = deque([start])
dist[start] = 0

# Обход в ширину
while queue:
    vertex = queue.popleft()
    for to in adj_list[vertex]:
        if dist[to] is None:  # Если вершина ещё не посещена
            queue.append(to)
            dist[to] = dist[vertex] + 1  # Расстояние до вершины

# Вывод расстояний до всех вершин
print("Расстояния от стартовой вершины:")
print(dist)

#include <iostream>
#include <vector>
#include <queue>

using namespace std;

int main() {
    int vertex_count, edge_count;

    // Ввод числа вершин и рёбер
    cout << "Введите количество вершин и рёбер: ";
    cin >> vertex_count >> edge_count;

    // Инициализация списка смежности
    vector<vector<int>> adj_list(vertex_count);

    // Ввод рёбер
    cout << "Введите рёбра (по одному на строку):\n";
    for (int i = 0; i < edge_count; ++i) {
        int u, v;
        cin >> u >> v;
        u -= 1;  // Индексация с 0
        v -= 1;  // Индексация с 0
        adj_list[u].push_back(v);
        adj_list[v].push_back(u);  // Если граф неориентированный
    }

    // Массив для хранения расстояний
    vector<int> dist(vertex_count, -1);

    // Стартовая вершина
    int start = 0;

    // Инициализация очереди и расстояния для стартовой вершины
    queue<int> q;
    q.push(start);
    dist[start] = 0;

    // Обход в ширину
    while (!q.empty()) {
        int vertex = q.front();
        q.pop();

        for (int to : adj_list[vertex]) {
            if (dist[to] == -1) {  // Если вершина ещё не посещена
                q.push(to);
                dist[to] = dist[vertex] + 1;  // Расстояние до вершины
            }
        }
    }

    // Вывод расстояний до всех вершин
    cout << "Расстояния от стартовой вершины:\n";
    for (int i = 0; i < vertex_count; ++i) {
        cout << "До вершины " << i + 1 << ": " << dist[i] << endl;
    }

    return 0;
}

Время работы обхода в ширину при использовании списков смежности составляет О(п + m), где п — число вершин, m — число ребер, поскольку в худшем случае обход в ширину обработает каждую вершину и пройдет по всем спискам смежности.