Оценка эффективности параллельных вычислений

Презентация Лекция 6
При разработке параллельных алгоритмов решения сложных научно-технических задач важным моментом является анализ эффективности использования параллелизма, который заключается в оценке ускорения процесса вычислений (сокращения времени решения задачи).

Оценка эффективности параллельных вычислений может быть проведена двумя подходами:
- оценка распараллеливания конкретного алгоритма
- оценка максимально возможного ускорения

Для точной оценки параллельности используется модель вычислений в виде графа "операции-операнды", которая позволяет описать существующие информационные зависимости между операциями и представить вычислительный процесс.

Эти методы дают возможность оценить максимально возможный параллелизм, что помогает определить пределы возможного ускорения при оптимальном использовании параллельных вычислений.

Модель вычислений в виде графа "операции-операнды"

Для описания информационных зависимостей в алгоритмах решения задач используется модель в виде графа "операции-операнды" (см., например, Bertsekas and Tsitsiklis (1989), Воеводин В.В. и Воеводин Вл.В. (2002)). При этом предполагается, что время выполнения любых вычислительных операций одинаково и равно 1 (в тех или иных единицах измерения), а передача данных между вычислительными устройствами осуществляется мгновенно, без затрат времени. Это предположение может быть справедливо, например, в системах с общей разделяемой памятью.

Ациклический ориентированный граф

Предположим, что множество операций, выполняемых в исследуемом алгоритме, и информационные зависимости между ними могут быть представлены в виде ациклического ориентированного графа:

$$G = (V, R)$$

где $V = \{1, \dots, V\}$ — множество вершин графа, представляющих выполняемые операции алгоритма, а $R$ — множество дуг графа, где дуга $r = (i, j)$ принадлежит графу, только если операция $i$ использует результат выполнения операции $j$.

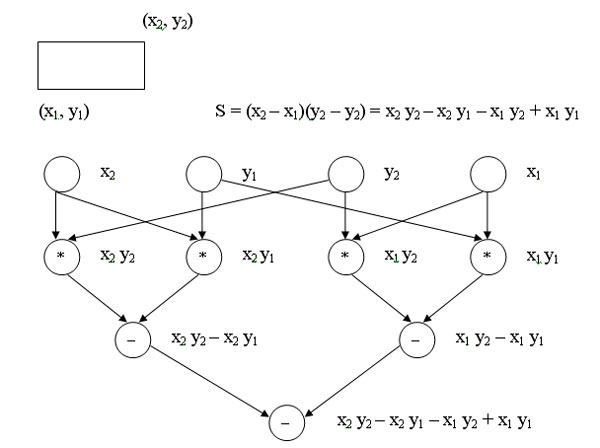
Пример: граф алгоритма вычисления площади прямоугольника, заданного координатами двух противоположных углов. В данном случае различные схемы вычислений могут быть использованы для решения задачи, и для каждой из них будет построена своя вычислительная модель.

Выбор наиболее подходящей схемы

В процессе разработки алгоритма для параллельных вычислений можно выбрать наиболее подходящую вычислительную схему, которая обеспечит наибольшее распараллеливание.

Роль вершин графа

В рассматриваемой модели алгоритма вершины без входных дуг могут использоваться для задания операций ввода, а вершины без выходных дуг — для операций вывода. Также определяется диаметр графа, который представляет собой длину максимального пути в графе и является важной характеристикой для анализа параллелизма.

Описание схемы параллельного выполнения алгоритм

Операции алгоритма, между которыми нет зависимостей (нет пути в графе), могут быть выполнены параллельно. Например, для вычислительной схемы на рисунке 1, представленной ранее, можно параллельно выполнить все операции умножения, а затем первые две операции вычитания.

Для описания параллельного выполнения алгоритма используется понятие расписания операций. Пусть $p$ — количество процессоров, используемых для выполнения алгоритма. Тогда для параллельного выполнения вычислений необходимо задать множество $H_p = \{(i, P_i, t_i): i \in V\}$, где для каждой операции $i$, принадлежащей множеству вершин $V$, указывается номер процессора $P_i$ и время начала выполнения операции $t_i$.

Для реализации расписания необходимо выполнить два основных требования:

1. Уникальность процессора: Для любых $i$ и $j$, принадлежащих $V$, если $t_i = t_j$, то $P_i \neq P_j$, то есть один и тот же процессор не должен назначаться разным операциям в один и тот же момент времени.

2. Учет зависимостей: Для всех пар $(i,j)$, принадлежащих $R$, должно выполняться условие $t_j \ge t_i + 1$, то есть операция $j$ не может быть запущена до того, как будут выполнены все необходимые операции для её вычисления.

При запуске программы на распределенной памяти указывается название программы и количество процессоров, которое требуется выделить. После запуска программы выделяется некоторое количество процессорных узлов, которые могут совпадать или не совпадать с запрашиваемым количеством. На каждом процессоре запускается своя копия программы, и у каждой копии программы будет своя оперативная память. Разные копии программы, запущенные на разных процессорных узлах, не могут взаимодействовать с внутренними переменными других копий.

Каждая копия программы получает два параметра: число процессоров, которое было запрошено, и номер процессора. Обмен данными между копиями программы осуществляется с использованием номера процессора-получателя.

При запуске программы на общей памяти фактически запускается только одна копия программы. Когда требуется задействовать другие процессоры системы, выполняется вызов функции для порождения дополнительной нити. Эти вычисления будут выполняться в параллельном потоке. Число нитей может быть равно числу процессоров в системе, или больше, чем число процессоров, в этом случае часть нитей будет работать в конкурентном режиме (режим разделения времени).

Каждая нить получает свой стек и имеет свои локальные переменные, но все нити имеют общий доступ к глобальным переменным.

Определение времени выполнения параллельного алгоритма

Вычислительная схема алгоритма совместно с расписанием может быть рассмотрена как модель параллельного алгоритма, который выполняется с использованием процессоров. Время выполнения параллельного алгоритма определяется максимальным значением времени, использующимся в расписании:

$$T_p(G, H_p) = \max_{i \in V} \left(t_i + 1 \right)$$

где $t_i$ — время начала выполнения операции $i$, а $V$ — множество всех вершин графа, представляющих операции.

Для выбранной схемы вычислений целью является использование расписания, которое обеспечит минимальное время выполнения алгоритма:

$$T_p(G, H_p) = \min T_p(G, H_p)$$

Уменьшение времени выполнения может быть достигнуто путем выбора наилучшей вычислительной схемы:

$$T_{min}(G) = \min T_p(G)$$

Оценки $T_p(G, H_p)$ и $T_{min}(G)$ могут быть использованы в качестве показателей времени выполнения параллельного алгоритма.

Оценка максимально возможного параллелизма

Для анализа максимально возможного параллелизма можно определить оценку наиболее быстрого исполнения алгоритма:

$$T_{\infty}(G, H_p) = \min \left(T_1(G) \geq T_p \right)$$

Оценка $T_{\infty}$ представляет собой минимально возможное время выполнения параллельного алгоритма при использовании неограниченного числа процессоров. Это концепция паракомпьютера, широко используемая при теоретическом анализе параллельных вычислений.

Оценка последовательного времени выполнения

Оценка $T_1(G)$ представляет время выполнения последовательного варианта алгоритма. Это важная задача для анализа параллельных алгоритмов, поскольку она необходима для определения эффекта использования параллелизма (ускорения времени решения задачи).

$$T_1(G) = V$$

где $V$ — количество вершин в вычислительной схеме без вершин ввода.

Если при определении оценки использовать только выбранный алгоритм решения задачи и величину $T_1(G)$, то показатели ускорения будут характеризовать эффективность распараллеливания конкретного алгоритма.

Для оценки эффективности параллельного решения задачи следует учитывать различные последовательные алгоритмы и использовать величину:

$$T_1^* = \min T_1$$

где операция минимума берется по множеству всех возможных последовательных алгоритмов решения задачи.

Показатели эффективности параллельного алгоритма

Ускорение (Speedup)

Ускорение, которое достигается при использовании параллельного алгоритма для $p$ процессоров, по сравнению с последовательным вариантом вычислений, определяется величиной:

$$S(n, p) = \frac{T(n)}{T_p(n)}$$

где $T(n)$ — время выполнения последовательного алгоритма, а $T_p(n)$ — время выполнения параллельного алгоритма с $p$ процессорами. Ускорение используется для параметризации вычислительной сложности задачи и может быть интерпретировано, например, как количество входных данных задачи.

Эффективность (Efficiency)

Эффективность использования параллельных процессоров при решении задачи определяется соотношением:

$$E(n, p) = \frac{S(n, p)}{p} = \frac{T(n)}{p T_p(n)}$$

Эффективность определяет среднюю долю времени, в течение которой процессоры реально используются для решения задачи.

Сверхлинейное ускорение

При определённых обстоятельствах ускорение может превышать число процессоров, в этом случае говорят о сверхлинейном ускорении. Хотя это явление может казаться парадоксальным, оно может иметь место на практике. Причины сверхлинейного ускорения могут быть следующими:

1. Неравноправность выполнения последовательной и параллельной программ: при решении задачи на одном процессоре может не хватить оперативной памяти для хранения всех данных, и необходимым становится использование более медленной внешней памяти. При использовании нескольких процессоров оперативная память может быть разделена между ними, что улучшает ситуацию.

2. Нелинейный характер зависимости сложности задачи от объема обрабатываемых данных: например, алгоритм пузырьковой сортировки имеет квадратичную зависимость от числа упорядочиваемых элементов, что может привести к ускорению, превышающему число процессоров при распределении данных.

3. Различие в вычислительных схемах последовательных и параллельных методов: в некоторых случаях различия в способах вычислений могут привести к ускорению, которое превышает число процессоров.

Противоречие между ускорением и эффективностью

Попытки улучшить один из показателей качества параллельных вычислений (ускорение или эффективность) могут привести к ухудшению другого. Например:

• Повышение ускорения часто достигается за счёт увеличения числа процессоров, что обычно ведет к снижению эффективности.
• Повышение эффективности достигается при уменьшении числа процессоров, и идеальная эффективность ($E(n) = 1$) может быть достигнута при использовании одного процессора.

Как результат, разработка методов параллельных вычислений часто требует выбора компромиссного варианта, учитывая желаемые показатели ускорения и эффективности.

Стоимость вычислений

Стоимость вычислений может быть определена как произведение времени параллельного решения задачи на число используемых процессоров:

$$C = p \cdot T_p$$

Стоимостно-оптимальный (cost-optimal) параллельный алгоритм — это метод, стоимость которого пропорциональна времени выполнения наилучшего последовательного алгоритма.

В следующем пункте будет рассмотрен учебный пример решения задачи вычисления частных сумм для последовательности числовых значений, где будут использованы эти показатели для характеристики эффективности рассматриваемых параллельных алгоритмов.

Оценка максимально достижимого параллелизма

Оценка качества параллельных вычислений предполагает знание наилучших (максимально достижимых) значений показателей ускорения и эффективности. Однако идеальные величины, такие как $S_p = p$ для ускорения и $E_p = 1$ для эффективности, могут быть недостижимы для всех вычислительно трудоемких задач.

Для рассматриваемого учебного примера минимально достижимое время параллельного вычисления суммы числовых значений составляет $\log_2 n$, что ограничивает максимально возможное ускорение. Теоретические утверждения, приведенные в начале раздела, оказывают содействие в решении данной проблемы, однако следует рассмотреть и дополнительные закономерности.

Закон Амдала

Закон Амдала описывает проблему, когда достижению максимального ускорения может препятствовать существование последовательных вычислений, которые не могут быть распараллелены. Пусть $f$ — доля последовательных вычислений в алгоритме. Согласно закону Амдала, ускорение процесса вычислений при использовании $p$ процессоров ограничено следующим выражением:

$$S_p \leq \frac{1}{f + \frac{1 - f}{p}}$$

где $f$ — доля последовательных вычислений, а $p$ — количество процессоров.

Так, например, если доля последовательных команд в алгоритме составляет всего 10% ($f = 0.1$), то эффект использования параллелизма не может превышать 10-кратного ускорения. Для вычисления суммы значений в каскадной схеме доля последовательных расчетов составляет $f = \frac{\log_2 n}{n}$, и как результат, величина возможного ускорения ограничена оценкой:

$$S_n \leq \frac{n}{\log_2 n}$$

Графическое изображение закона Амдала

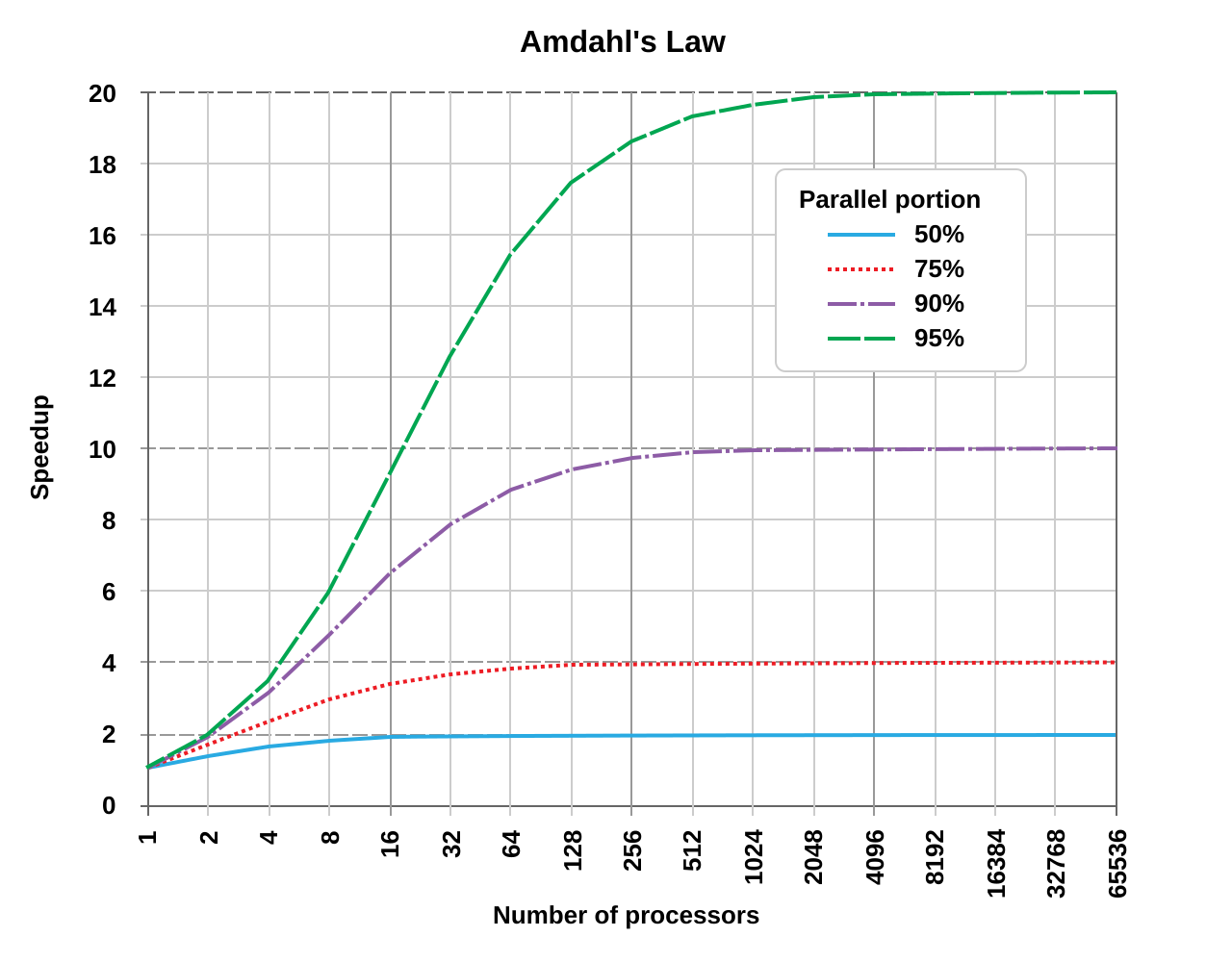
Закон Амдала подчеркивает одну из самых серьезных проблем в области параллельного программирования: алгоритмы с определенной долей последовательных команд практически не существуют. Однако доля последовательных вычислений часто зависит от характеристик самого алгоритма, а не от параллельности решения задачи. Таким образом, можно значительно уменьшить долю последовательных вычислений при выборе более подходящих методов для распараллеливания.

Следует также отметить, что закон Амдала предполагает, что доля последовательных расчетов $f$ является постоянной величиной и не зависит от параметра $n$, определяющего вычислительную сложность задачи. Однако для ряда задач доля последовательных вычислений может быть функцией от $n$, то есть $f = f(n)$, и в этом случае ускорение для фиксированного числа процессоров может увеличиваться с ростом вычислительной сложности задачи.

Это наблюдение приводит к утверждению, что ускорение $S_p = S_p(n)$ является возрастающей функцией от параметра $n$. Это явление часто называют эффектом Амдаля, который показывает, как увеличение размера задачи может повысить эффективность использования параллелизма.

Пример

Давайте предположим, что у нас имеется некая вычислительная программа и к ней применимо следующее:

40% её содержимого является предметом для параллельного исполнения, следовательно $B = 1 - 40\% = 0.6$.

Её параллельные части будут обрабатываться четырьмя процессорами, поэтому $j = 4$.

Закон Амдала постулирует, что общее ускорение применения улучшения будет таким:

$$S = \frac{1}{B + \frac{1 - B}{j}} = \frac{1}{0.6 + \frac{1 - 0.6}{4}} = \frac{10}{7} \approx 1.43$$

Следствия закона Амдала

Цитата Джина Амдала, 1967:

Уже более десяти лет высказывается мнение, что организация единого компьютера достигла своих пределов и что действительно значительные успехи могут быть достигнуты лишь путём объединения множества компьютеров таким образом, чтобы обеспечить совместное решение... Основу природы таких вряд ли поддаются методам параллельной обработки издержек (при параллельной обработке), по всей видимости, являются последовательные вычисления, которые накладные расходы сами по себе установили бы некий предел пропускной способности, который бы в пять-семь раз превышал бы скорость последовательной обработки, даже если бы все служебные операции выполнялись бы в отдельном процессоре... Трудно предсказать в любой момент времени как будут преодолены узкие места последовательного вычисления.

Согласно этой цитате Амдал указывает, что всякий раз, когда мы реализуем в какой-либо программе совместные и параллельные методы обработки, присущая ей последовательная часть накладных расходов всегда устанавливает некую верхнюю границу того, насколько можно разогнать эту программу. Именно это является одним из следствий, которые далее предлагает Закон Амдала.

Рассмотрим следующий пример:

$$\frac{1 - B}{j} > \frac{1 - B}{j + 1} \Rightarrow \frac{1}{B + \frac{1 - B}{j}} < \frac{1}{B + \frac{1 - B}{j + 1}} \Rightarrow S_j < S_{j+1}$$

$S_n$ — это ускорение, получаемое $n$ процессорами.

Это показывает, что по мере роста числа ресурсов (в частности, общего числа доступных процессоров), значение ускорения всей задачи целиком также возрастает. Тем не менее, это вовсе не означает, что для достижения наивысшей производительности мы должны всегда реализовывать совместную обработку и параллелизм настолько большим числом процессоров, насколько это возможно. На самом деле, из этой формулы мы также можем уловить, что значение ускорения, достигаемого от последовательного увеличения процессоров, падает. Другими словами, по мере того как мы добавляем дополнительные процессоры для своей программы одновременной обработки, мы будем получать всё меньше и меньше улучшений во времени исполнения.

Более того, как уже упоминалось ранее, другим следствием, которое предсказывает Закон Амдала, является наличие значения верхнего предела для величины улучшения времени исполнения:

$$\begin{cases} S \leq \frac{1}{B} \\ \lim_{j \to \infty} S = \frac{1}{B} \end{cases}$$

Это является верхним пределом того, насколько совместная обработка и параллелизм могут улучшить вашу программу. Это означает, что вне зависимости от того, сколько у вашей системы в доступности ресурсов, невозможно получить ускорение выше, нежели оно достигается совместной обработкой, и этот предел диктуется накладными расходами имеющейся в программе последовательной части ($B$ — это та часть вашей программы, которая является жёстко последовательной).

Закон Густавсона - Барсиса

Закон Густавсона-Барасиса оценивает максимально достижимое ускорение с учетом доли последовательных расчетов в параллельных вычислениях. Для вычислений с долей последовательной работы $g$, время выполнения задачи на $p$ процессорах можно выразить как:

$$T(n, p) = \tau(n) + \frac{\pi(n)}{p}$$

где $\tau(n)$ и $\pi(n)$ — времена последовательной и параллельной частей соответственно.

Вводимая величина $g$ позволяет выразить:

$$\tau(n) = g \cdot \left( \tau(n) + \frac{\pi(n)}{p} \right)$$

$$\pi(n) = (1 - g) \cdot p \cdot \left( \tau(n) + \frac{\pi(n)}{p} \right)$$

Ускорение можно оценить через:

$$S(p) = \frac{T(1)}{T(p)} = \frac{\tau(n) + \pi(n)}{\tau(n) + \frac{\pi(n)}{p}}$$

И после упрощения получаем закон Густавсона-Барасиса:

$$S(p) = g + (1 - g) \cdot p$$

Теперь мы ввели достаточно теоретический понятий и нам необходимо некоторая практика. Рассмотрим на примере Python наше ускорение.

Global Interpreter Lock (GIL)

CPython — популярная реализация интерпретатора Python — имеет встроенный механизм, который обеспечивает выполнение ровно одного потока в любой момент времени.

GIL облегчает реализацию интерпретатора, защищая объекты от одновременного доступа из нескольких потоков.
Поэтому создание нескольких потоков не приведёт к их одновременному исполнению на разных ядрах процессора.

Однако, некоторые модули, как стандартные, так и сторонние, созданы для освобождения GIL при выполнении тяжелых вычислительных операций (например, сжатие или хеширование). К тому же, GIL всегда свободен при выполнении операций ввода-вывода.

Неформальное определение GIL

Питон слывёт дружелюбным и простым в общении, но есть у него причуды. Нельзя просто взять и воспользоваться всеми преимуществами многопоточности в Python! Дорогу вам преградит огромный шлюз… Даже так — глобальный шлюз (Global Interpreter Lock, он же GIL), который ограничивает многопоточность на уровне интерпретатора.

Технически, это один на всех mutex, созданный по умолчанию. Такого нет ни в C, ни в Java.

Note

Задача шлюза — пропускать потоки строго по одному, чтоб не летали наперегонки, как печально известные стритрейсеры, и не создавали угрозу работе интерпретатора.

Без GIL потоки подрезали бы друг друга, чтобы первыми добраться до памяти, но это еще не всё. Они имеют обыкновение внезапно засыпать за рулём! Операционная система не спрашивает, вовремя или невовремя — просто усыпляет их в ей одной известный момент.

Из-за этого неупорядоченные потоки могут неожиданно перехватывать друг у друга инициативу в работе с общими ресурсами.

Дезориентированный спросонок поток, который видит перед собой совсем не ту ситуацию, при которой засыпал, рискует разбиться и повалить интерпретатор, либо попасть в тупиковую ситуацию (deadlock).
Пример:
Перед сном Поток 1 начал работу со списком, а после пробуждения не нашёл в этом списке элементов, т.к. их удалил или перезаписал Поток 2..

Чтобы такого не было, GIL в предсказуемый момент (по умолчанию раз в 5 миллисекунд для Python 3.2+) командует отработавшему потоку:

«СПАААТЬ!»

Тот отключается и не мешает проезжать следующему желающему.
Даже если желающего нет, блокировщик всё равно подождёт, прежде чем вернуться к предыдущему активному потоку.

✅ Благодаря GIL однопоточные приложения работают быстро, а потоки не конфликтуют.
❌ Но многопоточные программы при таком подходе выполняются медленнее — слишком много времени уходит на регулировку «дорожного движения».

А значит обработка графики, расчет математических моделей и поиск по большим массивам данных c GIL идут неприемлемо долго.

В статье «Understanding Python GIL» технический директор компании Gaglers Inc. и разработчик со стажем Chetan Giridhar приводит такой пример:

from datetime import datetime
import threading
def factorial(number): 
    fact = 1
    for n in range(1, number+1): 
        fact *= n 
    return fact 
number = 100000 
thread = threading.Thread(target=factorial, args=(number,)) 
startTime = datetime.now() 
thread.start() 
thread.join()

endTime = datetime.now() 
print "Время выполнения: ", endTime - startTime

Код вычисляет факториал числа 100 000 и показывает, сколько времени ушло у машины на эту задачу.
При тестировании на одном ядре и с одним потоком вычисления заняли 3,4 секунды.

Тогда Четан создал и запустил второй поток.
Результат? Расчёт факториала на двух ядрах длился 6,2 секунды.

А ведь по логике скорость вычислений не должна была существенно измениться!

Повторите этот эксперимент на своей машине и посмотрите, насколько медленнее будет решена задача, если вы добавите thread2.
Я получила замедление ровно вдвое.

Глобальный шлюз — наследие времён, когда программисты боролись за достойную реализацию многозадачности, и у них не очень получалось.

Но зачем он сегодня, когда есть много- и очень многоядерные процессоры?

Как объяснил Гвидо ван Россум:
- Без GIL не будут нормально работать C-расширения для Python.
- Производительность однопоточных приложений упадёт:
- Python 3 станет медленнее, чем Python 2.
- А это никому не нужно.

Эксперимент

Напишем простую программу, которая будет находить сумму чисел массива с использованием N потоков. Запустить с разным параметром N. Убедиться, что несмотря на увеличение N, ускорения подсчета не происходит. Причина этому - GIL. В Python вычисления распараллеливать бессмысленно. Замерить время работы можно с помощью библиотеки time (ответ в секундах):

import threading
import time
import random

# Функция для вычисления суммы части массива
def partial_sum(arr, result, index):
    result[index] = sum(arr)

# Основная функция
def parallel_sum(arr, num_threads):
    chunk_size = len(arr) // num_threads
    threads = []
    results = [0] * num_threads  # Массив для хранения частичных сумм

    for i in range(num_threads):
        start = i * chunk_size
        end = len(arr) if i == num_threads - 1 else (i + 1) * chunk_size
        thread = threading.Thread(target=partial_sum, args=(arr[start:end], results, i))
        threads.append(thread)
        thread.start()

    for thread in threads:
        thread.join()

    return sum(results)

if __name__ == "__main__":
    N_values = [1, 2, 4, 8, 16]  # Различное количество потоков
    array = [random.randint(1, 100) for _ in range(10**6)]  # Генерируем массив

    for N in N_values:
        start_time = time.time()
        result = parallel_sum(array, N)
        elapsed_time = time.time() - start_time
        print(f"N = {N}, Sum = {result}, Time = {elapsed_time:.5f} sec")

Примерные результаты:

N = 1, Sum = 50487466, Time = 0.00600 sec
N = 2, Sum = 50487466, Time = 0.00500 sec
N = 4, Sum = 50487466, Time = 0.00600 sec
N = 8, Sum = 50487466, Time = 0.00702 sec
N = 16, Sum = 50487466, Time = 0.00775 sec

Обход блокировки GIL

Шлюз можно временно отключить. Для этого интерпретатор Python нужно отвлечь вызовом функции из внешней библиотеки или обращением к операционной системе. Например, шлюз выключится на время сохранения или открытия файла.

Помните наш пример с записью строк в файлы? Как только вызванная функция возвратит управление коду Python или интерфейсу Python C API, GIL снова включается.

Если вы хотите использовать Python для параллельных вычислений, можно воспользоваться процессами, которые работают изолированно и не подвержены влиянию GIL. Однако это уже большая отдельная тема, требующая более детального рассмотрения.

Библиотека multiprocessing

Библиотека multiprocessing позволяет организовать параллелизм вычислений за счет создания подпроцессов. Т.к. каждый процесс выполняется независимо от других, этот метод параллелизма позволяет избежать проблем с GIL.
Предоставляемый библиотекой API схож с тем, что есть в threading, хотя есть уникальные вещи. Создание процесса происходит поутем создания объекта класса Process. Аргументы конструктора аналогичны тем, что есть в конструкторе Thread. В том числе аргумент daemon позволяет создавать служебные процессы. Служебные процессы завершаются вместе с родительским процессом и не могут порождать свои подпроцессы.

Эксперимент

import multiprocessing
import time
import random

def partial_sum(arr):
    return sum(arr)

def parallel_sum(arr, num_processes):
    chunk_size = len(arr) // num_processes
    chunks = [arr[i * chunk_size : (i + 1) * chunk_size] for i in range(num_processes)]

    with multiprocessing.Pool(num_processes) as pool:
        results = pool.map(partial_sum, chunks)

    return sum(results)

if __name__ == "__main__":
    N_values = [1, 2, 4, 8, 16]
    array = [random.randint(1, 100) for _ in range(10**7)]  # Увеличенный массив

    for N in N_values:
        start_time = time.time()
        result = parallel_sum(array, N)
        elapsed_time = time.time() - start_time
        print(f"N = {N}, Sum = {result}, Time = {elapsed_time:.5f} sec")

N = 1, Sum = 505103360, Time = 0.36813 sec
N = 2, Sum = 505103360, Time = 0.22449 sec
N = 4, Sum = 505103360, Time = 0.20345 sec
N = 8, Sum = 505103360, Time = 0.20628 sec
N = 16, Sum = 505103360, Time = 0.25615 sec

Warning

Старайтесь не забывать про конструкцию __name__ == '__main__'. Это надо для того, чтобы ваш модуль можно было безопасно подключать в другие модули и при этом не создавались новые процессы без вашего ведома

Решения для многопоточности

Для сложных научных расчётов в Python существует несколько библиотек, которые помогают обойти проблемы с производительностью из-за GIL:

• Numba: ускоряет вычисления с помощью JIT-компиляции.
• NumPy: используется для научных вычислений и эффективно работает с многомерными массивами.
• SciPy: библиотеки для научных и технических вычислений.

Эти библиотеки помогают значительно улучшить производительность, поскольку они освобождают GIL для тяжёлых вычислений.

Я расскажу немного о каждой из них, чтобы вы могли решить, стоит ли разведывать это направление дальше.

Numba для математики

Numba — динамически, «на лету» компилирует Python-код, превращая его в машинный код для исполнения на CPU и GPU. Такая технология компиляции называется JIT — “Just in time”. Она помогает оптимизировать производительность программ за счет ускорения работы циклов и компиляции функций при первом запуске.

Суть в том, что вы ставите аннотации (декораторы) в узких местах кода, где вам нужно ускорить работу функций.

Для математических расчётов библиотеку удобно использовать в связке c NumPy. Допустим, нужно сложить одномерные массивы — элемент за элементом.

def arr_sum (x , y): 
    result_arr = nupmy.empty_like ( x)
    for i in range (len (x)) : 
    result_arr [i ] = x[i ] + y[i ] 
    return result_arr

Метод nupmy.empty_like() принимает массив и возвращает (но не инициализирует!) другой — соответствующий исходному по форме и типу. Чтобы ускорить выполнение кода, импортируем класс jit из модуля numba и добавляем в начало кода аннотацию @jit:

from numba import jit
@jit
def arr_sum(x,y):

Это скромное дополнение способно ускорить выполнение операции более чем в 100 раз! Если интересно, посмотрите замеры скорости математических расчётов при использовании разных библиотек для Python.

PyCUDA и Numba для графики

В графических вычислениях Numba тоже кое-что может. Она умеет работать с программной моделью CUDA, чтобы визуализировать научные данные и работу алгоритмов, выдавать информацию о GPU и др. Подробнее о том, как работают графический процессор и CUDA — здесь. И снова мы встретимся с многопоточностью.

При работе с многомерными массивами в CUDA, чтобы понять, какой поток сейчас работает с элементами массива, нужно отследить, кто и когда вызывает функцию ядра. Например, поток может определять свою позицию в сетке блоков и рассчитать соответствующий элемент массива:

from numba import cuda
@cuda.jit
def call_for_kernel(io_arr):
    # Идентификатор потока в одномерном блоке
    thread_x = cuda.threadIdx.x
    # Идентификатор блока в одномерной сетке
    thread_y = cuda.blockIdx.x
    # Число потоков на блок (т.е. ширина блока)
    block_width = cuda.blockDim.x
    # Находим положение в массиве
    t_position = thread_x + thread_y * block_width
    if  t_position < io_arr.size:  # Убеждаемся, что не вышли за границы массива
        io_arr[ t_position] *= 2 # Считаем

Главный плюс этого кода даже не в скорости исполнения, а в прозрачности и простоте. Снова сошлюсь на Хабр, где есть сравнение скорости GPU-расчетов при использовании Numba, PyCUDA и эталонного С CUDA[1]. Небольшой спойлер: PyCUDA позволяет достичь скорости вычислений, сопоставимой с Cи, а Numba подходит для небольших задач.

Практические приложения закона Амдала

Вернемся к нашему примеру с параллеьной обработкой суммы массива. Допустим, N - количество процессов, а p - время работы парралельного кода от общего времени работы программы в %, тогда теоретически рассчитаем следующеее

Параллельная часть (p)	Количество процессоров (N)	Ускорение (Speedup)
0.5	2	1.33
	4	1.60
	8	1.77
	16	1.88
	32	1.94
0.75	2	1.60
	4	2.29
	8	2.91
	16	3.37
	32	3.66
0.9	2	1.82
	4	3.08
	8	4.71
	16	6.40
	32	7.81
0.95	2	1.90
	4	3.47
	8	5.93
	16	9.14
	32	12.54

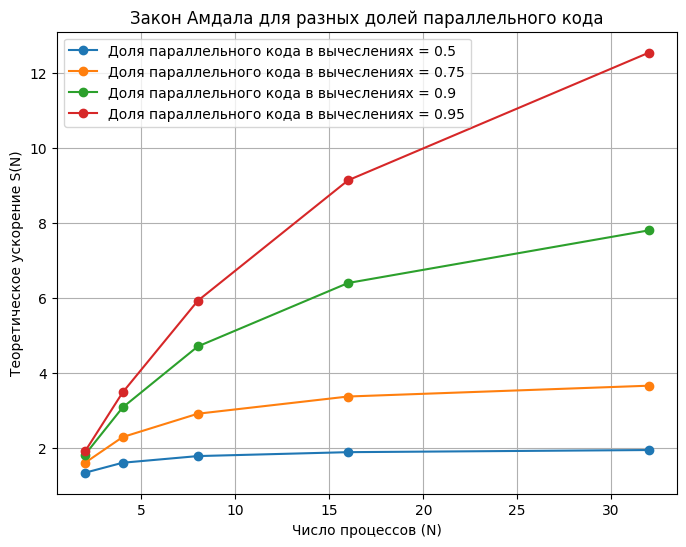
Подробные расчеты приведены ниже.

Для 50% параллельной работы (p = 0.5):

N = 2:
Speedup = (1 - 0.5) + (0.5 / 2) = 0.5 + 0.25 = 0.75 = 1.33

N = 4:
Speedup = (1 - 0.5) + (0.5 / 4) = 0.5 + 0.125 = 0.625 = 1.60

N = 8:
Speedup = (1 - 0.5) + (0.5 / 8) = 0.5 + 0.0625 = 0.5625 = 1.77

N = 16:
Speedup = (1 - 0.5) + (0.5 / 16) = 0.5 + 0.03125 = 0.53125 = 1.88

N = 32:
Speedup = (1 - 0.5) + (0.5 / 32) = 0.5 + 0.015625 = 0.515625 = 1.94

Для 75% параллельной работы (p = 0.75):

N = 2:
Speedup = (1 - 0.75) + (0.75 / 2) = 0.25 + 0.375 = 0.625 = 1.60

N = 4:
Speedup = (1 - 0.75) + (0.75 / 4) = 0.25 + 0.1875 = 0.4375 = 2.29

N = 8:
Speedup = (1 - 0.75) + (0.75 / 8) = 0.25 + 0.09375 = 0.34375 = 2.91

N = 16:
Speedup = (1 - 0.75) + (0.75 / 16) = 0.25 + 0.046875 = 0.296875 = 3.37

N = 32:
Speedup = (1 - 0.75) + (0.75 / 32) = 0.25 + 0.0234375 = 0.2734375 = 3.66

Для 90% параллельной работы (p = 0.9):

N = 2:
Speedup = (1 - 0.9) + (0.9 / 2) = 0.1 + 0.45 = 0.55 = 1.82

N = 4:
Speedup = (1 - 0.9) + (0.9 / 4) = 0.1 + 0.225 = 0.325 = 3.08

N = 8:
Speedup = (1 - 0.9) + (0.9 / 8) = 0.1 + 0.1125 = 0.2125 = 4.71

N = 16:
Speedup = (1 - 0.9) + (0.9 / 16) = 0.1 + 0.05625 = 0.15625 = 6.40

N = 32:
Speedup = (1 - 0.9) + (0.9 / 32) = 0.1 + 0.028125 = 0.128125 = 7.81

Для 95% параллельной работы (p = 0.95):

N = 2:
Speedup = (1 - 0.95) + (0.95 / 2) = 0.05 + 0.475 = 0.525 = 1.90

N = 4:
Speedup = (1 - 0.95) + (0.95 / 4) = 0.05 + 0.2375 = 0.2875 = 3.47

N = 8:
Speedup = (1 - 0.95) + (0.95 / 8) = 0.05 + 0.11875 = 0.16875 = 5.93

N = 16:
Speedup = (1 - 0.95) + (0.95 / 16) = 0.05 + 0.059375 = 0.109375 = 9.14

N = 32:
Speedup = (1 - 0.95) + (0.95 / 32) = 0.05 + 0.0296875 = 0.0796875 = 12.54

Работа с кодом

Теперь произведем вычисления нашей функции. Допустим, мы не знаем, какой % времени наша функция работает параллельно и можем вычислить только коэффициент ускорния.
Запустим код и нанесем на график полученные значения

import multiprocessing
import time
import random
import matplotlib.pyplot as plt

def partial_sum(arr):
    return sum(arr)

def parallel_sum(arr, num_processes):
    chunk_size = len(arr) // num_processes
    chunks = [arr[i * chunk_size : (i + 1) * chunk_size] for i in range(num_processes)]

    with multiprocessing.Pool(num_processes) as pool:
        results = pool.map(partial_sum, chunks)

    return sum(results)

if __name__ == "__main__":
    N_values = [1, 2, 4, 8, 16, 32]
    array = [random.randint(1, 100) for _ in range(10**7)]  # Увеличенный массив

    serial_time = time.time()
    result = parallel_sum(array, 1)  # Время для одного процесса (серийный случай)
    serial_time = time.time() - serial_time

    speedups = []

    for N in N_values:
        start_time = time.time()
        result = parallel_sum(array, N)
        elapsed_time = time.time() - start_time
        speedup = serial_time / elapsed_time  # Рассчитываем ускорение
        speedups.append(speedup)
        print(f"N = {N}, Sum = {result}, Time = {elapsed_time:.5f} sec, Speedup = {speedup:.2f}")

    # Построение графика
    plt.plot(N_values, speedups, marker='o')
    plt.xlabel("Число процессов (N)")
    plt.ylabel("Ускорение (Speedup)")
    plt.title("Ускорение параллельной суммы в зависимости от числа процессов")
    plt.grid(True)
    plt.show()

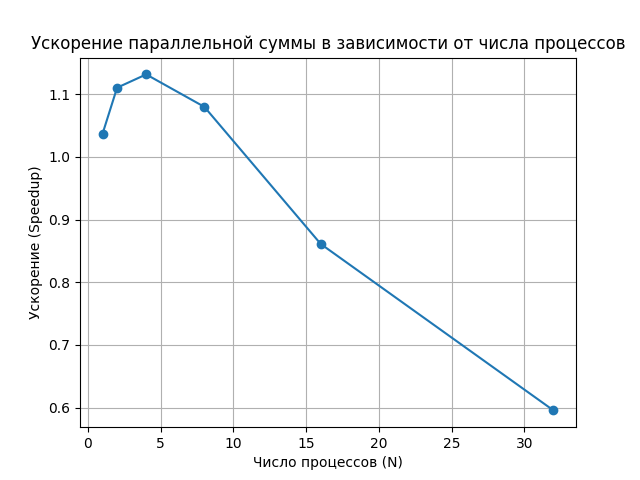
Проанализируем поведения функции. Как видим своё максимально значение измерения достигают при N=4.
Приэтом дальше коэффициент ускорения падает. Почему так происходит?
Проблема связана с накладными расходами. Они возникают вследствие потребности обсулживать потоки.
Нам же выгодно создавать потоки до тех пор, пока наблюдается прирост производительности.

По характеру прироста вы можете определить p - долю участков кода, выполняющегося парралельно.

N = 1, Sum = 504867736, Time = 0.51550 sec, Speedup = 1.04
N = 2, Sum = 504867736, Time = 0.48137 sec, Speedup = 1.11
N = 4, Sum = 504867736, Time = 0.47235 sec, Speedup = 1.13
N = 8, Sum = 504867736, Time = 0.49501 sec, Speedup = 1.08
N = 16, Sum = 504867736, Time = 0.62073 sec, Speedup = 0.86
N = 32, Sum = 504867736, Time = 0.89745 sec, Speedup = 0.60

Tip

Если внимательно изучить теоретический график, то можно легко определить, что наша паррелизация на уровне около p = 0.5. Почему так? Посколько наибольший участок прироста с 1 до 4, остальные процессы начинают идти в убыль.

Список источников

1. Сравнение производительности GPU-расчетов на Python и C
2. Python в три ручья: работаем с потоками (часть 1)