Арифметические основы вычислений#

Основными ячейками компьютерной памяти являются бит и байт.
Бит (bit, binary digit – двоичная цифра) – это минимальная ячейка памяти, которая может хранить один двоичный разряд (значения «0» или «1»).

Последовательность смежных двоичных цифр длиной в 8 бит получила название байт (byte, binary term).
Байт – это наименьшая адресуемая компьютером единица информации.

Максимально возможное число, которое размещается в байте, в двоичном формате будет состоять из восьми единиц, а в шестнадцатеричном – из двух цифр FF:

1111 1111₂ = FF₁₆ = 255₁₀.

Слово (word) – это совокупность нескольких байт, которую процессор обрабатывает как единое целое. Процессор производит операции именно над словами, например, считывает из памяти слово целиком и записывает в память, складывает или умножает два слова и т. д.

Размер слова зависит от разрядности процессора, которая, в свою очередь, определяется разрядностью основных регистров процессора. Например:

У 16-разрядного процессора Intel 8086 основные регистры были 16-разрядные, и размер слова был равен двум байтам.
У 32-разрядного процессора Intel Core основные регистры имеют разрядность 32 бита, поэтому размер слова у него – четыре байта.

Максимально возможное целое число, которое можно поместить в двухбайтовое слово:

1111 1111 1111 1111_2 = FFFF_16 = 65 535_10.

Для 32-разрядного слова максимальное число будет следующим:

1111 1111 1111 1111 1111 1111 1111 1111₂ = FFFF FFFF₁₆ = 4 294 967 295₁₀.

Большинство современных процессоров 32- или 64-разрядные.

Следует отметить, что разрядность ячеек памяти, начиная с байта, увеличивается каждый раз вдвое, то есть используются ячейки размером:

1 байт
2 байта
4 байта
8 байт
16 байт

Но не применяются ячейки размером 7 или 9 байтов.

Представление целых чисел в памяти компьютера#

Машинное представление чисел неразрывно связано с понятием типа данных.

Определение

**Тип данных** – это характеристика данных, определяющая:
- диапазон их значений,
- набор допустимых операций над ними,
- внутреннее представление в памяти компьютера.

Типы данных для хранения целых чисел делятся на беззнаковые и знаковые.

Беззнаковые типы данных могут хранить только неотрицательные целые числа.
Знаковые предназначены для хранения и положительных, и отрицательных чисел.

Рассмотрим сначала беззнаковые типы.

Представление беззнаковых чисел в памяти#

Числа беззнаковых типов хранятся в памяти в двоичном виде.
Для получения представления беззнакового десятичного числа в памяти компьютера:
1. Переводим число в двоичную систему счисления.
2. Дописываем незначащие нули слева до нужной разрядности.

Задача:
Пусть имеется десятичное целое число 100.
В каком типе данных его можно представить?
Сколько требуется бит для хранения числа?
Каково будет его внутреннее (машинное) представление?

Решение:
1. Переведем число в двоичную систему:
$100_{10} = 110\ 0100_2 = 64_{16}.$
2. По количеству бит (7) видно, что для хранения такого числа понадобится минимум 8-разрядная ячейка памяти.
В Паскале это беззнаковый тип Byte.

Внутреннее представление числа в памяти (дополним слева незначащим нулем до разрядности 8 бит):
$100_{10} = 0110\ 0100_2 = 64_{16}.$
Это число можно разместить и в 16-битном беззнаковом типе
(например, Word), дополнив уже 9 незначащими нулями:
$100_{10} = 0000\ 0000\ 0110\ 0100_2 = 0064_{16}.$

Представление знаковых чисел в памяти#

Для представления знаковых целых чисел используются три способа:
1. Прямой код;
2. Обратный код;
3. Дополнительный код.

Все три способа используют самый левый (старший) разряд битового набора
длины $k$ для кодирования знака числа:
- знак "плюс" кодируется нулем ( $0$ ),
- знак "минус" — единицей ( $1$ ).

Остальные $k-1$ разрядов (называемые мантиссой или цифровой частью)
используются для представления абсолютной величины числа.

Прямой код#

При записи числа в прямом коде (англ. Signed magnitude representation) старший разряд является знаковым разрядом. Если его значение равно нулю, то представлено положительное число или положительный ноль. Если старший разряд равен единице, то представлено отрицательное число или отрицательный ноль. В остальных разрядах (которые называются цифровыми) записывается двоичное представление модуля числа.

Пример:
Число −5 в восьмибитном типе данных, использующем прямой код, будет выглядеть так: 10000101.

Диапазон чисел в n-битовом типе данных:
В n-битовом типе данных можно представить диапазон чисел:

$[-2^{n-1}+1; 2^{n-1}-1]$

Достоинства представления чисел с помощью прямого кода:
1. Получить прямой код числа достаточно просто.
2. Из-за того, что 0 обозначает +, коды положительных чисел относительно беззнакового кодирования остаются неизменными.
3. Количество положительных чисел равно количеству отрицательных.

Недостатки представления чисел с помощью прямого кода:
1. Выполнение арифметических операций с отрицательными числами требует усложнения архитектуры центрального процессора. Например, для вычитания невозможно использовать сумматор, необходима отдельная схема для этого.
2. Существуют два нуля: −0 (100…000) и +0 (000…000), что усложняет арифметическое сравнение.
3. Из-за весьма существенных недостатков прямой код используется очень редко.

Обратный код#

Обратный код двоичного числа образуется по следующему правилу:
- Обратный код положительных чисел совпадает с их прямым кодом.
- Обратный код отрицательного числа содержит единицу в знаковом разряде числа, а значащие разряды числа заменяются на инверсные, т.е. нули заменяются единицами, а единицы — нулями.

Пример:
1. $A_{10} = +10$ , $A_2 = +1010$ , $[A_2]_{\text{ок}} = [A_2]_{\text{п}} = 0|1010$
2. $V_{10} = -15$ , $V_2 = -1111$ , $[V_2]_{\text{ок}} = 1|0000$

Свое название обратный код получил, потому что коды цифр отрицательного числа заменены на инверсные.

Важные свойства обратного кода:
1. Сложение положительного числа $C$ с его отрицательным значением в обратном коде дает т.н. машинную единицу $M_{E\text{ок}} = 1|11…11$ , состоящую из единиц в знаковом и в значащих разрядах числа.
2. Нуль в обратном коде имеет двоякое значение. Он может быть как положительным числом $0|00…00$ , так и отрицательным $1|11…11$ . Значение отрицательного числа совпадает с машинной единицей $M_{E\text{ок}}$ .
3. Двойственное представление нуля явилось причиной того, что в современных ЭВМ все числа представляются не обратным, а дополнительным кодом.

Код с дополнением до единицы (Ones' Complement)#

Код с дополнением до единицы является альтернативным способом представления целых чисел. Алгоритм получения кода числа следующий:

Если число положительное, то в старший разряд (который является знаковым) записывается ноль, а далее записывается само число.
Если число отрицательное, то код получается инвертированием представления модуля числа (получается обратный код).
Если число является нулем, то его можно представить двумя способами:
$+0$ (000…000)
$-0$ (111…111)

Пример:
Переведём число −13 в двоичный восьмибитный код.
- Прямой код модуля числа $13$ : 00001101.
- Инвертируем его и получаем: 11110010.

Для получения из дополнительного кода самого числа достаточно инвертировать все разряды кода.

Диапазон значений:
Используя код с дополнением до единицы в n-битовом типе данных, можно получить диапазон значений:

$[-2^{n-1}+1; 2^{n-1}-1]$

Достоинства представления чисел с помощью кода с дополнением до единицы:
1. Простое получение кода отрицательных чисел.
2. Из-за того, что $0$ обозначает +, коды положительных чисел относительно беззнакового кодирования остаются неизменными.
3. Количество положительных чисел равно количеству отрицательных.

Недостатки представления чисел с помощью кода с дополнением до единицы:
1. Выполнение арифметических операций с отрицательными числами требует усложнения архитектуры центрального процессора.
2. Существуют два нуля: +0 и −0.

Однако в дополнительном коде представление нуля единственно, в отличие от прямого и обратного кодов, где ноль имеет два представления.

Дополнительный код (дополнение до двух) (Two's complement))#

Чаще всего для представления отрицательных чисел используется код с дополнением до двух (Two's Complement).

Алгоритм получения дополнительного кода числа:

Если число неотрицательное, то в старший разряд записывается ноль, далее записывается само число.
Если число отрицательное:
Все биты модуля числа инвертируются (все единицы меняются на нули, а нули — на единицы).
К инвертированному числу прибавляется единица.
К результату дописывается знаковый разряд, равный единице.

Пример:
Переведём число −5 в дополнительный восьмибитный код:
- Прямой код модуля −5: 00000101
- Обратный код: 1111010
- Прибавляем 1: 1111011
- Приписываем 1 как знаковый разряд: 11111011

Математическое представление:
Дополнительный код отрицательного числа A, хранящегося в n битах, равен:

$2^n - |A|$

По сути, дополнительный код представляет собой дополнение |A| до 0. Это связано с тем, что в n-разрядной арифметике $2^n = 0$ (в двоичной записи этого числа — единица и n нулей), и в n-разрядной ячейке помещаются только n младших разрядов.

Следовательно, верно равенство:

$2^n - |A| + |A| = 0$

Пример восстановления числа из дополнительного кода:
Переведём 11111011 обратно в число:
- Инвертируем: 00000100
- Прибавляем 1: 00000101
- Получаем модуль исходного числа −5.

Проверим:

$11111011 + 00000101 = 100000000$

Диапазон значений:
Дополнительный код представляет диапазон значений:

$[-2^{n-1}; 2^{n-1} - 1]$

Tip

Дополнительный код удобно использовать для вычислений в длинной арифметике, особенно для операций сложения и вычитания. Эти операции удобно выполнять с числами одинаковой длины.
Для этого в старшие разряды меньшего числа помещаются нули (если число положительное) или единицы (если число отрицательное).

Так числа будут выглядеть следующим образом:
- В старших разрядах бесконечное количество нулей (или единиц).
- В младших разрядах — сами данные числа.

Операцию сложения можно выполнить только один раз для старших битов, определяя знак получившегося числа. Вычитание выполняется просто: инвертируем число, прибавляем единицу, получаем число с минусом, затем делаем сложение.

Умножение с числами, представленными дополнительным кодом, не всегда оптимально: наивный алгоритм работает за O(n²), а более сложные алгоритмы — слишком трудоемкие. Лучше использовать прямой код для умножения, а для деления — тоже предпочтительнее прямой код.

Достоинства представления чисел с помощью кода с дополнением до двух:

Возможность заменить операцию вычитания операцией сложения, что упрощает архитектуру процессора и увеличивает быстродействие.
Нет проблемы двух нулей (однозначность представления нуля).

Недостатки представления чисел с помощью кода с дополнением до двух:

Ряд положительных и отрицательных чисел несимметричен, но это не так важно, поскольку дополнительный код решает гораздо более важные задачи для представления целых чисел.
Числа в дополнительном коде нельзя сравнивать как беззнаковые или вычитать без расширения разрядности.

Несмотря на некоторые недостатки, дополнение до двух в современных вычислительных системах используется чаще всего благодаря своей простоте и удобству для выполнения арифметических операций.

Тонкости битового представления целых чисел в Python#

Как известно, в Python целые числа ограничены лишь объёмом оперативной памяти, что позволяет им быть весьма большими. В этом контексте представление целых чисел может быть интерпретировано следующим образом: если число положительное, то его битовая запись начинается с бесконечного числа нулей. Если число отрицательное, то битовая запись начинается с бесконечного числа единиц.

Пример записи чисел:

Число 21: Оно будет записано как ...00010101, где слева — бесконечное количество нулей, а справа — двоичная запись числа $21$ .
Число -1: Это число записывается как бесконечная последовательность единиц: ...111.
Число 0: Записывается как бесконечная последовательность нулей: ...000.
Число ~21: Это будет последовательность ...11101010, то есть бесконечное количество единиц, за которыми следует побитовая инверсия числа 21.
Если число положительное (битовая запись начинается с нулей), то можно просто отбросить ведущие нули и интерпретировать число как обычное двоичное.
Если число отрицательное (битовая запись начинается с единиц), то нужно искать самую правую единицу, после которой идут только единицы. Эта единица разделяет число на две части:
"Голову", которая состоит из бесконечных единиц, и
"Хвост", который идет после первого нуля.

Пример:

Число ~21: Если число 21 записано как ...00010101, то побитовая инверсия $~21$ будет записана как ...11101010. Из этого числа мы видим, что оно состоит из бесконечного числа единиц и части 01010 (вторая часть после первого нуля). Это значение можно интерпретировать как разность двух чисел:

$...11101010 = 0b1010 - 0b100000 = -22$

В Python операция побитового отрицания (~) выполняется как инверсия всех битов числа, но важно помнить, что она работает по следующему правилу:

$\sim x = -1 - x$

Это означает, что если мы применяем операцию побитового отрицания к числу $x$ , результат будет равен $-1 - x$ .

Таким образом, в Python побитовое отрицание числа является способом получить его противоположное значение с учётом представления чисел в памяти как бесконечных последовательностей единиц или нулей в зависимости от знака числа.

Представление вещественных чисел#

Вещественные числа обычно представляются в виде чисел с плавающей запятой. Числа с плавающей запятой — один из возможных способов представления действительных чисел, который является компромиссом между точностью и диапазоном принимаемых значений, его можно считать аналогом экспоненциальной записи чисел, но только в памяти компьютера.

Число с плавающей запятой состоит из набора отдельных двоичных разрядов, условно разделенных на так называемые знак (англ. sign**), порядок (англ. *exponent) и мантиссу (англ. mantissa).

В наиболее распространённом формате (стандарт IEEE 754) число с плавающей запятой представляется в виде набора битов, часть из которых кодирует собой мантиссу числа, другая часть — показатель степени, и ещё один бит используется для указания знака числа (0 — если число положительное, 1 — если число отрицательное). При этом порядок записывается как целое число в коде со сдвигом, а мантисса — в нормализованном виде, своей дробной частью в двоичной системе счисления.

Представление числа в нормализованном экспоненциальном виде#

Возьмем, к примеру, десятичное число .
Представим это число в нормализованном экспоненциальном виде:
$1.55625 \times 10^2 = 1.55625 \times \exp{(10^2)}$
Число $1.55625 \times \exp{(10^2)}$ состоит из двух частей:
- Мантисса: $M = 1.55625$
- Экспонента: $\exp{10} = +2$

Если мантисса находится в диапазоне $1 \leq M < 10$ , то число считается нормализованным.
Экспонента представлена основанием системы исчисления (в данном случае 10) и порядком (в данном случае $+2$ ).

Порядок экспоненты может быть отрицательным, например, число $0.0155625 = 1.55625 \times \exp{(10^{-2})}$ .

Представление числа в денормализованном экспоненциальном виде#

Теперь рассмотрим представление числа в денормализованном экспоненциальном виде.
Возьмем то же число и представим его как:
$0.155625 \times 10^3 = 0.155625 \times \exp{(10^3)}$
Число $0.155625 \times \exp{(10^3)}$ состоит из двух частей:
- Мантисса: $M = 0.155625$
- Экспонента: $\exp{10} = +3$

Если мантисса находится в диапазоне $0.1 \leq M < 1$ , то число считается денормализованным.
Экспонента представлена основанием системы исчисления (в данном случае 10) и порядком (в данном случае $+3$ ).

Порядок экспоненты может быть отрицательным, например, число $0.0155625 = 0.155625 \times \exp{(10^{-3})}$ .

Преобразование десятичного числа в двоичное число с плавающей точкой#

Наша задача сводится к представлению десятичного числа с плавающей точкой в двоичное число с плавающей точкой в экспоненциальном нормализованном виде. Для этого разложим заданное число по двоичным разрядам:

$155.625 = 1 \times 2^7 + 0 \times 2^6 + 0 \times 2^5 + 1 \times 2^4 + 1 \times 2^3 + 0 \times 2^2 + 1 \times 2^1 + 1 \times 2^0 + 1 \times 2^{-1} + 0 \times 2^{-2} + 1 \times 2^{-3}$
$155.625 = 128 + 0 + 0 + 16 + 8 + 0 + 2 + 1 + 0.5 + 0 + 0.125$
$155.625_{10} = 10011011.101_2 \quad \text{— число в десятичной и в двоичной системе с плавающей точкой}$

Приведем полученное число к нормализованному виду в десятичной и двоичной системе:
$1.55625 \times \exp{(10^2)} = 1.0011011101 \times \exp{(2^{+111})}$

В результате мы получили основные составляющие экспоненциального нормализованного двоичного числа:
- Мантисса: $M = 1.0011011101$
- Экспонента: $\exp{2} = +111$

Стандарт IEEE 754#

Основное применение в технике и программировании получили форматы 32 и 64 бита.
Например, в VB используют типы данных single (32 бита) и double (64 бита).
В Cи аналогично используют float (32 бита) и double (64 бита).

Рассмотрим преобразование двоичного числа $10011011,101_2$ в формат single-precision (32 бита) стандарта IEEE 754.
Остальные форматы представления чисел в IEEE 754 являются увеличенной копией single-precision.

Чтобы представить число в формате IEEE 754 (single-precision), его необходимо привести к нормализованному двоичному виду.
Ранее мы проделали это преобразование над числом $155.625_{10}$ . Теперь рассмотрим, как оно представляется в 32-битном формате IEEE 754.

Число может быть положительным или отрицательным, поэтому 1 бит отводится для знака:
$0$ — положительное
$1$ — отрицательное
Этот бит — старший в 32-битной последовательности.
Экспонента кодируется 8 битами.
Она может быть положительной или отрицательной, но для удобства к ней добавляют смещение ( $+127$ ), чтобы избежать дополнительного бита знака:
Если (), то смещённая экспонента:
$E' = 7 + 127 = 134_{10} = 10000110_2$
Если , то
$E' = 127 - 7 = 120_{10} = 01111000_2$
Чтобы получить реальную экспоненту числа, из записанного значения нужно вычесть 127.
Мантисса записывается в оставшиеся 23 бита.
Так как у нормализованного двоичного числа первый бит всегда 1 ( $1 \leq M < 2$ ), его не записывают в 23-битное поле.
В эти 23 бита записывают остаток мантиссы.

Пример: представление числа 155.625 в IEEE 754 (32 бита)#

Рассчитаем IEEE 754-представление для $155.625_{10}$ .

Переведём число в двоичную систему:
$155.625_{10} = 10011011.101_2$
Приведём к нормализованному виду:
$1.0011011101_2 \times 2^7$
Здесь:
Мантисса: $1.0011011101_2$
Экспонента: $7_{10}$
Смещённая экспонента:
$7 + 127 = 134_{10} = 10000110_2$
Мантисса (без первой единицы):
$00110111010000000000000_2$
Итоговое представление:

Знак (1 бит)	Экспонента (8 бит)	Мантисса (23 бита)	IEEE 754 (HEX)
0	10000110	00110111010000000000000	431BA000

В результате десятичное число 155.625 представлено в IEEE 754 (single-precision) как:
$\mathbf{431BA000_{16}}$

Преобразования числа формата 32 бит IEEE 754 в десятичное число#

Чтобы записать число в стандарте IEEE 754 или восстановить его, необходимо знать три параметра:
- S — бит знака (31-й бит)
- E — смещенная экспонента (30-23 биты)
- M — остаток от мантиссы (22-0 биты)

Эти целые числа записаны в числе IEEE 754 в двоичном виде.

Формула для 32 нормализованных бит IEEE 754, где $F$ — десятичное число:

$F = (-1)^S \cdot 2^{(E - 127)} \cdot \left( 1 + \frac{M}{2^{23}} \right)$

Здесь:
- $(-1)^S$ — знак числа
- $2^{(E - 127)}$ — экспонента с учетом смещения 127
- $1 + \frac{M}{2^{23}}$ — мантисса, где 1 — это единица, которую мы выбросили из 23 бит мантиссы, а $\frac{M}{2^{23}}$ — остаток мантиссы в десятичном виде.

Проверим наш пример, где:
- $S = 0$ (число положительное),
- $E = 134$ ,
- $M = 1810432$ .

По формуле получаем:

$F = (-1)^0 \cdot 2^{(134 - 127)} \cdot \left( 1 + \frac{1810432}{2^{23}} \right)$
$F = 1 \cdot 2^7 \cdot \left( 1 + \frac{1810432}{8388608} \right)$
$F = 128 \cdot \left( 1 + 0.2158203125 \right) = 128 \cdot 1.2158203125 = 155.625$

Как видим, результат совпадает с исходным числом 155,625.

Не все десятичные числа имеют двоичное представление с плавающей запятой

Пример: «0,2» - «0,200000003» в одинарной точности

Формальное представление чисел в стандарте IEEE 754 для любого формата точности.#

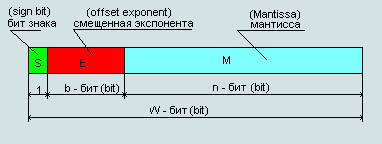
Формат чисел IEEE 754, где:

S — бит знака. Если $S = 0$ , то число положительное; если $S = 1$ , то число отрицательное.
E — смещенная экспонента двоичного числа.
$\text{exp}_2 = E - (2^{(b-1)} - 1)$ — экспонента двоичного нормализованного числа с плавающей точкой, где $(2^{(b-1)} - 1)$ — это смещение экспоненты (в 32-битном IEEE 754 оно равно +127).
M — остаток мантиссы двоичного нормализованного числа с плавающей точкой.

Формула нормализованных чисел IEEE 754 (Формула №1):

$(-1)^S \times 2^{\text{exp}_2} \times (1 + M)$

Используя формулу №1, вычислим формулы для нахождения десятичных чисел из форматов одинарной (32 бита) и двойной (64 бита) точности IEEE 754.

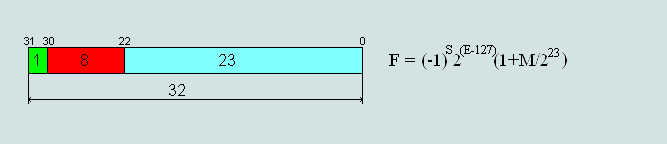
Формат числа одинарной точности (single-precision) — 32 бита

Формат 32 бита нормализованных чисел IEEE 754.

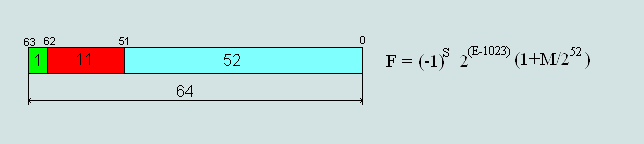
Формат числа двойной точности (double-precision) — 64 бита

Интерактивный калькулятор#

Проблемы компьютерных вычислений, вызванные использованием стандарта IEEE754.#

Стандарт IEEE 754 широко применяется в технике и программировании.
Большинство современных микропроцессоров изготовляются с аппаратной реализацией представления вещественных переменных в формате IEEE 754.

Язык программирования и программист не могут изменить эту ситуацию, иного представления вещественного числа в микропроцессоре не существует.

Когда создавали стандарт IEEE 754-1985, представление вещественной переменной в виде 4 или 8 байт казалось очень большой величиной, так как объём оперативной памяти MS-DOS был равен 1 Мб.
А программа в этой системе могла использовать только 0,64 Мб.

Для современных ОС размер в 8 байт является ничтожным, тем не менее переменные в большинстве микропроцессоров продолжают представлять в формате IEEE 754-1985.

Ошибки связанные с точностью представления вещественных чисел в формате IEEE754#

Данная ошибка всегда присутствую в компьютерных вычислениях.

      #include <iostream>

      int main() {
         float a, b, f;
         a = 123456789;
         b = 123456788;
         f = a - b;
         std::cout << "Result: " << f << std::endl;
         return 0;
      }

В коде используется тип float, который хранит числа с плавающей запятой в 32 бита (4 байта) и имеет ограниченную точность (~7 значащих десятичных цифр).

float не может точно представить 123456789, вместо этого число округляется.
В результате a ≈ 123456792, а b ≈ 123456784.

Если a ≈ 123456792, а b ≈ 123456784, то разница будет 8, а не 1.

Ошибки вызванные сдвигом мантисс. Циклические дыры.#

Хотя с относительной погрешностью здесь всё в порядке, есть и другие проблемы.
Во-первых, работать с числами можно только в узком диапазоне числовой оси, где мантиссы пересекаются.
Во-вторых, для каждого исходного числа существует предел выполнения цикла, называемый "Циклической дырой".

Рассмотрим пример задачии. В автоматической системе управления процессом фасовки таблетки из бункера, требуется вычислить изменение веса бункера после вычитания веса одной таблетки несколько миллионов раз.

Условия задачи:
- В начальный момент вес бункера равен 300 кг.
- Вес одной таблетки составляет 0.00001 кг.
- Таблетки забираются фасовочной машиной поочередно, процесс повторяется 10 миллионов раз.
- Изменение веса бункера вычисляется с использованием типа данных float, который имеет ограниченную точность.

#include <iostream>

int main() {
    float a = 0.00001f;  // вес таблетки в кг
    float c = 300.0f;    // исходный вес бункера в кг
    long n;              // количество циклов

    for (n = 1; n <= 10000000; n++) {
        c = c - a;  // одна таблетка забирается фасовочной машиной
    }

    std::cout << "Измененный вес бункера: " << c << " кг" << std::endl;

    return 0;
}

Tip

Если существует цикл, в котором исходное число суммируется с суммой, то существует численный предел суммы для этого числа.
То есть, сумма, достигнув определённой величины, перестаёт увеличиваться при её сложении с исходным числом.

Ошибки вызванные округлением. Грязный ноль.#

"Грязный ноль" — это ситуация, когда вы или программа считаете, что переменная, не равная нулю, равна нулю.

При компьютерных вычислениях можно выделить два вида округления:

Результат выполненной арифметической операции всегда округляется.
Вывод и ввод вещественного числа в окно Windows происходит с округлением.

В первом случае переменная округляется по одному из четырёх типов округления IEEE754. По умолчанию округление происходит к ближайшему целому.
При этом переменная принимает новое округлённое значение.

Во втором случае переменная не меняет своего значения, а просто в окно Windows выводится округлённое значение вещественного числа.
Получается, что исходная переменная и её отображение в окне Windows — это разные числа. Это не ошибка формата IEEE754, а ошибка Windows.

// Функция для замены запятой на точку
std::string replaceCommaWithDot(const std::string& input) {
    std::string output = input;
    for (size_t i = 0; i < output.length(); ++i) {
        if (output[i] == ',') {
            output[i] = '.';
        }
    }
    return output;
}

int main() {
    SetConsoleCP(1251);// установка кодовой страницы win-cp 1251 в поток ввода
    SetConsoleOutputCP(1251); // установка кодовой страницы win-cp 1251 в поток вывода
    double b, c;

    // Инициализация значения переменной a
    std::cout << "Инциализация a в коде " << std::setprecision(15) << a << std::endl;

    // Ввод числа с консоли
    std::string input;
    std::cout << "Введение вручную тоже самое число: ";
    std::getline(std::cin, input);

    // Замена запятой на точку
    input = replaceCommaWithDot(input);

    // Преобразование строки в число
    b = std::stod(input);

    // Вычисление разницы
    c = a - b;

    // Вывод результата
    std::cout << "Result: " << c << std::endl;

    return 0;
}

Дополнительные сведения: Перевод правильной дроби#

Пусть дано число $X_0$ , которое лежит в интервале $0 < X_0 < 1$ . Требуется перевести его в $P$ -ичную систему счисления, т.е. найти $X_P = 0.p_1 p_2 p_3 \dots p_t \dots$ , где $p_i$ принадлежат базису $\{0, 1, \dots, P-1\}$ , а $i$ принимает значения $-1, -2, -3, \dots$ .

Перевод дроби из $Q$ -ичной системы счисления в $P$ -ичную сводится к следующим правилам:

Умножить данное число на $P$ (основание новой системы счисления). Цифра, получившаяся в целой части произведения, является первой цифрой после запятой в искомом числе.
Дробную часть произведения умножить на $P$ . Цифра, получившаяся в целой части произведения, является следующей цифрой в искомом числе.
Если дробная часть произведения равна нулю или достигнута заданная точность представления числа в новой системе счисления, то результат получен. Иначе повторить п. 2.

Пример

Дано число $0.225_{10}$ . Переведем его в восьмеричную систему счисления, сохраняя в результате четыре цифры после запятой:

$0.225 \times 8 = 1.800$
Цифра $1$ — это первая цифра после запятой.

$0.800 \times 8 = 6.400$
Цифра $6$ — это вторая цифра после запятой.

$0.400 \times 8 = 3.200$
Цифра $3$ — это третья цифра после запятой.

$0.200 \times 8 = 1.600$
Цифра $1$ — это четвертая цифра после запятой.

$0.600 \times 8 = 4.800$
Так как мы уже достигли четырех цифр, результат получен.

Итак, $0.225_{10} = 0.1631_8$ .

Примечание: Как показано в последнем примере, перевод дробей может представлять собой бесконечный процесс, особенно если дробь не имеет конечного представления в новой системе счисления. Это приводит к тому, что результат перевода всегда является приближённым. Количество цифр в числе, представленном в системе счисления с основанием $p$ , определяется точностью, с которой необходимо представить число в системе счисления с основанием $q$

Соблюдая авторские права#

При подготовке матрериала были использованы (великолепные конспекты)[http://softelectro.ru/ieee754.html], хотя примеры и были мной переписаны на с++ и проверена их актуальность.