Введение в асимптотический анализ. Рекурсивные функции.

Презентация

Исследование рекурсии занимает отдельную область в информатике, называемую теорией рекурсии. Поскольку невозможно охватить всю эту область, мы рассмотрим лишь ключевые особенности, которые стали основой для многих программистов.

Note

Рекурсивная функция (recursive function) – функция, в теле которой присутствует вызов самой себя

Концепция самоссылочных сущностей, способных воспроизводить себя, глубоко укоренилась в информатике. Рассмотрим простые примеры и увидим элегантность рекурсии.

Возьмём, например, функцию факториала:

$$n! = n_k \times ... \times n_1 \times n_0, \quad k \in \mathbb{N}$$

Другой способ выразить эту функцию:

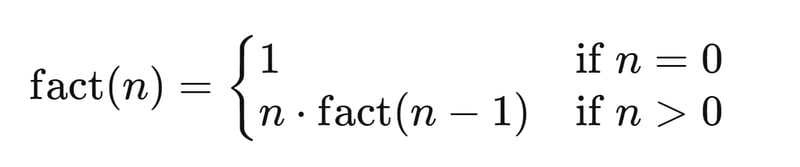
Вычисление факториала принимает число и связывает его с вычислением факториала для числа, уменьшенного на 1. Рассмотрим следующий псевдокод:

function factorial(int:a):
    if a == 0 return 1
    return a * factorial(a-1)

Давайте заместим рекурсивную функцию, используя цикл while - такой подход называется итеративным

function factorial(int: a):
    int result = 1
    while a > 1: 
        result *= a
        a -= 1

Рекурсивный вызов функции состоит из двух основных частей:

1. Базовый случай — условие, при котором рекурсия останавливается.
2. Индуктивный случай — правила, которые уменьшают задачу до базового случая.

Продолжим вводить определения. В целом, существуют два типа рекурсии: прямая и косвенная.

Прямая рекурсия — это когда функция вызывает саму себя напрямую. Код, который мы рассмотрели ранее, является примером прямой рекурсии.
Косвенная рекурсия происходит, когда одна функция вызывает другую, а та, в свою очередь, снова вызывает первую. Например:

    function print(int: a):
        print a + " × "
        return a * factorial(a-1)

    function factorial(int: a):
        if a == 0 return 1
        print(a)

Косвенную рекурсию можно расширить, если цепочка вызовов функций образует цикл:
g₁(x₁) → g₂(x₂) → ... → g₁(xₙ)

Здесь функция g₁ вызывает g₂, затем g₂ вызывает следующую функцию, и так далее, пока одна из функций снова не вызовет g₁. Это приводит к зацикливанию, если нет условия завершения.

Вычиление рекурсивной функции

Рекурсивная функция работает в два этапа:

• Прямой ход рекурсии (углубление) – функция вызывает саму себя, пока не достигнет условия выхода.
• Обратный ход рекурсии (возвращение) – начинается, когда выполнено условие выхода, и вычисления сворачиваются, возвращаясь по цепочке вызовов.

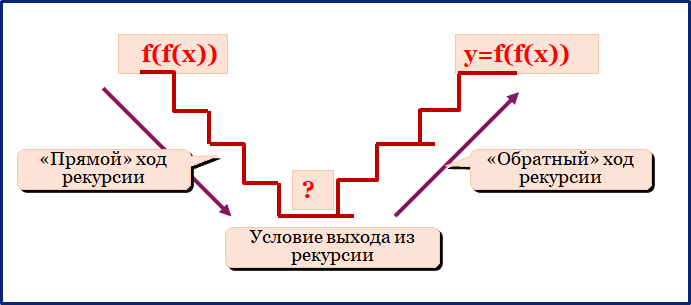
Прямой ход рекурсии
- Функция вызывает саму себя с новыми аргументами, уменьшая задачу до более простых случаев.
- Новые вызовы функции откладываются в стеке вызовов.
- Глубина рекурсии увеличивается, пока не будет достигнуто условие выхода.
Обратный ход рекурсии
- Когда достигается условие выхода, функция начинает возвращать значения.
- Значения подставляются в предыдущие вызовы, вычисления выполняются по цепочке назад.
- Постепенно все отложенные вызовы завершаются, и программа возвращается к исходному вызову.
Условие выхода из рекурсии
- Это критическая часть рекурсивной функции, предотвращающая бесконечный вызов.
- Обычно выражается в виде if (условие) return значение;.
- Позволяет завершить рекурсию и начать обратный ход.

Вернемя к нашему псевдокоду и рассмотрим вызов функции factorial(5)

    function factorial(int:a):
        if a == 0 return 1
        return a * factorial(a-1)

1. factorial(5) вызывает factorial(4), factorial(4) вызывает factorial(3), и так далее… (прямой ход).
2. Когда factorial(0) возвращает 1, начинается обратный ход:
   factorial(1) = 1 * 1 = 1

factorial(2) = 2 * 1 = 2

factorial(3) = 3 * 2 = 6

factorial(4) = 4 * 6 = 24

factorial(5) = 5 * 24 = 120

Если представлять себе это в виде анимации, то вышла бы следующая картина:

Чтобы хранить порядок операций, необходимых для выполнения компьютер формируется стек вызова.

Стек вызовов функций (call stack)

Системный стек — это область памяти, используемая для хранения:
- Адресов возврата (куда возвращаться после выполнения функции).
- Локальных переменных функции.
- Аргументов, переданных в функцию.

Когда вызывается функция, для неё выделяется кадр стека (stack frame).
При выходе из функции её кадр удаляется, и управление передаётся по адресу возврата.

Warning

Рекурсивные функции могут занимать значительную часть стековой памяти для хранения адресов возврата!

Прямой ход рекурсии (вложенные вызовы)

Вызов	Аргумент n	Адрес возврата
factorial(3)	3	main()
factorial(2)	2	factorial(3)
factorial(1)	1	factorial(2)
factorial(0)	0	factorial(1) (условие выхода)

При выходе из функции из головы стека извлекается адрес возврата

Обратный ход рекурсии (разворачивание стека)

1. factorial(0) возвращает 1, удаляется из стека.
2. factorial(1) вычисляет 1 * 1, удаляется.
3. factorial(2) вычисляет 2 * 1, удаляется.
4. factorial(3) вычисляет 3 * 2, удаляется.

Любопытные заметки

Стек в операционной системе имеет ограниченный размер, который влияет на глубину рекурсии. Например, команда в Linux-системах:

ulimit -s 8192

устанавливает максимальный размер стека на 8192 килобайта.
Если программа использует слишком много памяти в стеке, например, из-за слишком глубокой рекурсии, может произойти переполнение стека (stack overflow).
Это может привести к сбоям в работе программы или системы.

Виды рекурсии

Линейная рекурсия (linear recursion) — это тип рекурсии, при котором в функции присутствует единственный рекурсивный вызов самой себя. Такой тип рекурсии обычно используется в задачах, где необходимо выполнить серию шагов, один за другим, например, в вычислении факториала.

Очевидно, что наш фрактал является линейной рекурсией, поскольку одна функция один раз вызывает саму себя

Однако легко представить себе и иной случай, когда функция в return вызывает себя два или более раз. Назовем такую структуру древовидной.

Древовидная рекурсия (или нелинейная рекурсия, non-linear recursion) — это тип рекурсии, при котором функция вызывает себя несколько раз. Это создает структуру данных, похожую на дерево, где каждый узел может иметь несколько дочерних вызовов. Такой тип рекурсии часто используется в сложных задачах, таких как обход деревьев или решение задач с множеством вариантов.

Осталось только придумать подходящий алгоритм для иллюстрации.

Числа Фибоначчи

Тысячу лет назад люди увлекались вовсе не нейросетями, а числами и их свойствами. Так, в XII веке главным трендом были загадочные числа Фибоначчи, следы которых и сейчас можно найти практически везде: от расположения лепестков на дереве до формы ураганов и галактик.

Числа Фибоначчи — это последовательность чисел, которые задаются по определённому правилу. Оно звучит так: каждое следующее число равно сумме двух предыдущих.
Первые два числа заданы сразу и равны 0 и 1.

Вот как выглядит последовательность Фибоначчи:

    0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, … , ∞

Длиться этот числовой ряд может бесконечно, но для большинства задач обычно хватает первых десяти чисел:

первое — 0;
второе — 1;
третье — 1;
четвёртое — 2;
пятое — 3;
шестое — 5;
седьмое — 8;
восьмое — 13;
девятое — 21;
десятое — 34.

Ну умеем мы складывать числа друг с другом, и что с того? Можно придумать ещё несколько таких же последовательностей — например, где следующее число будет равно сумме трёх или четёрых предыдущих. Как это пригодится в науке и технике? Но обо всём по порядку.

Как появились числа Фибоначчи

Первым эту последовательность описал итальянский учёный Леонардо Пизанский по прозвищу Фибоначчи. Он жил в XII веке и усердно изучал работы античных и индийских математиков. В них Леонардо нашёл много полезных знаний — например, что десятичная система удобнее, чем римская нотация, и что по ней проще считать.

Полученные знания Леонардо систематизировал в своём главном труде — «Книге абака». Там же появилось и первое упоминание о числах Фибоначчи — как ни странно, в контексте решения задачи о кроликах:

Задача о размножении кроликов

Постановка задачи

В огороженный загон посадили двух кроликов — самку и самца. 
Каждый месяц пара являет миру ещё одну пару кроликов.
Вопрос: сколько пар кроликов будет в загоне через год?

Конечно, решить эту задачу не так просто, потому что на размножение кроликов влияет много факторов — например, они могут умереть или убежать. Поэтому Леонардо ограничил задачу такими условиями:

• кролики не могут умереть;
• они достигают половой зрелости за месяц;
• самки беременны ровно месяц;
• кролики всегда рождаются парами: самка + самец.

Теперь задачу вполне можно решить: ответом на неё как раз будет последовательность Фибоначчи. Логика такая: каждая взрослая пара кроликов будет создавать ещё одну пару через месяц после рождения. Эти кролики-дети будут расти месяц, а потом размножаться с другими кроликами. И так двенадцать месяцев.

Чуть лучше этот процесс можно представить с помощью этой схемы:

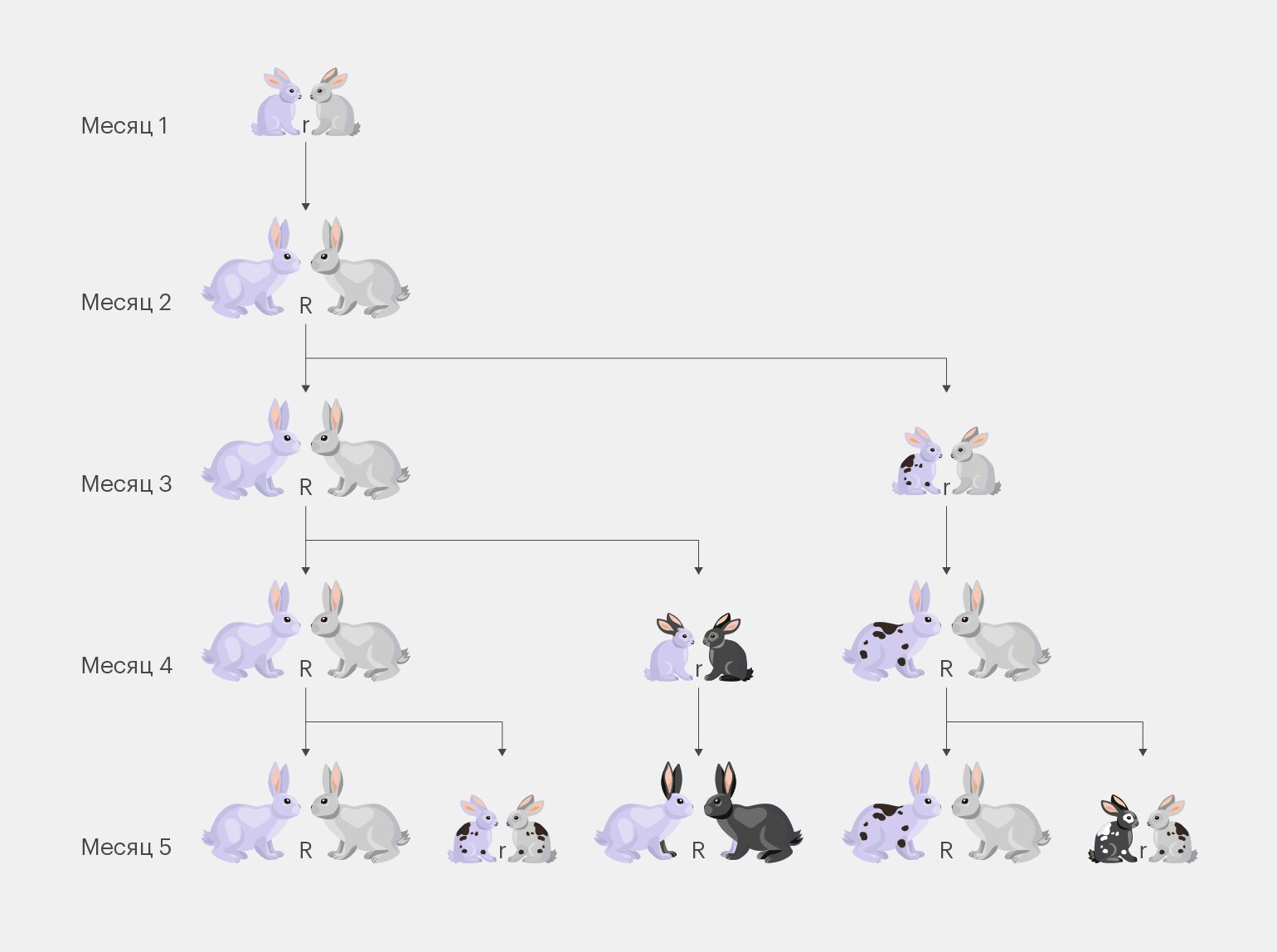
Смотрите, первая пара кроликов ещё совсем молодая, поэтому пока не может дать потомство. Но уже через месяц кролики подрастут и смогут размножаться — соответственно, на третий месяц пар будет уже две. Дальше количество пар будет равняться сумме пар за два предыдущих месяца, и последовательность примет уже знакомый нам вид:

Получаем ответ на задачу: 233 пары кроликов.

И в этом весь смысл чисел Фибоначчи — считать кроликов в загоне? Нет! Оказывается, Леонардо лишь приоткрыл дверь в возможности этой последовательности. Основное применение она нашла в математике, архитектуре и искусстве.

Архитекторы античных и средневековых городов много времени уделяли идеальным пропорциям. Они хотели создавать красивые постройки, которыми бы наслаждались все жители города. Так появилось понятие золотого сечения.

Золотое сечение — это число, которое помогает делить вещи на красивые части. Оно равно примерно 1,618. Золотое сечение можно найти так: если взять два отрезка чего-то, то большой отрезок должен быть в 1,618 раза больше маленького отрезка, а вся вещь должна быть в 1,618 раза больше большого отрезка. Это число называется «фи» и пишется так: φ.

Вернёмся к числам Фибоначчи. Оказывается, отношение каждого числа к предыдущему примерно равно значению золотого сечения. Правда, на первых числах последовательности этого не будет заметно.

Рекурсивный алгоритм вычисления чисел Фибоначчи

Если начать упорно считать эти числа, раскладыывая рекурсивную формулу, то получится следующее:
- F(5) = F(4) + F(3)
- F(4) = F(3) + F(2)
- F(3) = F(2) + F(1)
- F(2) = F(1) + F(0)
- F(1) = 1
- F(0) = 0

Так как F(1) = 1 и F(0) = 0, мы можем постепенно вычислить каждое число, начиная с самых маленьких значений:

• F(2) = 1 + 0 = 1
• F(3) = 1 + 1 = 2
• F(4) = 2 + 1 = 3
• F(5) = 3 + 2 = 5

Таким образом, значения чисел Фибоначчи для первых 6 чисел будут выглядеть так:

• F(0) = 0
• F(1) = 1
• F(2) = 1
• F(3) = 2
• F(4) = 3
• F(5) = 5

На этом этапе можно раглядеть рекуррентную формулу следующего вида:

Реализуем её при помощи следующего псевдокода:

    function fn(n) {
    if (n == 0 || n == 1)
        return n

    return fn(n-1) + fn(n-2)
    }

Базовый случай : Если n = 1 или n = 2, вернуть в вызывающую ветку единицу, так как первый и второй элементы ряда Фибоначчи равны единице.
Индуктивный случай: Во всех остальных случаях вызвать эту же функцию с аргументами n - 1 и n - 2. Результат двух вызовов сложить и вернуть в вызывающую ветку программы.

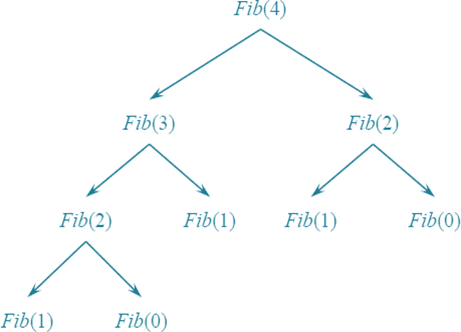
Если начать визуализировать порядок расчетов, то легко увидеть древовидную структуру алгоритма:

Заокономерным вопросом будет: а как же нам посчитать количество операций?

Рекуррентная форма

Рекуррентная формула* (англ. recurrence relation) — это формула вида:

$$a_n = f(n, a_{n-1}, a_{n-2}, \dots, a_{n-p})$$

где:

• $a_n$ — это текущий член последовательности,
• $f(n, a_{n-1}, a_{n-2}, \dots, a_{n-p})$ — функция, которая вычисляет следующий член последовательности на основе предыдущих членов,
• $n$ — номер текущего члена,
• $p$ — порядок рекуррентного соотношения (то есть количество предыдущих членов, которые используются для вычисления следующего).

Рекуррентные формулы часто используются для задания последовательностей, где каждый элемент зависит от одного или нескольких предыдущих элементов. В таких случаях, для нахождения значений последовательности, необходимо знать несколько начальных значений.

Для чисел Фибоначчи рекуррентная формула имеет вид:

/[ F(0) = 0 ]
/[ F(1) = 1 ]
/[ F(n) = F(n-1) + F(n-2) ] для n > 1

Здесь p = 2, так как для вычисления каждого следующего числа нужно использовать два предыдущих.

Дерево рекурсивных вызовов

Дерево рекурсии — это графический метод, который отображает разворачивание рекуррентного соотношения в систему рекурсивных вызовов. В этом дереве каждый узел представляет собой вызов функции, а ветви указывают на рекурсивные вызовы, которые делаются в процессе выполнения алгоритма.

Рассмотрим рекурсивную формулу для чисел Фибоначчи:

/[ F(0) = 0 ]
/[ F(1) = 1 ]
/[ F(n) = F(n-1) + F(n-2) ] для n > 1

Для вычисления, например, F(4), рекурсивные вызовы будут развернуты в дерево следующим образом:

                 F(4)
               /     \
           F(3)      F(2)
         /     \     /     \
     F(2)     F(1) F(1)   F(0)
    /     \
F(1)     F(0)

Здесь:

• Каждый узел представляет вызов функции для конкретного значения /[n].
• Листья дерева показывают базовые случаи /[F(0) = 0] и /[F(1) = 1].

Такое дерево помогает визуализировать, как алгоритм рекурсивно разворачивается и какие промежуточные значения вычисляются.

Визуализация дерева рекурсий

Для лучшего понимания рекурсивных алгоритмов, можно использовать визуальные инструменты, такие как:

• Recursion Tree Visualizer
• Explore and learn algorithms through visualization

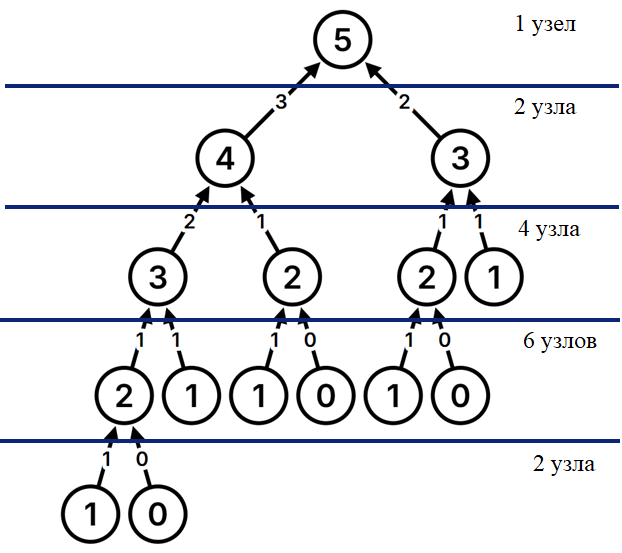
В данном случае, рекурсивные вызовы для чисел Фибоначчи можно представить в виде дерева, где каждый узел — это вызов функции для определенного значения /[n].

Когда будете строить дерево обратите внимание на следующее:
1. Высота дерева зависит от числа вызовов функции и равна /[O(n)], потому что на каждом уровне дерева происходит вычисление для меньших значений /[n] до достижения базовых случаев.
2. На каждом уровне i количество узлов увеличивается в два раза (для каждого вызова функции). То есть на уровне /[i] будет /[2^i] узлов.
3. Каждый узел выполняет определенную работу (в данном случае — вычисление для конкретного значения /[n]), и количество операций, которые нужно выполнить для каждого узла, растет с увеличением /[n]. Для вычисления одного числа Фибоначчи потребуется выполнить около /[2n + 1 - 1] операций.

Анализ рекуррентных соотношений (методом подстановки)

Один из методов анализа алгоритмов — это метод рекуррентных соотношений. Этот метод позволяет вычислять временную сложность рекурсивных алгоритмов на основе их рекуррентных формул. Рассмотрим на примере задачи вычисления чисел Фибоначчи с помощью рекурсии.

Давайте разберем пошагово, чтобы проще было понять.

Шаг 1: Подставляем рекуррентное соотношение для $T(n-1)$

Мы начинаем с рекуррентного соотношения:

$$T(n) = 2 \cdot T(n-1) + 1$$

Теперь подставляем выражение для $T(n-1)$ из предыдущего шага, которое равно:

$$T(n-1) = 2 \cdot T(n-2) + 1$$

Тогда получаем:

$$T(n) = 2 \cdot \left( 2 \cdot T(n-2) + 1 \right) + 1 = 4 \cdot T(n-2) + 3$$

Шаг 2: Подставляем рекуррентное соотношение для $T(n-2)$

Теперь подставим для $T(n-2)$:

$$T(n-2) = 2 \cdot T(n-3) + 1$$

Тогда выражение для $T(n)$ примет вид:

$$T(n) = 2 \cdot \left( 4 \cdot T(n-3) + 3 \right) + 1 = 8 \cdot T(n-3) + 7$$

Шаг 3: Подставляем рекуррентное соотношение для $T(n-3)$

Далее подставим для $T(n-3)$:

$$T(n-3) = 2 \cdot T(n-4) + 1$$

Тогда получаем:

$$T(n) = 2 \cdot \left( 8 \cdot T(n-4) + 7 \right) + 1 = 16 \cdot T(n-4) + 15$$

Шаг 4: Закономерность и общее решение

Из вышеизложенного видно, что на каждом шаге множитель перед $T(n-k)$ удваивается, а добавляемое число увеличивается по закономерности $2^k - 1$.

Таким образом, можно записать общую форму для $T(n)$:

$$T(n) = 2^k \cdot T(n-k) + (2^k - 1)$$

Для любого $k$, где $k$ — это количество шагов рекурсии.

Шаг 5: Определение $k$

Для того чтобы решить это уравнение, нам нужно подставить $T(0) = 1$, то есть:

$$T(0) = 1 \quad \text{при} \quad n-k = 0$$

Следовательно, $k = n$.

Шаг 6: Подставляем $k = n$

Подставляем $k = n$ в общее решение:

$$T(n) = 2^n \cdot T(0) + (2^n - 1) = 2^n + (2^n - 1) = 2^{n+1} - 1$$

Таким образом, мы получаем:

$$T(n) = O(2^n)$$

Для самостоятельного рассмотрения Сложность алгоримта факториал

Естественной мерой объема входных данных для функции factorial является значение $$n$$ . Обозначим через $$T(n)$$ время выполнения программы. Время выполнения строк (1) и (2) имеет порядок O(1), а для строки (3) — O(1) + T(n-1). Таким образом, для некоторых констант $$c$$ и $$d$$ имеем:

• $$T(n) = c + T(n-1)$$ для $$n > 1$$ ,
• $$T(n) = d$$ для $$n ≤ 1$$ .

Полагая, что $$n > 2$$ , и раскрывая в соответствии с рекуррентным соотношением выражение $$T(n-1)$$ (то есть подставляя вместо $$n$$ значение $$n-1$$ ), получаем:

$$T(n) = 2c + T(n-2).$$

Аналогично, если $$n > 3$$ , раскрывая $$T(n-2)$$ , получаем:

$$T(n) = 3c + T(n-3).$$

Продолжая этот процесс, в общем случае для некоторого $$i$$ , где $$n > i$$ , имеем:

$$T(n) = i·c + T(n-i).$$

Положив в последнем выражении $$i = n-1$$ , окончательно получаем:

$$T(n) = c·(n-1) + T(1) = c·(n-1) + d.$$

Из этого следует, что $$T(n)$$ имеет порядок O(n).

---

Рассмотрим теперь другой алгоритм с рекуррентным соотношением:

• $$T(n) = 2T(n/2) + c·n$$ для $$n > 1$$ ,
• $$T(n) = d$$ для $$n = 1$$ .

Заменим в этом соотношении $$n$$ на $$n/2$$ . Получим:

$$T(n/2) ≤ 2T(n/4) + c·(n/2).$$

Подставим это соотношение вместо $$T(n/2)$$ в исходное:

$$T(n) ≤ 2·(2T(n/4) + c·(n/2)) + c·n = 4T(n/4) + 2c·n.$$

Аналогично, заменяя $$n$$ на $$n/4$$ , получаем оценку для $$T(n/4)$$ :

$$T(n/4) ≤ 2T(n/8) + c·(n/4).$$

Подставляя эту оценку в предыдущее неравенство, получаем:

$$T(n) ≤ 8T(n/8) + 3c·n.$$

Индукцией по $$i$$ для любого $$i$$ можно получить следующее соотношение:

$$T(n) ≤ 2^i T(n/2^i) + i·c·n.$$

Предположим, что $$n$$ является степенью числа 2, например, $$n = 2^k$$ . Тогда при $$i = k$$ в правой части неравенства будет стоять $$T(1)$$ :

$$T(n) ≤ 2^k T(1) + k·c·n.$$

Поскольку $$n = 2^k$$ , то $$k = log n$$ . Так как $$T(1) = d$$ , получаем:

$$T(n) ≤ d·n + c·n·log n.$$

Таким образом, $$T(n)$$ имеет порядок роста не более O(n log n).