Введение в асимптотический анализ#

Предисловие#

Согласно Путеводителю для путешествующих по Галактике, сверхразумная раса создала гигантский компьютер Думатель, чтобы тот нашел Окончательный Ответ на величайший вопрос Жизни, Вселенной и Всего Такого. Спустя семь с половиной миллионов лет вычислений он выдал ответ: «Сорок два».

— Сорок два! — воскликнули его создатели. — И это всё, что ты можешь сказать после семи с половиной миллионов лет работы?

— Я всё очень тщательно проверил, — ответил Думатель. — И со всей определённостью заявляю, что это и есть ответ. Проблема в том, что вы сами не знаете, в чём вопрос.

Этот эпизод прекрасно отражает суть программирования и алгоритмизации. Создание программы — это не просто процесс написания кода, а поиск правильной постановки задачи. Часто мы стремимся найти решение, забывая про исходную проблему: что именно мы пытаемся вычислить, спрогнозировать или автоматизировать?

Можно написать сложный алгоритм, который безупречно выполнит расчёты, но если формулировка задачи была неточной или неполной, результат окажется бесполезным — как те самые «сорок два». В программировании важен не только сам процесс написания кода, но и глубокое понимание, что, как и зачем мы автоматизируем.

Алгоритмизация учит нас видеть структуру задач, декомпозировать их на более простые элементы и осознавать, какие данные и операции действительно необходимы. А программирование — это искусство превращения этих идей в работающий код.

В этом курсе вам предстоит столкнуться с методами построения алгоритмов и их реализацией. И, возможно, на первых порах некоторые из них покажутся вам абстрактными, ненужными или даже странными. Однако однажды, решая реальную задачу, вы увидите знакомые элементы и поймёте: ответ уже есть. Вам осталось только правильно задать вопрос.

Понятие алгоритма#

Понятие алгоритма появилось в математике ещё в древности. Долгое время алгоритмы рассматривались как чёткие предписания для решения конкретных задач, и этого было достаточно. Автор предлагал описание своего метода, доказывал его корректность, и этого хватало, чтобы признать результат математически обоснованным.

Но со временем, особенно в алгебре, начали появляться вопросы, относительно которых возникало подозрение: а можно ли вообще найти для них алгоритмическое решение? И если нет, то как это доказать? Для таких случаев потребовалось более строгое и формальное понимание того, что же такое алгоритм.

Прежде чем переходить к точным определениям и различным формализациям, попробуем понять интуитивно: какими свойствами должен обладать любой алгоритм? Интересно, что, несмотря на разные подходы к формализации, все они так или иначе приходят к одному и тому же набору свойств. Это говорит о том, что понятие алгоритма формируется естественным образом, исходя из самой логики вычислений.

Рассмотрим классическую задачу, которая иллюстрирует основные принципы алгоритмического мышления: поиск наибольшего числа в списке.

Представим, что у нас есть набор чисел, и мы хотим найти среди них максимальное. На интуитивном уровне эта задача кажется простой: достаточно последовательно сравнивать элементы и отслеживать наибольшее найденное значение. Давайте формализуем этот процесс в виде алгоритма.

Принять первый элемент списка за временный максимум.
Последовательно просматривать оставшиеся элементы.
Если текущий элемент больше временного максимума — обновить максимум.
По завершении прохода по списку временный максимум и будет наибольшим числом.

Теперь запишем этот алгоритм на псевдокоде:

  Функция НайтиМаксимум(список)
      максимум ← список[0]
      Для каждого числа x в списке, начиная со второго
          Если x > максимум
              максимум ← x
      Вернуть максимум

Анализируя приведённый выше алгоритм поиска максимального числа, можно выделить ключевые характеристики, присущие любому алгоритму.

1 Конечность описания

Любой алгоритм можно записать с помощью конечного набора инструкций. В нашем примере алгоритм поиска максимального числа состоит всего из нескольких шагов, каждый из которых формулируется чётко и лаконично. Это свойство гарантирует, что алгоритм всегда имеет конкретное описание и может быть реализован в виде программы конечного размера.

2 Дискретность

Алгоритм исполняется по шагам, происходящим в дискретном времени. Каждый шаг алгоритма отделён от других, и последовательность его выполнения можно строго зафиксировать. В нашем примере каждый шаг — это обработка одного элемента списка, которая может быть пронумерована.

3 Направленность

Любой алгоритм имеет входные данные, с которыми он начинает работу, и выходные данные, которые он выдаёт по завершении. В случае поиска максимума входом является список чисел, а выходом — найденное максимальное значение. Это свойство делает алгоритм предсказуемым и полезным для решения конкретных задач.

4 Массовость

Алгоритм должен быть применим к целому классу однотипных задач. Он не разрабатывается только под один конкретный случай, а должен работать с различными наборами входных данных. В нашем примере алгоритм поиска максимального числа работает не только с заранее заданным списком, но и с любым списком чисел, независимо от его длины.

5 Детерминированность и конечная недетерминированность

Алгоритм может быть детерминированным (каждый шаг однозначно определён) или конечно недетерминированным (в некоторые моменты допускается несколько вариантов действий, но их число конечно). В нашем примере поиск максимального числа полностью детерминирован: в любой момент выполнения алгоритма точно известно, что делать дальше.

Формализация понятия алгоритма#

Хотя интуитивные свойства алгоритмов дают нам хорошее понимание их структуры, этого недостаточно для строгого математического анализа. Для решения ряда фундаментальных вопросов в теории алгоритмов — например, можно ли в принципе решить ту или иную задачу с помощью вычислений — необходимо строгое формальное определение алгоритма.

В двадцатых годах XX века задача точного определения понятия алгоритма стала одной из центральных математических проблем. Она заключалась в попытке дать строгое математическое определение алгоритма, которое соответствовало бы имевшимся в то время интуитивным представлениям об алгоритме. Решение данной проблемы было получено в первой половине XX века. Мы рассмотрим следующие три варианта определения алгоритма.
1) С точки зрения А.Черча и С. Клини, в алгоритмическом процессе вычисляется значение некоторой функции f x1, x2,...,xn, определенной на множестве натуральных чисел. Строгое определение алгоритма, предложенное Черчем и Клини, основано на понятии частично рекурсивной функции. Они предложили отождествить интуитивное понятие «алгоритм» со строгим математическим понятием «частично рекурсивная функция».
2) С точки зрения английского математика А.Тьюринга алгоритмический процесс — это работа некоторой воображаемой вычислительной машины — машины Тьюринга. Он предложил отождествить интуитивное понятие «алгоритм» с точным понятием «машина Тьюринга». В качестве вычислительной машины будет также рассмотрена машина с неограниченными регистрами (МНР). Это абстрактная машина, более сходная с реальным компьютером по сравнению с машиной Тьюринга.
3) Третий вариант определения алгоритма предложил в 1947 г. российский математик А.А.Марков. С его точки зрения, алгоритмический процесс – это переработка слов некоторого алфавита с помощью точно описанных правил переработки. Вместо интуитивного понятия «алгоритм» А.А.Марков вводит строгое понятие «нормальный алгорифм»
Каждый из трех вариантов определения понятия алгоритма фиксирует свой класс K рассматриваемых объектов, свои правила переработки, окончания и опознания результата. Однако эти три варианта определения понятия алгоритма равносильны. Это означает, что при подходящей кодировке объекты из K можно трактовать в виде объектов, с которыми работают при другом определении алгоритма. То же самое с правилами переработки, правилами окончания и опознания результата. При этом оказывается, что для всех определений и утверждений при одном определении алгоритма возникают аналогичные определения и утверждения при другом определении. Поэтому мы имеем взаимную моделируемость этих понятий. Это указывает на то, что мы открыли некоторую самостоятельную сущность — понятие алгоритма, а три различных определения отражают в разных формах это понятие

Чья идея?	На что похож «алгоритм»	Определение
А. Черч, С. Клини	частично рекурсивная функция	В алгоритмическом процессе вычисляется значение некоторой функции f(x₁, x₂, ..., xₙ), определённой на множестве натуральных чисел.
А. Тьюринг	машина Тьюринга	Алгоритмический процесс — это работа некоторой воображаемой вычислительной машины — машины Тьюринга.
А. А. Марков	нормальный алгоритм	Алгоритмический процесс – это переработка слов некоторого алфавита с помощью точно описанных правил переработки.

Машина Тьюринга#

Алан Тьюринг, работая над проблемой алгоритмической вычислимости, предложил в 1936 году концепцию абстрактной машины, известной как машина Тьюринга.

Основные компоненты машины Тьюринга:
- Лента, разделённая на ячейки, содержащие символы из конечного алфавита.
- Головка, которая может читать символы с ленты, записывать новые символы и перемещаться влево или вправо.
- Конечный набор состояний, определяющих, как машина реагирует на прочитанные символы.
- Таблица переходов, содержащая правила, указывающие, какое действие совершить в зависимости от текущего состояния и символа на ленте.

Тьюринг доказал, что его машина может моделировать работу любого алгоритма, если представить его в виде последовательности элементарных операций. Машины Тьюринга стали одной из фундаментальных моделей вычислений и сыграли важную роль в развитии теории сложности.

Нормальные алгоритмы Маркова#

Советский математик Андрей Марков в 1950-х годах предложил нормальные алгоритмы — формальную модель, основанную на преобразовании строк символов с помощью четко определённых подстановочных правил.

Основные принципы нормальных алгоритмов Маркова:
- Алгоритм представлен в виде набора правил подстановки.
- Вычисления сводятся к последовательному применению этих правил к входному слову.
- Процесс завершается, когда не остаётся применимых подстановок.

Нормальные алгоритмы эквивалентны машинам Тьюринга и $\lambda$ -исчислению, что подтверждает гипотезу Черча — Тьюринга. Они оказались удобными для изучения свойств формальных языков и стали одной из ключевых моделей в теории алгоритмов.

lambda-исчисление Черча#

Вариант строгого определения алгоритма, предложенный Черчем и Клини, рассматривает алгоритмический процесс как процесс вычисления значений некоторой функции $f$ , определённой на множестве натуральных чисел $N$ . Рассмотрим, как это определение формулируется и на чем основано.

Предположим, что имеется некоторый алгоритм, который работает следующим образом:

На вход алгоритма поступает объект $P$ , который представляет собой набор данных $u_1, u_2, \dots, u_n$ , где каждый $u_i$ является словом в некотором алфавите $A$ .
Слова в алфавите $A$ образуют счётное множество, и эти слова могут быть занумерованы натуральными числами.
Таким образом, каждый конструктивный объект $u_i$ имеет номер $x \in \mathbb{N}$ , где $x$ — это натуральное число, которое используется для идентификации объекта.

В данном контексте предполагается, что алгоритм выполняет вычисления, результатом которых является некоторое значение функции $f$ , определённой на множестве натуральных чисел $\mathbb{N}$ . Функция $f$ представляет собой отображение, которое, в общем случае, может быть определено не для всех входных данных.

Tip

Когда имеется некоторый объект $P$ на входе алгоритма, это вовсе не означает, что алгоритм всегда приводит к некоторому объекту $Q$ на выходе. В некоторых случаях алгоритм может не иметь результата, что делает вычисление функции $f$ неопределённым для определённых наборов данных.
В связи с этим возникает понятие частичной функции. Частичная функция — это такая функция, которая может быть определена только для подмножества входных данных. Например, алгоритм может правильно обработать один набор входных данных и не дать результата для другого.

Частичная функция играет ключевую роль в контексте алгоритмов, поскольку:

Алгоритм не всегда имеет гарантированный результат для всех возможных входных данных.
Для некоторых наборов данных алгоритм может не завершиться или не выдать корректного результата.

Таким образом, несмотря на то, что алгоритм представляет собой конечную последовательность операций, его поведение может зависеть от конкретных входных данных, что и ведёт к необходимости использования частичных функций.

Теорема о рекурсии#

Рассмотрим произвольную вычислимую функцию от двух аргументов $V(x, y)$ . Теорема о рекурсии утверждает, что всегда можно найти эквивалентную этой функции $p(y) = V(p, y)$ , которая будет использовать саму себя для вычисления значения.

Tip

Пусть — вычислимая функция. Тогда найдется такая вычислимая функция , что для всех :
$p(y) = V(p, y)$

Доказательство

Приведем конструктивное доказательство теоремы.

Введем новые обозначения для псевдокода. Внутри блока program располагаются функции, среди которых есть функция main:

  program int p(int x):
  ...

  int main():
    ...

 ...

Тогда вызов p(x) — вызов функции main от соответствующего аргумента.

Все входные данные далее можно интерпретировать как строки, поэтому все типы аргументов и возвращаемых значений будут иметь тип string. Пусть есть вычислимая V(x, y). Будем поэтапно строить функцию p(y).

Предположим, что у нас в распоряжении есть функция getSrc(), которая вернет код p(y). Тогда саму p(y) можно переписать так:

string p(string y): 
  string V(string x, string y):
    ...

  string main():
    return V(getSrc(), y)

  string getSrc():
    ...

Теперь нужно определить функцию getSrc(). Предположим, что внутри p(y) мы можем определить функцию getOtherSrc(), состоящую из одного оператора return, которая вернет весь предшествующий ей код. Тогда p(y) перепишется так:

string p(string y): 
  string V(string x, string y):
    ...

  string main():
    return V(getSrc(), y)

  string getSrc():
    string src = getOtherSrc()
    return ```$src                    // символ $ перед названием переменной используется для подстановки значения этой переменной в строку
             |string getOtherSrc():   // многострочные строки заключаются в ``` и используют | в качестве разделителя
             |    return $src```

  string getOtherSrc():
    ...

Теперь getOtherSrc() определяется очевидным образом, и мы получаем итоговую версию функции p(y):

string p(string y): 
  string V(string x, string y):
    ...

  string main():
    return V(getSrc(), y)

  string getSrc():
    string src = getOtherSrc()
    return ```$src 
             |string getOtherSrc(): 
             |    return $src```

  string getOtherSrc():
    return ```function  p(int y):       
             |  int V(string x, int y):
             |    ...
             |
             |  int main():
             |    return V(getSrc(), y)
             |
             |  string getSrc():
             |    string src = getOtherSrc()
             |    return \```$src 
             |              |string getOtherSrc(): 
             |              |   return \$src\

Иначе говоря, если рассмотреть V(x, y), как программу, использующую x в качестве исходного кода и выполняющую действие над y, то теорема о рекурсии показывает, что мы можем написать эквивалентную ей программу p(y) = V(p, y), которая будет использовать собственный исходный код.

Тезис Черча#

Тезис Черча

Каждая вычислимая функция частично рекурсивна.

Итак, мы располагаем некоторым запасом вычислимых функций, а именно частично рекурсивными функциями. Обозначим множество всех вычислимых функций через A, а множество всех частично рекурсивных функций через B. Так как всякая частично рекурсивная функция является вычислимой функцией, то B A, что отражает следующий рисунок

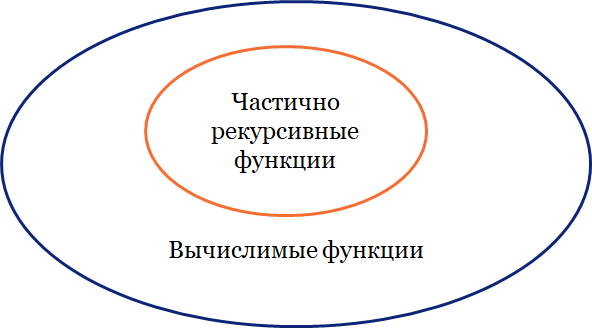
Сможем ли мы доказать тезис Черча? Нет, поскольку у нас нет точного определения вычислимой функции. Тезис Черча — это просто строгое определение алгоритма. Это положение является соглашением, возникшим в результате длительного исследования интуитивного понятия алгоритма.

Показана рекурсивность огромного количества вычислимых функций. Никто не сумел построить вычислимую функцию, рекурсивность которой нельзя было бы доказать, или хотя бы указать правдоподобный метод построения такой функции.

Тезис Черча является естественнонаучным фактом, который подтверждается опытом, накопленным математикой за весь период её развития. Тезис Черча является достаточным средством, чтобы придать необходимую точность формулировкам алгоритмических проблем и делает возможным доказательство их неразрешимости.

Заметим, что Черч рассматривал лишь всюду определенные вычислимые функции. С. Клини ввел понятие частично рекурсивной функции и высказал гипотезу, что все частичные функции, вычислимые посредством алгоритма, являются частично рекурсивными. Мы не будем различать тезисы Черча и Клини и под тезисом Черча понимаем более общую формулировку.

Как оценить работу алгоритма?#

Тезис Черча в явном виде приводит нас к мысли, что алгоритм и функция, пускай и с некоторыми ограничениями, весьма похожи по своему поведению. Если это так, то весь математический аппарат анализа поведений функций применим и к алгоритмам. Ключевым вопросом для любой функции является какими переменными она оперирует.

Из практики алгоритмизации выделяют следующие переменные:
1. Машинное (процессное) время (Т) – это время, которое требуется алгоритму для решения задачи. Время работы зависит от сложности алгоритма и размера входных данных.
2. Оперативная память (М) – объём памяти, необходимый алгоритму для хранения данных в процессе вычислений. Эффективное использование памяти имеет большое значение при работе с большими объёмами данных.
3. Долговременная память – пространство на жестком диске, которое используется для хранения данных, не помещающихся в оперативную память. Это может быть критично для обработки больших наборов данных или при ограничениях по памяти.
4. Пропускная способность сети (трафик) – необходимая для обмена данными между компонентами системы (например, при распределённых вычислениях или при необходимости передачи данных по сети).
5. Энергия – энергия, которая поглощается вычислительным процессом и выделяется в окружающую среду. Это может быть важно для систем с ограниченной энергетической мощностью, например, для мобильных устройств.
6. Другие ресурсы – в зависимости от контекста могут быть другие типы ресурсов, такие как время ввода/вывода, использование графических процессоров и так далее.

Tip

Часто удается сократить потребление одного ресурса за счет увеличения потребления другого. Например, можно уменьшить время работы алгоритма за счёт увеличения объема памяти, используемой системой. Такое компромиссное использование ресурсов помогает оптимизировать работу алгоритма в реальных условиях.

Абстрактная модель вычислений#

Поскольку мы работаем с абстрактными алгоритмами, то следует зафиксировать некоторые набор утверждений

Алгоритм рассматривается как набор операций и управляющих структур. Каждая операция выполняет определённое действие, которое занимает некоторое время, а управляющие структуры (например, циклы, условия) определяют, как именно выполняются операции.
Каждому виду операций сопоставляется временная стоимость. Стоимость операции измеряется в абстрактных единицах времени (шага), которые учитываются при оценке времени работы алгоритма.
Время работы алгоритма в целом равно сумме стоимостей составляющих его операций с учётом вложенности управляющих структур. Это означает, что для точной оценки необходимо учитывать не только время, которое тратится на отдельные операции, но и то, как они расположены внутри других операций (например, сколько раз выполняется вложенный цикл).

Note

Время работы алгоритма в целом равно сумме стоимостей составляющих его операций с учетом вложенности управляющих структур

№	Управляющая структура	Запись на языке Pascal	Вычислительная сложность структуры
1	Составной оператор	`begin` `S1;` `S2;` `…` `end;`	T = ∑T(Si)
2	Цикл	`for i := 1 to N do S;` `While U do S;` `Repeat S; Until U;`	T = N * T(S), где N – число итераций цикла
3	Условие	`if U then S1` `else S2;`	T = T(U) + iT(S1), если U T(S), иначе

Асимптотический анализ#

Расчёт значений с точными коэффициентами является сложным, а иногда и невозможным. В этом случае удобно абстрагироваться от некоторых деталей. Допустим, что для некоторого алгоритма среднее время работы можно выразить полиномом второй степени. Несомненно было бы удобно упростить его, чтобы:

не учитывать информацию, которая несильно влияет на итоговую формулу,
легко было оценивать время работы,
легко было сравнивать алгоритмы между собой.
Для этого можно использовать вместо точной оценки временной сложности её асимптотическую оценку, которая может быть выражена одной из 3 греческих букв:

Θ(g(n)) — асимптотически точная граница. Тогда для такой функции g(n) это обозначение будет означать множество таких функций, что:

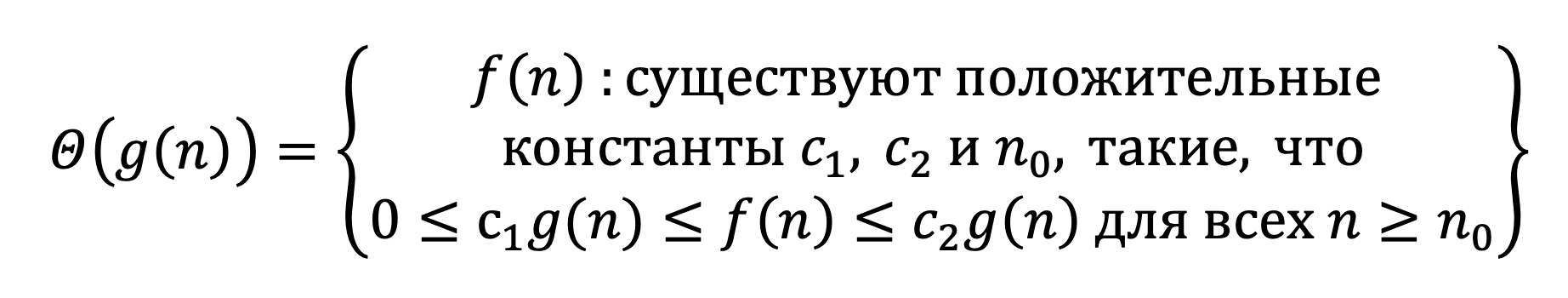
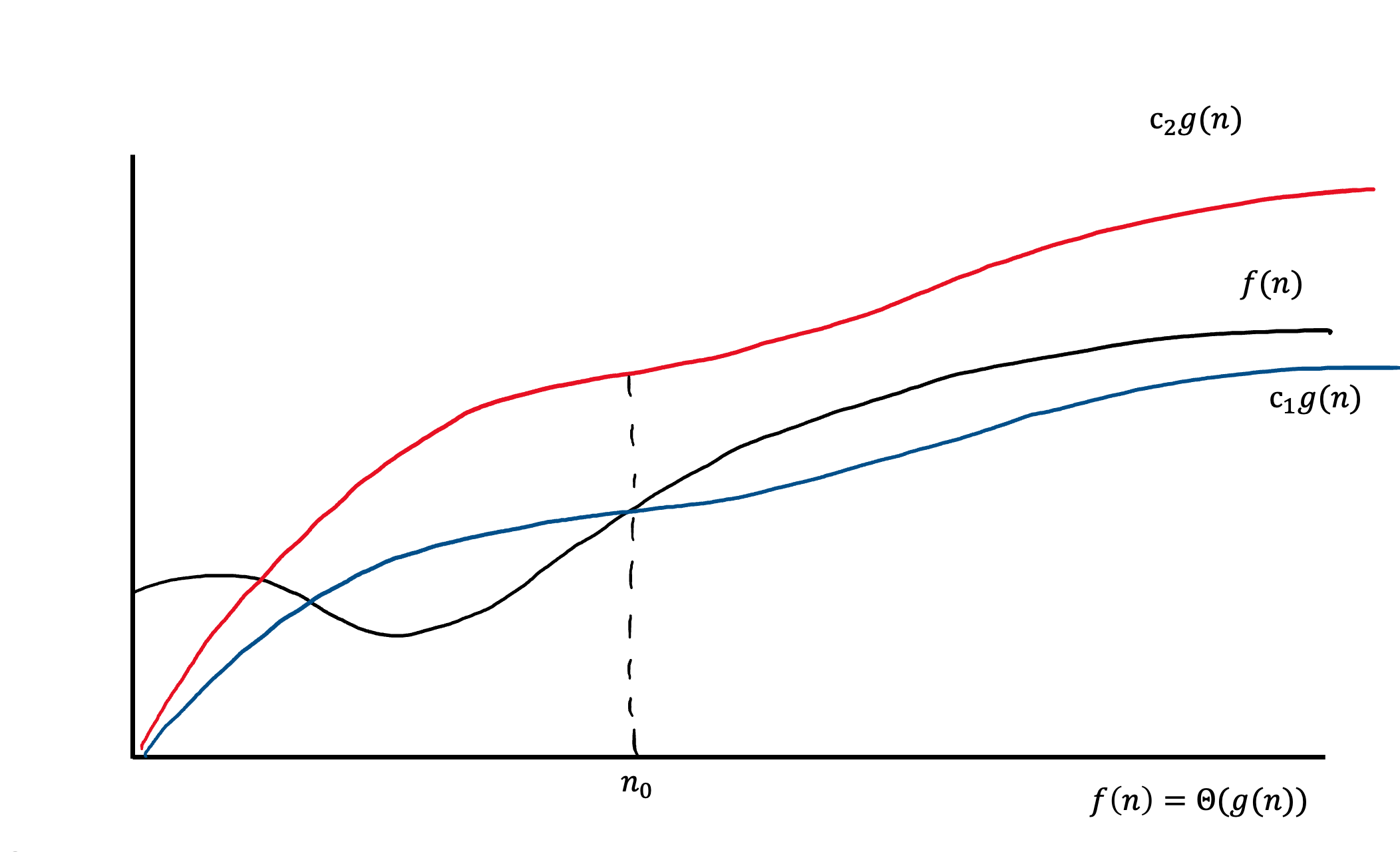
Другими словами, эту оценку можно применять ко всем функциям, которые оказываются стиснутыми между красным и синем графиками. На изображении видно, что эти графики являются одной и той же функцией, взятой с разным коэффициентом. Также, эти функции могут вести себя иначе до некоторого значения n_0.

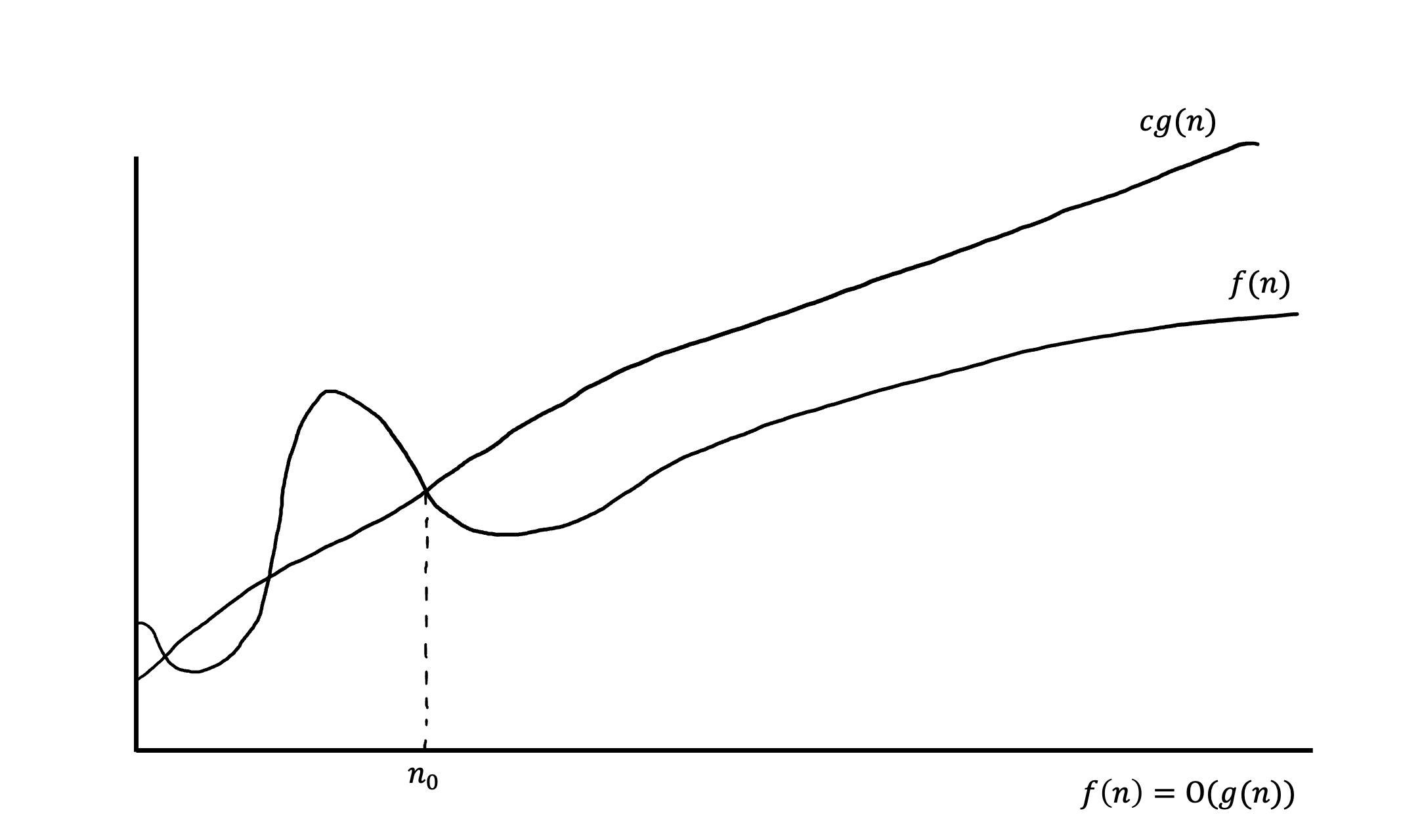
Ο(g(n)) — асимптотически верхняя граница, для которой все функции будут находиться ниже. Более формально:

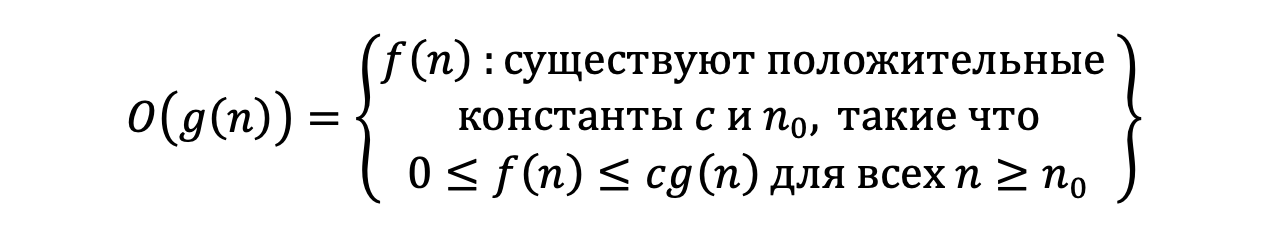
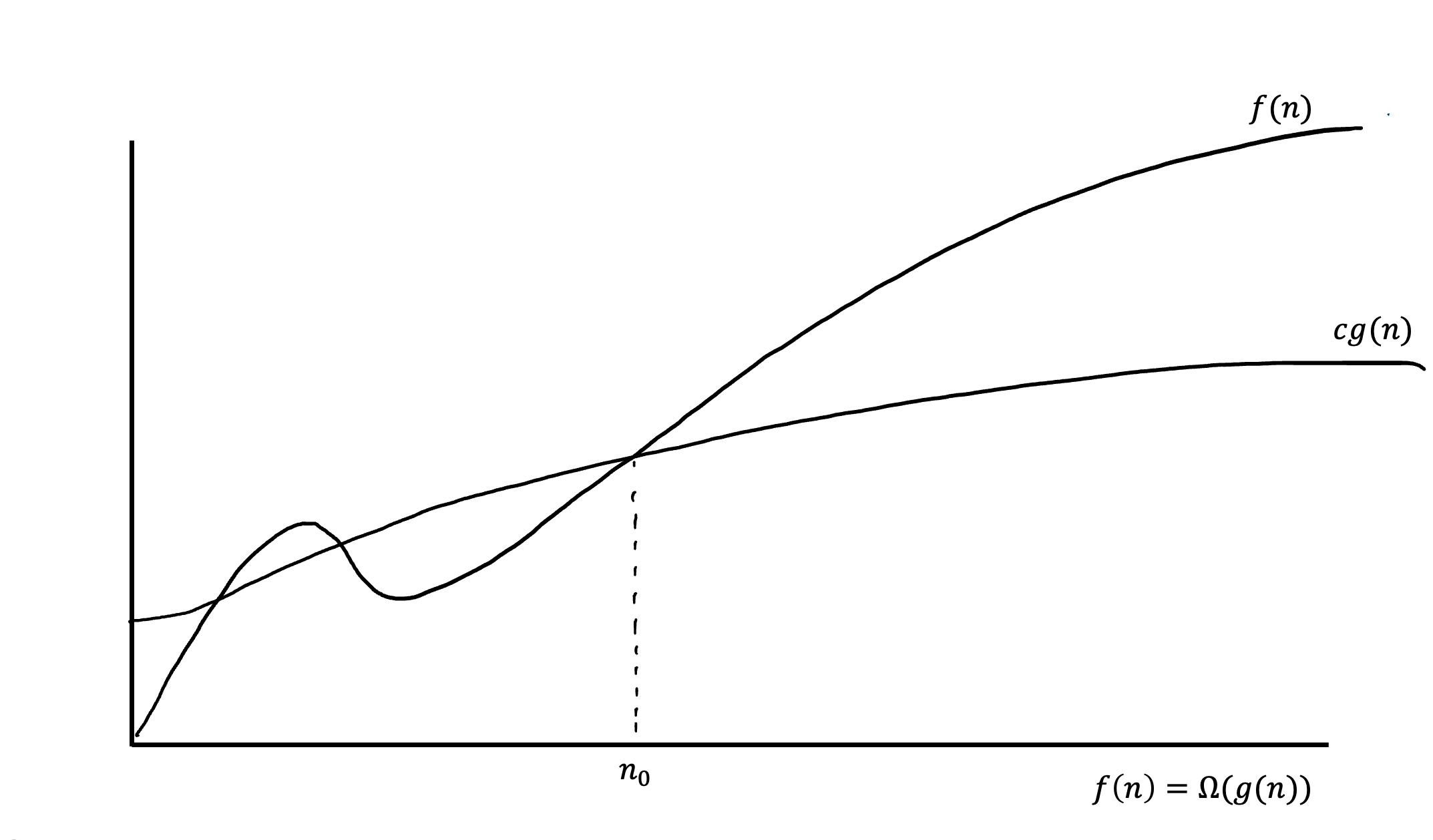
Ω(g(n)) — асимптотически нижняя граница, для которой все функции будут находиться выше. Или опять же более формально:

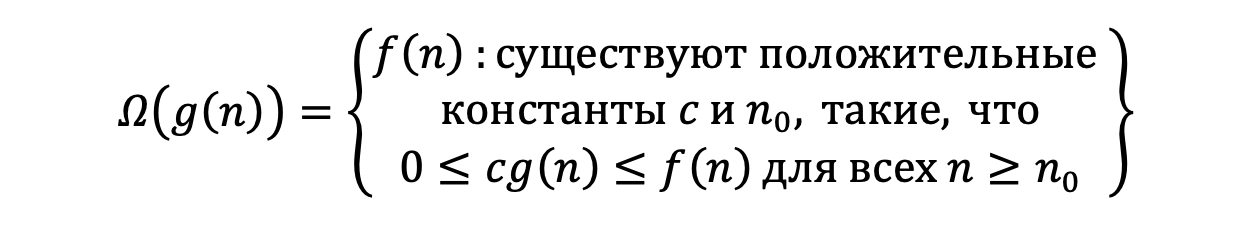
Приведем таблицу "типичных" функций, которые могут быть получены в ходе анализа алгоритма

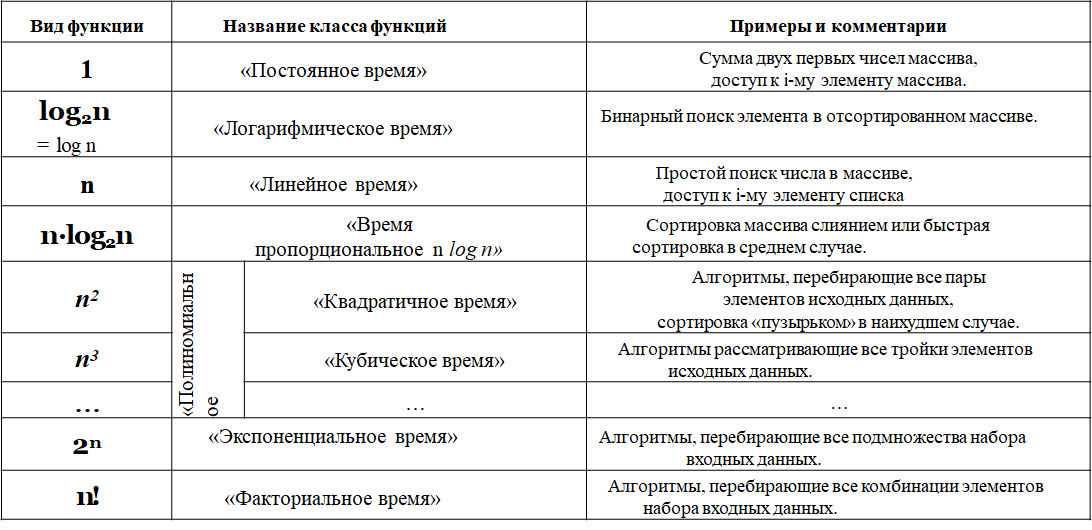
Оценка работы рекурсивных алгоритмов#

Рекурсивными являют такие алгоритмы, которые в ходе работы могут вызывать сами себя с другими аргументами. Обычно, размер данных для обработки при этом уменьшается. Это свойство лежит в основе концепции «Разделяй и властвуй». Для них в алгоритме можно выделить 3 основных шага:

Разделение задачи на несколько подзадач, которые представляют собой меньшие экземпляры той же задачи.
Обработка подзадач путём их рекурсивного решения. Если размеры подзадач малы, то такие подзадачи решаются непосредственно.
Комбинирование подзадач в решение исходной задачи.

Возьмём для примера работу двоичного поиска. Здесь время работы будет константным, если n = 1, либо суммой времени работы подзадачи и собственными задачами. В задаче двоичного поиска к собственным задачам относятся, например, получение элемента по нужному индексу, сравнение его с искомым элементом, определение, какую из двух половин выбрать для дальнейшего поиска. Подзадача же на каждом шаге уменьшается вдвое. Всё это можно выразить в виде рекуррентного соотношения.

Существуют разные методы для определения общего времени работы рекурсивных алгоритмов, например:

Метод подстановки
Мастер-теорема

Метод подстановки#

Суть метода подстановки заключается в попытке «догадаться», как будет выглядеть оценка функции, после чего методом индукции проверить её на правильность.

Покажем это для двоичного поиска, для которого известно, что $T(n) = T\left(\frac{n}{2}\right) + \Theta(1)$ .

Сначала докажем, что в индукции срабатывает переход от предыдущего значения к следующему. Допустим, что $T(n) = O(\log_2 n)$ . Тогда необходимо показать, что $T(n) \le c \log_2 n$ для правильно подобранного значения $c > 0$ .

Предположим, что это ограничение уже верно для всех значений $m < n$ . Например, для $m = \frac{n}{2}$ , тогда

$T\left(\frac{n}{2}\right) \le c \log_2 \frac{n}{2}$

Подставляя в исходное рекуррентное соотношение получаем:

$T(n) = T\left(\frac{n}{2}\right) + \Theta(1) \le c \log_2 \frac{n}{2} + d = c \log_2 n - c + d \le c \log_2 n$

Последнее неравенство выполняется при $c \ge 1$ и $d \le c$ . А значит шаг индукции доказан.

Теперь необходимо найти базис индукции. Поскольку $T(1) = d$ , а $c \log_2 1 = 0$ для любого $c$ , выражение $T(1) \le c \log_2 1$ не является истиной и не может быть базой, если $d > 0$ . Воспользуемся тем, что для асимптотических оценок достаточно найти $n_0$ , при котором соотношение становится верным:

$T(1) = d, \quad c \log_2 1 = 0 \quad \Rightarrow \quad d \le 0$

$T(2) = 2d, \quad c \log_2 2 = c \quad \Rightarrow \quad 2d \le c$

$T(4) = 3d, \quad c \log_2 4 = 2c \quad \Rightarrow \quad 3d \le 2c$

Возьмем базис при $n_0 = 2$ , тогда при $c = 2d$ индукция будет доказана.

Мастер-теорема#

Самым простым методом определения времени работы считается использование мастер-теоремы. Суть которой в том, что рекуррентное соотношение можно представить в общем виде как:

$T(n) = aT\left(\frac{n}{b}\right) + f(n)$

где $a \geq 1$ , $b > 1$ , а $f(n)$ — заданная функция. Здесь $a$ означает количество подзадач, на которое делится исходная подзадача, а $b$ — во сколько раз уменьшается количество данных при вызове рекурсивной функции. $f(n)$ — это работа по обработке 1 вызова метода рекурсии. Далее ответ зависит от одного из трёх случаев, с помощью которого асимптотические оценки определяются достаточно просто:

Если $f(n) = O\left(n^{\log_b a - \epsilon}\right)$ для некоторого $\epsilon > 0$ , то $T(n) = \Theta\left(n^{\log_b a}\right)$
Если $f(n) = \Theta\left(n^{\log_b a}\right)$ , то $T(n) = \Theta\left(n^{\log_b a} \log_2 n\right)$
Если $f(n) = \Omega\left(n^{\log_b a + \epsilon}\right)$ для некоторого $\epsilon > 0$ и если $a f\left(\frac{n}{b}\right) \leq c f(n)$ для некоторой $c < 1$ , то $T(n) = \Theta(f(n))$

Рассмотрим её применение для двоичного поиска:

$T(n) = T\left(\frac{n}{2}\right) + d$

Поскольку $d = \Theta\left(n^{\log_2 1}\right) = \Theta(n^0) = \Theta(1)$ , то срабатывает второе правило мастер-теоремы, и ответом является:

$T(n) = \Theta\left(n^{\log_2 1} \log_2 n\right) = \Theta(\log_2 n)$

Рассмотрим другой пример, рассмотренный ранее. Пусть:

$T(n) = 4T\left(\frac{n}{2}\right) + kn$

Попробуем применить 3-е правило мастер-теоремы, где $a = 4$ , $b = 2$ , и проверить утверждение, что: $f(n) = \Omega\left(n^{\log_2 4 + \epsilon}\right)$ . Но, поскольку функция $kn$ не может быть оценена снизу, т.е. $kn \neq \Omega\left(n^{\log_2 4 + \epsilon}\right)$ для любого $\epsilon > 0$ , то это правило не может быть применено.

Попробуем применить 2-е правило мастер-теоремы, тогда: $f(n) = \Theta\left(n^{\log_2 4}\right)$ , но и в этом случае оно не работает, т.к. $kn \neq \Theta(n^2)$ .

Рассмотрим первое правило: $f(n) = O\left(n^{\log_2 4 - \epsilon}\right)$ . В этом случае $kn = O\left(n^{2 - \epsilon}\right)$ при $0 < \epsilon \leq 1$ . Тогда $T(n) = \Theta\left(n^{\log_b a}\right) = \Theta(n^2)$ .

Неразрешимые задачи за пределами теории алгоритмов#

В этой лекции мы дали определение алгоритма, узнали, как исходя из определения, производить оценку алгоритмов, однако открытым остался вопрос Что не решается алгоритмически?

На самом деле Многие задачи, несмотря на свою кажущуюся простоту, не имеют алгоритмического решения, то есть нет общего метода, который бы позволял решить эти задачи за конечное время, используя конечные ресурсы. Эти задачи выходят за пределы теории алгоритмов, потому что они принадлежат к классу неразрешимых или нерешаемых задач.

Теорема Геделя о неполноте#

Одной из самых влиятельных теорем в области теории вычислений и логики является Теорема Гёделя о неполноте. Теорема Гёделя, сформулированная Куртом Гёделем в 1931 году, устанавливает важные пределы в математической логике и вычислениях, что связано с понятием разрешимости.

Формулировка Теоремы Гёделя о неполноте

Первая теорема о неполноте: В любой достаточно мощной формальной системе, которая включает арифметику натуральных чисел, существуют утверждения, которые не могут быть доказаны или опровергнуты в рамках этой системы. То есть система не является полной.
Вторая теорема о неполноте: Если система непротиворечива, то она не может доказать свою собственную непротиворечивость. Это означает, что невозможно внутри формальной системы доказать, что система сама по себе не содержит противоречий.

Курт Гёдель придумал очень изящный способ доказательства своей теоремы о неполноте, который можно объяснить без глубоких математических деталей, используя метафору с карточками.

Представьте, что вы собираете систему карточек, каждая из которых представляет собой утверждение или утверждение, которое можно доказать в некоторой логической системе (например, в арифметике). Каждая карточка может быть как истинной, так и ложной. Ваша цель — построить систему, в которой вы можете оценить, какие утверждения могут быть доказаны или опровергнуты.

Теперь представьте, что у вас есть несколько правил, как именно эти карточки могут быть связаны друг с другом. Это и есть логическая система, такая как арифметика или теория чисел. Все карточки, которые подчиняются этим правилам, могут быть либо доказаны, либо опровергнуты, если вы следуете правильным логическим шагам.

Гёдель в своей теореме, на самом деле, создал систему, где на каждой карточке было написано не просто утверждение, а более сложная конструкция, которая касалась самой системы карточек. Это можно представить как карточку, на которой написано: "Эту карточку нельзя доказать". Эта конструкция была ключом к доказательству Гёделя.

Он применил технику, которая сейчас называется самореференцией — это когда утверждение делает ссылку на себя. Карточка, которую он создал, становится своего рода логической ловушкой. Если бы мы могли доказать её истинность, это означало бы, что она ложна (так как она говорит, что не может быть доказана), и наоборот, если бы мы могли доказать, что она ложна, это бы подтверждало её истинность. Таким образом, это утверждение нельзя было ни доказать, ни опровергнуть в пределах самой системы.

Через это Гёдель показал, что в любой достаточно мощной формальной системе существуют утверждения, которые не могут быть доказаны или опровергнуты с использованием самой этой системы — они являются неразрешимыми.

Этот подход оказался революционным, потому что он продемонстрировал, что для любой такой системы существуют задачи, которые выходят за её пределы и не могут быть решены её средствами. Гёдель доказал, что системы, способные описывать базовые арифметические операции, неполны, потому что они не могут доказать все истинные утверждения о натуральных числах, например.

Таким образом, Гёдель не просто показал, что теорема невозможна для доказательства — он создал логическую конструкцию, которая сама по себе делает невозможным доказательство в рамках той же системы.

Проблема замощения плитки Вана#

Плитки Вана (или домино Вана), впервые предложенные математиком, логиком и философом Хао Ваном в 1961, — это класс формальных систем. Они моделируются визуально с помощью квадратных плиток с раскрашиванием каждой стороны. Определяется набор таких плиток (например, как на иллюстрации), затем копии этих плиток прикладываются друг к другу с условием согласования цветов сторон, но без вращения или симметрического отражения плиток.

Основной вопрос о наборе плиток Вана — могут ли они замостить плоскость или нет, то есть может ли плоскость быть заполнена таким способом. Следующий вопрос, может ли она быть заполнена в виде периодического узора.

Для вас подготовлена следующая иллюстрация, помогающая понять суть проблемы

Задача усердного бобра#

Задача усердного бобра (или задача о бобре) (англ. busy beaver) — это классическая неразрешимая задача в теории вычислений, которая связана с вычислением максимального числа шагов, которое может выполнить машина Тьюринга до того, как она остановится, при условии, что эта машина начинает в пустом состоянии и на входе нет данных.

Задача заключается в следующем: мы имеем машину Тьюринга с конечным числом состояний, которая выполняет простую задачу — она находит максимально возможное количество шагов, которые может сделать эта машина до того, как она остановится. Условия задачи следующие:

Машина Тьюринга начинается в пустом состоянии.
Она работает на пустой ленте, которая инициализируется нулями.
Машина должна остановиться, то есть прекратить вычисления после выполнения определённого количества шагов.

Задача состоит в том, чтобы найти максимальное количество шагов, которые может сделать машина Тьюринга с заданным количеством состояний, прежде чем она остановится. Этот максимальный результат и называется числом усердного бобра для заданного числа состояний.

Предположим, что мы рассматриваем машину Тьюринга с двумя состояниями (обозначим их S1 и S2). Если мы знаем алгоритм, который при этом количестве состояний останавливается после 10 шагов, то число усердного бобра для этой машины будет равно 10. Но можно ли предсказать это число для произвольного количества состояний?

Число растёт очень быстро. Задача усердного бобра — это не просто математическая загадка. Она растёт экспоненциально и даже быстрее. Уже для маленьких чисел состояний это число может быть очень большим и трудно вычисляемым.
Неразрешимость. Проблема усердного бобра связана с теоремой о неразрешимости задачи. Для любого количества состояний, большее или равное четырём, невозможно точно вычислить число усердного бобра. Это связано с тем, что задача требует анализа всех возможных конфигураций машины Тьюринга, и количество возможных конфигураций растёт очень быстро.

Задача усердного бобра демонстрирует, что существуют задачи, которые невозможно решить с помощью алгоритмов. Она помогает понять границы вычислимости и связь с такими важными концепциями, как остановка программы (проблема остановки). Эта задача стала классическим примером для исследования неразрешимых проблем в вычислениях.

Суть её заключается в том, что даже в хорошо определённых и казалось бы ограниченных системах, таких как машины Тьюринга с фиксированным количеством состояний, мы всё равно сталкиваемся с невозможностью предсказать их поведение для всех входных данных.